一 : 工程流体力学
题号:861
《工程流体力学》
考试大纲
一、 考试内容
根据学校教学及该试题涵盖专业的特点,对考试范围作以下要求:
1.流体的基本特性:流体的分子特点与力学特性,流体的压缩性、膨胀性、粘性及热传导性的概念,及其物理本质及影响因素。
(www.61k.com。2.流体静力学:静止流体受力及其计算方法;流体静力学平衡方程及其应用;非惯性坐标系中静止流体平衡方程的应用;静止流体内部压强计算方法;压强测量方法。
3.一维定常流动:迹线、流线、流管的概念;流线方程、迹线方程;一维定常流动的连续方程、动量方程、能量方程和伯努力方程的物理意义及其应用。
4.管道流动:完全发展的管道层流和湍流流动;管道流动损失的分类,产生的原因;流动损失计算方法;串、并联及分支管道流动损失的计算原则和方法。
5.流体多维运动:多维流动中随流导数的概念和计算方法;多维流运动分析及变形量计算;多维流的连续性方程、动量方程和能量方程及其边界条件。
6.不可压平面势流:流函数、势函数概念及其与速度之间的关系;直匀流,点源,点涡,偶极子的流函数和势函数;叠加原理及其应用;圆柱绕流及特点。
7.粘性流动:粘性应力和广义牛顿定律;粘性流体运动方程;边界层概念及其特点;边界层厚度及积分关系式应用;分离现象及物理本质。
8.可压缩平面流动:可压缩流体的压强、温度、密度、马赫数等概念及反映相互关系的气动函数的应用。
9.扰动波在气流中的传播规律;膨胀波和激波的概念和计算。
10. 可压缩一维定常流动:可压缩一维管流的方程及计算方法;换热管流计算;收敛喷管和拉瓦尔喷管流动状态及计算。
二、 参考书目
1.邢宗文主编:《流体力学基础》,西北工业大学出版社,1992。
2.王新月主编:《气体动力学基础》,西北工业大学出版社,2006。
3.王新月主编:《热力学与气体动力学基础》,西北工业大学出版社,2004。
4.张也影主编:《流体力学》(第二版),高等教育出版社,1999。
原文地址.html
题号:861《工程流体力学》
考试大纲
一、 考试内容
根据学校教学及该试题涵盖专业的特点,对考试范围作以下要求:
1.流体的基本特性:流体的分子特点与力学特性,流体的压缩性、膨胀性、粘性及热传导性的概念,及其物理本质及影响因素。
2.流体静力学:静止流体受力及其计算方法;流体静力学平衡方程及其应用;非惯性坐标系中静止流体平衡方程的应用;静止流体内部压强计算方法;压强测量方法。
3.一维定常流动:迹线、流线、流管的概念;流线方程、迹线方程;一维定常流动的连续方程、动量方程、能量方程和伯努力方程的物理意义及其应用。
4.管道流动:完全发展的管道层流和湍流流动;管道流动损失的分类,产生的原因;流动损失计算方法;串、并联及分支管道流动损失的计算原则和方法。
5.流体多维运动:多维流动中随流导数的概念和计算方法;多维流运动分析及变形量计算;多维流的连续性方程、动量方程和能量方程及其边界条件。
6.不可压平面势流:流函数、势函数概念及其与速度之间的关系;直匀流,点源,点涡,偶极子的流函数和势函数;叠加原理及其应用;圆柱绕流及特点。
7.粘性流动:粘性应力和广义牛顿定律;粘性流体运动方程;边界层概念及其特点;边界层厚度及积分关系式应用;分离现象及物理本质。
8.可压缩平面流动:可压缩流体的压强、温度、密度、马赫数等概念及反映相互关系的气动函数的应用。
9.扰动波在气流中的传播规律;膨胀波和激波的概念和计算。
10. 可压缩一维定常流动:可压缩一维管流的方程及计算方法;换热管流计算;收敛喷管和拉瓦尔喷管流动状态及计算。
二、 参考书目
1.邢宗文主编:《流体力学基础》,西北工业大学出版社,1992。
2.王新月主编:《气体动力学基础》,西北工业大学出版社,2006。
3.王新月主编:《热力学与气体动力学基础》,西北工业大学出版社,2004。
4.张也影主编:《流体力学》(第二版),高等教育出版社,1999。
西南交通大学200 -200 学年第( )学期考试试卷
班 级 学 号 姓 名
课程代码 013**** 课程名称 工程流体力学A 考试时间 120 分钟 密封装订线 密封装订线
阅卷教师签字:
(本大题共15小题,每小题1分,共15分)在每小题列出的四个备选项中
只有一个是符合题目要求的,请将其代码填写在题后的括号内。错选、多选或未选均无分。
1.交通土建工程施工中的新拌建筑砂浆属于( )
A、牛顿流体 B、非牛顿流体 C、理想流体 D、无黏流体
2.牛顿内摩擦定律
dudu中的为运动流体的( )
dydy
A、拉伸变形 B、压缩变形 C、剪切变形 D、剪切变形速率
3.平衡流体的等压面方程为( )
A、fxfyfz0 B、fxfyfz0 C、fxdxfydyfzdz0 D、fxdxfydyfzdz0 4.金属测压计的读数为( )
A、绝对压强p B、相对压强p C、真空压强pv D、当地大气压pa 5.水力最优梯形断面渠道的水力半径R( ) A、h/4 B、h/3 C、h/2 D、h 6.圆柱形外管嘴的正常工作条件是( )
A、l(3~4)d,H09m B、l(3~4)d,H09m C、l(3~4)d,H09m D、l(3~4)d,H09m 7.完全潜水井的产水量Q与( )
A、渗流系数k成正比 B、井的半径r0成正比 C、含水层厚度H成正比 D、影响半径R成正比 8.理想流体的切应力( )。
A、 0 B、
dudu2du22du2
C、 l() D、+l()
dydydydy
9.在工程流体力学中,常取的基本量纲为( )
A、质量量纲M、长度量纲L、时间量纲T B、流量量纲Q、长度量纲L、时间量纲T C、压强量纲P、长度量纲L、时间量纲T D、压力量纲P、长度量纲L、温度量纲T
10.静止液体作用在曲面上的静水总压力的水平分力PxpcAxghcAx,式中的( )
A、pc为受压面形心处的绝对压强 B、pc为压力中心处的相对压强 C、Ax为受压曲面的面积 D、Ax为受压曲面在铅垂面上的投影面积 11.圆管紊流运动的断面流速分布为( )
A、平面 B、抛物面 C、双曲面 D、对数曲面 12.从本质上讲,紊流应属于( )
A、恒定流 B、非恒定流 C、均匀流 D、恒定非均匀流 13.工程流体力学中描述流体运动的方法一般采用( )
A、欧拉法 B、普兰特法 C、拉格朗日法 D、尼古拉兹法
14.已知不可压缩流体的流速场为uxf(y,z),uyf(x),uz0,则该流动属于( )
A、一元流 B、二元流 C、三元流 D、非恒定流 15.理想流体是指( )
A、忽略密度变化的流体 B、忽略温度变化的流体 C、忽略黏性变化的流体 D、忽略黏性的流体
二、多项选择题(本大题共5小题,每小题2分,共10分)在每小题列出的五个备选项中
至少有两个是符合题目要求的,请将其代码填写在题后的括号内。错选、多选、少选或未选均无分。
16.1个工程大气压=( )
A、98kPa B、10mH2O C、1.0kgf/cm D、760mmHg E、101.3kPa 17.下列关于长管水力计算的说法中,正确的有( ) A、串联管路的总水头损失等于各支路的水头损失之和 B、串联管路的总流量等于各支路的流量之和
C、并联管路两节点间的总水头损失等于各支路的水头损失 D、并联管路各支路的水头损失相等
E、并联管路两节点间的总流量等于各支路的流量之和 18.下列关于压力体的说法中,正确的有( )
A、当压力体和液体在曲面的同侧时,为实压力体,Pz B、当压力体和液体在曲面的同侧时,为虚压力体,Pz
2
C、当压力体和液体在曲面的异侧时,为实压力体,Pz D、当压力体和液体在曲面的异侧时,为虚压力体,Pz E、当压力体和液体在曲面的异侧时,为虚压力体,Pz
19.水在土壤中存在的形式主要有( )
A、气态水 B、重力水 C、毛细水 D、薄膜水 E、吸附水 20.下列关于水流流向的说法中,不正确的有( )。 A、水一定是从高处向低处流 B、水一定是从流速大处向流速小处流 C、水一定是从压强大处向压强小处流
D、水一定是从测压管水头高处向测压管水头低处流 E、水一定是从机械能大处向机械能小处流
三、判断改错题(本大题共5小题,每小题3分,共15分)判断正误,将正确的划上“√”,
错误的划上“×”,并改正错误。
21.流体的黏性随着温度的增加而减小。( ) 22.流线一般不能相交,且只能是一条光滑曲线。( )
23.明渠均匀流的渠底坡度、水面线坡度和总水头线坡度恒相等。( ) 24.均匀流是指运动要素不随时间变化的流动。( )
25.在工程流体力学中,单位质量力是指作用在单位重量流体上的质量力。( ) 四、简答题(10分)
26.简述平衡流体中的应力特征。
五、计算题(本大题共5小题,每小题10分,共50分)
27.已知并联管路两支路的比阻之比S1/S21,管长之比l1/l22,则其相应的流
量之比Q1/Q2。
28.已知某高层建筑在风速为8m/s时,其迎风面和背风面测点的压强分别为40N/m 和
2
-20N/m,试求当风速为16m/s时,迎风面和背风面相应测点的压强。 29. 试设计一矩形断面小桥孔径B。已知设计流量Q30m/s,桥下游水深h1.1m,
桥下铺砌的允许流速v3.5m/s,桥前允许壅水水深H1.5m,选定小桥进口形式后知0.85,0.90,取动能修正系数1.0。
30. 试设计一长直梯形断面运河的底宽b和底坡i。已知流量Q30m/s,边坡系数
3
3
2
m1.5,糙率系数n0.025,由于航运,要求流速v0.8m/s,水深h2.0m。
31. 如图所示为绕铰链C 转动的自动开启式矩形平板闸门。已知闸门倾角为600,
宽度为b5m,闸门两侧水深分别为H4m和h2m,为避免闸门自动开启,试求转轴C至闸门下端B的距离x。
参考答案
一、单项选择题(1×15=15分)
1.B 2.D 3.D 4.B 5.C 6.B 7.A 8.A 9.A 10.D 11.D 12.B 13.A 14.B 15.D 二、多项选择题(2×5=10分)
16.ABC 17.ACDE 18.AD 19.ABCDE 20.ABCD 三、判断改错题(3×5=15分)
21.( × )液体的黏性随着温度的增加而减小。 22.( × )流线愈密,流速愈大。 23.( √ ) 24.( × )恒定流是指运动要素不随时间变化的流动或均匀流是指流线为平行直线的流动。 25.( × )在工程流体力学中,单位质量力是指作用在单位质量流体上的质量力。 四、简答题(10分)
26.方向性:平衡流体中的应力垂直指向受压面;(5分)
大小性:平衡流体中任一点的压强大小与作用方位无关,即pf(x,y,z)。(5分)
五、计算题(10×5=45分) 27.据题意有
hf1hf2S1l1Q121 (5分) 2
S2l2Q2
故
Q1
Q2S2l2
0.707 (5分) S1l1
28.由欧拉准则
p
1 得 2
v
pppm
(vpvm
2v
p
vpvm
)2 (4分)
故原型迎风面 p1p(
)2p1m160Pa (3分)
背风面 p2p(
vpvm
)2p2m80Pa (3分)
29. 从vv出发进行设计:
①判别流动状态 hk
2v2
g
0.903m
因1.3hk1.17mh1.1m,故小桥过流为自由式。 (3分) ②计算孔径 b
Q
h
13.14m
kv 取标准孔径B16m ③校核 hk3Q2
g(B)2
0.792m
1.3hk
1.03mh,已转为淹没式过流。 v
Q
Bh
2.01m/s Hv2
2g
2
h1.35mH(可以) 30. 由QAv得A
Q
v
37.5m2 (2分) 由A(bmh)h得bA
h
mh15.7m 因R
A
A
63m b2hm
2
1.故i(
vnR
2/3
)22.08104
31.为避免闸门自动打开,由理论力学知必有关系
PH左(x
3sin)Ph
右(x3sin) 式中 P1212
左2bH,P右2bh
H3故 xh3
3(H2h2
)sin
1.796m (3分)
(4分) 3分)
2分)
3分) (5分) (5分) (((
浅论工程流体力学
中图分类号:o368 文献标识:a 文章编号:
1009-4202(2011)07-000-01
摘要工程流体力学在工程中广泛应用,本文对工程流体力学的背景,发展,内容,应用,分支和前景做了简单介绍。
关键词工程流体力学 发展史 内容应用 发展前景
一、背景
在人类历史上,面对河道决堤,洪期到来,人类束手无策的案例数不胜数,还有河田的干旱,河运交通的堵塞给人类带来的不便也是不计其数。但是随着人类文明的发展,人类开始对河水治理,桥梁建造,农业灌溉,河水航运等有了较多的需求,人类同时也就对水流运动的规律有了较多的需求和经验。但是要合理自如的控制和运用流体,人类就需要一个比较系统的学科理论去指导,于是工程流体力学的诞生已经迫在眉睫。
二、发展史
中国史上的大禹治水,李冰父子建立的都江堰,就是对水认识的萌芽,古罗马人也在早期就建立起了比较完善的供水管道系统。但是对流体力学一个比较科学的认识还是要在公元前250年左右古希腊伟大的科学家阿基米德写的《论浮体》后,这本书对流体运动做了一个比较科学的总结,可以算得上是流体力学的鼻祖了。很遗憾的是在接下来的很长一段时间内,因为种种原因,流体力学并没有得到进一步发展。直到16世纪以后,西方资本主义国家的生产力
黑龙江工业学院
结课论文
《工程流体力学》
姓 名: 闫振斌
学 号: 0703****007
年 级: 2012级
学科专业: 煤矿开采技术
二级院系: 资源系
日 期: 2014-11-25
工程流体力学论文
摘要:流体力学是介于基础科学和工程技术之间,起着承上启下作用的一门技术基础科学。流体力学是力学的一个独立分支,是一门研究流体(液体和气体) 的平衡和力学运动规律及其应用的科学。它所研究的基本规律包括两大部 分:一是流体平衡的规律,即流体静力学;二是流体运动的规律,即流体 动力学。工程流体力学在工程中广泛应用,本文对工程流体力学的背景,发展,内容,应用,分支和前景做了简单介绍。
关键词:工程流体力学认识; 发展史 ;内容应用;理论分析 流体力学包括的内容
一、流体的的属性(流体的主要物理性质、流体的黏性及牛顿内摩擦定律、作用在流体上的力)
二、流体静力学(静止流体的应力特征、静止流体力的平衡、流体静压力强的分布规律、压强的度量和测量、流体作用在平面上的压力、液体作用在曲面上的压力)
三、流体运动学及动力学基础(描述流体质点运动的两种方法、流体运动的基本概念、流体运动的分类、流体运动的连续性方程、理想流体的运动微分方程、恒定元流总流的伯努利方程、恒定总流的动量方程)
四、管内流动与水力计算(流体阻力和水头损失、圆管中的层流和湍流、沿程水头损失和局部水头损失、管路的水力计算、有压管中的水击、边界层和绕流阻力)
五、明渠流、堰流和渗流(明渠流的分类、明渠均匀流、堰流、渗流)
六、相似性原理和量纲分析(相似性原理的定义及应用、几何相似、运动相似和动力相似、相似准则、量纲分析)
在人类历史上,面对河道决堤,洪期到来,人类束手无策的案例数不胜数,还有河田的干旱,河运交通的堵塞给人类带来的不便也是不计其数。但是随着人类文明的发展,人类开始对河水治理,桥梁建造,农业灌溉,河水航运等有了较多的需求,人类同时也就对水流运动的规律有了较多的需求和经验。但是要合理自如的控制和运用流体,人类就需要一个比较系统的学科理论去指导,于是工程流体力学的诞生已经迫在眉睫。
其实,我对流体力学的认识还仅仅出于感性认识的阶段,并没有很深入地了解流体力学的知识,对于一些同流体有关的现象并不能够运用相应的知识理论来进行解释。通过查阅资料,我了解到流体力学是研究流体的力学运动规律及其应用的学科。作为力学的一个重要分支,流体力学主要研究流体本身的静止状态和运动状态,以及流体和固体界壁之间具有相对运动时的相互作用及流动过程中动量,能量和质量的传输规律等,并将它们应用于解决生产,科研和生活中与流体运动有关的各种
问题。流体力学的研究对象包括水, 空气,水蒸气,润滑油,地下石油,血液,超高压作用下的金属盒燃烧后产生的成分复杂的气体,高温条件下的等离子体等等,其中研究得最多的是人类不可或缺的两种物质:水和空气。流体力学的研究只要是牛顿运动定律和质量守恒定律,此外常常还需要运用到热力学知识,又是还应用到宏观电动力学的基本定律,本构方程和物理学,化学的基本知识等等。
不仅如此,流体力学还具有广泛的应用范围,包括了工业,农业,军事等众多领域,既包含自然科学的基础理论,又涉及工程技术科学方面的应用,比如气象,水利,船舶,航空航天,机械制造,医疗以及天文研究等等都应用和涉及到了流体力学的知识。水和空气对于生命体来说是至关重要的,地球百分之七十的面积被水覆盖同事也被大气完全包围住,时刻在进行着对流和迁移运动,输送水分和热量,影响着全球的气候和生态环境;室友和天然气的开采;地下水的开发利用;沙漠迁移等等这些都同人们日常生活有着密切联系。也正是如此,对于流体力学的发展,就不会有现代工业以及高新技术的发展。流体力学对推动社会向前发展做出了巨大贡献,今后仍将在科学与技术的各个领域中发挥更大的作用。
流体力学的发展及展望
关于它的发展史是中国史上的大禹治水,李冰父子建立的都江堰,就是对水认识的萌芽,直到15世纪,意大利达·芬奇的著作才谈到水波管流、水力机械、鸟的飞翔原理等问题;古罗马人也在早期就建立起了比
较完善的供水管道系统。但是对流体力学一个比较科学的认识还是要在公元前250年左右古希腊伟大的科学家阿基米德写的《论浮体》后,这本书对流体运动做了一个比较科学的总结,可以算得上是流体力学的鼻祖了。很遗憾的是在接下来的很长一段时间内,因为种种原因,流体力学并没有得到进一步发展。直到16世纪以后,西方资本主义国家的生产力的迅速发展和资本主义制度的不断完善,以及政府对科学事业的政策和资金的鼓励,这才给各科学以及流体力学发展创造了良好的环境。
17世纪,力学奠基人、人类伟大的科学家牛顿对流体有了初步比较深入的研究,他通过不断试验提出了牛顿内摩擦定律,黏性运动的流体符合牛顿摩擦定律。接着拉格朗日和欧拉提出了描述流体运动的二种方法拉格朗日法和欧拉法,拉格朗日法着眼于流体个支点的运动情况,研究各质点的运动历程,最后综合来获得总体情况,欧拉法责只着眼于流体经过流场中各空间点时的运动情况。然后有普朗特的混合长度理论,法国皮托发明了测流速的皮托管,达朗贝尔利用这些得出了流体中运动的物体阻力于速度有平方关系。19世纪以后,随着生产力的进一步发展,尤其是航空方面的运用,导致古典流体力学和实验流体力学的日益结合,逐渐形成了理论与实践并重的现代流体力学。随后流体力学进入新的阶段。
流体力学的应用
流体力学广泛应用在航天,石油和天然气开采,地下水的开发利用,武器的爆炸,沙漠迁移等等,但是工程流体力学基本是指在工程中的应
用,包括城市的生活和工业用水,水厂修建水塔,这些就需要计算好各水井的布置位置,水管直径,长度,动力,途径等等。另外在,桥梁上,就需要对河水各个数据的掌握,以便对桥梁涵洞,配筋的设计。还有就是在高层建筑中,我们也要运用到空气动力学研究风荷载对建筑物的影响。在通风内燃机等的设计中,还要计算好空气流动规律,以便控制空气流量,燃气输送,降尘降温等留力学问题。我国的三峡大坝,葛洲坝等各大水利枢纽工程就是流体力学的宏伟体现。还有我国近年来航天工程中对流体力学的运用也是淋漓尽致。
理论分析:
理论分析(理论研究方法)是根据流体运动的普遍规律如质量守恒、动量守恒、能量守恒等,利用数学分析的手段,研究流体的运动,解释已知的现象,预测可能发生的结果。
结论:
从人类开始接触认识流体力学到现在的2千多年,特别是20世纪以来工程流体力学得到了广泛的应用和飞速的发展。人类已经可以用现有的理论体系去解决生活中,的绝大多数问题。但是人类对流体力学并没有完全了解,比如一些复杂的流体运动人类还是无法用系统科学的理论去解释,只能凭靠经验去解决许多问题,所以流体力学有很大的发展前景流体力学还需要我们去完善它的理论基础以及提出新的理论。 参考文献:
[1]赵嵩颖.工程流体力学.航空工业出版社
[2]闻德荪,李兆年,黄正华.工程流体力学(水力学)(第2版)[M].北京:高等教育出版社,2005. [3]伍悦滨,王芳.工程流体力学(水力学)[M].北京:中国建筑工业出版社,2006.
中图分类号:O368 文献标识:A 文章编号:1009-4202(2011)07-000-01 摘要工程流体力学在工程中广泛应用,本文对工程流体力学的背景,发展,内容,应用,分支和前景做了简单介绍。 关键词工程流体力学 发展史 内容应用 发展前景 一、背景 在人类历史上,面对河道决堤,洪期到来,人类束手无策的案例数不胜数,还有河田的干旱,河运交通的堵塞给人类带来的不便也是不计其数。但是随着人类文明的发展,人类开始对河水治理,桥梁建造,农业灌溉,河水航运等有了较多的需求,人类同时也就对水流运动的规律有了较多的需求和经验。但是要合理自如的控制和运用流体,人类就需要一个比较系统的学科理论去指导,于是工程流体力学的诞生已经迫在眉睫。 二、发展史 中国史上的大禹治水,李冰父子建立的都江堰,就是对水认识的萌芽,古罗马人也在早期就建立起了比较完善的供水管道系统。但是对流体力学一个比较科学的认识还是要在公元前250年左右古希腊伟大的科学家阿基米德写的《论浮体》后,这本书对流体运动做了一个比较科学的总结,可以算得上是流体力学的鼻祖了。很遗憾的是在接下来的很长一段时间内,因为种种原因,流体力学并没有得到进一步发展。直到16世纪以后,西方资本主义国家的生产力的迅速发展和资本主义制度的不断完善,以及政府对科学事业的政策和资金的鼓励,这才给各科学以及流体力学发展创造了良好的环境。 17世纪,人类伟大的科学家牛顿对流体有了初步比较深入的研究,他通过不断试验提出了牛顿内摩擦定律,黏性运动的流体符合牛顿摩擦定律。接着拉格朗日和欧拉提出了描述流体运动的二种方法拉格朗日法和欧拉法,拉格朗日法着眼于流体个支点的运动情况,研究各质点的运动历程,最后综合来获得总体情况,欧拉法责只着眼于流体经过流场中各空间点时的运动情况。然后有普朗特的混合长度理论,法国皮托发明了测流速的皮托管,达朗贝尔利用这些得出了流体中运动的物体阻力于速度有平方关系。欧拉总结出了欧拉运动微分方程(z+p/ρg+u*u/2g=C),伯努利又对管道流体做了多次试验得出了经典的伯努力方程(p+ρgz+(1/2)*ρv^2=C式中p、ρ、v分别为流体的压强、密度和速度;z 为铅垂高度;g为重力加速度。),它是能量守恒和转换定律在工程流体力学中的具体体现。19世纪以后,随着生产力的进一步发展,尤其是航空方面的运用,导致古典流体力学和实验流体力学的日益结合,逐渐形成了理论与实践并重的现代流体力学。随后流体力学进入新的阶段。 三、研究内容及应用 工程流体力学是一门研究工程中气体和液体运动规律的一门学科,他是基础力学的一个分支,它主要是以牛顿运动定律和质量守恒定律为基础的。流体力学有三个基本及假设:质量守恒,动量守恒,连续体假设。 流体力学广泛应用在航天,石油和天然气开采,地下水的开发利用,武器的爆炸,沙漠迁移等等,但是工程流体力学基本是指在工程中的应用,包括城市的生活和工业用水,水厂修建水塔,这些就需要计算好各水井的布置位置,水管直径,长度,动力,途径等等。另外在桥梁上,就需要对河水各个数据的掌握,以便对桥梁涵洞,配筋的设计。还有就是在高层建筑中,我们也要运用到空气动力学研究风荷载对建筑物的影响。在通风内燃机等的设计中,还要计算好空气流动规律,以便控制空气流量,燃气输送,降尘降温等留力学问题。我国的三峡大坝,葛洲坝等各大水利枢纽工程就是流体力学的宏伟体现。还有我国近年来航天工程中对流体力学的运用也是淋漓尽致。 四、研究方法 工程流体力学研究方法同一般科学研究方法大同小异,主要还是归结在现场观测,实验总结,建立理论,数值计算等。由于流体力学理论的不健全性,实验总结和现场观测尤为重要,流体力学应建立比较完善的观测站,另外还需要建立足够实验室去不断实验,不断模拟实践得出总结性结论。 五、流体力学分支 近几十年来,流体力学科学随着现代化生产建设的飞速发展和近代科学技术的不断进步,研究的范围越来越广,新的科学分支不断涌现出来,比如计算流体力学,随机流体力学,环境流体力学,能源流体力学,工业流体力学等等。 六、发展前景 从人类开始接触认识流体力学到现在的2千多年,特别是20世纪以来工程流体力学得到了广泛的应用和飞速的发展。人类已经可以用现有的理论体系去解决生活中的绝大多数问题。但是人类对流体力学并没有完全了解,比如一些复杂的流体运动人类还是无法用系统科学的理论去解释,只能凭靠经验去解决许多问题,所以流体力学有很大的发展前景流体力学还需要我们去完善它的理论基础以及提出新的理论。 参考文献: [1]禹华谦.工程流体力学.西南交大出版社. [2]朱自强.应用计算流体力学.北京:北京航空航天大学出版社.1998.8. [3]李亚东.土木工程专业英语.西南交通大学出版社.
工程流体力学论文
谢松伶
(长沙理工大学城南学院,建筑1103班,201189*****4)
摘要:流体力学是力学的一个独立分支,是一门研究流体(液体和气体) 的平衡和力学运动规律及其应用的科学。它所研究的基本规律包括两大部 分:一是流体平衡的规律,即流体静力学;二是流体运动的规律,即流体 动力学。工程流体力学在工程中广泛应用,本文对工程流体力学的背景,发展,内容,应用,分支和前景做了简单介绍。
关键词:工程流体力学认识; 发展史 ;内容应用;建筑工程与流体学。
引言
在人类历史上,面对河道决堤,洪期到来,人类束手无策的案例数不胜数,还有河田的干旱,河运交通的堵塞给人类带来的不便也是不计其数。但是随着人类文明的发展,人类开始对河水治理,桥梁建造,农业灌溉,河水航运等有了较多的需求,人类同时也就对水流运动的规律有了较多的需求和经验。但是要合理自如的控制和运用流体,人类就需要一个比较系统的学科理论去指导,于是工程流体力学的诞生已经迫在眉睫。
正文 其实,我对流体力学的认识还仅仅出于感性认识的阶段,并没有很深入地了解流体力学的知识,对于一些同流体有关的现象并不能够运用相应的知识理论来进行解释。通过查阅资料,我了解到流体力学是研究流体的力学运动规律及其应用的学科。作为力学的一个重要分支,流体力学主要研究流体本身的静止状态和运动状态,以及流体和固体界壁之间具有相对运动时的相互作用及流动过程中动量,能量和质量的传输规律等,并将它们应用于解决生产,科研和生活中与流体运动有关的各种问题。流体力学的研究对象包括水,空气,水蒸气,润滑油,地下石油,,血液,超高压作用下的金属盒燃烧后产生的成分复杂的气体,高温条件下的等离子体等等,其中研究得最多的是人类不可或缺的两种物质:水和空气。流体力学的研究只要是牛顿运动定律和质量守恒定律,此外常常还需要运用到热力学知识,又是还应用到宏观电动力学的基本定律,本构方程和物理学,化学的基本知识等等。
不仅如此,流体力学还具有广泛的应用范围,包括了工业,农业,军事等众多领域,既包含自然科学的基础理论,又涉及工程技术科学方面的应用,比如气象,水利,船舶,航空航天,机械制造,医疗以及天文研究等等都应用和涉及到了流体力学的知识。水和空气对于生命体来说是至关重要的,地球百分之七十的面积被水覆盖同事也被大气完全包围住,时刻在进行着对流和迁移运动,输送水
分和热量,影响着全球的气候和生态环境;室友和天然气的开采;地下水的开发利用;沙漠迁移等等这些都同人们日常生活有着密切联系。也正是如此,对于流体力学的发展,就不会有现代工业以及高新技术的发展。流体力学对推动社会向前发展做出了巨大贡献,今后仍将在科学与技术的各个领域中发挥更大的作用。 关于它的发展史是中国史上的大禹治水,李冰父子建立的都江堰,就是对水认识的萌芽,古罗马人也在早期就建立起了比较完善的供水管道系统。但是对流体力学一个比较科学的认识还是要在公元前250年左右古希腊伟大的科学家阿基米德写的《论浮体》后,这本书对流体运动做了一个比较科学的总结,可以算得上是流体力学的鼻祖了。很遗憾的是在接下来的很长一段时间内,因为种种原因,流体力学并没有得到进一步发展。直到16世纪以后,西方资本主义国家的生产力的迅速发展和资本主义制度的不断完善,以及政府对科学事业的政策和资金的鼓励,这才给各科学以及流体力学发展创造了良好的环境。
17世纪,人类伟大的科学家牛顿对流体有了初步比较深入的研究,他通过不断试验提出了牛顿内摩擦定律,黏性运动的流体符合牛顿摩擦定律。接着拉格朗日和欧拉提出了描述流体运动的二种方法拉格朗日法和欧拉法,拉格朗日法着眼于流体个支点的运动情况,研究各质点的运动历程,最后综合来获得总体情况,欧拉法责只着眼于流体经过流场中各空间点时的运动情况。然后有普朗特的混合长度理论,法国皮托发明了测流速的皮托管,达朗贝尔利用这些得出了流体中运动的物体阻力于速度有平方关系。欧拉总结出了欧拉运动微分方程(z p/ρg u*u/2g=C),伯努利又对管道流体做了多次试验得出了经典的伯努力方程(p ρgz (1/2)*ρv^2=C式中p、ρ、v分别为流体的压强、密度和速度;z 为铅垂高度;g为重力加速度。),它是能量守恒和转换定律在工程流体力学中的具体体现。19世纪以后,随着生产力的进一步发展,尤其是航空方面的运用,导致古典流体力学和实验流体力学的日益结合,逐渐形成了理论与实践并重的现代流体力学。随后流体力学进入新的阶段。
流体力学广泛应用在航天,石油和天然气开采,地下水的开发利用,武器的爆炸,沙漠迁移等等,但是工程流体力学基本是指在工程中的应用,包括城市的生活和工业用水,水厂修建水塔,这些就需要计算好各水井的布置位置,水管直径,长度,动力,途径等等。另外在,桥梁上,就需要对河水各个数据的掌握,以便对桥梁涵洞,配筋的设计。还有就是在高层建筑中,我们也要运用到空气动力学研究风荷载对建筑物的影响。在通风内燃机等的设计中,还要计算好空气流动规律,以便控制空气流量,燃气输送,降尘降温等留力学问题。我国的三峡大坝,葛洲坝等各大水利枢纽工程就是流体力学的宏伟体现。还有我国近年来航天工程中对流体力学的运用也是淋漓尽致。
对于自己现在学的土木工程与建筑专业,这个建筑与土木工程专业是研究人类社会和生活所需要的基础设施建设的规划、设计、建造和维护的工程领域。其工程硕士学位授权单位培养从事区域规划,城市和村镇规划,城市设计,建筑与结构设计,市政工程设计,桥梁、道路与隧道工程设计,地下与水工结构设计及其勘测、施工、维护等高级工程技术人员。研修的主要课程有:政治理论课、外语课、数值分析、现代建筑设计及理论、现代规划原理与方法、现代建筑评论、城市社会学、环境心理学、现代建筑物理、工程弹塑性力学、高等结构力学、高等土力学、工程结构设计原理、基础工程、工程测试技术、计算机应用技术、优化原理与方法、建筑经济与管理等。由于本领域涉及建筑与土木两个学科,课程可视培养对象增减。
其相关领域:交通与运输工程、测绘工程、水利工程、环境工程、环境科学、计算机应用技术。而工程流体力学属于水利工程其中,这个能更加清楚明确的学习到专业知识和让我们能更好更快的明白它的本质。
对于学习和理解工程流体力学课程上,指导我们的是一位经验丰富又及其幽默的韩老师,他的教育主旨是,让我们在有限的时间内接受更多的人生道理,而对于工程流体力学的学科上,他更加的是提倡我们自学,在课堂上更多接触的是他的各种丰富的求学之路上的经验,给我们最多的就是社会的经验,所以在课堂上最多的不是睡觉的学生而更多是笑声和感慨,但也由于课堂上的学习时间有限,大量的作业后也是一对烦恼,同学也成说了句玩笑式的话:“老师就是教我们1+1等于2,而叫我们做的作业是1000+1000等于几的作业。”
结论
从人类开始接触认识流体力学到现在的2千多年,特别是20世纪以来工程流体力学得到了广泛的应用和飞速的发展。人类已经可以用现有的理论体系去解决生活中,的绝大多数问题。但是人类对流体力学并没有完全了解,比如一些复杂的流体运动人类还是无法用系统科学的理论去解释,只能凭靠经验去解决许多问题,所以流体力学有很大的发展前景流体力学还需要我们去完善它的理论基础以及提出新的理论。
1,结构风工程,高耸建筑物一般都要做风洞试验的。而大跨度柔性桥梁的抗风性能就是空气动力学的一个典型应用。从而有了CFD的蓬勃发展。
2,处于近海和江河中的建筑物,尤其是桥墩基础啦,都要考虑水文的,因此就有河流动力学这一方向。
3,基坑施工时一般要考虑地下水的,降水怎么计算也要用到流体力学。 4,隧道中的通风效应,如何计算隧道施工 运营中的通风问题,风机如何安置,采用哪种通风方式都是很典型的应用。
5,高速铁路隧道的空气动力学效应。这个越来越重视啦。由于高铁的速度高,进出隧道时都会产生活塞效应,搞不好还有“空气炮”,所以也要用到流体力学来解决这些问题,也是当前的一个热点。
6,修明渠和城市管网设计(市政工程)用到的基本上都是经典的流体力学。
我们可以从以上几个方面让流体力学和土木与建筑专业相结合并更好的学习,在以后的学习工作中得到明确的方向。
参考文献:工程流体力学教材工程流体力学论文
谢松伶
(长沙理工大学城南学院,建筑1103班,201189*****4)
摘要:流体力学是力学的一个独立分支,是一门研究流体(液体和气体) 的平衡和力学运动规律及其应用的科学。它所研究的基本规律包括两大部 分:一是流体平衡的规律,即流体静力学;二是流体运动的规律,即流体 动力学。工程流体力学在工程中广泛应用,本文对工程流体力学的背景,发展,内容,应用,分支和前景做了简单介绍。
关键词:工程流体力学认识; 发展史 ;内容应用;建筑工程与流体学。
引言
在人类历史上,面对河道决堤,洪期到来,人类束手无策的案例数不胜数,还有河田的干旱,河运交通的堵塞给人类带来的不便也是不计其数。但是随着人类文明的发展,人类开始对河水治理,桥梁建造,农业灌溉,河水航运等有了较多的需求,人类同时也就对水流运动的规律有了较多的需求和经验。但是要合理自如的控制和运用流体,人类就需要一个比较系统的学科理论去指导,于是工程流体力学的诞生已经迫在眉睫。
正文 其实,我对流体力学的认识还仅仅出于感性认识的阶段,并没有很深入地了解流体力学的知识,对于一些同流体有关的现象并不能够运用相应的知识理论来进行解释。通过查阅资料,我了解到流体力学是研究流体的力学运动规律及其应用的学科。作为力学的一个重要分支,流体力学主要研究流体本身的静止状态和运动状态,以及流体和固体界壁之间具有相对运动时的相互作用及流动过程中动量,能量和质量的传输规律等,并将它们应用于解决生产,科研和生活中与流体运动有关的各种问题。流体力学的研究对象包括水,空气,水蒸气,润滑油,地下石油,,血液,超高压作用下的金属盒燃烧后产生的成分复杂的气体,高温条件下的等离子体等等,其中研究得最多的是人类不可或缺的两种物质:水和空气。流体力学的研究只要是牛顿运动定律和质量守恒定律,此外常常还需要运用到热力学知识,又是还应用到宏观电动力学的基本定律,本构方程和物理学,化学的基本知识等等。
不仅如此,流体力学还具有广泛的应用范围,包括了工业,农业,军事等众多领域,既包含自然科学的基础理论,又涉及工程技术科学方面的应用,比如气象,水利,船舶,航空航天,机械制造,医疗以及天文研究等等都应用和涉及到了流体力学的知识。水和空气对于生命体来说是至关重要的,地球百分之七十的面积被水覆盖同事也被大气完全包围住,时刻在进行着对流和迁移运动,输送水
分和热量,影响着全球的气候和生态环境;室友和天然气的开采;地下水的开发利用;沙漠迁移等等这些都同人们日常生活有着密切联系。也正是如此,对于流体力学的发展,就不会有现代工业以及高新技术的发展。流体力学对推动社会向前发展做出了巨大贡献,今后仍将在科学与技术的各个领域中发挥更大的作用。 关于它的发展史是中国史上的大禹治水,李冰父子建立的都江堰,就是对水认识的萌芽,古罗马人也在早期就建立起了比较完善的供水管道系统。但是对流体力学一个比较科学的认识还是要在公元前250年左右古希腊伟大的科学家阿基米德写的《论浮体》后,这本书对流体运动做了一个比较科学的总结,可以算得上是流体力学的鼻祖了。很遗憾的是在接下来的很长一段时间内,因为种种原因,流体力学并没有得到进一步发展。直到16世纪以后,西方资本主义国家的生产力的迅速发展和资本主义制度的不断完善,以及政府对科学事业的政策和资金的鼓励,这才给各科学以及流体力学发展创造了良好的环境。
17世纪,人类伟大的科学家牛顿对流体有了初步比较深入的研究,他通过不断试验提出了牛顿内摩擦定律,黏性运动的流体符合牛顿摩擦定律。接着拉格朗日和欧拉提出了描述流体运动的二种方法拉格朗日法和欧拉法,拉格朗日法着眼于流体个支点的运动情况,研究各质点的运动历程,最后综合来获得总体情况,欧拉法责只着眼于流体经过流场中各空间点时的运动情况。然后有普朗特的混合长度理论,法国皮托发明了测流速的皮托管,达朗贝尔利用这些得出了流体中运动的物体阻力于速度有平方关系。欧拉总结出了欧拉运动微分方程(z p/ρg u*u/2g=C),伯努利又对管道流体做了多次试验得出了经典的伯努力方程(p ρgz (1/2)*ρv^2=C式中p、ρ、v分别为流体的压强、密度和速度;z 为铅垂高度;g为重力加速度。),它是能量守恒和转换定律在工程流体力学中的具体体现。19世纪以后,随着生产力的进一步发展,尤其是航空方面的运用,导致古典流体力学和实验流体力学的日益结合,逐渐形成了理论与实践并重的现代流体力学。随后流体力学进入新的阶段。
流体力学广泛应用在航天,石油和天然气开采,地下水的开发利用,武器的爆炸,沙漠迁移等等,但是工程流体力学基本是指在工程中的应用,包括城市的生活和工业用水,水厂修建水塔,这些就需要计算好各水井的布置位置,水管直径,长度,动力,途径等等。另外在,桥梁上,就需要对河水各个数据的掌握,以便对桥梁涵洞,配筋的设计。还有就是在高层建筑中,我们也要运用到空气动力学研究风荷载对建筑物的影响。在通风内燃机等的设计中,还要计算好空气流动规律,以便控制空气流量,燃气输送,降尘降温等留力学问题。我国的三峡大坝,葛洲坝等各大水利枢纽工程就是流体力学的宏伟体现。还有我国近年来航天工程中对流体力学的运用也是淋漓尽致。
对于自己现在学的土木工程与建筑专业,这个建筑与土木工程专业是研究人类社会和生活所需要的基础设施建设的规划、设计、建造和维护的工程领域。其工程硕士学位授权单位培养从事区域规划,城市和村镇规划,城市设计,建筑与结构设计,市政工程设计,桥梁、道路与隧道工程设计,地下与水工结构设计及其勘测、施工、维护等高级工程技术人员。研修的主要课程有:政治理论课、外语课、数值分析、现代建筑设计及理论、现代规划原理与方法、现代建筑评论、城市社会学、环境心理学、现代建筑物理、工程弹塑性力学、高等结构力学、高等土力学、工程结构设计原理、基础工程、工程测试技术、计算机应用技术、优化原理与方法、建筑经济与管理等。由于本领域涉及建筑与土木两个学科,课程可视培养对象增减。
其相关领域:交通与运输工程、测绘工程、水利工程、环境工程、环境科学、计算机应用技术。而工程流体力学属于水利工程其中,这个能更加清楚明确的学习到专业知识和让我们能更好更快的明白它的本质。
对于学习和理解工程流体力学课程上,指导我们的是一位经验丰富又及其幽默的韩老师,他的教育主旨是,让我们在有限的时间内接受更多的人生道理,而对于工程流体力学的学科上,他更加的是提倡我们自学,在课堂上更多接触的是他的各种丰富的求学之路上的经验,给我们最多的就是社会的经验,所以在课堂上最多的不是睡觉的学生而更多是笑声和感慨,但也由于课堂上的学习时间有限,大量的作业后也是一对烦恼,同学也成说了句玩笑式的话:“老师就是教我们1+1等于2,而叫我们做的作业是1000+1000等于几的作业。”
结论

从人类开始接触认识流体力学到现在的2千多年,特别是20世纪以来工程流体力学得到了广泛的应用和飞速的发展。人类已经可以用现有的理论体系去解决生活中,的绝大多数问题。但是人类对流体力学并没有完全了解,比如一些复杂的流体运动人类还是无法用系统科学的理论去解释,只能凭靠经验去解决许多问题,所以流体力学有很大的发展前景流体力学还需要我们去完善它的理论基础以及提出新的理论。
1,结构风工程,高耸建筑物一般都要做风洞试验的。而大跨度柔性桥梁的抗风性能就是空气动力学的一个典型应用。从而有了CFD的蓬勃发展。
2,处于近海和江河中的建筑物,尤其是桥墩基础啦,都要考虑水文的,因此就有河流动力学这一方向。
3,基坑施工时一般要考虑地下水的,降水怎么计算也要用到流体力学。 4,隧道中的通风效应,如何计算隧道施工 运营中的通风问题,风机如何安置,采用哪种通风方式都是很典型的应用。
5,高速铁路隧道的空气动力学效应。这个越来越重视啦。由于高铁的速度高,进出隧道时都会产生活塞效应,搞不好还有“空气炮”,所以也要用到流体力学来解决这些问题,也是当前的一个热点。
6,修明渠和城市管网设计(市政工程)用到的基本上都是经典的流体力学。
我们可以从以上几个方面让流体力学和土木与建筑专业相结合并更好的学习,在以后的学习工作中得到明确的方向。
参考文献:工程流体力学教材
四、主观题
33. 简述流体的形态特征和力学特征。
答:形态特征:流体随容器而方圆,没有固定的形状。 力学特征:流体主要承受压力, 静止流体不能承受拉力和剪力。
34. 一封闭水箱如图所示,已知金属测压计读数面分别比A点高0.5m和1.5m,试求液面的绝对压强
Pa,金属测压计中心和容器内液和相对压强
。
答:
35. 如图所示为测量容器中A点压强的真空计。已知
试求A点的真空压 ,
强及真空度。
答:
36. 如图所示绕铰链C 转动的自动开启式矩形平板闸门。已知闸门倾角为
,宽度
为,闸门两侧水深分别为和,为避免闸门自动开启,试求转轴C至闸
门下端B的距离x。
答:
的市政排水管道施工质量。已知排水管堵
37. 利用检查井作闭水试验检验管径
头形心高程为256.34m,检查井中水面高程为259.04m,试求堵头所受的静水总压力大小。 答:
38. 如图所示盛水(重度为
)容器由半径为 R 的两个半球用 N 个螺栓连接而成,已知
测压管水位高出球顶 H ,试求每个螺栓所受的拉力 F
。答:
39. 如图所示水流流经等径直角弯管。已知管径mm,U形水银差压计读数
=300mm,管流速度
,试求相对压强
mm,管轴上A、B两点高差400m/s,相对压强
。
,
和 A、B两断面间的机械能损失
答:
40. 如图所示,为测流需要,在宽度
m的平底矩形断面渠道的测流段,将渠底抬高
经率定按抬高
0.3m。若测得抬高前的水深为1.8m,抬高后水面降低0.12m,水头损失
后流速水头的一半计算,试求渠道流量。答:
四、主观题
19. 为研究某铁路盖板箱涵无压过流的水力特征,拟取线性比尺已知原型涵洞的宽度
m ,高度
m ,洞内设计水深
进行水工模型实验。m
和设计流速
m/s 。试确定模型的几何尺寸和模型流量 答:
20. 已知钢筋混凝土输水管道的水力半径
损失
,管壁粗糙系数
,水以均匀流流过1km长度上的水头
,试求管中的流速和流量。
答:
21. 水从封闭容器A经直径
上的相对压强
、阀门
、弯道
、长度的管道流入容器B。已知容器A内水面
;局部阻力系数,进口
,沿程阻力系数
、出口
,试求管路的通过流量。
答:
,管道沿
22. 一城市排污渠道采用倒虹吸管穿过河流,如图所示。已知污水流量程阻力系数
,管道进口、弯头和出口的局部阻力系数分别为
,上、下游渠道的流速均为得小于
,管长
。为避免污物在管中沉积,要求管中流速不
。
,试确定倒虹吸管的管径及倒虹吸管两端的水位差
答:
23. 试按水力最优条件设计一路基排水沟的断面尺寸。设计流量地形条件采用数答:
)。
,断面采用边坡系数
,沟底坡度依
的梯形,并用小片石干砌护面(粗糙系
一、主观题
1.
简述堰流的定义及堰的分类。
2.
试设计一跨越矩形过流断面的小桥孔径 。已知河道设计流量(据水文计算得)m3/s,桥前允许壅水水深选定小桥进口形式后知
m,桥下铺砌允许流速
m/s,桥下游水深
。
m,
,取动能修正系数
答:
3.
简述渗流系数的确定方法。
答:经验法,室内测定法,野外测定法(或现场测定法)。
1.粘性2.流线曲线。3.流量 单位时间通过某一截面流体的数量。4.速度环量 在流场中某一瞬时速度沿某一封闭曲线的积分。5.边界层 在固壁附近速度梯度很大的薄层区域。
二.简答题(20分每题10分)
1.简述定常不可压粘性流体有压管流中层流和紊流的基本规律。
2.画出无限空间自由淹没紊流射流结构图,并说明其几何、运动、动力特征。
答:几何特征:tanα=3.4a、运动特征:各截面速度分布相似、动力特征:各截面动量相等。
三、选择与填空(30分)
1.两平板相距0.1mm,中间充满了粘度为μ=0.00114Pa/s的流体,上平板相对下平板的运动速度为3.5m/s,则平板表面的切应力为 39.9 Pa。(3分) 7.如图2所示,设
H=3m,不计损失,则出口速度为
m/s。(2分)
8.两水管的有压流动相似,d1/d2=3,则v2/v1。(2分)
10.理想不可压流体作平面无旋流动,其流函数为kxy,则vx=vy=
-ky 。(2分)
12.某正激波前速度系数为2.3,则波后速度系数为 0.435 。(1分) 13.如图5所示为小扰动在不同来流速度场的传播,则来流速度在图a中 B ,图b
中A 。(A.Ma>1 B.Ma<1 C.Ma=1=。(1分)
图5(a) 图5(b) 图6
14.设某管路的水力直径为4.8m,则其水力半径为。(1分) 15.某二元不可压流场,vx5x3,vy15x2y,则过点(1,2)的ax(2分)
22
17.某流场的速度分布为vxyiyxj4xyzk,则该流场为.不可压 B.可
压缩)。(2分)
19.为了获得超声速气流应使用A.收缩喷管 B.缩放喷管)。(1分) 1.流体是一种受任何微小 剪切力 作用时,都会产生连续变形的物质。 2.作用于流体上的力按其性质可以分为表面力和 质量力 。
z
p
cg 。
3.缓变流任意过流截面静压力分布特点:
4. 一边长为a的等边三角形截面管内充满流体流动,其当量直径(水力直径) di
3
a
3 。
vky
5. 某流场vxkx,y,则流线方程为 xyc 。 6.量纲和谐性原理是指任何一个正确的方程式中,各项的量纲必须 相同 7.在管流中,如果两个截面的直径比为
。1/2
8. 在圆管层流流动中,沿程损失与速度的 一次方 成正比。 9.某水流速度是2.5m/s,则其速度水头是 0.32 mH2O。
10.斯托克斯定理表明,沿封闭曲线的L的速度环量等于穿过以该曲线为周界的任意
曲面的 涡通量 。
22
xyx,其流函数为 2xyy 11.不可压缩平面流动的势函数为
,则这两个截面上的雷诺数之比为
12.边界层的分离只可能发生在 压强 升高的区域内,形成旋涡。 13.马赫数的定义为气体的流速与 当地声速 的比值。
14.超声速气流在扩压管中进行增压,扩压管的截面积应该逐渐 减少 ;超声速气
流在喷管中进行增速,喷管的截面积应该逐渐 增大 。 3.对于实际流体,总水头线是 沿程下降 的线。
4.理想流体与实际流体的主要区别在于 是否烤炉粘性 。 5.真空是指 绝对压强 和 当地大气压 的压力差。
6.Re是表征 粘性 力的相似准则数,在圆管流动中,当Re小于 2000 时,
实际流体的流动状态是 层流 流动;当Re大于该值时,其流动状态是 紊流 流动。
7.流体旋转质点的运动形式包括平移、 变形 和 旋转 。 8.气流速度与临界速度之比是 速度系数 。 9.亚声速流动,是指马赫数___小于1_______时的流动。
二、简答题(每题5分,共25分)
1、 什么是连续介质假设?引入连续介质假设的目的是什么?
连续介质假设认为流体是由空间上连续分布的流体质点组成的连续介质。根据流体的
连续介质模型,任意时刻流动空间的任一点都为相应的流体质点占据,表征流体性质和运动特征的物理量一般为时间和空间的连续函数,就可以应用数学分析中连续函数分析和解决流体力学问题。
2、 什么是水力光滑管?什么是水力粗糙管?
当流体流动过程中,粘性底层完全淹没了管壁粗糙凸出部分,这时粘性底层以外的紊
流区域完全感受不到管壁粗糙度的影响,流体好像在完全光滑的管子中流动,这种管道称为水力光滑管。当管壁的粗糙凸出部分有一部分或者大部分暴露在紊流区域中,这时流体流过凸出部分将产生旋涡,造成新的能量损失,这种管道称为粗糙管。
3、 什么是缓变流?缓变流的特征是什么?
当流线的曲率半径很大或流线之间的夹角很小时,流线近似为平行直线,这样的流动
称为缓变流。缓变流的特性:缓变流任意过流截面上流体静压力的分布规律与平衡流体中的相同
4、 试根据尼古拉兹试验,说明紊流各区沿程阻力系数 与 和 的关系。
对于粗糙管阻力系数λ与Re的关系可以分为五个阶段:当Re<2300时,流动处于层
流状态,管壁的相对粗糙度对阻力系数λ没有影响,λ与Re成反比关系;2300<Re<4000时,处于第一过渡区,是层流向紊流过渡的不稳定区域;4000<Re<26.98(d/ε)8/7时,为水力光滑管区,λ与Re的0.25次方成反比关系;26.98(d/ε)8/7<Re<4160(d/2ε)0.85时,为第二过渡区,随着Re的增大,λ也增加;4160(d/2ε)0.85<Re时,处于阻力平方区,λ与Re无关。
1.水管上安装一复式水银测压计如图所示。同一水平线上各点的压强p1、p2、p3、p4 哪
个最大?哪个最小?哪些相等? 答:P4最大,最小,P2=P3
2.在一条水平管段上装有两只测压管,如图2所示,当管
中P1
流量增大时,两只测压管中液面高度h1与h2是增大还是减小?并说明原因。 答: 减小, 增大,因为随着流量的增加,管中的绝对压力均减小, 测的压力为相
对压力, 测的压力为真空压力
3.已知液体中流速u沿y方向分布如图3所示,试根据牛顿内摩擦定律
性绘出切应力沿 y 方向的分布图。
du
dy, 定
4.关于水流去向问题,曾有以下一些说法,如“水一定是从高处流向低处”、“水是
由压力大的地方流向压力小的地方”、“水是由流速大的地方流向流速 小的地方”,这些说法对吗,试用基本方程式加以说明。
答:以上说法都不对,由粘性流体的伯努力方程可知,水是由机械能大的地方流向机
械能小的地方。
5.判断容器的加速度方向并说明理由。(其中J为单位质量力)
答:容器的加速度方向垂直向下。因为作用在容器内液体质点上的单位质量力J与所
对应的加速度大小方向相同,并且容器与其中的液体一起运动,因此容器的加速度方向也与 单位质量力的方向相同,垂直向下。
三.计算题(40分,每题10分)
1.如下图所示文丘里流量计,当水流过时汞差压计的读数为H=125mm,设d1=250mm,d2=100mm,不计损失,试求水的流量。
2.某排水管路系统如上图所示。排水管出口到吸水井液面的高差为Hc=530 m,吸水管直径d1= 0.25 m,长度L1= 40 m,λ1=0.025,∑ζ1=5。排水管直径d2=0.2 m,长度L2= 580 m,λ2=0.028,∑ζ2=3。不计空气造成的压力差。当流量qv=270 m3/小时,求水泵给单位重量流体所提供的能量)H。
3.如下图所示,一隔板将水箱分为A、B两格,隔板上有直径为dl=40毫米的薄壁小孔口,流量系数0.62。B箱底部有一直径径d2=30毫米的圆柱形管嘴,管嘴长0.1米,流量系数0.82。A箱水深H1=3米恒定不变。试求在定常出流时H1为多少?出流的流量是多少?
4.设某流场的流函数为ψ=2axy,试证明该流场无旋、不可压,并求其速度势函数。
二、简答题(每题5分,共25分)
1、解:平板沿斜面向下的作用力为:
FGsin2006.8
N
则平板上的切应力为:
F6.857A0.12
N/m2
dudy
根据牛顿内摩擦定律:
duUdyh 设速度分布为线性分布,则:则均速下滑时平板的速度U是:
U
57
h81030.70.65
m/s
1
1
2.解:设A到等压面1-1截面的距离为z,则有:
pA水zpB水(zha)h pApB水z水(zha)h pApB水(ha)h
9800*0.29000*0.1
1060Pa
3、解:因为水闸的内外均受大气压力作用,故大气压的影响可略去。 作用在闸门上的总压力为:
l
pghcAg(hsin30)bl
2
2.51
10009.8(3)1.52.5
22
133218.75(N)
(3分)
根据压力中心的计算公式,可得:
这个距离应该是闸门的延长线与水面的交点为原点算起的距离。式中,
yc
Icx
yDyc
IcxycA
hl32.5
7.25(m)sin3020.52
131
bl1.52.531.951212
Abl1.52.53.75
所以,
yD7.25
1.95h
7.32(m)p(yD)Fl0
7.253.75sin30
3
F133218.75(7.32)2.570339.5(N)
0.5对A点列合力矩方程,得:
V1
解:(1)
Q4QQ4Q
21.132m/sV24.527m/s2
AA1d1d22
取1-1、2-2两断面列伯努利方程
(2)对选取的控制体列动量方程:
p1A1RxQ(0V1) Ryp2A2Q(V20) 所以,
Rx3663N
2x
2y
Ry958N
RRR3786N
arctg
RyRx
14.66
所以,水流对弯管壁的作用力为F的反作用力F`,大小相等,方向相反。
5.某水塔供水系统,h=20m,由管路1、2组成,按长管计算,d1=250mm,l1=20m,d2=200mm,l2=260m,沿程阻力系数均为0.03,中间有水泵一台,泵的扬程是40mH2O,求管路中的流量。
lvlv
Hhhwh11
22
d12gd22gvlld
h1(1214)
2gd1d2d2
2
4
22
v120000260****504
40200.03()
2*9.8250200****
2
v12.004m/s q
4
d12*v1
4
*0.252*2.0040.098m3/s
1uyux1z()(2x2x)0
2xy2
6、解:(1)因为
duxdxuydy
所以流动为有势流动,即存在势函数。
13
xyayy
3
2
2
(2)因为
uxuy
2y2y0 xy
所以流动为不可压缩流体的流动,即存在流函数。
duxdyuydx
xy2(a2xx3)cxy2a2xx3
1313
5、解:取1-1、2-2两液面列伯努利方程:
z1z2hf1hf2
LV
hf1111
d12g
2
hf2
LV222
d22g
2
V12V224.41
取1-1、3-3两液面列伯努利方程:
Q1Q2Q3
z1z3hf1hf3V12V322.94d1d2d3V1V2V3
解方程(1)(2)(3)组成的方程组可得
V11.67m/s
V21.28m/sV0.39m/s3
Q20.251m3/s
23d1Q0.0765m/s 3Q1V10.3275m3/s 4
所以,
Q2
d22
4
V20.251m3/s Q3
d32
4
V30.0765m3/s
工程流体力学论文
学家、物约瑟夫·拉格朗日(Joseph-Louis Lagrange,1736~1813)全名为约瑟夫·路易斯·拉格朗日,法国著名数理学家。1736年1月25日生于意大利都灵,1813年4月10日卒于巴黎。他在数学、力学和天文学三个学科领域中都有历史性的贡献,其中尤以数学方面的成就最为突出 拉格朗日科学研究所涉及的领域极其广泛。他在数学上最突出的贡献是使数学分析与几何与力学脱离开来,使数学的独立性更为清楚,从此数学不再仅仅是其他学科的工具。
拉格朗日总结了18世纪的数学成果,同时又为19世纪的数学研究开辟了道路,堪称法国最杰出的数学大师。同时,他的关于月球运动(三体问题)、行星运动、轨道计算、两个不动中心问题、流体力学等方面的成果,在使天文学力学化、力学分析化上,也起到了历史性的作用,促进了力学和天体力学的进一步发展,成为这些领域的开创性或奠基性研究。
拉格朗日也是分析力学的创立者。拉格朗日在其名著《分析力学》中,在总结历史上各种力学基本原理的基础上,发展达朗贝尔、欧拉等人研究成果,引入了势和等势面的概念,进一步把数学分析应用于质点和刚体力学,提出了运用于静力学和动力学的普遍方程,引进广义坐标的概念,建立了拉格朗日方程,把力学体系的运动方程从以力为基本概念的牛顿形式,改变为以能量为基本概念的分析力学形式,
奠定了分析力学的基础,为把力学理论推广应用到物理学其他领域开辟了道路。
近百余年来,数学领域的许多新成就都可以直接或间接地溯源于拉格朗日的工作。所以他在数学史上被认为是对分析数学的发展产生全面影响的数学家之一。
拉格朗日在数学、力学和天文学三个学科中都有重大历史性贡献,但他主要是数学家,研究力学和天文学的目的是表明数学分析的威力。全部著作、论文、学术报告记录、学术通讯超过500篇。欧洲大陆则按莱布尼兹创立的分析方法(当时包括代数方法),进展很快,当时叫分析学(analysis)。拉格朗日是仅次于欧拉的最大开拓者,在18世纪创立的主要分支中都有开拓性贡献。
变分法:这是拉格朗日最早研究的领域,以欧拉的思路和结果为依据,但从纯分析方法出发,得到更完善的结果。拉格朗日方法是对积分进行极值化,函数y=y(x)待定。
微分方程:早在都灵时期,拉格朗日就对变系数常微分方程研究做出重大成果。他在降阶过程中提出了以后所称的伴随方程,并证明了非齐次线性变系数方程的伴随方程的伴随方程,就是原方程的齐次方程。他还把欧拉关于常系数齐次方程的结果推广到变系数情况,证明了变系数齐次方程的通解可用一些独立特解乘上任意常数相加而成;而且在知道方程的m个特解后,可以把方程降低m价。
方程论:18世纪的代数学从属于分析,方程论是其中的活跃领域。拉格朗日在柏林的前十年,大量时间花在代数方程和超越方程的解法上。
拉格朗日是18世纪的伟大科学家,在数学、力学和天文学三个学科中都有历史性的重大贡献。但他主要是数学家,拿破仑曾称赞他是“一座高耸在数学界的金字塔”,他最突出的贡献是在把数学分析的基础脱离几何与力学方面起了决定性的作用。使数学的独立性更为清楚,而不仅是其他学科的工具。同时在使天文学力学化、力学分析化上也起了历史性作用,促使力学和天文学(天体力学)更深入发展。由于历史的局限,严密性不够妨碍着他取得更多的成果。
维普资讯
・
20 ・ 0
热
能
动
力
工
程
2 0 年 06
汽压 力发 生较 大 变化 , 辨 识 模 型 仍 能较 好 地 跟 踪 但 系统 的动 态变 化 ; 然 在不 同 的负 荷 区 间辨 识 的精 虽 度 会有 所不 同 , 模 型 仍满 意 地 描 述 运行 工况 大 范 但 围变化 时实 际对 象 的动态特 征 ,这充 分说 明用本 文 方法建 立 的 锅 炉 主 汽 压 力 非 线 性 对 象 模 型 的有 效
性。
[ ] A T O B L_ Annier oefrt r nrt po 1 S R M KJ, E lRD. ol a m dlo e ag e i r- . n sa e a ̄ m cs sA]Po 2hIA es [ .rc1t F CWol o ges c]N wY r: eg- e r c nr E .e o Pr d k a
mo , 9 3. 9 t r 1 9 3 5—3 8. 9
[ ] A T O KJB L. 2 S R M ,E lRD. ya c dl o birubn tr t _ D nmimoe r oe- ri ae ao sf l t e ln r
u i :a os n a at  ̄ltJ f a10M ui RJS e nt dt g dpr e r s l iIo 6 W nt .w ・ s al a m ee at r [ [
d n: n nsi t fT c o o y, 9 l e Lu d I tt e o e hn l g l 9 u 3.
[] 3
HA E E HA B A, C N B I Mn删
( ) 11 4 :2 3—1 1 . 2 9
Z L _ A. dl ——MAT A yl C fzy E  ̄ ez
mo e fradu birtriesm m 【 JA tmaia20 ,9 dlo rm-a e- bn l u y J . uo t ,0 33 c
击
譬
、
[ ] 张箭 . 4 基于 B 网络 的锅炉过 热汽温 系统动态特 性的辨识 [ ] P J.
电 工 技 术学 报 ,97,2 5 :7 0 19 l( )5 —6 .
幽
[ ] N R A D 0.rin cretnto s:w yadhw ni - 5 E R N Ta igr ur e r n e n wk h n o ?A l hs ts ni r i nd ao clpoesm dl g J .1—. rn n N ua a r s oen [ ] —1E T a so erl c i IE E1
德
N t ok ,9 45 2 :7 —14 ew rs 19 , () 18 8 .
[] 刘红波 , 6 李少远 . 一种基于工况分 解的热工过 程非线性 控制模 型建立方 法及 应用 [ ] 控 制
理 论 与应 用 ,04 2 ( )7 5— j. 20 ,1 5 :8
图 1 5 % 一7 % 负荷 下主 蒸 汽压 力辨识 曲线 5 0
7 0. 9
[] 陈彦桥 , 7 刘吉臻 . 用 —s模糊模 型辨识 10M 协调控 制系统 6 W []华北电力大学学报 ,0 33 ( )3 —4 . J. 20 ,O4 :8 1 [] 李运泽 . 8 电厂热力 系统 的长期动 态特性模 型 [ ] 热能 动力工 J.
程 ,0 5加 ( )3 4 . 20 , 1 :8— 4
譬
、
【 ] T K G S G N Fzyietiao f y e adi pl 9 A A I U E O M.uz nt tno  ̄ r n sap - T. d ie i s m t i
幽
ct n oen n ot lJ .l—. rn yt ln C - a ost m dl gadcnr [] —g T a sSse la y i o i o l E g ms V
bre,95 1 ( )l6—12. ent18 。5 1 :1 3
德
[O 张小桃 . 1] 基于现场 数据与神经 网络 的热工对象 动态建模 [ ] J.
热 能 动 力 工 程 , 0 5加 ()3 —3 . 20 , 1 :5 7
( 渠 源 编辑 )
图 2 5 一9 % 负荷 下主 蒸汽压 力辨 识 曲线 7 % 0
5 结
论
针 对实 际工业 过 程 中多变量 、 线性 、 非 工况 范 围 广的特 点 , 本文 提 出了一 种 新 的基 于 —S模 型 的 在线 自适应 锅 炉主蒸 汽压 力 系统建模 方 案 。从 系统
输入输 出数 据 出发 , 用在 线模 糊 聚类 算 法对 一. 采 s
模型前 提规 则进 行 辨识 , 用 改进 的卡 尔 曼 滤 波辨 采
识局部 线性模 型 参 数 , 过 多个 局 部 线 性模 型 加权 通 合成就 可得 到 了锅 炉 主 蒸 汽压 力 系统 的全 局 模 型 。 与其 它非 线性过 程建 模方 法相 比 ,具有 计算 复 杂 程 度大 大降低 , 型结 构 更 适 于灵 活 的 在线 调 整 和 学 模 习算 法等 优点 。最后 以典 型 主蒸汽 压力 过程作 为对 象, 以现场 实 际数据 为依据 进 行 了仿 真研 究 , 真结 仿
果验证 了文 中提 出的模 型建模 方法 的有 效性 。 参 考文献 :
二 : 流体力学经典教程
第一章 流体流动
流体流动规律是本门课程的重要基础,主要原因 有以下三个方面: (1)流动阻力及流量计算 (2)流动对传热、传质及化学反应的影响 (3)流体的混合效果
1.1概述 概述
1.1.1流体流动的考察方法 1.1.2流体流动中的作用力 1.1.3流体流动中的机械能
1.1.1 流体流动的考察方法
气体合液体统称为流体。流体是由大量的 彼此间有一定间隙的单个分子所组成。不同的考 察方法对流体流动情况的理解也就不同。在物 理化学重(气体分子运动论)是考察单个分子 的微观运动,分子的运动是随机的、不规则的 混乱运动,在某一方向上有时有分子通过,有 时没有。因此这种考察方法认为流体是不连续 的介质,所需处理的运动是一种随机的运动, 问题将是非常复杂的。
(1)连续性假设
在化工原理中是考察液体质点的宏观运动,流体 质点是由大量分子组成的流体微团,其尺寸远小于设 备尺寸,但比起分子自由路程却要大的多。这样,可 以假定流体是有大量质点组成、彼此间没有间隙、完 全充满所占空间连续介质。流体的物性及运动参数在 空间作连续分布,从而可以使用连续函数的数学工具 加以描述。 在绝大多数情况下流体的连续性假设是成立的, 只是高真空稀薄气体的情况下连续性假定不成立。
(2)流体运动的描述方法
① 拉格朗日法 选定一个流体质点,对其跟踪观察,描 述其运动参数(位移、数度等)与时间的关系。可见, 拉格朗日法描述的是同一质点在不同时刻的状态。 ② 欧拉法 在固定的空间位置上观察 流体质点的运动 情况,直接描述各有关参数在空间各点的分布情况合 随时间的变化,例如对速度u,可作如下描述: 可见,欧拉法描述的是空间各点的状态及其与时 间的关系。
(3)定态流动(稳定流动,定常流动)
若空间各点的状态不随时间变化,改流动称为定态 流动。 ux,uy,yz,p,……=f(x,y,z) 与t 无关
(4)流线与轨线
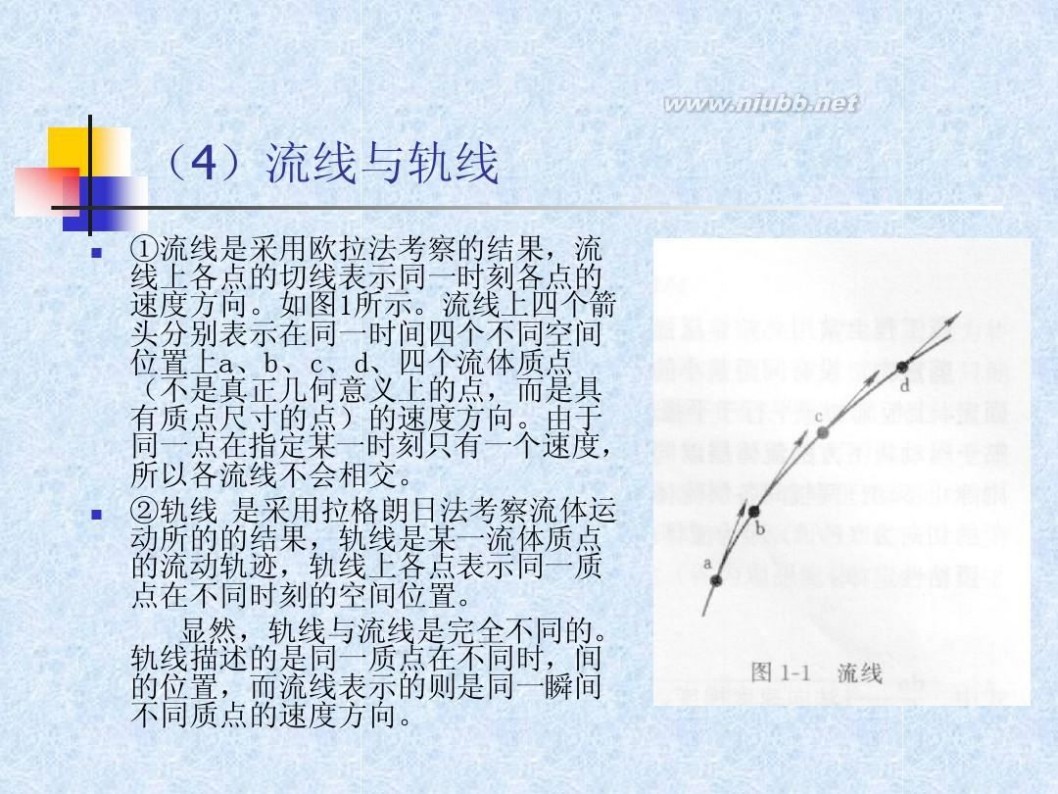
①流线是采用欧拉法考察的结果,流 线上各点的切线表示同一时刻各点的 速度方向。如图1所示。流线上四个箭 头分别表示在同一时间四个不同空间 位置上a、b、c、d、四个流体质点 (不是真正几何意义上的点,而是具 有质点尺寸的点)的速度方向。由于 同一点在指定某一时刻只有一个速度, 所以各流线不会相交。 ②轨线 是采用拉格朗日法考察流体运 动所的的结果,轨线是某一流体质点 的流动轨迹,轨线上各点表示同一质 点在不同时刻的空间位置。 显然,轨线与流线是完全不同的。 轨线描述的是同一质点在不同时,间 的位置,而流线表示的则是同一瞬间 不同质点的速度方向。
1.1
.1 流体流动的考察方法
(5)系统与控制体 (6)考察方法的选择
1.1.2流体流动中的作用力
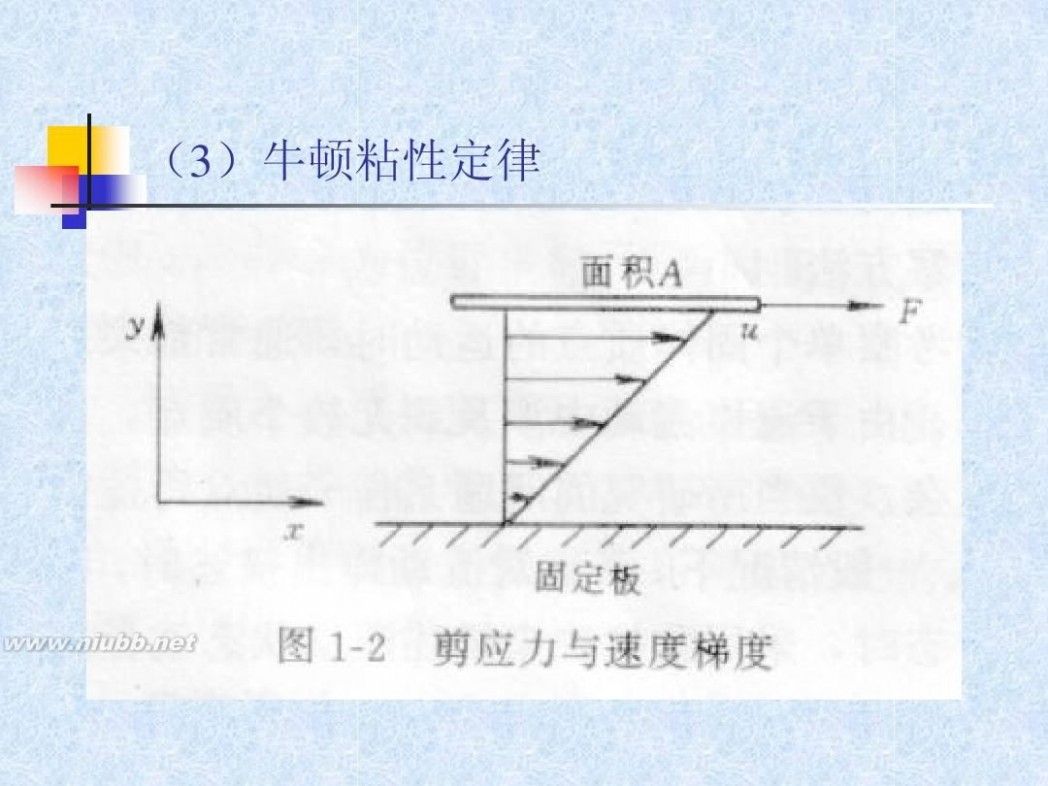
(1)体积力(质量力) (2)表面力 (3)牛顿粘性定律
(1)体积力(质量力)
与流体的质量成正比,对于均质的流体也与流体的体 积成正比。如流体在重力场中运动时受到的重力就是 一种体积力,F=mg。
(2)表面力
与流体的表面积成正比。若取流体中任一微小的平面,作用于其 上的表面力可分为 ①垂直与表面的力P,称为压力。单位面积上所受的压力称为压强p。
p(压强,N / m 2 ( Pa)) = P(压力,N) A(面积,m 2 )
1MPa(兆帕)=106Pa(帕斯卡) 注意:国内许多教材习惯上把压强称为压力。 ②平行于表面的力F,称为剪力(切力)。单位面积上所受的剪力称 为应力τ。 F(剪力,N) τ (剪应力,N/m 2) = A(面积,m 2)
(3)牛顿粘性定律
F du τ = =μ A dy
式中:μ——流体的粘度,Pa.s(N.s/m2);
du ——法向速度梯度,1/s。 dy
(3)牛顿粘性定律
①流体与固体的力学特性两个不同点
不同之一: 固体表面的剪应力τ∝剪切变形(角变形)dθ; 流体内部的剪应力τ∝剪切变形速率(角变形速率)
dθ du du = (见图1-3)。 dt dy
不同之二 静止流体不能承受剪应力(哪怕是非常微小的剪应力) 和抵抗剪切变形。固体可以承受很大的剪应力和抵抗 剪切变形。
①流体与固体的力学特性两个不同点
②流体的剪应力τ与动量传递
du du 根据牛顿粘性定律,对一定τ,μ↑, ↓;μ↓, ↑ dy dy
流动的流体内部相邻的速度不同的两流体层间存在相互作 用力,即速度快的流体层有着拖动与之相邻的速度慢的流 体层向前运动的力,而同时速度慢的流体层有着阻碍与之 相邻的速度快的流体层向前运动的力 流体内部速度不同的相邻两流体层之间的这种相互作用力 就称为流体的内摩擦力或粘性力F,单位面积上的F即为τ
③粘度μ的单位及换算关系
SI制: Pa ? s CGS制:cP(厘泊)
1Pa ? s = 1000cP或1cP=10 ?3 Pa ? s = 1mPa ? s
μ 运动粘度 υ = ρ
m 2 /s SI制的单位为
粘度μ又称为动力粘度。
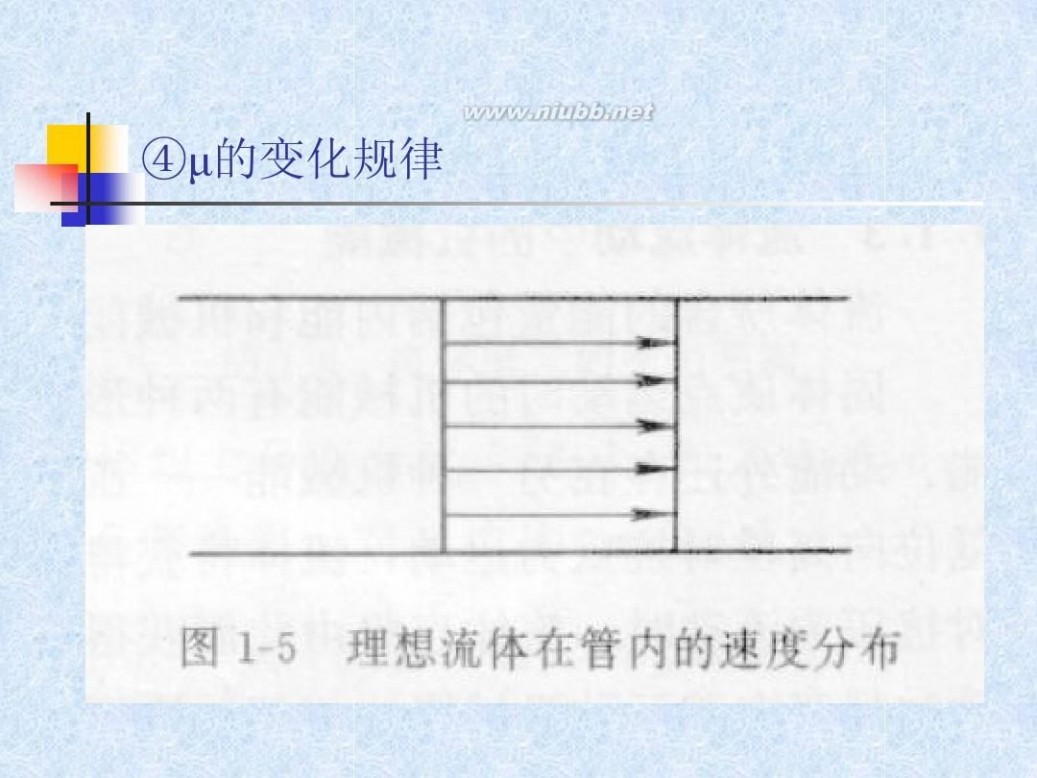
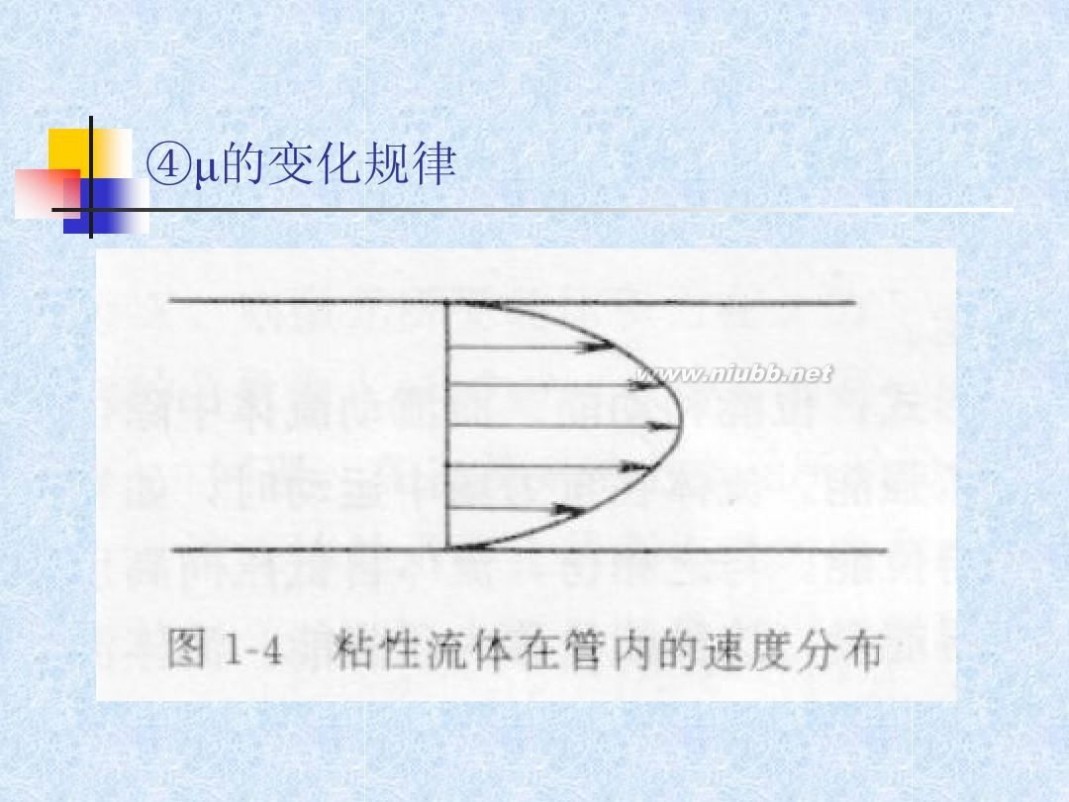
④μ的变化规律
液体:μ=f(t),与压强p无关,温度t↑,μ↓ 气体:p<40atm时μ=f(t)与p无关,温度t↑,μ↑ μ=0,流体无粘性(理想流体,图1-5,实际不存在)
④μ的变化规律
④μ的变化规律
服从牛顿粘性定律的流体称为牛顿型流体(大多数如 水、空气),本章主要研究牛顿型流体的流动规律, du 非牛顿型流体(血液、牙膏等)的τ与速度梯度 dy dy 关系见本章第8节。 如图1-4:
du τ = ?μ dy
u——半径r处的点速度,m/s
④μ的变化规律
1.1.3流体流动中的机械能
(1)内能 (2)位
能 (3)动能 (4)压强能 机械能(位能、动能、压强能)在流动过程可以 互相转换,亦可转变为热或流体的内能。但热和内能 在流体流动过程不能直接转变为机械能而用于流体输 送。
(1)内能
内能是贮存于液体内部的能量,是由于原子与分子的 运动及其相互作用存在的能量。因此液体的内能与其 状态有关。内能大小主要决定于液体的温度,而液体 的压力影响可以忽略。 单位质量流体所具有的内能U=f(t),J/Kg
(2)位能
在重力场中,液体高于某基准面所具有的能量称为液体的位能。 液体在距离基准面高度为z时的位能相当于流体从基准面提升 高度为z时重力对液体所作的功 单位质量流体所具有的位能gz
[ gz ] =
m m m N?m ? m=Kg ? 2 ? = =J/Kg 2 s s Kg Kg
(3)动能
液体因运动而具有的能量,称为动能
u2 单位质量流体所具有的动能 2
u2 m Kg ? m m N ? m [ ] = ( )2 = 2 ? = =J/Kg 2 s s Kg Kg
(4)压强能
流体自低压向高压对抗压力流动时,流体由此获得的 能量称为压强能 单位质量流体所具有的压强能 ρ = pv v——流体的比容(比体积), 3 /Kg m
N/m 2 N ? m [ ]= = =J/Kg 3 ρ Kg/m Kg p
p
1.2 流体静力学
1.2.1 静压强在空间的分布 1.2.2 压强能与位能 1.2.3 压强的表示方法 1.2.4压强的静力学测量方法
1.2.1静压强在空间的分布
(1)静压强 (2)流体微元的受力平衡 (3)平衡方程在重力场中的应用
(1)静压强
空间各点p=f(x,y,z)
某一点不同方向上的压强在数值上相等, 为什么?
(2)流体微元的受力平衡
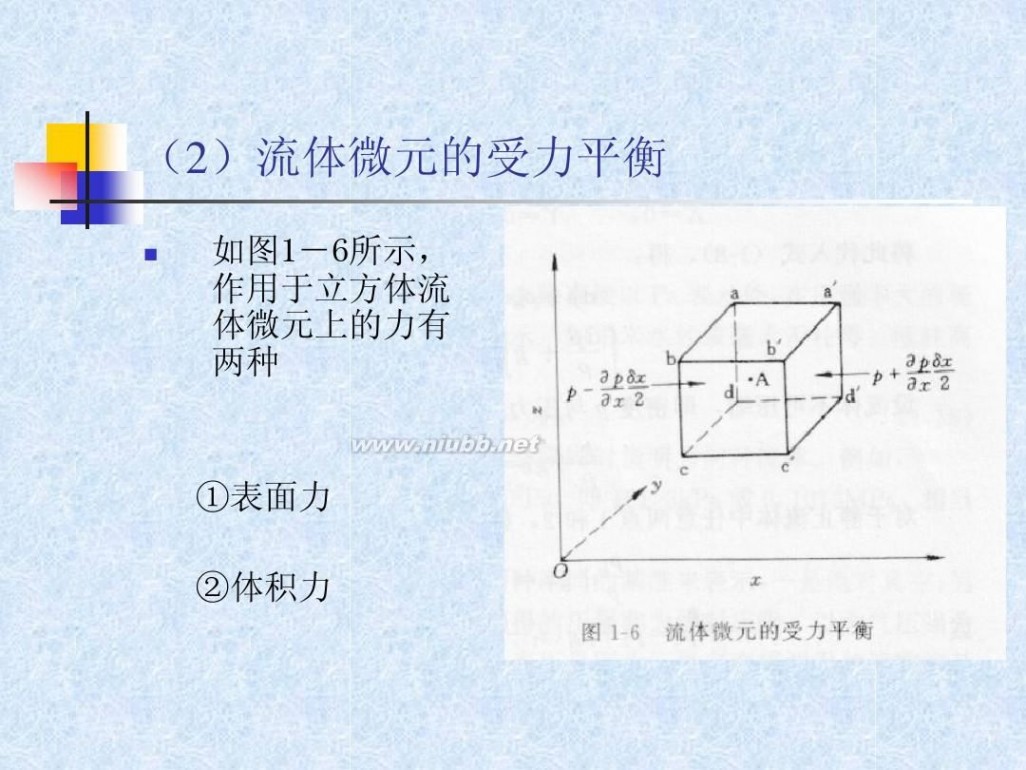
如图1-6所示, 作用于立方体流 体微元上的力有 两种
①表面力 ②体积力
①表面力
?p δx ( )δyδz abcd表面的压力(N)为: p ? ?x 2
( a’b’c’d’表面的压力(N)为: p + ?p δ x )δ yδ z ?x 2
对于其他表面,也可以写出相应的表达式
②体积力
设单位质量流体上的体积力在x方向的分量为x (N/Kg),则微元所受的体积力在x方向的分量 为 xρδxδyδz ,该流体处于静止状态,外力之和必 等于零、对x方向,有:
?p δ x ?p δ x (p? )δ yδ z ? ( p + )δ yδ z + x ρδ xδ yδ z = 0 ?x 2 ?x 2
与x方向相同的力取“+”号,相反取“-”号
②体积力
上式两边同除以 ρδxδyδz
X? 1 ?p =0 ρ ?x
得:
同理
1 ?p Y? =0 ρ ?x
Z? 1 ?p =0 ρ ?x
②体积力
若将该微元流体移动dl距离,此距离对x,y,z轴的分量 为dx、dy、dz,将上列方程组分别乘以dx、dy、dz并 相加得:
1 ?p ?p ?p ( dx + dy + dz ) ? ( Xdx + Ydy + Zdz ) = 0 ρ ?x ?y ?z
表示两种力对微元流体作功之和为零。
②体积力
由于静止流体压强仅与空间位置有关,即与时间无关。 所以上式左侧括号内即为压强的全
微分,于是:
dp
ρ
= Xdx + Ydy + Zdz (流体平衡的一般表达式)
dp
式中:
ρ
——压力作的功
Xdx + Ydy + Zdz ——体积力作的功
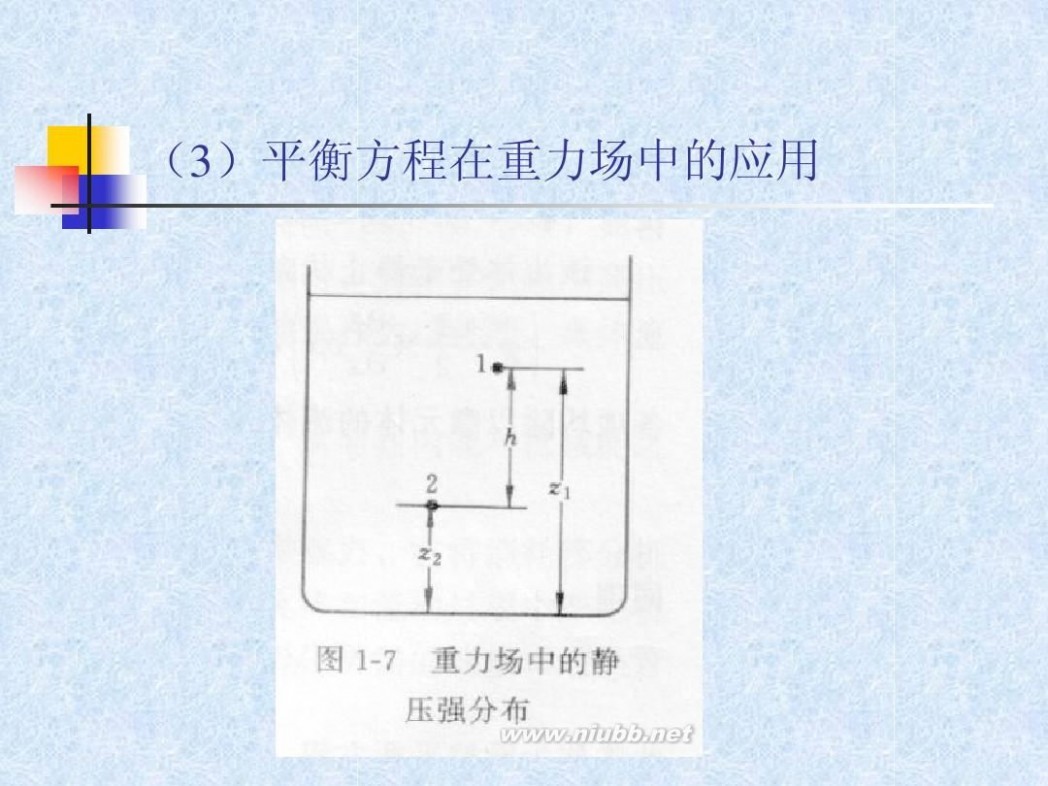
(3)平衡方程在重力场中的应用
如流体所受的体积力仅为重力,并取z轴方向与重力方 向相反,则: X=0,Y=0,Z=-g 将此式代入流体平衡的一般表达式有
dp + ρ g dz = 0
∫ρ
dp
+ g ∫ dz = 0
(3)平衡方程在重力场中的应用 设流体不可压缩,即密度ρ与压力无关,可将上式积 分得: p + gz = 常数 ρ 对于静止流体中任意两点1和2,如图1-7所示:
p1 p2
ρ
+ gz1 =
ρ
+ gz2
或
p2 = p1 + ρ g ( z1 ? z2 ) = p1 + ρ gh
(3)平衡方程在重力场中的应用
(3)平衡方程在重力场中的应用
必须指出,以上各式仅适用于在重力场中静止的不可 压缩流体。 静压强仅与垂直位置有关,而与水平位置无关。这是 由于流体仅处于重力场中的缘故。 流体中,液体的密度随压强的变化很小,可以认为是 不可压缩的流体;气体则不然,具有较大的可压缩性, 原则上上式不成立,但是若压强的变化不大,密度可 近似地取其平均值而视为常数时,以上各式仍可用。
1.3 流体流动中的守恒原理
以管流为主讨论流体质量守恒、能量守恒和动量守 恒,从而得到流速、压强等运动参数在流动过程中 的变化规律。 1.3.1 质量守恒 1.3.2 机械能守恒 1.3.3 动量守恒
1.3.1 质量守恒
(1)流量 (2)平均流速(简称流速)u (3)质量流速G (4)质量守恒方程
(1)流量
单位时间内流过管道某一截面的物质量称为流量。一 般有体积流量 qv 和质量流量 qm 两种表示方法。
qv 与 qm 的关系为:qm =qv ρ
式中:ρ——流体的密度,
(2)平均流速(简称流速)u
单位时间内流体在流动方向上所流过的距离称为流速 u(m/s)。
q V = uA = ∫ ur dA
A
式中:A——垂直于流动方向的管截面积 已知速度分布 ur 的表达式,求平均流速:
∫ u dA u=
A r
A
(3)质量流速G
单位时间内流体流过管道单位截面积的流体质量称为 质量流速G,其单位为 Kg/(m 2 ? s)。
qm G= = uρ A
(4)质量守恒方程
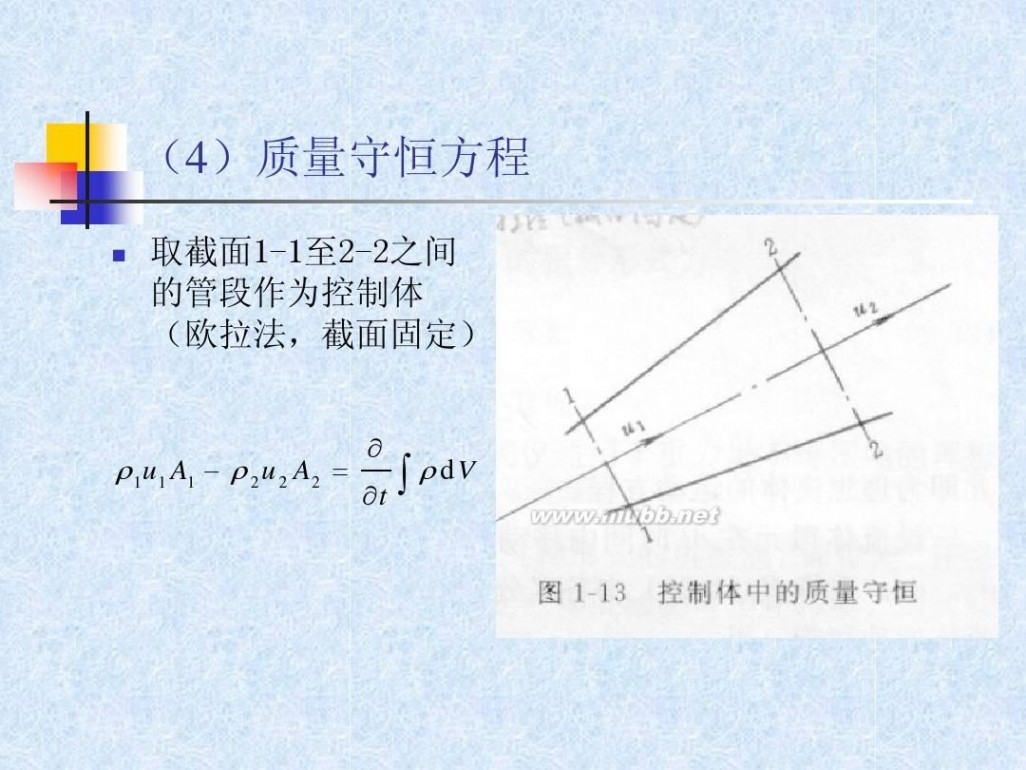
取截面1-1至2-2之间 的管段作为控制体 (欧拉法,截面固定)
? ρ1u1 A1 ? ρ 2u2 A2 = ∫ ρ dV ?t
(4)质量守恒方程
? 定态流动时 ∫ ρ dV = 0 ?t
ρ1u1 A1 = ρ 2 u 2 A2
对不可压缩流体 ρ1=ρ 2=常数
u1 A1 = u2 A2
对圆形截面管道 A =
π
4
d2
u 2 A1 d12 = = 2 u1 A2 d 2
1.3.2 机械能守恒
根据牛顿第二定律固体质点运动,无摩擦(理想条件) 机械能=位能+动能=常数 流体流动,无摩擦(理想流体,无粘性μ=0、F=0、 τ=0) 机械能=位能+动能+压强能=常数
u2 = 常数 单位质量流体所具有的机械能= gz + + ρ 2 p
1.3.2 机械
能守恒
(1)沿轨线(拉格朗日考察法,是某一流体质点的轨迹)的机械能守 恒 1 ?p 立方体微元所受各力平衡(静止): X ? =0 ρ ?x 在运动流体中,立方体微元表面不受剪应力,微元受力与静止流 体相同,但受力不平衡造成加速度,即: 1 ?p dux X? = ρ ?x dt 设流体微元在dt时间力位移dl,它在x轴上的分量位dx,将dx乘 上式各项得: 1 ?p du dx 1 2 X? dx = x dx = dux = ux dux = dux ρ ?x dt dt 2
1.3.2 机械能守恒
同理在y,z方向上有:
Y? 1 ?p 1 2 dy = du y ρ ?y 2
Z?
1 ?p 1 dz = du z2 ρ ?z 2
以上三式相加得 1 ?P ?p ?p 1 1 2 2 2 2 Xdx + Ydy + Zdz- ( dx + dy + dz ) = dux + duy + duz = du ρ ?x ?y ?z 2 2
(
)
1.3.2 机械能守恒
若流体仅在重力场中流动,取z轴垂直向上,则: X=0,Y=0,Z=-g 上式成为: dp 1
gdz + + du 2 = 0 ρ 2
对不可压缩流体,ρ=常数,积分上式得:
u2 gdz + + = 常数 ρ 2 p
p u2 + = 常数 ρ 2
上式适用于理想流体(μ =0),沿轨线机械能守恒。
1.3.2 机械能守恒
(2)沿流线(欧拉考擦法,固定截面上考擦)的机械能守恒定态流动, 流线与轨迹线重合,上式仍适用。 (3)理想流体管流的机械能衡算 理想流体( μ =0,τ=0,无阻力损失)
u2 gz + + = 常数 ρ 2 p
或
2 u12 p2 u2 gz1 + + = gz2 + + ρ 2 ρ 2
p1
p1
2 u12 p2 u2 + = + ρ 2 ρ 2
1.3.2 机械能守恒
(4)实际流体管流的机械能衡算 实际流体( μ ≠ 0,τ ≠ 0, 有阻力损失 )
2 ? u12 ? p2 ? u 2 ? gz1 + + ? ? + he = gz2 + + ? ? + hf ρ ? 2? ρ ? 2?
p1
2 u12 p2 u 2 gz1 + + + he = gz2 + + + hf ρ 2 ρ 2
p1
p1
2 p2 u2 u12 + + he = + + hf ρ 2 ρ 2
(1-42)
习惯上也把上式称为实际流体的柏努利方程或扩展了的柏努利方 程。
1.3.2 机械能守恒
(5)柏努利方程的应用 ①重力射流 ②压力射流 (6)柏努利方程的几何意义 以单位重量流体为衡算基准,有: 2 理想 p1 u12 p2 u 2 z1 + + = z2 + + ρg 2 ρg 2 实际流体( μ ≠ 0, 有阻力) 2 p1 u12 p2 u2 z1 + + + H e = z2 + + + Hf ρg 2 ρg 2 以单位体积位衡算基准,有:
2 p1 ρ u12 p2 ρ u2 ρ gz1 + + + Pt = ρ gz2 + + + ?Pf 2 2 ρg ρg
1.3.2 机械能守恒
注意①解题指南p140 教材 he hf He Hf
解题指南(包括本校编的试验讲义) We (J/Kg) ∑ Wf (J/Kg) he (m) ∑ hf (m)
注意②柏努利方程解题应注意的事项,截面、基准面的选取、压 强的表示方法。
1.3.3 动量守恒
有兴趣自学,一般了解。仅在阻力损失无法计算或 本身要求流体对壁面的作用力时才用动量守恒定律 解题。
1.4 流体流动的内部结构
本节的目的时为了了解流体流动的内部结构以便为阻 力损失计算打下基础。 1.4.1流体的形态 1.4.2湍流的基本特征 1.4.3边界层及边界层脱体(分离) 1.4.4圆管内流
体运动的数学描述
1.4.1 流体的形态
(1)两种流型——层流和湍流 (2)流型的判据——雷诺数Re
1.4.2 湍流的基本特征
(1)时均速度与脉动速度? ? 一般了解(自学) (2)湍流的强度和尺寸 ?
(3)湍流粘度 湍流时,动量传递不仅起因于分子运动,且来源于流体质点的横 向脉动,故不服从牛顿粘性定律,如仍希望用其形式,则:
τ = (μ + μ ' )
du x dy
(1-61)
1.4.3 边界层及边界层脱体(分离)
(1)边界层 ①流体在平板上流动是的边界层 ②管流时的边界层 (2)湍流时的层流内层和过渡层 不管是平板上的流动还是管内流动,若流体主体为湍流,都可分 为以下几个区域: 湍流区(远离壁面的湍流核心) 层流内层(靠近壁面附近一层很薄的流体层) 过渡层(在湍流区和层流区之间) (3)边界层的分离现象
1.4.4 圆管内流体运动的数学描述
(1)流体的力平衡 左端面的力 F1 = π r 2 p1 右端面的力 F2 = π r 2 p 2 外表面的剪切力 F = 2π rlτ 圆柱体的重力 Fg = π r 2l ρ g 因流体在均匀直管内作等速运动,各外力之和必为零, 即:
F1 ? F2 + Fg sin α ? F = 0
1.4.4 圆管内流体运动的数学描述
(2)剪应力分布 将 F1 、 F2 、Fg 、F 代入上式,并整理:
π r 2 p1 ? π r 2 p2 + π r 2l ρ g sin α ? 2π rlτ = 0 p1 ? p2 ( p1 + ρ gl sin α ) ? p2 τ= r= r
2l 2l
此式表示圆管中沿管截面上的剪应力分布。 剪应力分布与流动截面的几何形状有关,与流体种类、层流或湍 流无关,即对层流和湍流皆适用。
(2) 剪应力分布
τ ∝ r , r ↑,τ ↑; r = 0,τ = 0;
r = R时,τ = p1 ? p2 2l R,
其值最大。
1.4.4 圆管内流体运动的数学描述
(3)层流时的速度分布 层流时 τ 服从牛顿粘性定律:
du r dr dr dur p1 ? p2 τ = ?μ = r dr 2l
τ = ?μ
u r = ∫ du r = ?
0
ur
p1 ? p2 2l μ
∫
r
R
r dr =
p1 ? p2 2l μ
∫
R
r
rd r =
p1 ? p2 4μl
(R2 ? r 2 )
管中心r=0,
ur = umax =
所以
p1 ? p2 4μl
R2
r2 ur = umax (1 ? 2 ) R
1.4.4 圆管内流体运动的数学描述
(4)层流时的平均速度和动能校正系数 α
u =u= ∫
A
u r dA A
=
umax ∫
R
0
r2 (1 ? 2 )2π rdr R π R2
R
=
可得
2π umax π R2
? r2 r4 ? 1 ? 2 ? = umax ? 2 4R ? ?0 2
α =2
1.4.4 圆管内流体运动的数学描述
(5)湍流时的速度分布 层流 湍流
τ = ?μ
du r dr
dur dr dr
τ = ?( μ + μ ')
布不能像层流一样通过流体柱受力分析从理论上导出,只能将 试验结果用经验式表示:
μ ' 不是物性,其值与Re及流体质点位置有关,故湍流时速度分
r n ur = umax (1 ? ) R
(5)湍流时的速度分布
n与Re有关,在不同Re范围内取不同的值:
4 × 104 < Re < 1.1×105时,n = 1 6 1 7
1.1× 105 < Re < 3.2 × 106 时,
n = Re > 3.2 ×106 时,n = 1 10
不论n取1/6或1/10,湍流的速度分布可作如下推想:近管中心部分 剪应力不大而湍流粘度数值很大,由式(1-61)可知湍流核心处的 速度梯度必定很小。而在壁面附近很薄的层流内层中,剪应力相当 大且以分子粘度 μ 的作用为主;但 μ 的数值又远较湍流核心处 的 μ ' 为小,故此薄层中的速度梯度必定很大。图1-32表示湍流时的 速度分布。Re数愈大,近壁区以外的速度分布愈均匀。
(6)湍流时的平均速度及动能校正系数 α
1 取n = 积分:u = u = 0.817umax 7
u与umax 的关系与n有关
α ≈1
? u2 ? u2 ?u? 以后计算不论层流还是湍流均取 α = 1, ? ? = α ? ? = ? 2? 2 ?2? ? ?
2
1.5 阻力损失
1.5.1 两种阻力损失 1.5.2 湍流时直管阻力损失的试验研究方法——因次 分析法
1.5.1两种阻力损失
(1)直管阻力和局部阻力 hf (2)阻力损失表现为流体势能的降低 由式(1-42)
p1
2 p2 u2 u12 + + he = + + hf ρ 2 ρ 2
u (等径) he =0 (无外加机械能),1 =u2
hf = p1 ? p2
ρ
=(
p1
ρ
+ gz1 ) ? (
p2
ρ
+ gz2 )
阻力损失主要表现为流体势能的降低,既 ρ ;只有水平管道
?p z1 = z2 ),才能以 ?p 代替 ( ρ 表达 hf 。 ρ
?p
1.5.1两种阻力损失
(3)泛流时的直管阻力损失
p1 ? p2 2 p1 ? p2 ? d ? 2 1 u = umax = R = ? ? 2 8μ l 8μ l ? 2 ?
?p = p1 ? p2 =
?p
32 μ lu d2
(1-73)
32μ lu hf = = ρ ρd 2
1.5.2 湍流时直管阻力损失的试验研究方 法——因次分析法
(1)析因试验——寻找影响过程的主要因素(靠初步试验和经验)
hf = f (d , l , μ , ρ , u , ε )
(2)规划试验——减少试验工作量,试验结果易总结整理,有物 理意义。正交设计法,因次分析法等。 因次分析法将物理量因次抽出分析,将影响过程的物理量组 合成几个无因次的数群,数群的数目将少于自变量的数目,试验 工作量减少,但数群前的系数及各数群的指数因次分析法无法确 定,仍要靠试验确定,这种研究方法就是在绪论课中提到的半经 验半理论的研究方法。
1.5.2 湍流时直管阻力损失的试验研究方 法——因次分析法
因次分析法的基础是:任何物理方程的等式两边或方程中的没一 项均具有相同的因次,此称为因次和谐或因次一次性。从这一基 本点出发,任何物理方程都可以转化成无因次形式。 式(1-73)可以写成如下形式
hf l μ ( ) = 32( )( ) u2 d du ρ
(1-75)
式中没一项都为无因次项,称为无因次数群。 未作无因次处理前,层流时阻力的函数为: (1-76) hf = f ( d , l , μ , ρ , u ) 作无因次处理后,可写成
hf du ρ l ( ) = ?( , ) μ d u2
(1-77)
1.5.2 湍流时直管阻力损失的试验研究方 法——因次分析
法
对照式(1-74)与式(1-75),不难推测,湍流时的式(1-74) 也可写成如下的无因次形式
(
hf du ρ l ε ) = ?( , , ) μ d d u2
(1-78)
经变量组合和无因次化后,自变量数目由原来的6个减少到3个。 尤其重要的式,若按式(1-74)进行实验时,为改变 ρ和μ ,实 验中必须换多种液体;为改变d,必须改变实验装置。而应用因 次分析所得的式(1-78)指导实验时,要改变 du ρ 只需改变流 μ 速;要改变 (l / d ) ,只需改变测量段的距离,即两测压点的距离。 这是一个极为重要的特性,从而可以将水、空气等的实验结果推 广应用于其他流体,将小尺寸模型的实验结果应用于大型装置。
1.5.2 湍流时直管阻力损失的试验研究方 法——因次分析法
(3)数据处理——实验结果的正确表达 获得无因次数群后,各无因次数群之间的函数关系仍需由实验并经 分析去定。方法之一是将各无因次数群 (π 1、π 2、π 3……) 之间的函 数关系近似地用幂函数的形式表达 a b π 1=K π 2 π 3 (1-79) 此函数可线性化为 log π 1 = log K + a log π 2 + b log π 3 此后不难将 π 1、π 2、π 3 的实验值,用线性回归的方法求出系 数 K、a、b 的值,同时也检验了是(1-79)的函数形式是否适用。 对式(1-78)而言,根据经验,阻力损失与管长成正比,该式可改 写为 h l ε ( f ) = ? (Re, ) (1-81) u2 d d
1.5.3 直管阻力损失的计算式
由以上分析可知,直管阻力损失,无论式层流还是湍流,都与雷 诺数、速度的平方以及 l / d 有关。因此,我们可以将其写成以下 统一的表达式: (1)统一的表达式 l u2 J/Kg hf = λ d 2 l u2 或 Hf =λ J/N或m d 2g l ρu 2 ?p f = λ 或 J/m 3或Pa d 2
λ 是Re和相对粗糙度的函数,即
ε λ = ? (Re, )
d
1.5.3 直管阻力损失的计算式
(2)摩擦系数 ①层流 当 Re < 2000 时,流体在管内作层流流动,由式
64 l u 2 hf = Re d 2 可以得到 λ = 64 / Re 。
②湍流 当 Re > 4000 时,或流体作湍流流动时,前人通过大量 λ 的实验,得到了各种各样的 的关联式 如书上的式(1-85):
1
2ε 18.7 = 1.74 ? 2 log( + ) d Re λ λ
此式由于在等式的左、右两边都有,因此要用此式要进行迭代, 不方便。
1.5.3 直管阻力损失的计算式
下面我们介绍另外1个公式:
ε 68 λ = 0.1( + )0.23
d Re
ε 当流体在光滑管中运动时, / d 的影响可忽略,我们可以用
0.25 λ 柏拉修斯公式: = 0.3164 / Re 适用范围 Re = 5000 ~ 10000
顾毓珍公式:λ = 0.0056 +
0.500 6 适用范围 Re = 3000 ~ 3 × 10 Re0.32
1.5.3 直管阻力损失的计算式
(3) 摩擦因数图 64 λ= 前面学过的摩擦因数 λ ,除了层流时 R e 和光 0.3164 λ= 滑管的柏拉修斯公式 比较简单外,其余各公 R e 0.25 式都比较复杂,
用起来比较不方便。在工程计算中为 了避免试差,一般是将通过实验测出的 λ 与 R e 和 ε / d 的关系,以 ε / d为参变量,以 λ 为纵坐标,以 R e 为横坐标,标绘在双对数坐标纸上。如图1-34所示, 此图称为莫狄摩擦因数图。
1.5.3 直管阻力损失的计算式
1.5.3 直管阻力损失的计算式
由图可以看出,摩擦因数图可以分为以下五个区: ①层流区:R e ≤ 2000 , 与 ε / d 无关,与 R e 成直线关系,即 λ 64 。则流体的流动阻力损失与流速的关系为 λ=
Re
∑ p f1
l ρu 2 32μl =λ = 2 u∝u d 2 α
②过渡区。R e = 2000~ 4000 在此区内,流体的流型可能是层流,也可能是湍流,视外界 的条件而定,在管路计算时,为安全起见,对流动阻力的计算一 般将湍流时的 λ ~ R e 曲线延伸查取的 λ 数值。
1.5.3 直管阻力损失的计算式
③湍流粗糙管区 R e ≥ 4000 及虚线以下和光滑管λ ~ R e 曲线以上的区域。这个 ε λ = φ ( R e, ) 。由图中曲线分析可 区域内,管内流型为湍流,因此 d 知,当
ε
d
ε R λ 一定时, e ↑, ↓;当R e 一定时, ↑,↑。 λ
d
④湍流光滑管区 R e ≥ 4000 时的最下面一条 λ ~ R e 曲线。这是管内流型为湍流。
ε ≈ 0 ,因此 λ 与 ε 无关,而仅 由于光滑管表面凸起的高度很小,
d
5 λ 与 R e 有关。当 R e = 5000 ~ 1 × 10 时, =
0.3164 0.25 。 Re
1.5.3 直管阻力损失的计算式
⑤完全湍流区——阻力平方区 图中虚线以上的区域。此区域内 λ ~ R e 曲线近似为水平线,即 λ
?ε 有关, = φ ' ? ? 。这是由于 R e 增加至这一 λ ? d d? ? 区域,层流底层厚度 δ b ε ,凸出的部分都伸到湍流主体中, 质点的碰 撞更加剧烈,时流体中的粘性力已不起作用。固包括 μ 的 R e 不再影响 λ 的大小。此时压力降(阻力损失)完全由惯性
与 R e 无关,只于
ε
力造成的。我们把它称为完全湍流区。对于一定的管道, 为定 d 2 l ρu ?p f = λ ∝ u 2。所以完全湍流区又 值, =常数,由范宁公式 λ
ε
ε 称阻力平方区。由图可知, ↑,达到阻力平方区的 R e↓ d
d 2
1.5.3 直管阻力损失的计算式
⑷粗糙度对 λ 的影响
ε? ? λ = φ ? R e, ? 可以看出,除流型对 λ 有影响外,管壁的粗糙度ε 由
? d?
对 λ 也有影响,但其影响因流型不同而异。 流体输送用的管道,按其材料的性质和加工情况大致可以分为二类: 光滑管:玻璃管、黄铜管、塑料管 粗糙管:钢管、铸铁管、水泥管
1.5.3 直管阻力损失的计算式
管壁粗糙度可用:绝对粗糙度 ε ( ε 指壁面凸出部分的平均高度) ε 相对粗糙度
d
ε 相同的管道,直径 d 不同,对 λ 的影响就不同。故一般用相对
粗糙度
ε
d
来考虑对 λ 的影响。
①层流:层流时,管壁上凹凸不平的地方都被有规则的流体层所覆 盖,而流速又比较缓慢,流体质点对管壁凸出部分不会有碰撞作用, ε 所以层流时 与 λ 无关,粗糙度的大小并未改变层流的速度分布和 内摩擦规律。
1.5.3 直管阻力损失的计算式
②湍流时,前面我们已知道,湍流时靠管壁处总是存在一层层流 λ 内层,其厚度设为 δ b ,若δ b > ε ,则此时管壁粗糙度对 的影响 与层流相近,若 δ b < ε 则管壁突出部分便伸入湍流区与流体质点 R 发生碰撞,便湍流加剧,此时 对λ 的影响便成的主要因素。 e ε 越大,层流内层越薄,这种影响越显著。当 R e 增大到一定程度, 层流内层薄得使表面得凸出完全暴露在湍流区内,则在增大R e , 只要ε 一定, 就一定了,此时就进入了阻力平方区,即阻力损失 λ 2 与 u 成正比:h f ∝ u 2 。
1.5.3 直管阻力损失的计算式
⑸实际管得当量粗糙度 管壁粗糙度对阻力系数 λ 的影响首先是在人工粗糙管中测定得。 人工粗糙管是将大小相同得砂粒均匀地粘着在普通管壁上,认为 地造成粗糙度,因而其粗糙度可以精确测定。工业管道内壁得凸 出物形状不同,高度也参差不齐,粗糙度无法精确测定。实践上 通过试验测得阻力损失并计算λ 值,然后由图1-34反求处相当得 相对粗糙度,称为实际管道得当量相对粗糙度。由当量相对粗糙 度可以求出当量得绝对粗糙度 ε 。
1.5.3 直管阻力损失的计算式
⑹非圆形管得当量直径 前面讨论得都是圆形管道。在工业生产中经常会遇到非圆形截面 得管道或设备。如套管换热器环隙,列管换热器管间,长方形得 通分管等。对于非圆形管内的流体流动,必须找到一个与直径 d 相当的量,使 R e 、h f 等才有可能进行计算,为此类似当量粗糙 度引入当量直径的概念,以表示非圆形管相当与直径为多少的圆 形管。当量直径用 d e 表示 我们来一下圆管的直径: πd 2 l 内径为 d ,长为 l ,其内部可供流体流过的体积为 4 ,其被润 湿的内表面积为 πdl ,因此有下列关系:
π 2 πd 2 d l 流通截面积 d = 4× 4 = 4 4 = 4× πdl πd 润湿周边长
1.5.3 直管阻力损失的计算式
对非圆形管:可以类比上式而得到其当量直径为:
d = 4× 流通截面积 润湿周边长
对长 a ,宽 b 为的矩形管道
d e = 4× ab 2(a + b )
当 a : b > 3 时,此式误差比较大。 对于外管内径为 d ,内管外径为d 2 的套管环隙
π 2 2 d1 ? d 2 d e = 4× 4 = d1 ? d 2 π (d 1 ? d 2 )
(
)
1.5.3 直管阻力损失的计算式
当量直径的定义是经验性的,并无充分的理论依据。将求阻力损 失中的 d 改成 d e 即可求;但对于层流流动图1-34中的层流摩擦 因数图不可用。因
为查图得到的λ 不可靠。可用下式求λ
λ=
C d e uρ ,Re = Re μ
套管环隙。 C = 96 正方形截面。 C = 57 b 1 62 长为 a ,宽为 b 的矩形截面: = 时, C = ;
a 2 b 1 = 时, C = 。 73 a 4
u 注:非圆形管道的截面积不能用 d e 求,还有qV , 也不能用d e 求
1.5.4局部阻力的损失
化工管路中的管件种类繁多,常见的管件如表1-2所示。流体 流 过各种管件都会产生阻力损失。和直管阻力的沿程均匀分布不 同,这种阻力损失是由管件内的流道多变所造成,因而称为局部 阻力损失。局部阻力损失是由于流道的急剧变化使流动边界层分 离,所产生的大量漩涡,使流体质点运动受到干扰,因此即使流 体在直管内是层流流动,但当它通过管件或阀门时也是很容易变 成湍流。 ⑴突然扩大与突然缩小 ⑵局部阻力损失的计算
1.5.4局部阻力的损失
⑴突然扩大与突然缩小 ①突然扩大 ξ e 流体流过如图所示的突然扩大管道时,由于流股离开壁面成一 射流注入了扩大的截面中,然后才扩张道充满整个截面。由于流 道突然扩大,下游压强上升,流体在逆压强梯度下流动,射流与 壁面间出现边界层分离,产生漩涡,因此有能量损失。 ②突然缩小 ξ e 突然缩小时,流体在顺压强梯度下流动,不致于发生边界层脱 离现象,因此在收缩部分不会发生明显的阻力损失。但流体有惯 性,流道将继续收缩至A-A面后又扩大。这时,流体在逆压强梯度 下流动,也就产生了边界层分离和漩涡。因此也就产生了机械能 损失,由此可见,突然缩小造成的阻力主要还在于突然扩大。
1.5.4局部阻力的损失
1.5.4局部阻力的损失
⑵局部阻力损失的计算 在湍流情况下,为克服局部阻力所引起的能量损失,是一个 复杂的问题,而且管件种类繁多,规格不一,难于精确计算。通常 要用以下两种方法: ①阻力系数法 u2 近似地将克服局部阻力引起的能量损失表示成动能 2 的一个倍 数。这个倍数称为局部阻力系数,用符号 ξ 表示,即
u2 hf = ξ 2
'
(J/Kg)
2
? A ? ξ e = ?1 ? 1 ? 突然扩大的阻力系数可从表1-2查得,也可用式 ? A ? 2 ? ?
? ?
来求。
A ?
2
突然缩小的阻力系数也可从表1-2查得,也可用式ξ e = 0.5?1 ? A1 ? 来求。 ? ?
?
1.5.4 局部阻力的损失
下面有两种极端情况: 流体自管出口进入容器,可看作很小的截面突然扩大道很大的截 面,相当于突然扩大时
A1 ≈0 A2
u2 u2 h 的情况,故管出口ξ 0 = 1,f = ξ 0 = 2 2
'
流体自容器流进管的入口,是自很大的截面突然缩小到很小的截
u ' A h 面,相当于突然缩小时 2 ≈ 0 的情况,故管入口ξ i = 0.5 , f = 0.5 2 A1
2
1.5.4局部阻力的损失
②当量长度法 把流体流
过某一管件或阀门的局部阻力折算成相当于流过一 段与它直径相同,长度为l e 的直管阻力。所折算的直管长度称为 该管件或阀门的当量长度,以 le 表示,单位为m。那么局部阻力损
le u 2 失为: f = λ ,见图1-38管件和阀门的当量长度的共线图。 h d 2
'
如闸阀1/2关时,管径为60mm时的当量长度,由图上得 le = 13.5 。 注:上述求局部阻力中的速度 u 是用小管截面的平均速度。
1.5.4局部阻力的损失
显然,上述两种方法在计算局部阻力时,由于与定义不同,从而 使两种计算方法所得的结果不会一致,它们都是工程计算中的近 似估算值。 由此,管路的总阻力损失的直管阻力损失与局部阻力损失之和, 2 即 l u2 u2 ? l ?u ' ∑ h f = h f +h f = λ d 2 + ∑ ξ 2 = ? λ d + ∑ξ ? 2
? ?
或
l u2 ∑ le u 2 = λ l + ∑ le u 2 ∑ h f = h f +h f = λ d 2 + λ d 2 d 2 有时,由于le 或 ξ 的数据不全,可将两者结合起来混合应用,即
'
? l + ∑ le ? u2 ∑ h f = ? λ d + ∑ξ ? 2 ? ? ? ?
当管路由若干直径不同的管段组成是,由于各段的流速不同, 此时管路的总能量损失应分段计算,然后再求和。
1.6 流体输送管路的计算
前面几节我们已导出了连续性方程式,机械能衡算式以及阻力 损失的计算式。据此,可以进行不可压缩流体输送管路的计算。 化工管路按其布置情况可分为简单管路与复杂管路两种,下面 我们分别讨论其计算方法。 1.6.1简单管路计算 1.6.2复杂管路计算
1.6.1简单管路计算
简单管路是指灭有分支或汇合的单一管路。在实际计算中碰到的 有三种情况:一是管径不变的单一管路;二是不同管径的管道串 联组成的单一管路;三是循环管路。 在简单管路计算中,实际是连续性方程,机械能衡算式和阻力损 失计算式的具体运用。即联立求解这些方程:
?d ? u q S = d 2 u或 2 = ? 1 ? 连续性方程: 4 u1 ? d 2 ? ? ?
π
2
机械能衡算式:
2 u12 p2 u2 gz1 + + + we = gz 2 + + + Σ hf ρ 2 ρ 2
p1
ε 摩擦系数计算式(或图): λ = φ ? Re , ? ? ?
? d?
1.6.1简单管路计算
下面我们先分析一下管径不变的简单管路计算 ⑴等径管路计算 如图所示为一管径不变的管路。当被输送的流体已定,其物性 μ , ρ 已定,上面给出的三个方程中已包含有9个变即qv , d , u, p1 , p2 , λ , l , Σζ (或 Σl e )从数学上知道,需给定6独立变量,才能解出3个未知 量。由于已知量与未知量情况不同,因而计算的方法有所不同。 工程计算中按管路计算的目的可分为设计型计算与操作型计算两 类。
1.6.1简单管路计算
①简单管路的设计型计算 设计型计算是给定输送任务,要求设计经济上合理的管路。 典型的设计型
命题如下: 设计要求:为完成一定量的流体输送任务 qv ,需设计经济上合理 的管道尺寸(一般指管径 d )及供液点所提供的势能 ? p1 ? 。 ? ? ? ?
? ρ?
q ε 给定条件: v 、l 、 ρ (需液点的势能)、管道材料及管道配件、 、 Σζ (或 Σle ) 等5个量。
在以上命题中只给定了5个变量,上述三个方程求4个未知量 仍无定解。要使问题有定解,还需设计者另外补充一个条件,这 是设计型问题的主要特点。
p2
1.6.1简单管路计算
u 对以上命题剩下的4个待求量是:、d、λ、 1 。工程上往往是 ρ p1 通过选择一流速 u ,继而通过上述方程组达到确定 d 与 ρ 的目的。 p1 由于不同的 u 对应一组不同的 d 、 ρ ,设计者的任务在于选择一 组经济上最合适的数据,即设计计算存在变量优化的问题。什么 样的数据才是最合适的呢? qv, d与 1 成反比, ↑, ↓,设备费用↓,但 ↑ u 对一定 d u u2 使流动阻力↑,操作费用↑;反之, ↓, ↑,设备费用↑,但 d u u uopt ↓使流动阻力↓,操作费用↓。因此,必存在一最佳流速 , 使输送系统的总费用(设备费用+操作费用)最小。原则上说可 以通过将总费用作为目标函数,通过取目标函数的最小值来求出 最优管径(或流速),但对于车间内部规模较小的管路设计问题, 往往采取P50,表1-3列出经验流速以确定管径再根据管道标准进 行调整。 p
1.6.1简单管路计算
注:再选择流速时,应考虑流体的性质。粘度较大的 流体(如油类)流速应取得低;含有固体悬浮物的流 体,为了防止管路的堵塞,流速不能取得太低。密度 较大的液体,流速应取得低,而密度小的液体,流速 则可取得壁液体大的多。气体输送中,容易获得压强 的气体,流速可以取高些;而一般气体输送的压强不 易获得,流速不宜取太高。还有对于真空管路,流速 的选择必须保证产生的压降 ?p 低于允许值。管径的选 择也要受到结构上的限制,如支撑再跨距5m以上的普 通钢管,管径不应小于40mm。
1.6.1简单管路计算
例10-11 钢管总长为100m,200C的水在其中的流率为27m3/ h。输送 过程中允许摩擦阻力为40J/ kg,试确定管路的直径。
d 解:本题为简单管路的设计型计算问题,待求量为管径 。由于 d u 未知,即使 Vs 已知, 也无法求, Re 无法计算, λ 不能确定,故 须用试差法计算。根据题给条件,有
2 ?3 3 将 Σwf = 40 J/kg 、l = 100 m 、u = Vs / (0.785 d )、Vs = 27 / 3600 = 7.5 × 10 m /s 代入上式并整理,得
l u2 Σwf = λ d 2
d = 0.163λ
1 5
(a )
例10-11
μ 20 0C水的密度ρ 为1000kg/ m3,粘度 为1.005cP(200C水的粘度 是一个很特殊的数据,许多出题者不会将200C水的 μ 作为
已知条件 给出,读者必须记住,近似计算可将其取为1cP)。把已知数据代 入 Re表达式,得
7.5 × 10 ?3 × 1000 9507 Re = = = = μ d 0.785d 2 μ 0.785 × 1.005 × 10 ?3 d dup dVs ρ
(b)
粗糙管湍流时 λ 可用下式计算
? e 68 ? λ = 0.1? + ? ? d Re?
0.23
(c)
本题取管壁绝对粗糙度 e = 0.2mm = 0.2×10-3m,湍流时λ 值约在 0.02 ~ 0.03左右,故易于假设λ 值,而管径 d 的变化范围较大,不易 假设。本题设初值λ =0.028,由式(a)求出 d,再由式(b)求出R e , 计算相对粗糙度 e / d ,把 e / d 及R e 值代入式(c)求 λ ′ ,比较 λ ′ 与初设 入,若两者不符,则将 λ ′ 作为下一轮迭代的初值,重复上述步骤, 直至 λ ′ ? λ ≤ 0.001为止。表10-1为迭代结果。
例10-11
表10-1 例10-11计算结果
λ
0.028 0.0264
d /m
Re
1.192×105 1.207×105
e/d
2.51×10-
3
λ′
0.0264 0.0265
λ′ ? λ
0.0018 0.001
0.0797 0.0788
2.54×10-
3 经过两轮迭代即收敛,故计算的管道内径 d 为0.0788m,实际上市 场上没有此规格的管子,必须根据教材附录提供的管子规格选用 合适的标准管。本题输送水,题目没有给出水压值,故认为水压 不会太高,根据教材提供的有缝钢管(即水、煤气管,最高承受 压力可达16kgf/cm2)规格,选用 φ 3′′ 普通水、煤气管,其具体尺寸 为 φ 88.5 × 4 mm ,内径 d = 88.5 ? 2 × 4 = 80.5 mm = 0.0805 m 。
例10-11
由于所选与计算不一致,必须验算采用此管时的摩擦阻力是否超过允许值。
u= Vs (27 / 3600) = 1.47 m/s = 0.785d 2 0.785 × 0.08052
Re =
duρ
μ
=
0.0805 × 1.47 × 1000 = 1.177 × 10 5 ?3 1.005 × 10
e 0.2 × 10 ?3 = = 2.48 × 10 ?3 d 0.0805
? e 68 ? λ = 0.1? + ? ? d Re?
0.23
68 ? ? = 0.1 × ? 2.48 × 10 ?3 + ? 1.177 × 10 5 ? ?
0.23
= 0.0264
l u2 100 1.47 2 Σwf = λ = 0.0264 × × = 35.4 J/kg < 40 J/kg d 2 0.0805 2 计算结果说明,采用φ 3′′ 水、煤气管时的摩擦阻力小于允许值40
J/ kg,故认为所选的管子合适。
1.6.1简单管路计算
②简单管路的操作型计算 操作型计算问题是管路已定,要求核算在某给定条件下管路 的输送能力或某项技术指标。这类问题的命题如下: p p d、l、Σζ (或Σl e )、ε、 1 、 2 等6个量; 给定条件: ρ ρ qv; 计算目的:求输送量 或 p d、l、Σζ (或Σl e )、ε、 1 、q v 等6个量; 给定条件: ρ p2 计算目的: ρ 计算的目的不同,命题中须给定的条件亦不同。但是,在各种 操作型问题中,有一点是完全一致的,即都给定了6个变量,方程 u 组有唯一解。在第一种命题中,由于 未知, R e 未知,无法确定 流型, λ = ? 不知道,必须用试差法求解。
1.6.1简单管路计算
先假设 或 u ( 变化范围比 u 变化范围小,先假设λ 求解比较 λ λ 方便,
因为一般情况下 λ = 0.02 ~ 0.03 );通常可取进入阻力平方 区的 λ 作为初值。 假设λ或u → qv或u → Re → 确定流型 → λ → 与假设值比较 ,若λ ≠ 假设 λ , λ 则重新假设λ 进行试差计算直至λ = 假设 。 若已知阻力损失服从平方或一次方定律时,则可以解析求解,无
λ 需试差。(如层流, =
64 )。 Re
讲了这么多简单管路的操作型计算,下面我们通过两个例子 来说明。
1.6.1简单管路计算
例10-8 粘度为30cP,密度为900kg/m3的液体,自A经内径为40mm的管 路进入B,两容器均为敝口,液面视为不变。管路中有一阀门,当 阀全关时,阀前后压力表读数分别为0.9at和0.45at,现将阀门打 至1/4开度,阀门阻力的当量长度为30m,阀前管长50m,阀后管长 20m(均包括局部阻力的当量长度,试求: (1)管路的流量m3/h? (2)阀前后压力表读数有何变化?
例10-9 如例10-8附图所示,高位槽A内的液体通过一等径管流向槽B。 在管线上装有有阀门,阀前、后1、2处分别安装压力表。假设槽A、 B液面维持不变,阀前、后管长分别为、。现将阀门关小,试分析 管内流量及1、2处压力表读数如何变化。
1.6.1简单管路计算
⑵串联管路 由不同直径的管道串联组成的不等径管路。如图: 对于不可压缩流体,由连续性方程得,其流过串联管路内各段得体积流 量相等。 q v1 = q v 2 = q v 3 (不可压缩流体)
π
4
d1 u1 =
2
π
4
d 2 u2 =
2
2
π
4
d 3 u3
2
2
?d ? ∴ u 2 = u1 ? 1 ? ?d ? ? 2?
?d ? u3 = u1 ? 1 ? ?d ? ? 3?
串联管路的阻力损失等于各段管路阻力损失之和,即
∑ h f = ∑ h f 1 +∑ h f 2 + ∑ h f 3
2 2 l u l 1 u1 l2 u2 = λ1 + (λ2 + ξ2 ) + (λ3 3 + ξ 3 ) 3 d1 2 d2 2 d3 2 2
1.6.1简单管路计算
⑶循环管路的计算 如图所示,循环管路,在管路中任取一截面同时作为上游1-1`截 面和下游2-2`截面,则 z1 = z 2 , u1 = u2 , p1 = p2 ,机械能衡算式化为:
he = ∑ h f
上式说明,对循环管路,外加的能量全部用于克服流动阻力, 这是循环管路的特点,后面解题时常用到。 由以上分析我们可以看出:对于简单管路,通过各管段的质 量流量相等,对于不可压缩流体,体积流量相等;整个管路的阻 力损失等于各管段阻力损失之和。
1.6.1简单管路计算
1.6.2复杂管路计算
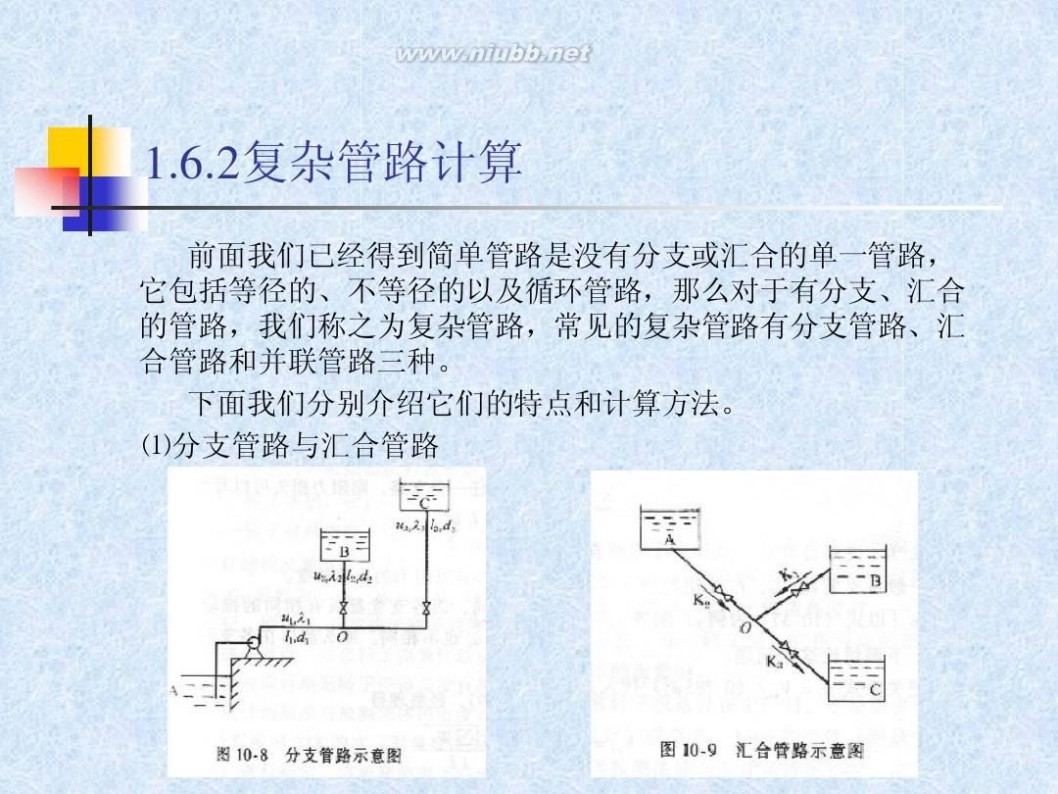
前面我们已经得到简单管路是没有分支或汇合的单一管路, 它包括等径的、不等径的以及循环管路,那么对于有分支、汇合 的管路,我们称之为复杂管路,常见的复杂管路有分支管路、汇 合管路和并联管路三种。 下面我们分别介绍它们的特点和计算方法。 ⑴分支管路与汇合管路
1.6.2复杂管路计算
特点: ①流量 由上图分支或汇合管路,我们可以看
出,不管是 分支管路还是汇合管路,对于稳态流动,他们的流量 关系为:
qVA = qVB + qVC
π
4
2 d Au A =
π
4
2 d BuB +
π
4
2 d C uC
即总管流量等于各支管流量之和
1.6.2复杂管路计算
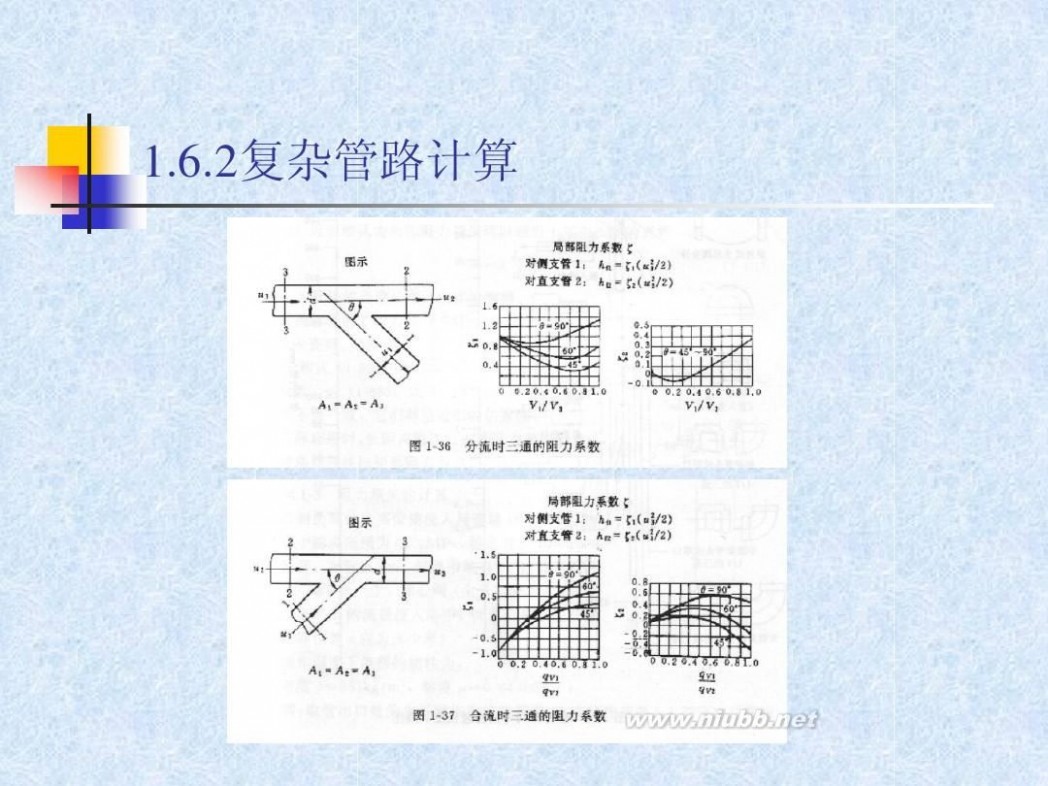
②分支点或汇合点O处的总机械能 EO 不管是分支还是汇合,在交点O处都存在有能量交换与损失。 如果弄清楚O点处的能量损失及交换,那么前面讲到的对于单 一管路机械能衡算式同样可以用于分支或汇合管路,工程上采用两 种方法解决交点处的能量交换和损失。 A.交点O处的能量交换和损失与各流股流向和流速大小都有 关系,可将单位质量流体跨越交点的能量变化看作流出管件(三通) 的局部阻力损失,由实验测定在不同情况下三通的局部阻力系数 。 ε0 ε0 当流过交点时能量有所增加,则 值为负,能量减少,则为正。见 图1-36,1-37,只要各流股的流向明确,仍可跨越交点列出机械能 衡算式。 B.若输送管路的其他部分的阻力较大,如对于ε / d 大于1000 的长管,三通阻力所占的比例很小,而可以忽略,可不计三通阻力 而跨越交点,列出机械能衡算式。
1.6.2复杂管路计算
1.6.2复杂管路计算
对于图所示分支管路,我们对其列机械能衡算式可得
2 p u uA gz A + + + he = gzO + O + O + ∑ h fA~O ρ 2 ρ 2 2 2 pO u O pB u B EO = gzO + + = gz B + + + ∑ h fOB ρ 2 ρ 2 2 pC u C = gzC + + + ∑ h fOC 2 ρ
pA
2
即对于分支或汇合管路,无论各支管内的流量是否相等,在分支 点O或汇合点处的总机械能 EO 为定值。
u gz A + + A + he = EO + ∑ h fA?O ρ 2 2 pB u B = gz B + + + ∑ h fAO + ∑ h fOB ρ 2
u = gzC + + C + ∑ h fAO + ∑ h fOC ρ 2 pC
2
pA
2
1.6.2复杂管路计算
分支管路所需的外加能量 he可根据上式,不同的分支算出的结果 不一样,我们应该取哪一个呢? 应该由远到近,分别求出满足各支管输送要求的 he ,然后加以比 较,取其中最大的 he 作为确定输送机械功率 N 的依据。这样确定的 对需要能量较小的支路而言太大,此时可通过该支路上的阀门进行 调节,让多余的能量消耗在阀门上。 若分支管路AO间没有泵,则式中he =O。由高位槽A向B、C两 个设备送液就属于这种情况,此时所需的高位槽的液面高度 z (或 A p A )亦按输送要求高的支路确定。
1.6.2复杂管路计算
对汇合管路,同样可以根据汇合点的总机械能的 定值进行分析。即对于图示汇合管路
uA gz A + + = EO + ∑ h fA?O ρ 2
u gz B + + B = EO + ∑ h fB ?O ρ 2 pB
2
pA
2
uC EO = gzC + + + ∑ h fC ?O 2 ρ
pC
2
1.6.2复杂管路计算
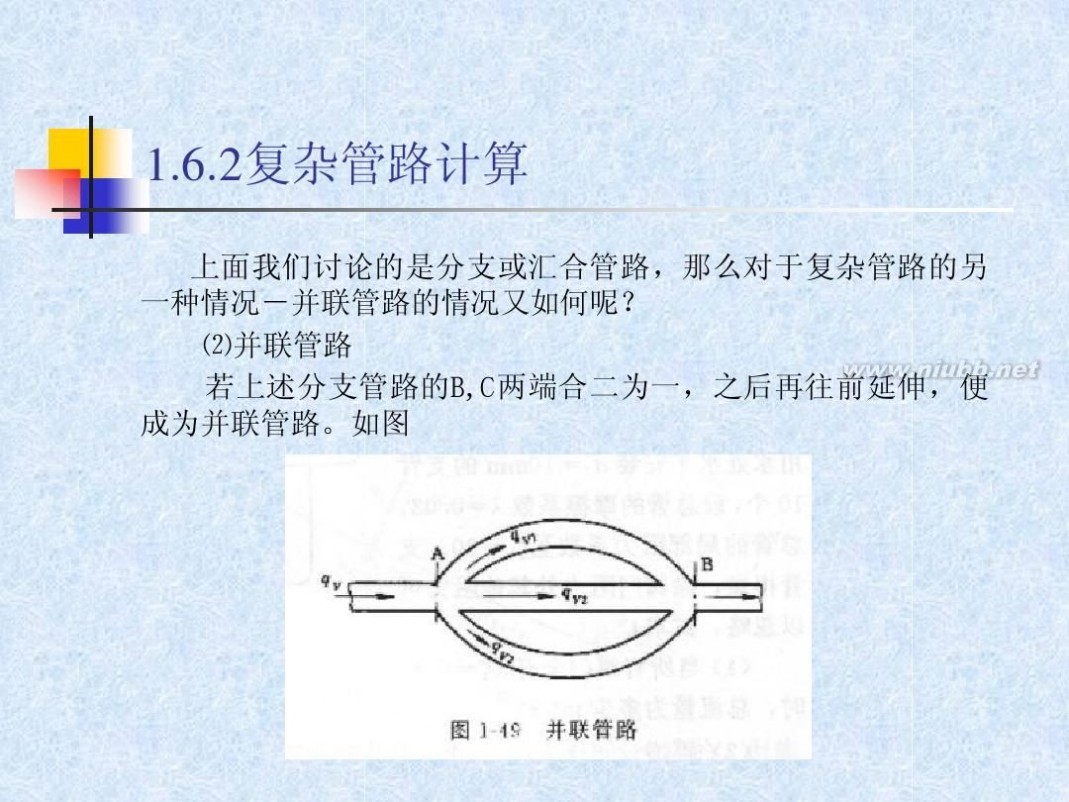
上面我们讨论的是分支或汇合管路,那么对于复杂管路的另 一种情况-并联管路的情况又如何呢? ⑵并联管路 若上述分支管路的B,C两端合二为一,之后再往前
延伸,便 成为并联管路。如图
1.6.2复杂管路计算
特点: ①主管的流量等于各支管流量之和。 qV = qV 1 + qV 2 + qV 3 或 ②各支管的阻力损失相等。 各支管的阻力损失:在分流点O和汇合点Q处两截面可以列机 械能衡算式得 2 2
gz O +
2 2 d 2u = d12u1 + d 2 u 2 + d 3 u3
O →1→ Q
O →2→ Q
O→3→Q
ρ p gzO + O ρ p gz O + O ρ p gz O + O ρ
pO
+
uO 2 2 uO + 2 2 uO + 2 2 uO + 2
= gz Q +
pQ
ρ 2 2 pQ u Q = gzQ + + + Σhf 1 ρ 2 2 pQ u Q = gz Q + + + Σhf 2 ρ 2 2 pQ u Q = gz Q + + + Σhf 3 ρ 2
+
uQ
+ ΣhfOQ
1.6.2复杂管路计算
比较上面三式可知:
ΣhfO = Σhf 1 = Σhf 2 = Σhf 3
= g (zO ? zQ ) + PO ? PQ +
2 2 uO ? uQ
ρ
2
=
PO ? PQ
ρ
+
2 2 uO ? uQ
2
即并联管路各支管阻力损失相等,这是并联管路得主要特征。 即单位质量流体从 O → Q ,不论通过哪一支管,阻力损失应是相 等的。 若O、Q点在同一水平面上,且O、Q处管径相等,则
Σhf 1 = Σhf 2 = Σhf 3 = pO ? pQ
ρ
并联管路各支管流动阻力损失相等,那么各支路得流量是否 相等呢?或者说各支路流量得关系又如何?与什么有关?
1.6.2复杂管路计算
如果并联管路中有 n 个支路,各管段得阻力损失可以写为:
li ui2 Σhf i = λi di 2
式中 li 包括局部阻力的当量长度。 一般情况各支管的长度、直径及粗糙度是不相同的,但各支 管的流体流动的推动力 ?p 是相同的,因此各支管的流速也不同。 那么流体在各支管中如何分配呢?将 ui = qvi / (0.785d i2 )代入上式并经 整理得
qVi =
π 2
4
d i5 Σhfi
λi li
1.6.2复杂管路计算
因为Σhf i 相等,所以可以得到各支管流量分配的关系式:
qV 1 : qV 2 : LL : qVn =
5 5 dn d15 d2 : : LL : λ1l1 λ2 l 2 λn l n
同时应满足: qV = qV 1 + qV 2 + LL + qVn λ 如果总流量 qV 、各支管的 li 、 i 、d i 均已知,由以上两式即 可联立求出qV 1 、qV 2 、…… qVn 求出O,Q两点间的阻力损失 ΣhOQ 。 如果考虑 λi 的变化,那么上述问题可能需要试差或迭代求 解。
li ui2 。选任一支管用即可 Σhf i = λi di 2
1.6.2复杂管路计算
复杂管路计算的注意事项: ①在设计计算分支管路所需能量时,为了保证将流体输送至需 用能量最大的支管,就需要按照耗用能量最大的那支管路计算。 通常是从最远的支管开始,有远及近,依次进行各支管的计算。 如在按已知的流量和管路(管路上阀门全开)计算出的能量不等 时,应取能量最大者为依据。 ②在计算管路的总阻力时,如果管路上有并联管路存在,则 总阻力损失应为主管部分与并联部分的串联阻力损失。在计算并 联管路的阻力时,只需考虑其中任一管段的阻力即可,绝不能将 并联的各段阻力全部加在一起,以作为并联管路的阻力。
1.6.3可压
三 : 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程


流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程
流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

流体力学教材 流体力学经典教程

四 : 工程流体力学考试重点50

1. 2.
质量力:质量力是作用于每一流体质点(或微团)上的力,与体积或质量成正比。 表面力:表面力是作用在所考虑的流体表面上的力,且与流体的表面积大小成正比。外界通过接触传递,与表面积成正比的力。 3.
当不计温度效应,压强的变化引起流体体积和密度的变化,称为流体的压缩性。当流体受热时,体积膨胀,密度减小的性质,称为流体的热胀性。 4.
单位压强所引起的体积变化率(压缩系数
正值,而相对压强p则可正可负。
p?p?pa,绝对压强和相对压强之差是一个当地大气压pa。
'
强近似按静压分布即为常数。
z?
p
?
?C,C
30. 急变流是流速的大小和方向沿程急剧改变的
流动,其特征是流线间夹角很大或曲率半径较小或二者兼而有之,流线是曲线,过水断面不是一个平面。
31. 根据流场中各运动要素与空间坐标的关系,
流体运动又分为一维流动、二维流动和三维流动。若流体的运动要素是三个空间坐标和时间t的函数,这种流动称为三维流动。若只是两个空间坐标和时间t的函数,就称为二维流动。若仅是一个空间坐标和时间t的函数,则称为一维流动。
32. 流束:过流体中任一过流断面上各点作流线,
则得到充满流管的一束流线簇,称为流束。在流束中与各流线相铝直的横截面称为过流断面。
33. (1)有压流动:总流的全部边界受固体边界
的约束,即流体完全充满流道的流动;(2)无压流动:总流边界的一部分受固体边界约束,另一部分与气体或空气接触,流体有自由液面的流动;(3)射流:总流边界不受固体边界约束,液流完全与气体或空气接触,形成自由液面的流动。
34. 流量是指单位时间内通过渠道、管道等某一
过流断面的通量。体积流量:
17. 压强的三种度量单位:1)用单位面积上的力
来表示,即应力单位。以压强的基本定义出发:Pa(N/m);2)以大气压的倍数表示。以大气压来表示:标准大气压 atm温度为0℃,海平面上的压强,即101.325kPa。工程大气压 at 海拔200米处的正常大气压
5. 6.
1at=1kgf/cm2,1kgf=9.8N;3)以液柱高度
1dV
)。?表示压强。以液柱表示:mH2O,mmH2O或mmHg。 ?p??p?越容易
Vdp压缩18. PX??gh CAX?pCAXdpdp。
E??P??V??,?P??液体作用在柱面上水静压力的水平分力,其E?
dVd?。 大小等于作用在该柱面在铅垂平面的投影面
单位温度所引起的体积变化率(体积热胀系上的水静压力。水平分力的作用线通过投影
1dV
数?V?)。 面积的压强中心,方向指向柱面。hC为平
VdT黏性是流体抵抗剪切变形的一种属性。当流面AX形心C处的淹没深度。
体内部的质点间或流层间发生相对运动时,19. PZ??gVP 液体作用在柱面上水产生切向阻力(摩擦力)抵抗其相对运动的特性,称作流体的黏性。流体的黏性是流体
静压力的铅直分力等于压力体内液体的重量。 20.
与
7.
8. 9.
duF??Adudy 其中F——内摩擦力,N;——法向速度梯度,即在与流
dyy方向流体速度的变化率,体方向相互垂直的
1/s;?——比例系数,称为流体的黏度或动力黏度,Pa?s。
du
??? 表明流体层间的内摩擦力
dy或切应力与法向速度梯度成正比。
产生流动阻力的根源。
液体的黏度随温度升高而减小,气体的黏度则随温度升高而增大。液体主要是内聚力,气体主要是热运动。温度间距
P?P?P
水
平
线
2
X2
Z 合力P的作用线
夹
角
为
:
??arctan(PZ/PX)
的
21. 压力体:
实压力体:压力体abc包含液体体积,垂直分力方向垂直向下。虚压力体:压力体abc不包含液体体积,垂直分力方向垂直向上。
22. 描述流体运动的两种方法:1)拉格朗日法:
是以流场中每一流体质点作为描述对象的方法,它以流体个别质点随时间的运动为基础,通过综合足够多的质点运动而获得整个流动规律。2)欧拉法;是以流体质点流经流场中各空间点的运动即以流场作为描述对象研究
35. 36.
10. 11.
12.
13.
14.
?1??2,则v1A1?v2A2。 ?u?u?u?ua??u?v?w三大模型:1)连续介质模型;2)不可压缩 分流: xQ1?Q2?Q3?t?x?y?z流体模型;3)理想流体模型。 ,
vA?vA?vA当把流体看作是连续介质后,表征流体性质23. 欧拉法度 1汇流:1 2233?v加速?v表达?v式:?v38.Q1?Q2?Q3
ay??u?v?w,的密度、速度、压强和温度等物理量在流体
?t?x?y?z39.vA3中也应该是连续分布的。优点:可将流体的,加速度由两部分组成:第一部分是由于某 1A恒定总流的能量方程:1)理想流体恒定元流1?v2A2?v3
2各物理量看作是空间坐标和时间的连续函一空间点上的流体质点的速度随时间的变化的能
p1量u12方程p2:u2?w?w?w?w数,从而可以引用连续函数的解析方法等数z1???z2??az???wvu?v2?2g?2g,,;第二部分是某学工具来研究流体的平衡和运动规律。 速度,t?y?z。单位重量理想元流的能量方程式一般表达
pu?t?t?t流体静压强的特性:1)流体静压强的方向垂一瞬时由于流体质点的速度随空间点的变化式为:z???C。物理意?2g直指向受压面或沿作用面的内法线方向;2)而引起的,称为迁移加速度,又称为位变加义:z表示单位重量流体所具有的位置势能
?u?u?up,v,w,当地加平衡流体中任意一点流体静压强的大小与作速度,u(简称位能)表示单位重量流体所具有
p?x?y?z?用面的方位无关,只与点的空间位置有关。 速度和迁移加速度之和称为总加速度。 的压强势能(简称压能),z?表示单
1?p1?p1?pX??0,Y??0,Z24.? ?0位重量流体所具有的总势能,表示单
??x??y?动时空间点上各运动要素均不随时间而变化?z2g。位重量流体2所具有的动能,
pu
dp??(Xdx?Ydy?Zdz)的流动。 表示单位重量流体所具z??
?2g全微分方程。 25. 非恒定流:又称非定常流,是指流场中的流有的总机械能。几何意义:z表示位置水头,pp2在平衡流体中,压强相等的各点所组成的面体流动空间点上各水力运动要素随时间的变表示压强水头,z?u?表示测压管
2?称为等压面。特性:1)在平衡流体中,通过化而变化的流动。 水头(又称为静压)
pu,2g表示速度水头,
任意一点的等压面,必与该点所受的质量力26. 流线:是某一瞬时在流场中所作的一条曲线,表示总水头(又称为全z??
2g相互垂直。当流体处于绝对静止时,等压面在这条曲线上的各流体质点的速度方向都与压)。 ?
是水平面。2)当两种互不相溶的液体处于平衡状态时,分界面必定是等压面。
该曲线相切,因此流线是同一时刻,不同流体质点所组成的曲线。(1)同一时刻的不同流线,不能相交;(2)流线不能是折线,而是一条光滑的曲线;(3)流线簇的疏密反映了速度的大小。
27. 均匀流:是指流场中同一条流线各空间点上
的流速相同的流动,否则,则为非均匀流。 28. 非均匀流:非均匀流流场中相应点的流速大
小或方向同时沿程改变,即沿流程方向速度分布不均匀。
29. 渐变流是流速的大小和方向沿流线逐渐改变
的非均匀流。两个重要性质:1)渐变流过流断面近似为平面;2)渐变流过流断面上的压
40. 理想不可压缩的元流能量方程的几何意义说
明理想不可压缩流体在重力作用下作恒定流动时,沿同一流线(或微元流束)上各点的单位重量流体所具有的位置水头、压强水头和速度水头之和保持不变,即总水头是一常数。
? 内聚力?; 气体的分子热运动
? 分子间距? 内聚力?。
?: 液体的分子
Q??AudA(m3/s);质量流
3
?udA量:Qm?(m)。 udAAAQ??断面平均流速v??
A性方程A:恒定总流的连续
?A1?1u1dA1??A2?2u2dA2??1v1A1?
。对于不可压缩均质流体,由于
15. 对于不可压缩流体,密度
?是常数,
pz??C:不可压缩流体静压强
?g基本议程式的物理意义是:
pz是单位重量流体
对基准平面的位能,能
?g体具有的压力能,单位重量静止流体的压力
p
守恒定律在静止流体能量特性的表现。 16. 压强的计量基准:以完全真空(
是单位重量的流
241. 黏性流体恒定总流的能量方程(伯努利方程)
)p?0'
为基准起算的压强称为绝对压强,用p表示。以当地大气压强为基准来计量的压强称为相对压强,用p表示。绝对压强
?g
和位能z之和为一常数。这是能量
z1?
p1
'
?
?
?1v1
2g
?z2?
p2
?
?
2?2v2
2g
?hw1?
适用条件:1)流体是不可压缩的,流动为恒定流;2)质量力只有重力;3)过流断面为均匀流或渐变流断面;4)两过流断面间没有能量的输入或输出,否则应进行修正,修正如下:
p
'
总是
?2g?式中,H为单位重量流体流过水泵或风机所获得的
能量(取“正号”)或流进水轮机失去的能量(取“负
z1?
p1
?
?1v12
?H?z2?
p2
?
2
?2v2
?hw1?2。凡流线间夹角很小接近2g于平行线流动称为渐变流,反之称为急变流。
均匀流是流线为彼此平行的直线,应具有以
号”);5)若流动过程中有分流或汇流时,分别列出下特性: 断面1、2及断面1、3之间的伯努利方程 1、过流断面为平面,且过流断面的形状和尺
22对于:寸沿程不变; p1有1分v1流情p况22v2
2、同一流线上不同点的流速应相等,从而各z1???z2???hw1?2
2vg22vg2过流断面上的流速分布相同,断面平均流速,p3p13311
相等;z1???z3???hw1? 3222g2g;对p于有v汇流情p况:v理想不可压缩的恒定元流能量方程的物理意
333111
义h w1?3z1???z3???222g2g,沿同一流线(或微元流束)上各点的单位重p3p23v32v2
量流体所具有的位势能、压强势能和动能之z2???z3???hw2?3
2g2g和保持不变,即机械能是一常数,但位势能、。
??
?
??
?
??
??
??
??
??
在一定的流量下,设计出的渠道的过流断面
积达到最小,或者说在过流断面积一定时通过的流量最大。满足这些条件的断面,其工程量最小,称为水力最优断面。
临界底坡是一个假想底坡,与渠道实际底坡无关,仅与渠道流量Q、糙率n、断面形状尺寸有关
在棱柱形渠道中,断面形状尺寸、流量一定时,在渠中形成均匀流,若均匀流的正常水深恰好等于该流量的临界水深,则这个渠道的底坡就称为临界底坡。
跌水是明渠水流从缓流过渡到急流,水深从大于临界水深减至小于临界水深的过程中,水面急剧降落的局部的水力现象。
42. 注意的问题:1)弄清题意;2)选择合适的过流断面;3)选好基准面;4)求解流量时,一般要结合一维流动的连续性方程联立求解;5)能量方程的p1和p2应为同一度量单位,或同为绝对压强或同为相对压强;6)过流断面上的参数,如速度、压强和位置高度,应为同一点的参数。 静压强的两个重要特性: 1.静压强的方向与受压面垂直并指向受压面。 2.任一点静压强的大小和受压面方向无关,或者说作用于同一点上各方向的静压强大小相等。 等压面特性: 1.在平衡液体中,通过任意一点的等压面,必与该点所受质量力垂直。 2.当两种互不相溶的液体处于平衡状态时,分界面必定是等压面。 重力作用下静压强基本方程的物理意义: 在重力作用下的连续均质不可压所静止流体中,各点的单位重力流体的总势能保持不变。 几何意义:在重力作用下的连续均质不可压静止流体中,测压管水头线为水平线。 绝对压强:以完全真空为基准计量的压强。 相对压强:以当地大气压强为基准计量的压强。 描述液体运动的两种方法:拉格朗日法:(质点法)着眼于流体质点 欧拉法:(流场法)着眼于空间点 按各点运动要素(速度、压强)是否随时间而变化,可将流体运动分为恒定流和非恒定流。 恒定流:流动参数均不随时间变化的流动。特点:流场内的速度、压强、密度等参量只是坐标的函数,而与时间无关。当地加速度为零。 非恒定流:空间各点只要有一个流动参数量随时间变化的流动。 流线——是指某一瞬时,在流场中绘出的一条光滑的矢量曲线,其上所有各点的速度向量都与该曲线相切。 流线的性质: 1、流线不能相交,也不能转折,通过流场中的任一点只能画一条流线 2、流线的形状和疏密反映了某瞬时流场内液体的流速大小和方向,流线密的地方表示流速大,流线疏处表示流速小。 流体的流动按照它在同一流线上各质点的流速矢量是否沿流程变化,可分为均匀流和非均匀流。流场中所有流线是平行直线的流动,称为均匀流,反之称为非均匀流。 按流体的均匀程度的不同又将非均匀流动分
压强势能和动能三种能量之间可以相互转
换, 几何意义 沿同一流线(或微元流束)上各点的单位重量流体所具有的位置水头、压强水头和速度水头之和保持不变,即总水头是一常数 实际液体总流的总水头线必定是一条逐渐下降的线,而测压管水头线则可能是下降的线也可能是上升的线甚至可能是一条水平线。 应用能量方程式的条件 1)恒定流;(2)质量力只有重力;(3)不可压缩流体;(4)在所选取的两个过水断面上,水流应符合渐变流的条件,但所取的两个断面之间,水流可以不是渐变流;(5)在所取的两个过水断面之间,流量保持不变,其间没有流量加入或分出。若有分支,则应对第一支水流建立能量方程式,例如图示有支流的情况下,能量方程为: (6)流程中途没有能量H输入或输出。若有,则能量方程式应为: ? 孔口分类: 大孔口 d/H >0.1 小孔口 H/d ≤ 0.1 ? 流动分类:恒定和非恒定出流 ? 出流分类:自由出流和淹没出流 按照底坡进行分类 顺坡: i>0,明槽槽底沿程降低者称为正坡或顺坡。 平坡:i=0,明槽槽底高程沿程不变者称为平坡。逆坡:i<0,明槽槽底沿程增高者称为反坡或逆坡 明渠均匀流的水力特性: 1.均匀流过水断面的形状、尺寸沿流程不变。 2.过水断面上的流速分布和断面平均流速沿流程不变。 3.总水头线坡度、水面坡度、渠底坡度三者相等,即水流的总水头线、水面线和渠底线三条线平行。 明渠均匀流的形成条件 均匀流在水流方向上的重力分量与渠道边界的摩擦阻力相等,因此只能在正坡渠道才可能形成均匀流 1.水流必须是恒定流。 2.流量应沿程不变,即无支流的汇入或分出。 3.渠道必须是长而直的棱柱体顺坡明渠,粗糙系数沿程不变。 4.渠道中无闸、坝或跌水等建筑物的局部干扰
水跃是明渠水流从急流状态过渡到缓流状态时出现的水面突然跃起的局部水力现象。
43.
本文标题:工程流体力学-工程流体力学61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1