一 : 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

圆的周长ppt 圆的周长ppt

二 : 圆的周长ppt

址坊镇中心小学

圆的周长指什么？
围成圆的曲线的长就是圆的周长。

用什么办法测量出圆的周长呢？

可以用什么方法来测量圆 的周长呢？

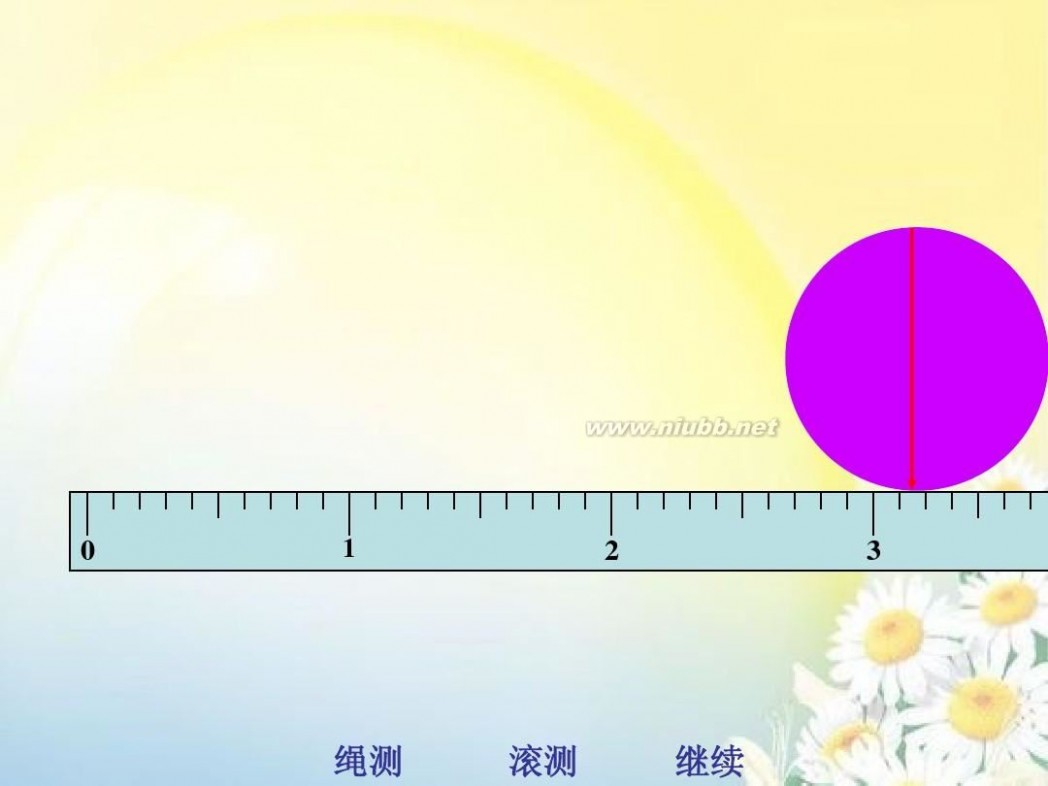
二、滚动法

0

1

2

3

绳测

滚测

继续

0

1

2

3

0

1

2

3

0

1

2

3

0

1

2

3

0

1

2

3

0

1

2

3

0

1

2

3

0

1

2

3

0

1

2

3

绳测

滚测

继续

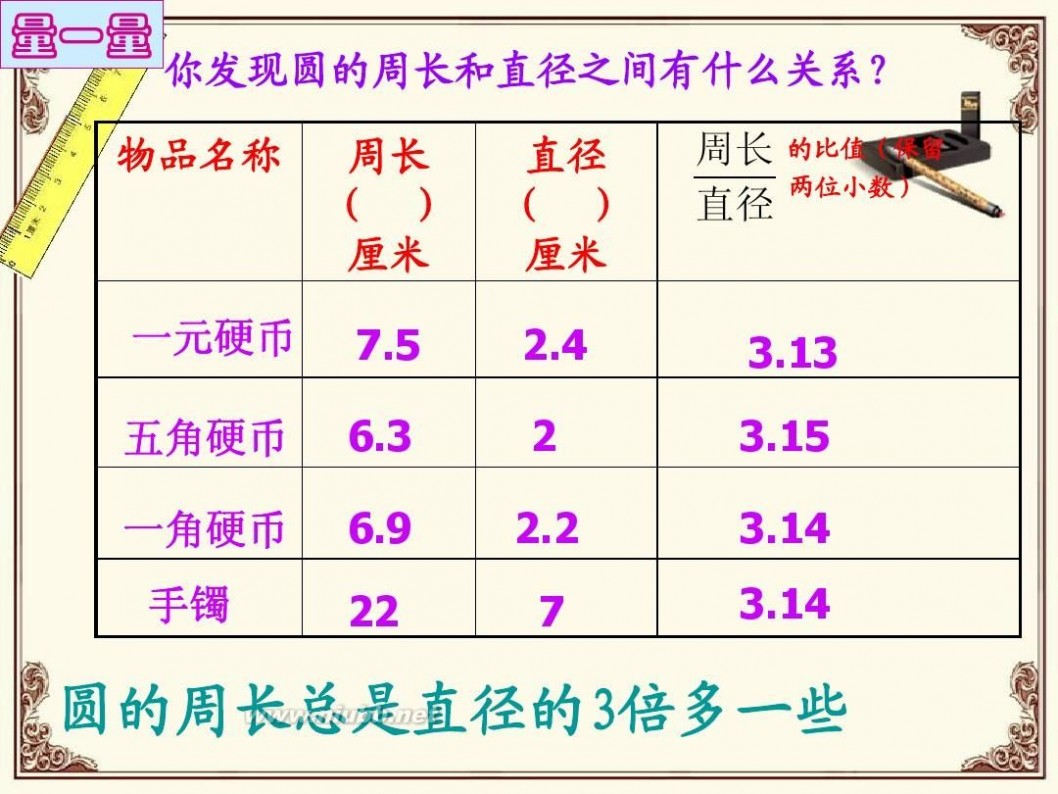
量一量

你发现圆的周长和直径之间有什么关系？ 周长 （ ） 厘米 7.5 6.3 6.9 直径 （ ） 厘米 2.4 2 2.2
周长 直径
的比值（保留 两位小数）

物品名称

一元硬币 五角硬币 一角硬币 手镯

3.13 3.15 3.14 3.14

22

7

圆的周长总是直径的3倍多一些

其实，圆的周长除以直径的商是一个固定 的数，我们把它叫做圆周率，用字母“π”表示。 “π”是一个无限不循环小数，它的值在 3.1415926至3.1415927之间，我们在计算的时 候通常取它的近似值3.14。

π＞3.14

约1500年前，中国有一位伟大的 数学家和天文学家祖冲之。他计算出 圆周率应在3.1415926 和3.1415927 之间，成为世界上第一个把圆周率的 值计算精确到7 位小数的人。他的这 项伟大成就比国外数学家得出这样精 确数值的时间，至少要早一千年。

π=3.1415926 535 897 932384626433832795028841971 693993751058209749445923078 164062862089986280348253421 170679821480865132823066470 938446095505822317253594081 284811174502841027019385211 055596446229489549303896442 881097566593344612847564823 378678316527120190914564856

圆的周长÷圆的直径=圆周率

C ÷ d = π 圆的周长 = 直径×圆周率
C = πd
C d= π C r= 2π

C = 2π r

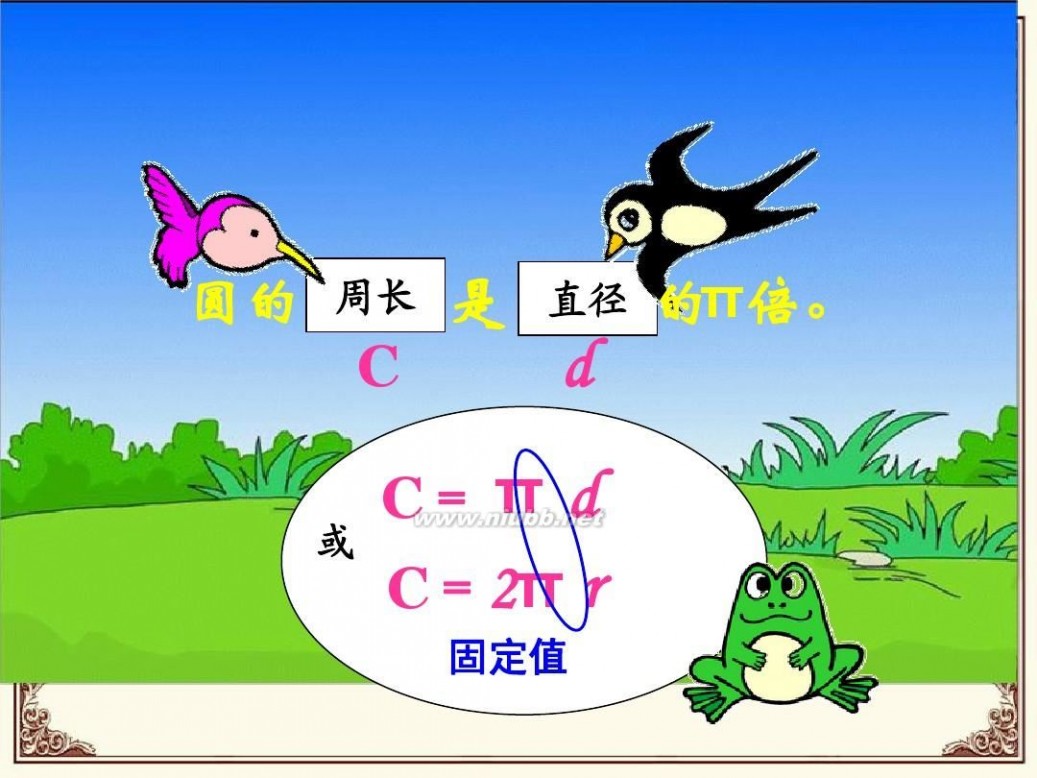
圆的

周长

是

直径

的π倍。

C
或

d

C＝ π

d C＝2π r
固定值

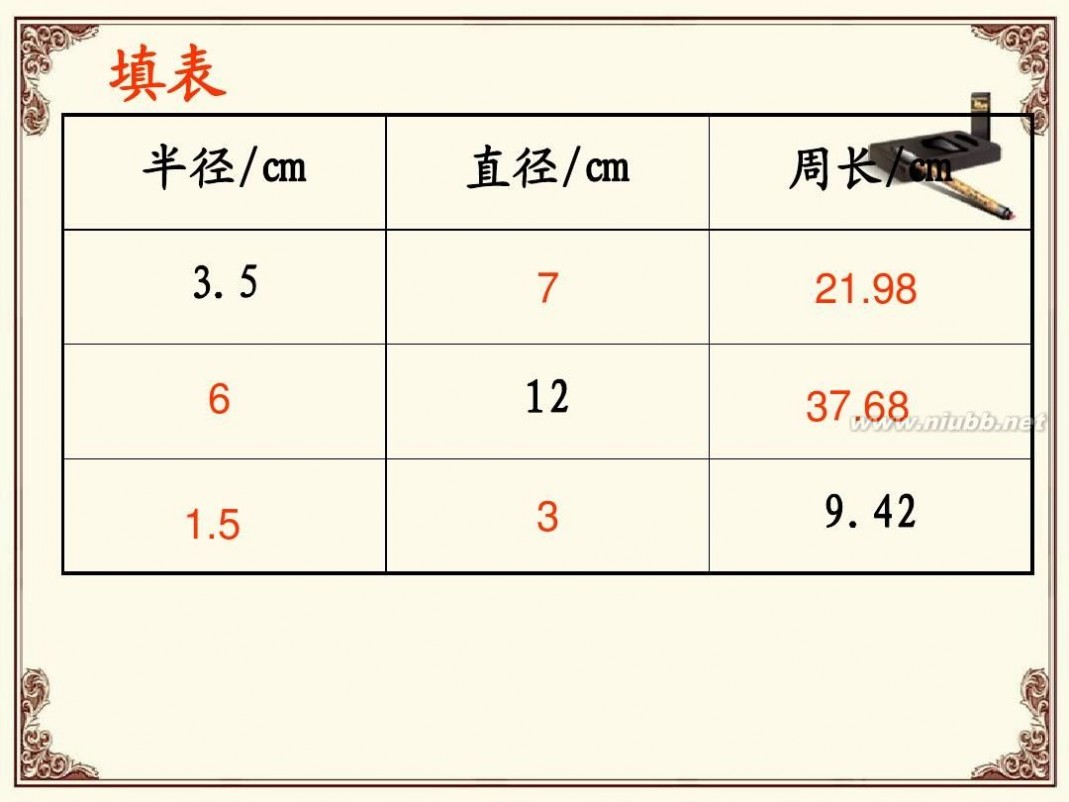
填表
半径/㎝ 3.5
6 1.5

直径/㎝
7

周长/㎝
21.98 37.68

12
3

9.42

（1）圆的直径越长圆周率越大。

数学诊所

（2）两个圆的周长相等半径就相等。 （3）圆的周长是它直径的π 倍。 （4）π ＝3.14。 （5）当一个圆的半径扩大2倍，它的周长 扩大4倍。

（6）大圆的圆周率比小圆的圆周率大。

明辨是非

1.任何圆的周长都是它的直径的π倍. ( √ ) 2.直径3厘米的圆比半径2厘米的圆的周长大. ( × ) 3.大圆的圆周率大于小圆的圆周率. (× )

练一练：求出下列各圆的周长
r=1.5米

C = πd
3.14×4 ＝12.56（厘米）

C = 2πr
3.14×(1.5×2)
＝3.14×3

＝9.42（米）

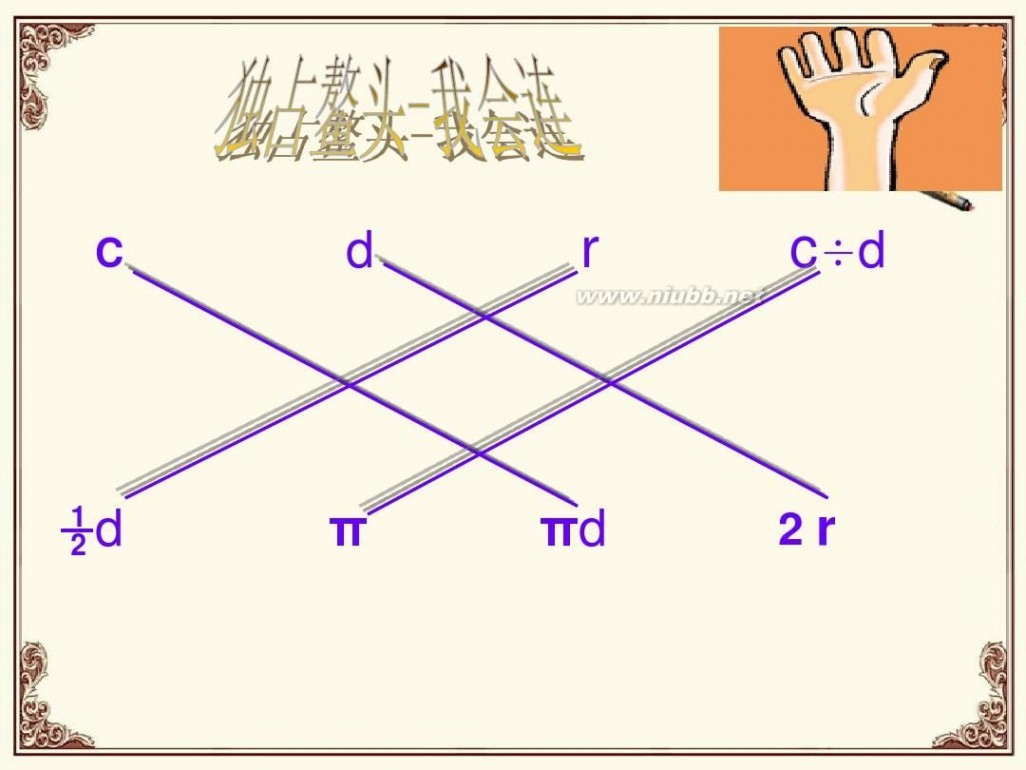
C

d

r

c ÷d

1 2

d

π

πd

2r

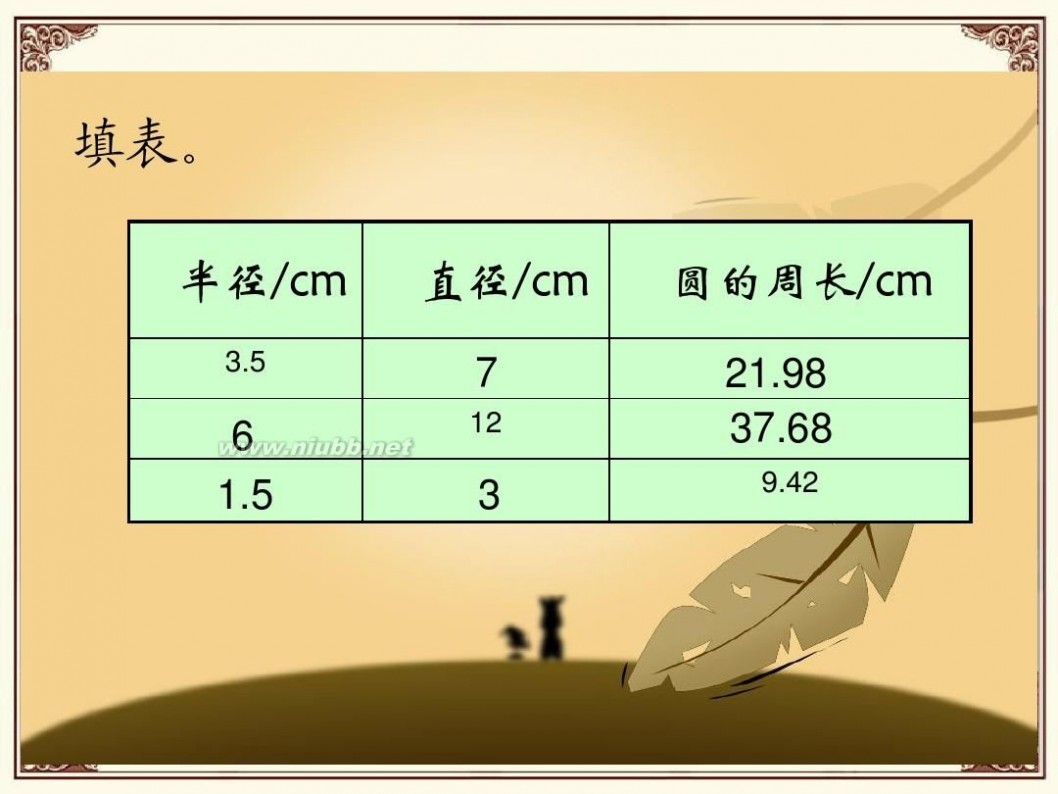
填表。
半径/cm
3.5

直径/cm
7
12

圆的周长/cm
21.98 37.68
9.42

6 1.5

3

摩天轮的半径是5米，坐着它转动一 周，大约在空中转过多少米？
3.14×(5×2) ＝31.4×10

＝31.4（米） 答：大约在空中转过31.4米。

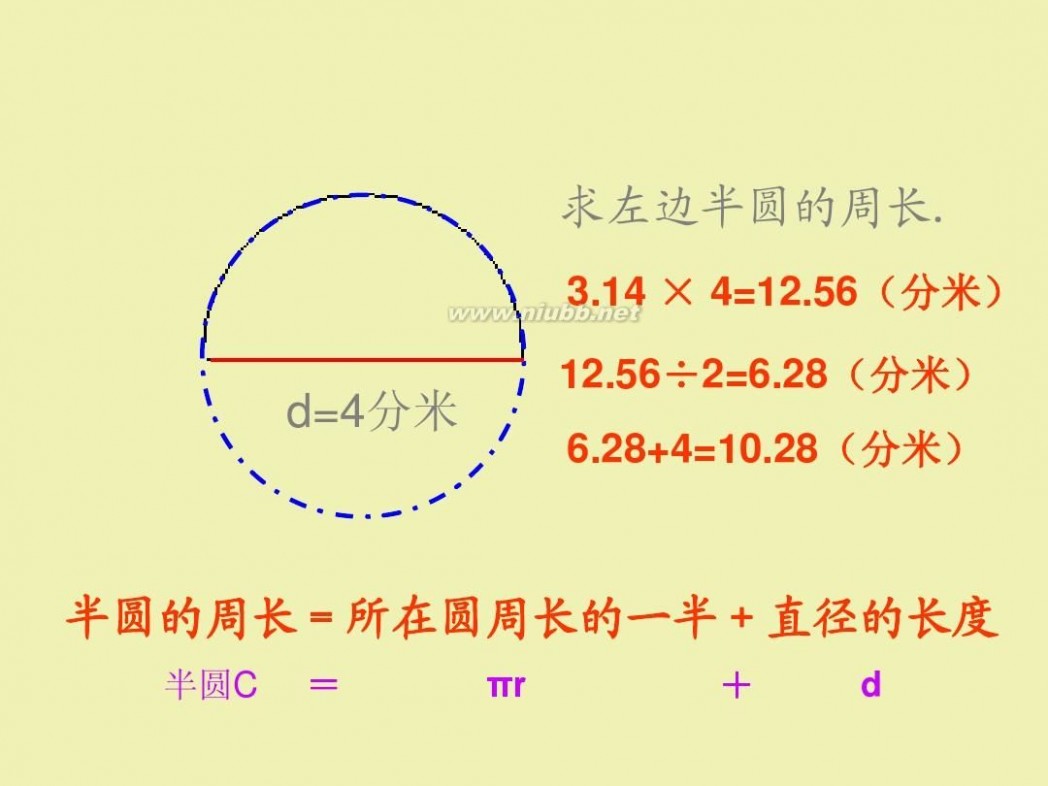
求左边半圆的周长.
3.14 × 4=12.56（分米）

d=4分米

12.56÷2=6.28（分米） 6.28+4=10.28（分米）

半圆的周长＝所在圆周长的一半＋直径的长度
半圆C ＝ πr ＋ d

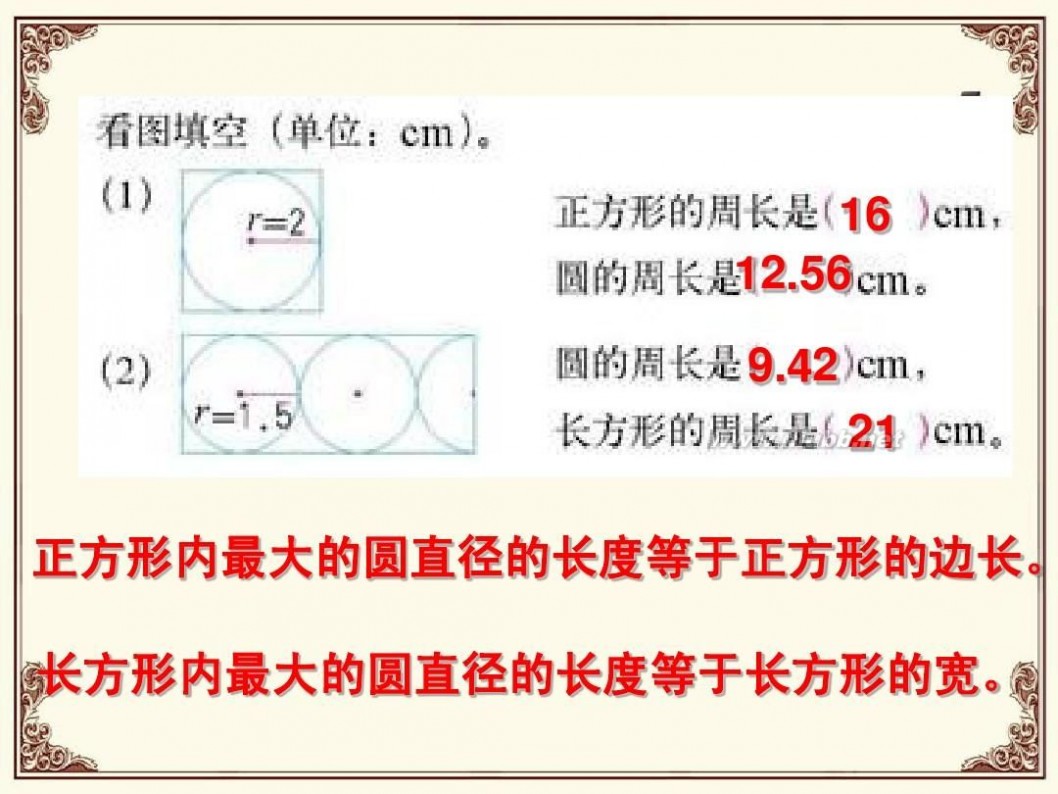
16 12.56 9

.42 21

正方形内最大的圆直径的长度等于正方形的边长。

长方形内最大的圆直径的长度等于长方形的宽。

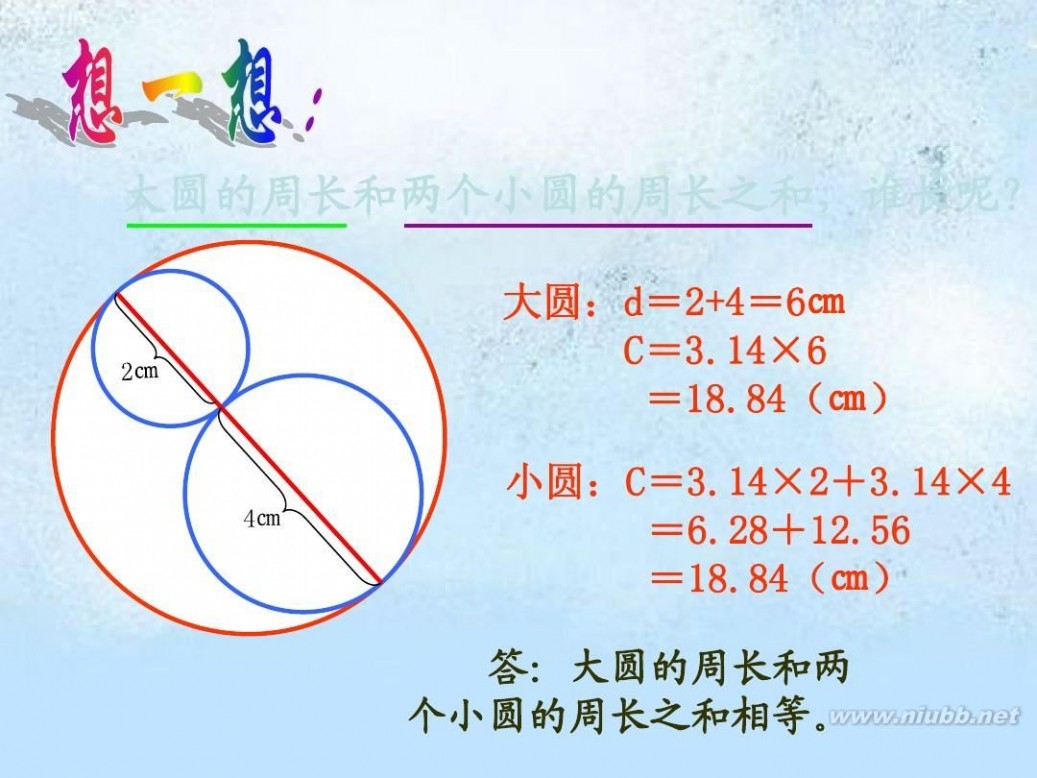
大圆的周长和两个小圆的周长之和，谁长呢？
大圆：d＝2+4＝6㎝ C＝3.14×6 ＝18.84（㎝）
4㎝

小圆：C＝3.14×2＋3.14×4 ＝6.28＋12.56 ＝18.84（㎝） 答：大圆的周长和两 个小圆的周长之和相等。

1．圆周率是（圆的周长 ）和（ 直径 ）的比值，
用字母（ π ）表示。它是一个（ 无限不循环 小数，计算周长时通常取近似值（ 3.14 ）。 ）

2．圆的周长的字母公式是（ C=πd ）或（ C=2πr ）。 公式说明：圆的周长是直径的（π ）倍，或是半径的 （ 2π ）倍。 3、自行车的车轮滚动一周，所行的路程是车轮的 （

周长

）。

4、把一块边长是10分米的正方形铁片，剪成一个最大的
圆形，这个圆的周长是（
d＝10

31.4分米

）。

C＝3.14×10＝31.4分米

5、已知圆的直径和正方形的边长相等，谁的周长更大一些？ C圆：3.14×4＝12.56（㎝）

4㎝

C正：4×4＝16（㎝） 答：正方形的周长更长。

半径

2周

1、一只大钟，分针长60厘米，2个小时后，分 针的尖端走了多少厘米？
C＝3.14×60×2 ＝188.4×2 ＝376.8（厘米） 答：分针的尖端走过了376.8厘米。
半径

2、一个挂钟，时针长40厘米，经过一昼夜，时 针的尖端走了多少厘米？
C＝3.14×40×2 ＝125.6×2 ＝251.2（厘米） 答：时针的尖端走过了251.2厘米。

2周

3、火车轮的外直径长0.9米，如果它分钟转400周， 那么这列火车每小时前进多少千米？
转一周：3.14×0.9=2.826（米） 转400周：2.826×400=1130.4（米） 一小时前进：1130.4×60=67824（米）

米

千米：67824米=67.824千米

答：这列火车每小时前进67.824千米。

4、一辆自行车的车轮半径是40厘米，车轮每分钟 转100圈，要通过2512米的桥，大约需要几分钟？
转一周：3.14×2×40=251.2（厘米） 转100周：251.2×100=25120（厘米） 厘米 米： 25120厘米=251.2米 2512÷251.2=10(分）

答：大约需要10分钟。

汽车轮胎的半径是0.3米，它滚动1000圈前 进多少米？ 下列解法哪个对？（ A、3.140.3×1000 B、1000÷（3.14×3） C、2×3.14×0.3×1000
C

）

–摩天轮的半径是10米，坐着它转动 一周是多少米？

C=2πr =2×10×3.14

6米
右图是一个一面靠墙，另 一面用篱笆围成的半圆形 养鸡场，这个半圆的直径 为6米，篱笆长多少米？

篱笆的长=周长的一半

C=6×3.14= 113.04
篱笆的长=56.52

（1）今天我学习了圆周长的知识。我知 道圆周率是（ 周长 ）和（ 直径）的比值， 它用字母（ π ）表示,它是我国古代数学 家（ 祖冲之 ）发现的。 （2）我还知道圆的周长总是 直径的（π ）倍。已知圆的直 径就可以用公式（ C＝π d ）求 周长；已知

圆的半径就可以用公 式（ C＝ 2π r ）求周长。

π≈3.14
直径d

我的收获

恭喜你！ 顺利过关！

你真棒！

三 : 圆周角ppt

圆周角

(1)

教者： 李生魁

一、复习回顾:
1.圆心角的定义?
答:顶点在圆心的角叫圆心角.
B C O

.

2.圆心角的度数和它所对的弧的度数的 关系?
答：相 等.

3.三角形的外角有什么性质？

练一练
1.如图，⊙O中，∠AOB=100o ，则AB弧的度

n O A 50o 度

100o 260o 数为______，AnB弧的度数为______。

B

2.如图（1），已知∠A=30o ∠B=20o ， ，则∠BCE=

如图（2）已知OA=OB=OC， ∠B=20o ∠C=30o ， ，则∠BOC= 100o 度 如图 （3）已知∠A=60o ∠B=40o ∠C=30o ， ， ，则∠BDC=

130o度

E
www.61k.com初中数学资源网

E

www.61k.com初中数学资源网

24.1圆周角 （第一课时）

www.61k.com初中数学资源网

学习目标:
1.理解圆周角的概念,掌握圆周 角定理. 2.准确地运用圆周角定理进行 简单的证明计算.

www.61k.com初中数学资源网

二、探究新知：
自学教材P84页内容，回答下列问题：
1.什么是圆周角？类比圆心角定义给圆周角下个 定义？ 2.圆周角有什么特征，用自己的话说一说？

探索1:
你能仿照圆心角的定义给圆周角下个定义吗?

圆周角定义:
顶点在圆上,并且两边 都和圆相交的角叫圆周角.
B

A

O C

.

特征： ①顶点在圆上.
②两边都与圆相交.

练习：
1.判别下列各图形中的角是不是圆周角，并说明理由。

不是
图１ 图２

不是
图３

是

不是
图４

不是
图５

类比圆心角探知圆周角
在同圆或等圆中,相等的弧所对的圆心角相等. 在同圆或等圆中, 相等的弧所对的圆周角有什么关系？ 为了解决这个问题,我们先探究一条弧所 对的圆周角和圆心角之间有的关系. 画一画，想一想，一条弧所对的圆心角有 多少个？圆周角有多少个

圆周角和圆心角的关系
如图,观察弧AC所对的圆周角∠ABC与

圆心角∠AOC,它们的大小有什么关系?
说说你的想法,并与同伴交流.

●

:注意圆心与圆周角的位置关系.

圆周角和圆心角的关系
1.首先考虑一种特殊情况： 当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周 角∠ABC与圆心角∠AOC的大小关系.

∵∠AOC是△ABO的外角， ∴∠AOC=∠B+∠A. ∵OA=OB， ∴∠A=∠B. ∴∠AOC=2∠B.
1 = 2∠AOC.

A

C
●

O

B

一条弧所对的圆 即 ∠ABC 周角等于它所对的圆 你能写出这个命题吗? 心角的一半.

圆周角和圆心角的关系
如果圆心不在圆周角的一边上,结果会怎样? 2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角 ∠ABC与圆心角∠AOC的大小关系会怎样? 想一想:能否转化为1的情况? 过点B作直径BD.由1可得: 1 1 ∠ABD = ∠AOD,∠CBD = ∠COD, 2 2
A D O C

●

1 ∴ ∠ABC = ∠AOC. 2

B

你能写出这个命题吗?

一条弧所对的圆 周角等于它所对的圆 心角的一半.

圆周角和圆心角的关系
如果圆心不在圆周角的一边上,结

果会怎样? 3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角 ∠ABC与圆心角∠AOC的大小关系会怎样? 想一想:能否也转化为1的情况?
A C B
●

过点B作直径BD.由1可得:
∠ABD =

O

1 一条弧所对的圆 ∴∠ABC = ∠AOC. 周角等于它所对的圆 2 你能写出这个命题吗? 心角的一半.

1 ∠AOD,∠CBD 2

1 = ∠COD, 2

圆周角定理
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是: 圆周角定理： 一条弧所对的圆周角等于它所对的圆心角的一半.
A O B

1 即 ∠ABC = ∠AOC. A 2
C

A

C

C
●

●

●

O

B

O

B

圆周角定理是承上启下的知识点,要予以重视.

做做看，收获知多少？
一、判断

1、顶点在圆上的角叫圆周角。（ × ）
2、圆周角的度数等于所对弧的度数的一半。（ √ ） 二、1、求圆中角x的度数
C O A D

120°

.
B

C A

70° x

O x

.
B

求图中角x的度数

x

x

x

35o
x 70°

80°
x
O
30° 120°

130°
O
x

O

120°

35°

60°

想一想

问题讨论

问题1：如图,在⊙ O 中,∠ABC,∠ADC,∠AEC 的大小有 什么关系?为什么?
D
B
●

O C

E

∠ABC = ∠ADC= ∠AEC ⌒ ⌒

A

连接BE，若AB=AC,则∠BEA与∠ADC 的大小又有什么关系？
若已知∠BEA与∠ADC，你又会得到什么 结论？为什么？www.61k.com初中数学资源网

想一想

问题讨论

问题2：如图1，BC是⊙O的直径，C是⊙O上任一 点，你能确定∠BAC的度数吗? ∠BAC =90o 问题3：如图2，圆周角∠BAC =90o ，弦BC经过 圆心O吗？为什么？
A B
A O

O
图1

C

B

●

C

图2

想一想

方法归纳

1、圆周角定理的推论1：

用于找相 等的角

同圆或等圆中，同弧或等弧所对的圆周角相等；
同圆或等圆中，相等的圆周角所对的弧也相等。

2、圆周角定理的推论2：
半圆（或直径）所对的圆周角是直角； 90°的圆周角所对的弦是直径。 用于判断某 条线是否过 圆心

用于找相 等的弧

用于判断某个 圆周角是否是 直角

例1:如图，AB是⊙O的直径，BD是⊙O的弦，延 长BD到C，使AC＝AB. BD与CD的大小有什么关系？ 为什么？
A O

C

D

B

解：BD＝CD. 理由是： 连接AD. ∵ AB是⊙O的直径， ∴ ∠ADB＝90°， 即 AD⊥BC. 又∵ AC＝AB， ∴ BD＝CD.

练一练
130° 2.如图，圆心角∠AOB=100°，则∠ACB=___。

O A
C
3、 如图，在直径为AB的半圆中，O为圆心，C、D为半 圆上的两点，∠COD=500，则∠CAD=_________ 25°

B

一、知识点： 圆周角 圆周角 定 理 推论：

顶点在圆上
两边都和圆相交 一条弧所对的圆周角，等于该弧所对的 圆心角的一半。 1、在同圆和等圆中，相等的弧所对的圆周 角相等；相等的圆周角所对的弧相等。 2、直径和半圆所对的圆周角是直角；90度 的圆周角的所对的弦是直径。

二、体现的数学思想：
由特殊到一般和分类讨论的思想。
www.1230

.org 初中数学资源网

作业：
1.p87第4题 ,P88第12题

⌒ ⌒ 2.(拓展）如图， ⊙O中，弦AB、CD相交于⊙O
外点P，且AC、BD度数分别为80°和20°，则如 何求∠APC的度数？

C
O

D
P B

A
www.61k.com初中数学资源网

结束寄语

下课了!

? 盛年不重来,一日难再晨

,及时宜自勉,岁月不待 人.

www.61k.com初中数学资源网

本文标题：圆的周长ppt-圆的周长ppt
本文地址： http://www.61k.com/1136634.html