一 : 在南京地铁二号线某路段铺轨工程中,先由甲工程队独做2天后,再由乙工程队独做3天刚好完成这项任务.已知乙工程队单独完成这项任务比甲工程队单独完成这项任务多用2天.请你根据以上信息,就“工作量”或“工作时间”,提出一个用分式方程解决的问题,并写出解答过程.
在南京地铁二号线某路段铺轨工程中,先由甲工程队独做2天后,再由乙工程队独做3天刚好完成这项任务.已知乙工程队单独完成这项任务比甲工程队单独完成这项任务多用2天.请你根据以上信息,就“工作量”或“工作时间”,提出一个用分式方程解决的问题,并写出解答过程.
本题答案不惟一,下列解法供参考.
解法一问题:甲工程队单独完成这项任务需要多少天?(2分)
设甲工程队单独完成这项任务需要x天,则乙工程队单独完成这项任务需要(x+2)天.(3分)
根据题意,得
| 2 |
| x |
| 3 |
| x+2 |
解得x1=4,x2=-1(舍去),
∴x=4(5分)
答:甲工程队单独完成这项任务需要4天.(6分)
解法二问题:乙工程队单独完成这项任务需要多少天?(2分)
设乙工程队单独完成这项任务需要x天,则乙工程队单独完成这项任务需要(x-2)天.(3分)
根据题意,得
| 2 |
| x−2 |
| 3 |
| x |
解得x1=6,x2=1(舍去),
∴x=6.(5分)
答:乙工程队单独完成这项任务需要6天.(6分)
二 : 一项工程,甲单独做需要12天,乙单独做需要9天.若甲先做若干天后?
一项工程,甲单独做需要12天,乙单独做需要9天.若甲先做若干天后乙接着做,共用10天完成,问甲做了几
一项,甲单独做需要12天,乙单独做需要9天.若甲先做若干天后乙接着做,共用10天完成,问甲做了几天?
设甲做了x天,
甲的日工作效率为1/12,乙的为1/9,
则x/12+(10-x)/9=1,
得x=4
三 : 甲、乙两个工程队完成某项工程,假设甲、乙两个工程队的工作效率是一定的,工程总量为单位1.甲队单独做了
甲、乙两个工程队完成某项工程,假设甲、乙两个工程队的工作效率是一定的,工程总量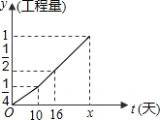 为单位1.甲队单独做了10天后,乙队加入合作完成剩下的全部工程,工程进度如图所示. 为单位1.甲队单独做了10天后,乙队加入合作完成剩下的全部工程,工程进度如图所示.(1)甲队单独完成这项工程,需______天. (2)求乙队单独完成这项工程所需的天数. (3)求出图中x的值. |
(1)由图可知,甲队单独干10天完成工程的
(2)甲乙两队合伙干了干了16-10=6天,完成工程的
两队合伙每天完成工程的
因为甲队甲队单独完成这项工程40天,故其每天完成工程的
故乙队单独完成这项工程所需的天数为1÷
答:乙队单独完成这项工程要60天. (3)
答:图中x的值是28. |
考点:
考点名称:函数的图像函数图象的概念:
对于一个函数,如果把自变量x和函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.
利用函数的图象解决实际问题,其关键是正确识别横轴和纵轴的意义,正确理解函数图象的性质,正确地识图、用图.
函数图象上的点的坐标与其解析式之间的关系:
①由图象的定义可知图象上任意一点P(x,y)中的x,y是解析式方程的一个解,反之,以解析式方程的任意一个解为坐标的点一定在函数图象上;
②通常判定点是否在函数图象上的方法是:将这个点的坐标代入函数解析式,如果满足函数解析式,这个点就在函数的图象上,如果不满足函数解析式,这个点就不在其函数的图象上,反之亦然;
③两个函数图像的交点就是饿两个函数解析式所组成的方程组的解。

四 : 在我县南城区某工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先
| 在我县南城区某工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成. (1)乙队单独完成这项工程需要多少天? (2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱? |
| 解:(1)设乙单独做需x天 根据题意列方程得: 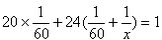 解之得:x=90, 经检验x=90是原方程的根,即乙单独做需90天; (2)甲单独做需60天,需工程款60×3.5=210 (万元) 设甲乙两队全程合作完成该工程需y天,y 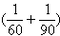 =1, =1,解得y=36,需工程款36×(3.5+2)=198(万元) ∴由甲乙两队全程合作完成该工程省钱。 |
考点:
考点名称:分式方程的应用列分式方程解应用题和列整式方程解应用题步骤基本相同,但必须注意,要检验求得的解是否为原方程的根,以及是否符合题意。
列分式方程解应用题的一般步骤是:
①找等量关系(审):理解题意,弄清具体情境中的已知量与未知量以及它们之间的基本关系;
②设:设未知数,用含x(或其他字母)表示某个未知数,由该未知数与其他数量的关系,写出表示相关量的式子;
③列:找出相等关系,列出分式方程;
④解:解这个分式方程;
⑤检验:双重检验,先检验是否为增根,再检验是否符合题意;
⑥答:写出答案。
例题
南宁到昆明西站的路程为828KM,一列普通列车和一列直达快车都从南宁开往昆明。直达快车的速度是普通快车速度的1.5倍,普通快车出发2H后,直达快车出发,结果比普通列车先到4H,求两次的速度.
设普通车速度是x千米每小时则直达车是1.5x
由题意得:
828/x-828/1.5x=6 ,
(828×1.5-828)/1.5x=6 ,
414/1.5=6x,
x=46, 1.5x=69
答:普通车速度是46千米每小时,直达车是69千米每小时。
无解的含义:
1.解为增根。
2.整式方程无解。(如:0x不等于0.)
用分式解应用题的常见题型:
(1)行程问题有路程、时间和速度三个量,其关系式是路程=速度×时间,一般式以时间为等量关系。
(2)工程问题有工作效率、工作时间和工作总量三个量,其关系式是工作总量=工作效率×工作时间。
(3)增长率问题,其等量关系式是原量×(1+增长率)=增长后的量,原量×(1+减少率)=减少后的量。
一元一次方程应用题型及技巧:
列方程解应用题的几种常见类型及解题技巧:
(1)和差倍分问题:
①倍数关系:通过关键词语“是几倍,增加几倍,增加到几倍,增加百分之几,增长率……”来体现。
②多少关系:通过关键词语“多、少、和、差、不足、剩余……”来体现。
③基本数量关系:增长量=原有量×增长率,现在量=原有量+增长量。
(2)行程问题:
基本数量关系:路程=速度×时间,时间=路程÷速度,速度=路程÷时间,
路程=速度×时间。
①相遇问题:快行距+慢行距=原距;
②追及问题:快行距-慢行距=原距;
③航行问题:
顺水(风)速度=静水(风)速度+水流(风)速度,
逆水(风)速度=静水(风)速度-水流(风)速度
例:甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
慢车先开出1小时,快车再开。两车相向而行。问快车开出多少小时后两车相遇?
两车同时开出,相背而行多少小时后两车相距600公里?
两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600公里?
两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车?
慢车开出1小时后两车同向而行,快车在慢车后面,快车开出后多少小时追上慢车? (此题关键是要理解清楚相向、相背、同向等的含义,弄清行驶过程。)
例:一艘船在两个码头之间航行,水流速度是3千米每小时,顺水航行需要2小时,逆水航行需要3小时,求两码头的之间的距离?
(3)劳力分配问题:抓住劳力调配后,从甲处人数与乙处人数之间的关系来考虑。 这类问题要搞清人数的变化。
例.某厂一车间有64人,二车间有56人。现因工作需要,要求第一车间人数是第二车间人数的一半。问需从第一车间调多少人到第二车间?
(4)工程问题:
三个基本量:工作量、工作时间、工作效率;
其基本关系为:工作量=工作效率×工作时间;相关关系:各部分工作量之和为1。
例:一件工程,甲独做需15天完成,乙独做需12天完成,现先由甲、乙合作3天后,甲有其他任务,剩下工程由乙单独完成,问乙还要几天才能完成全部工程?
(5)利润问题:
基本关系:
①商品利润=商品售价-商品进价;
②商品利润率=商品利润/商品进价×100%;
③商品销售额=商品销售价×商品销售量;
④商品的销售利润=(销售价-成本价)×销售量。
⑤商品售价=商品标价×折扣率例.
例:一家商店将某种服装按进价提高40%后标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的进价是多少?
(6)数字问题:一般可设个位数字为a,十位数字为b,百位数字为c,十位数可表示为10b+a, 百位数可表示为100c+10b+a,然后抓住数字间或新数、原数之间的关系找等量关系列方程。
数字问题中一些表示:两个连续整数之间的关系,较大的比较小的大1;
偶数用2n表示,连续的偶数用2n+2或2n—2表示;奇数用2n+1或2n—1表示。
例:有一个三位数,个位数字为百位数字的2倍,十位数字比百位数字大1,若将此数个位与百位顺序对调(个位变百位)所得的新数比原数的2倍少49,求原数。
(7)盈亏问题:“盈”表示分配中的多余情况;“亏”表示不足或缺少部分。
(8)储蓄问题:
其数量关系是:
利息=本金×利率×存期;:(注意:利息税)。
本息=本金+利息,利息税=利息×利息税率。
注意利率有日利率、月利率和年利率,年利率=月利率×12=日利率×365。
(9)溶液配制问题:
其基本数量关系是:溶液质量=溶质质量+溶剂质量;
溶质质量=溶液中所含溶质的质量分数。
这类问题常根据配制前后的溶质质量或溶剂质量找等量关系,分析时可采用列表的方法来帮助理解题意。
(10)比例分配问题:
这类问题的一般思路为:设其中一份为x,利用已知的比,写出相应的代数式。
常用等量关系:各部分之和=总量。
还有劳力调配问题、配套问题、年龄问题、比赛积分问题、增长率问题等都会有涉及。
五 : 一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:(
| 一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问: (1)乙队单独做需要多少天能完成任务? (2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x、y都是整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天? |
| (1)设乙队单独做需要x天完成任务. 根据题意得
解得 x=100. 经检验x=100是原方程的解. 答:乙队单独做需要100天完成任务. (2)根据题意得
整理得 y=100-
∵y<70,∴100-
解得 x>12. 又∵x<15且为整数, ∴x=13或14. 当x=13时,y不是整数,所以x=13不符合题意,舍去. 当x=14时,y=100-35=65. 答:甲队实际做了14天,乙队实际做了65天. |
考点:
考点名称:分式方程的应用列分式方程解应用题和列整式方程解应用题步骤基本相同,但必须注意,要检验求得的解是否为原方程的根,以及是否符合题意。
列分式方程解应用题的一般步骤是:
①找等量关系(审):理解题意,弄清具体情境中的已知量与未知量以及它们之间的基本关系;
②设:设未知数,用含x(或其他字母)表示某个未知数,由该未知数与其他数量的关系,写出表示相关量的式子;
③列:找出相等关系,列出分式方程;
④解:解这个分式方程;
⑤检验:双重检验,先检验是否为增根,再检验是否符合题意;
⑥答:写出答案。
例题
南宁到昆明西站的路程为828KM,一列普通列车和一列直达快车都从南宁开往昆明。直达快车的速度是普通快车速度的1.5倍,普通快车出发2H后,直达快车出发,结果比普通列车先到4H,求两次的速度.
设普通车速度是x千米每小时则直达车是1.5x
由题意得:
828/x-828/1.5x=6 ,
(828×1.5-828)/1.5x=6 ,
414/1.5=6x,
x=46, 1.5x=69
答:普通车速度是46千米每小时,直达车是69千米每小时。
无解的含义:
1.解为增根。
2.整式方程无解。(如:0x不等于0.)
用分式解应用题的常见题型:
(1)行程问题有路程、时间和速度三个量,其关系式是路程=速度×时间,一般式以时间为等量关系。
(2)工程问题有工作效率、工作时间和工作总量三个量,其关系式是工作总量=工作效率×工作时间。
(3)增长率问题,其等量关系式是原量×(1+增长率)=增长后的量,原量×(1+减少率)=减少后的量。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1