一 : 数列{an}是公比为的等比数列,且1
数列{an}是公比为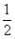 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n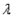 ·bn+1( ·bn+1(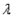 为常数,且 为常数,且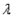 ≠1). ≠1).(I)求数列{an}的通项公式及 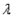 的值; 的值;(Ⅱ)比较 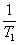 + +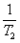 + +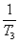 + + + +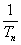 与了 与了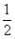 Sn的大小. Sn的大小. |
(1)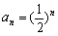 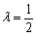 (2) (2)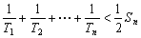 |
试题分析:解:(Ⅰ)由题意 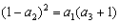 ,即 ,即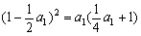 解得  ,∴ ,∴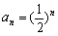 2分 2分又  ,即 ,即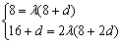 4分 4分解得 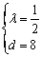 或 或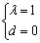 (舍)∴ (舍)∴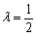 6分 6分(Ⅱ)由(Ⅰ)知 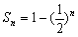 7分 7分∴ 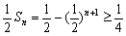 ① 9分 ① 9分又 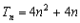 , ,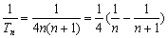 11分 11分∴ 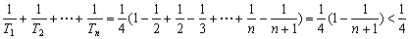 ② 12分 ② 12分由①②可知 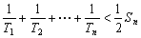 13分 13分点评:解决的关键是根据已知数列的特点,结合裂项法来求和,属于中档题。 |
考点:
考点名称:等差数列的定义及性质等差数列的定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做公差,用符号语言表示为an+1-an=d。
等差数列的性质:
(1)若公差d>0,则为递增等差数列;若公差d<0,则为递减等差数列;若公差d=0,则为常数列;
(2)有穷等差数列中,与首末两端“等距离”的两项和相等,并且等于首末两项之和;
(3)m,n∈N*,则am=an+(m-n)d;
(4)若s,t,p,q∈N*,且s+t=p+q,则as+at=ap+aq,其中as,at,ap,aq是数列中的项,特别地,当s+t=2p时,有as+at=2ap;
(5)若数列{an},{bn}均是等差数列,则数列{man+kbn}仍为等差数列,其中m,k均为常数。
(6)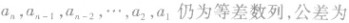
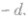
(7)从第二项开始起,每一项是与它相邻两项的等差中项,也是与它等距离的前后两项的等差中项,即

(8)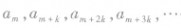 仍为等差数列,公差为
仍为等差数列,公差为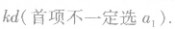
对等差数列定义的理解:
①如果一个数列不是从第2项起,而是从第3项或某一项起,每一项与它前一项的差是同一个常数,那么此数列不是等差数列,但可以说从第2项或某项开始是等差数列.
②求公差d时,因为d是这个数列的后一项与前一项的差,故有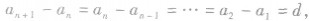 还有
还有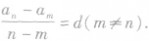
③公差d∈R,当d=0时,数列为常数列(也是等差数列);当d>0时,数列为递增数列;当d<0时,数列为递减数列;
④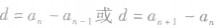 是证明或判断一个数列是否为等差数列的依据;
是证明或判断一个数列是否为等差数列的依据;
⑤证明一个数列是等差数列,只需证明an+1-an是一个与n无关的常数即可。
等差数列求解与证明的基本方法:
(1)学会运用函数与方程思想解题;
(2)抓住首项与公差是解决等差数列问题的关键;
(3)等差数列的通项公式、前n项和公式涉及五个量:a1,d,n,an,Sn,知道其中任意三个就可以列方程组求出另外两个(俗称“知三求二’).
等比数列的定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做公比,公比通常用字母q表示(q≠0)。
等比数列的性质:
在等比数列{an}中,有
(1)若m+n=p+q,m,n,p,q∈N*,则aman=apaq;当m+n=2p时,aman=ap2;
(2)若m,n∈N*,则am=anqm-n;
(3)若公比为q,则{ }是以
}是以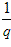 为公比的等比数列;
为公比的等比数列;
(4)下标成等差数列的项构成等比数列;
(5)
1)若a1>0,q>1,则{an}为递增数列;
2)a1<0,q>1, 则{an}为递减数列;
3)a1>0,0<q<1,则{an}为递减数列;
4)a1<0, 0<q<1, 则{an}为递增数列;
5)q<0,则{an}为摆动数列;若q=1,则{an}为常数列。

如何证明一个数列是等比数列:
证明一个数列是等比数列,只需证明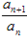 是一个与n无关的常数即可(或an2=an-1an+1)。
是一个与n无关的常数即可(或an2=an-1an+1)。
二 : 一个等比数列an中,a1+a4=133,a2+a3=70,求这个?
一个等比数列an中,a1+a4=133,a2+a3=70,求这个?
一个等比数列an中,a1+a4=133,a2+a3=70,求这个数列的通项公式,设等比数列an的公比为q(q≠0)则:a2=a1*q,a3=a1*q^2,a4=a1*q^3所以:a1+a1*q^3=133 ===>a1*(1+q^3)=133a1*q+a1*q^2=70 ========>a1*q*(1+q)=70………………(1)两式相除得到:(1+q^3)/[q*(1+q)]=1.9===>(1+q)(1-q+q^2)/[q*(1+q)]=1.9===>1-q+q^2=1.9q===>q^2-2.9q+1=0===>10q^2-29q+10=0===>(5q-2)(2q-5)=0===>q1=2/5,或者q2=5/2当q=2/5时代入(1)得到:a1*(2/5)*(7/5)=70所以,a1=125则,an=a1*q^(n-1)=125*(2/5)^(n-1)当q=5/2时代入(1)得到:a1*(5/2)*(7/2)=70所以,a1=8则,an=a1*q^(n-1)=8*(5/2)^(n-1)
三 : 在等比数列{an}中.a1>0.n∈N*.且a3-a2=8.
试题详情61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1