一 : 若关于x的不等式x

若关于x的不等式 x-m＜0 7-2x≤1 的整数解共有4个，则m的取值范围是______．

题型：填空题难度：中档来源：椒江区二模

x-m＜0① 7-2x≤1② ， 由①得：x＜m， 由②得：x≥3， ∴不等式组的解集是3≤x＜m， ∵关于x的不等式 x-m＜0 7-2x≤1 的整数解共有4个， ∴6＜m≤7， 故答案为：6＜m≤7．

考点：

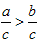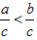考点名称：不等式的性质不等式的性质：
1、不等式的基本性质:
不等式性质1：不等式的两边同时加上（或减去）同一个数（或式子），不等号的方向不变。即如果a>b，那么a±c>b±c。
不等式性质2：不等式的两边同时乘（或除以）同一个正数，不等号的方向不变。即如果a>b，c>0，那么ac>bc（或）。

不等式性质3：不等式的两边同时乘（或除以）同一个负数，不等号的方向改变。即如果a>b，c<0，那么ac<bc（或）。
2、不等式的互逆性：若a>b，则b<a。
3、不等式的传递性：若a>b，b>c，则a>c。

不等式的性质：
①如果x>y，那么y<x；如果y<x，那么x>y；（对称性）
②如果x>y，y>z；那么x>z；（传递性）
③如果x>y，而z为任意实数或整式，那么x+z>y+z；（加法原则，或叫同向不等式可加性）
④ 如果x>y，z>0，那么xz>yz；如果x>y，z<0，那么xz<yz；（乘法原则）
⑤如果x>y，z>0，那么x÷z>y÷z；如果x>y，z<0，那么x÷z<y÷z；
⑥如果x>y，m>n，那么x+m>y+n；(充分不必要条件)
⑦如果x>y>0，m>n>0，那么xm>yn；
⑧如果x>y>0，那么x的n次幂>y的n次幂（n为正数)，x的n次幂<y的n次幂（n为负数）

或者说，不等式的基本性质有：
①对称性；
②传递性：
③加法单调性：即同向不等式可加性：
④乘法单调性：
⑤同向正值不等式可乘性：
⑥正值不等式可乘方：
⑦正值不等式可开方：
⑧倒数法则。

不等式的基本性质和等式的基本性质的异同：
①相同点：无论是等式还是不等式，都可以在它的两边加（或减）同一个数或同一个整式；
②不同点：对于等式来说，在等式的两边乘（或除以）同一个正数（或同一个负数），等式仍然成立，但是对于不等式来说，却不大一样，在不等式的两边乘（或除以）同一个正数，不等号的方向不变，而在不等式的两边乘（或除以）同一个负数，不等号要改变方向。

原理：
①不等式F（x）< G（x）与不等式 G（x）>F（x）同解。
②如果不等式F（x） < G（x）的定义域被解析式H（ x ）的定义域所包含，那么不等式 F（x）<G（x）与不等式F（x）+H（x）<G（x）+H（x）同解。
③如果不等式F（x）<G（x） 的定义域被解析式H（x）的定义域所包含，并且H（x）>0，那么不等式F(x)<G（x）与不等式H（x）F（x）<H（ x ）G（x） 同解；如果H（x）<0，那么不等式F（x）<G（x）与不等式H (x)F（x）>H（x）G（x）同解。
④不等式F（x）G（x）>0与不等式同解；不等式F（x）G（x）<0与不等式同解。

考点名称：一元一次不等式的解法

一元一次不等式的解集：
一个有未知数的不等式的所有解，组成这个不等式的解集。例如﹕
不等式x-5≤-1的解集为x≤4；
不等式x﹥0的解集是所有正实数。

求不等式解集的过程叫做解不等式。
将不等式化为ax>b的形式
(1)若a>0，则解集为x>b/a
(2)若a<0，则解集为x<b/a

一元一次不等式的特殊解：
不等式的解集一般是一个取值范围，但有时需要求未知数的某些特殊解，如求正数解、整数解、最大整数解等，解答这类问题关键是明确解的特征。

不等式的解与解集：
不等式成立的未知数的值叫做不等式的解。如x=1是x+2>1的解
①不等式的解是指某一范围内的某个数，用它来代替不等式中的未知数，不等式成立。
②要判断某个未知数的值是不是不等式的解，可直接将该值代入等式的左、右两边，看不等式是否成立，若成立，则是；否则不是。
③一般地，一个不等式的解不止一个，往往有无数个，如所有大于3的数都是x>3的解，但也存在特殊情况，如|x|≦0，就只有一个解，为x=0

不等式的解集和不等式的解是两个不同的概念。
①不等式的解集一般是一个取值范围，在这个范围内的每一个数值都是不等式的一个解，不等式一般有无数个解。
②不等式的解集包含两方面的意思：
解集中的任何一个数值，都能使不等式成立；解集外的任何一个数值，都不能使不等式成立。（即不等式不成立）
③不等式的解集可以在数轴上直观的表示出来，如不等式x-1<2的解集是x<3,可以用数轴上表示3的点左边部分来表示，在数轴上表示3的点的位置上画空心圆圈，表示不包括这一点。

一元一次不等式的解法：
解一元一次不等式与解一元一次方程的方法步骤类似，只是在利用不等式基本性质3对不等式进行变形时，要改变不等式的符号。
有两种解题思路：
（1）可以利用不等式的基本性质，设法将未知数保留在不等式的一边，其他项在另一边；
（2）采用解一元一次方程的解题步骤：去分母、去括号、移项、合并同类项、系数化为1等步骤。

解一元一次不等式的一般顺序：
（1）去分母 （运用不等式性质2、3） 　　
（2）去括号 　　
（3）移项 （运用不等式性质1） 　　
（4）合并同类项。 　　
（5）将未知数的系数化为1 （运用不等式性质2、3） 　　
（6）有些时候需要在数轴上表示不等式的解集

不等式解集的表示方法：
（1） 用不等式表示：一般的，一个含未知数的不等式有无数个解，其解集是一个范围，这个范围可用最简单的不等式表达出来。
例如：x-1≤2的解集是x≤3。 　　
（2） 用数轴表示：不等式的解集可以在数轴上直观地表示出来，形象地说明不等式有无限多个解。
用数轴表示不等式的解集要注意两点：一是定边界线；二是定方向。

考点名称：一元一次不等式组的解法

一元一次不等式组解集：
一元一次不等式组中各个不等式的解集的公共部分叫做这个不等式组的解集。
注：当任何数x都不能使各个不等式同时成立，我们就说这个一元一次不等式组无解或其解集为空集。
例如：
不等式x-5≤-1的解集为x≤4；
不等式x﹥0的解集是所有非零实数。
解法：求不等式组的解集的过程，叫做解不等式组。

求几个一元一次不等式的解集的公共部分，通常是利用数轴来确定的，公共部分是指数轴上被两条不等式解集的区域都覆盖的部分；
一般由两个一元一次不等式组成的不等式组由四种基本类型确定，它们的解集、数轴表示如下表：（设a<b）

一元一次不等式组的解答步骤：
（1）分别求出不等式组中各个不等式的解集；
（2）将这些不等式的解集在同一个数轴上表示出来，找出它们的的公共部分；
（3）根据找出的公共部分写出不等式组的解集，若没有公共部分，说明不等式组无解。

解法诀窍：
同大取大 ；
例如：
X>-1
X>2
不等式组的解集是X>2

同小取小；
例如：
X<-4
X<-6
不等式组的解集是X<-6

大小小大中间找；
例如，
x<2,x>1,不等式组的解集是1<x<2

大大小小不用找
例如，
x<2,x>3，不等式组无解

一元一次不等式组的整数解：
一元一次不等式组的整数解是指在不等式组中各个不等式的解集中满足整数条件的解的公共部分。
求一元一次不等式组的整数解的一般步骤：先求出不等式组的解集，再从解集中找出所有整数解，其中要注意整数解的取值范围不要搞错。
例如



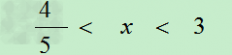
所以原不等式的整数解为1，2。

二 : 若关于Ｘ的不等式组ax>-1,x+a>0 有解，则实a?

不等式组

若关于Ｘ的不等式组ax>-1,x+a>0 有解，则实a的取值范围是

---

如果a>=0, 那么x+a>0--->x>-a. 与ax>-1显然有解，比如x=1即为一解。

如果a<0, ax>-1--->x<-1/a, 但x+a>0--->x>-a. 因此必须有-a<-1/a,a^2<1, -1

因此当a满足a>-1时，方程组有解。

三 : 若关于x的不等式组x-3≥a,b-x≥-2的解集为x=2b+a+?

若关于x的不等式组x-3≥a,b-x≥-2的解集为x=2b+a+1

若关于x的不等式组x-3≥a,b-x≥-2的解集为x=2b+a+1,求:使得关于x的不等式组x-k≥a,x+k<b无解的K的取值范围.

---

由x-3≥a，得x≥a+3,

由b-x≥-2，得x≤b+2

又因为不等式组x-3≥a,b-x≥-2的解集为x=2b+a+1

所以：a+3=b+2=2b+a+1

解得a=0,b=1

所以不等式组x-k≥a,x+k

x-k≥0,x+k<1

解得1-k>x≥k

若要不等式组无解，

只需满足1-k≤k

解得k≥1/2

四 : 要使满足关于x的不等式2x^2-9x+a<0(解集非空）的?

取值范围

要使满足关于x的不等式2x^2-9x+a<0(解集非空）的每一个x的值，至少满足不等式x^2-4x+3<0,和x^2-6x+8<0中的一个，求实数a的取值范围.

---

要使满足关于x的不等式2x²-9x+a＜0(解集非空）的每一个x的值，至少满足不等式x²-4x+3＜0和x²-6x+8＜0中的一个，求实数a的取值范围

A={x|x²-4x+3＜0}=(1,3)

B={x|x²-6x+8＜0|=(2,4)

根据题意，C={x|2x²-9x+a＜0}是A∪B=(1,4)的子集

即：f(x)=2x²-9x+a=0的两根在(1,4)内

--->(1) Δ=9²-8a≥0---->a≤81/8

(2) f(1)=a-7＞0--->a＞7

(3) f(4)=a-4＞0--->a＞4

--->4＜a≤81/8

五 : 关于x的不等式x^2-(k+1)x+2-k＜0的解集为空集，则k?

关于x的不等式x^2-(k+1)x+2-k＜0的解集为空集，则k的取值范围是多少

关于x的不等式x^2-(k+1)x+2-k＜0的解集为空集，则k的取值范围是多少不等式(5x-4)/(x+4)≤2的解集区间是

---

不等式x^2-(k+1)x+2-k＜0的解集为空集

则判别式<=0,所以（k+1)^2-4*(2-k)≤0,k^2+6k-7≤0

(k+7)(k-1)≤0,解得-7≤k≤1

(5x-4)/(x+4)≤2,(5x-4)/(x+4)-2≤0,得（x-4)/(x+4)≤0,

所以-4≤x≤4

本文标题：若关于x的不等式-若关于x的不等式x
本文地址： http://www.61k.com/1111508.html