一 : 找规律 写数字 怎样的规律得怎样的数字
二 : 法语数字规律表
1 5 9un, une cinq neuf2 6 10 14 18 22 26 30 70deux six dix quatorze dix-huit vingt-deux vingt-six trente soixante-dix3 7 11 15 19 23 27 40 80trois sept onze quinze dix-neuf vingt-trois vingt-sept quarante4 quatre 8 huit 12 douze 16 seize 20 vingt 24 vingt-quatre 28 vingt-huit 50 cinquante13 treize 17 dix-sept 21 vingt et un(une)25 vingt-cinq 29 vingt-neuf 60 soixante 100 cent注意:quatre-vingts 90 quatre-vingt-dix1000 mille10000 dix mille1. 法语的数字中,除了 onze(11),soixante et onze(71),quatre-vingt-onze (91)没有性的变化,其它带“1”的数词在遇到阴性名词前均要配合。[www.61k.com)如果是阴性,要用 “une”,例如: trente et une cartes 31 张卡片quatre-vingt-une filles 81 个女孩 mille et une Nuits 一千零一夜,天方夜谭 2. 一般来说,quatre-vingts 后面要加上“s”(因为是 4 个 20,是复数)。但如果后面还 有其它数词,就不用加“s”,例如,quatre-vingt-trois (83) 3. cent 的配合方法原则上和 vingt(20)相同,在复数时要加“s”,但如果后面还有其它 数字,就不用加“s”。例如: cinq cents (500) neuf cent cinquante (950) cent un (une)(101),deux cents(200) neuf cent quatre-vingt-dix-neuf (999) 4. mille 是不变数词,在任何情况下都不用加“s”。 5. 法语中的 1100 到 1900 可以说“mille cents,mille neuf cents”,也可以说“onze cents”(11 个 100,1100)“dix neuf cents”(19 个 100,1900)
水蜜桃别墅 法语数字规律表
注:法国的电话号码为八位数,念法每两位一组,例如 12 34 56 78 读法是 douze, trente-quatre, cinquante-six,soixante-dix-huit。(www.61k.com]
数字什么的很苦恼吧?没有关系,掌握规则就好!中国的用法是四位四位一念,而法语数词是坚持的“三三制”原则——三个一组,慢慢数。怎么样,不难吧?
1. 000 000 000 三个一组,按百位数的读法来读,后面加相应的量就行了。
|milliard(十亿)|million(百万)|mille( 千)
ex. 65 891 377 000 soixante-cinq milliards huit cent qutre-vinght-onze millions trois cent soixante-dix-sept mille
2. *quatre- vingts(80)一般情况下,词尾应加s,但如果后面还有其它数字就不加s #quatre- vingts filles
#quatre- vingt trois filles
*cent (百) 的用法同上
cent personnes
six cents personnes
six cent trois personnes
*mille(千) 任何时候词尾都不加入s
61阅读提醒您本文地址:
三 : 数字推理规律总结
<2> 表格形式数字推理
行间运算规律:行间运算规律主要是每行两个数字简单运算得到第三个数.主要有下面三种形式:
每行前两个数运算得到第三个数.
每行后两个数运算得到第一个数.
每行第一个数和第三个数运算得到中间数字.
<3> 三角形形式数字推理
三角形数字推理的规律通常是寻找三角形的数字与中心数字之间的联系
一、圆圈形数字推理
1、考虑对角数字和周围数字
【例】

A.27 B. 21 C. 16 D. 11
【答案】C
【解题关键点】考虑对角数字和周围数字
5×8+(13+7)=2,3×12+(3+15)=2,15×4+(19+11)=2
2、考虑四周数字得到中间数字的方式
解题思想
1.思考角度:一般由四周向中间位置的数靠拢。[www.61k.com)
2.运算关系:一般各数之间为“加减乘除”关系,其中加法、减法、乘法是最常见的运算方法。
3.组合关系:一般采用上下、左右、对角三种组合关系。
4.如果中间位置的数是质数,那么一般是通过加法或减法向中间位置靠拢;如果中间位置的数是合数(特别的一些质数也可分解为其与1的乘积),则可以首先将中间位置拆分成
两个(或三个)因数的乘积,再将已知数向因数靠拢,也可以通过加减法向中间位置数靠拢。
5.如果中间位置数值较大,而其他数值较小,则考虑运算中含有乘法关系。
6.作减法和除法时,注意减数和被减数、除数和被除数的位置关系。 要点提示
奇偶数之间有如下的运算法则:
偶数±偶数=偶数,奇数±奇数=偶数,奇数±偶数=奇数
偶数×偶数=偶数,奇数×奇数=奇数,奇数×偶数=偶数
根据以上法则可以得到以下规律:
(1)几个偶数之间做四则运算无法得到一个奇数。
(2)偶数个奇数之间的无法通过加法得到一个奇数,偶数个奇数之间无法
数字推理 数字推理规律总结
通过乘法得到一个偶数。[www.61k.com)
【例】

A.3 B. 5 C. 7 D. 9
【答案】C
【解题关键点】考虑四周数字得到中间数字的方式
3×4-5-6=1,3×5-5-8=2,4×5-6-11=3
2012浙江公务员行测特色题型突破:图形形式数字推理
我们知道,无论是何种形式的图形形式的数字推理,其考查的规律都是关于数字之间的运算关系,所以解题时分析也就围绕运算关系展开。而在图形形式数字推理中,由于数字较少,分析方法也就相对简单。中公教育专家归纳了以下几个考虑的角度,结合例题予以说明。由于解题环境各不相同,普遍之中难免例外,还望考生自己多加琢磨,此处仅抛砖引玉。
一、分析四周数字之和与中心数字的大小关系
如果四周数字之和小于中心数字,则四周数字的运算过程很有可能涉及乘法运算,否则,就应该优先考虑减法或除法运算。这种分析虽然过程简单,但有利于确定大致的方向。
例题:

A.6 B.12 C.13 D.7
中公解析:此题答案为B。从前两个图形来看,四周数字之和远大于中心数字,这时需要将四周数字分组,优先考虑它们之间的减法或除法运算。第一个图形中有24、12、6,第二个图形中有8、8、16,这些数都为除法创造了条件。若在第一个图形中,24÷12;则在第二个图形中,8÷16,得到的是小数,由此否定这条路。即应该是24÷6,得到4,和中心数字6相差2,2可由12和10得到,此题便得到了解决。
第一个图形中,24÷6+12-10=6;第二个图形中,8÷8+16-9=8;第三个图形中,32÷8+20-12=(12)。
二、分析图形中最大的数
数字推理 数字推理规律总结
在数字推理中,几个数字运算得到另一个数字,通常都是几个较小的数运算得到一个较大的数。(www.61k.com)如果几个较小的数字运算得到一个远大于它们的数,则一定要通过乘法等使数字增大的运算。因此我们可以以图形中最大的数字作为突破口,寻找运算关系。
例题1:

A.11 B.16 C.18 D.19
中公解析:此题答案为D。图形中最大的数字是第三个图形中68,它由6、2、4三个数字运算得到,68远大于这三个数字的和,考虑乘法运算,三个数字的积是6×2×4=48,仍然小于68,由此确定应该考虑使数字变化更快的乘方运算。68附近的多次方是64,考虑到这些,这个题目就不难解决了。

三、分析图形中的质数
质数由于只能被1和它本身整除,它们在运算过程中,更多的时候,要涉及加法或减法运算,这是我们分析图形中质数的原因。
例题1:
数字推理 数字推理规律总结
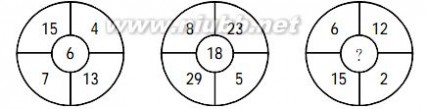
A.27 B.12 C.30 D.24
中公解析:此题答案为B。[www.61k.com]前两个图形中的质数较多,在第一个图形中7、13等质数都大于中心数字6;在第二个图形中23、29都大于中心数字18;显然四周数字运算时,涉及到这些质数的倍数的可能性不大,这些质数更大可能是要进行加法、减法运算。
按照这种思路,不难确定此题规律。第一个图形中,(15-13)×(7-4)=6;第二个图形中,(8-5)×(29-23)=18;第三个图形中,(6-2)×(15-12)=(12)。
例题2:
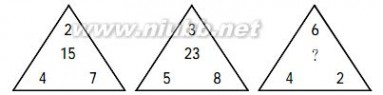
A.26 B.29 C.31 D.37
中公解析:此题答案为A。第一个图形中有质数7,中心数字是15,它不是7的倍数,则7在运算过程中极有可能涉及加法或减法;第二个图形中,中心数字23是质数,它由3、5、8运算得到,运算过程中也极有可能涉及加法或减法。
61阅读提醒您本文地址:
此题三个数运算得到第四个数,这些简单的运算关系相信大家通过数列形式数字推理的学习,已经很熟悉了。第一个图形中,2×4+7=15;第二个图形中,3×5+8=23;第三个图形中,6×4+2=(26)。
目前,图形数字推理常见的题型有三种:㈠圆圈型数字推理:1、有心圆圈型;2、无心圆圈型;㈡九宫格数字推理:3×3网格形式;㈢其他几何型数字推理:1、三角形;2、环形;3、正方形;4、长方形
一、圆圈型数字推理
1、有心圆圈型:周边数字通过运算得到中间圈内的数字。
2、无心圆圈型:周边数字之间满足一个基本运算等式。
解题一般规律
1、基本规律是通过加减乘除,较少情况用到“倍数”和“乘方”。
2、运算方向一般为上下、左右、交叉(交叉最常见)。
(一) 有心圆圈型
数字推理 数字推理规律总结
1、奇数法则:(1)如果每个圆圈中都是偶数个奇数,那么解题一般从“加减”入手。[www.61k.com](2)如果有一个圆圈中有奇数个奇数,那么这道题一般无法通过“加减”完成,应该优先考虑“乘法”和“除法”。
2、非奇数解法:(1)先加减,后相乘。如果前面两个中心数字容易分解,先对其分解,然后在周边数字中构造因数。(2)先乘除,后加减。如果两个中心数字有一个较大且不易分解,应先从周边数字出发,选取两个先相乘,然后进行修正。
(二)无心圆圈型
1、运算目标:有心圆圈型一般以中心数字为运算目标,而无心圆圈型从形式上看没有一个确定的目标,那么一般的运算目标我们定位为,圆圈中的两个数字的加减乘除=两外两个数字的加减乘除。
2、当无心圆圈型涉及到乘法,优先考虑较小数字相乘。
3、把一个两位数字拆分成个位数和十位数,分别放在圆圈的两个位置得考法,大家一定要注意。
二、九宫格数字推理
(一)等差等比型(最简单,越来越少考):数字沿行方向与列方向呈等比或等差规律。
(二)分组计算型:九宫格中按照行和列分组计算,得到的结果呈简单规律。
(三)线性递推型(较常见):一般模式为“第一列的a倍加上第二列的b倍等于第三列”,但目标数列可能是第一列,也可能是第三列。
三、其他几何型数字推理
(一)三角形:中心数字为运算的目标数字。
(二)正方形(略)
61阅读提醒您本文地址:
四 : 找规律,填数字。1. Whatnumberismissingfromthefinal (最后的) b
61阅读/ www.61k.net
| 找规律,填数字。 |
| 1. Whatnumberismissingfromthefinal (最后的) box? 2. Whichnumbercomesnext? 12 21 30 39 48 ___________ |
| 1. 2 2. 57 |
考点:
考点名称:基数词基数词:
即表示数目多少的数词。
A、1-12的基数词表示方法。
1 one 2 two 3 three 4 four 5 five 6 six 7 seven 8 eight 9 nine10 ten 11 eleven12 twelve
B、13-19基数词的表示方法,都以teen结尾。
13 thirteen 14 fourteen 15 fifteen 16 sixteen 17 seventeen 18 eighteen 19 nineteen
C、大于20小于100的基数词的表示方法。
a. 整数词的表示方法,都以ty结尾。
20 twenty 30 thirty 40 forty 50 fifty 60 sixty 70 seventy 80 eighty 90 ninety
b. 其他的两位数的表示方法:先写比表示从20-90的英文单词,然后是连字符“-”,最后写从1-9的英文单词。
如:21 twenty-one 55 fifty-five 92 ninety-two
D、整百的基数词的表示方法,用1-9加hundred表示。表示几百,在几十几与百位间加上and。
100 a (one) hundred 200 two hundred 900 nine hundred
101 a hundredand one 320 three hundred and twenty 648six hundred and forty-eight
注:hundred 前面有具体数字时,后面不能加“s”;这个词表示大概数字时词尾要加“s”。如:hundreds of (数以百计)。
E、千位数以上 从数字的右端向左端数起,每三位数加一个逗号“,”。从右开始,第一个“,”前的数字后添加 thousand,第二个“,”前面的数字后添加 million,第三个“,”前的数字后添加 billion。然后一节一节分别表示,两个逗号之间最大的数为百位数形式。
2,648 two thousand six hundred and forty-eight
16,250,064 sixteen million two hundred and fifty thousand sixty-four
5,237,166,234 five billion,two hundred and thirty-seven million,one hundred and sixty-six thousand,two hundred and thirty-four
F、基数词在表示确切的数字时,不能使用百、千、百万、十亿的复数形式;但是,当基数词表示不确切数字,如成百、成千上万,三三两两时,基数词则以复数形式出现。
There are hundreds of people in the hall. 大厅里有数以百计的人。
Thousands and thousands of people come to visit the Museum of Qin Terra-Cotta Warriors and Horses every day. 每天有成千上万的人来参观秦兵马俑博物馆。
基数词的复数形式:
有时两个复数形式的基数词连用可写为:
hundreds of thousands of , tens of hundreds of 等等。
They went to the theatre in twos and threes.他们三三两两地来到了剧院。
表示人的不确切岁数或年代,用几十的复数形式表示。
He became a professor in his thirties.他三十多岁时成为了教授。
She died of lung cancer in forties.她四十来岁时死于肺癌。
It was in the 1960s.那是在二十世纪六十年代。
基数表示法:
一、小数表示法
1. 小数用基数词来表示,以小数点为界,小数点左首的数字为一个单位,表示整数,数字合起来读;
小数点右首的数字为一个单位,表示小数,数字分开来读;
小数点读作 point,o读作 zero或o〔ou〕,整数部分为零时,可以省略不读。
0.4 zero point four或point four 零点四
10.23 ten point two three 十点二三
25.67 twenty-five point six seven 二十五点六七
l.03 one point o three 一点零三
2. 当数字值大于1时,小数后面的名词用复数,数字值小于1时,小数后面的名词用单数。
1.03 meters 一点零三米
0.49 ton 零点四九吨
l.5 tons 一点五吨
二、时刻表示法
1. 表示几点钟用基数词加可以省略的o/’clock
5:00 读作 five o/’clock 或 five
2. 表示几点过几分,在分钟后加past,再加小时
five past seven 七点过五分
half past six 六点半
a quarter past eight 八点过一刻
seven past eight 八点过七分
3. 表示几点差几分,在分钟后面加to,再加小时
ten to eight 差十分八点(七点五十分)
a quarter to twelve 差一刻十二点(十一点四十五分)
twenty to six 差二十分六点(五点四十分)
在日常生活中,常用下列简单方法表示时间。
以小时、分种为单位分别读出数字。
6:31 读作 six thirty-one
10:26 读作 ten twenty-six
14:03 读作 fourteen o three
16:15 读作 sixteen fifteen
18:30 读作 eighteen thirty
23:55 读作 twenty-three fifty-five
注:时刻表上的时间大多采用24小时表示法,这样就不需要用a.m.表示上午,p.m.表示下午了。
三、年月表示法
1. 世纪可以用定冠词加序数词加世纪century表示,也可以用定冠词加百位进数加/’s表示
the sixth(6th)century 公元六世纪
the eighteenth(18th)century 公元十八世纪
the 1900/’s 二十世纪
the 1600/’s 十七世纪
这里,用百位数整数表示的世纪比这一百位阿拉伯数字本身多一个世纪。
2. 年代用定冠词及基数词表示的世纪加十位整数的复数形式构成
in the 1930/’s(in the thirties of the twentieth century或 in the nineteen thirties)
在二十世纪三十年代
in the 1860/’s(in the sixties of the 19th century或 in the eighteen sixties)
在十九世纪六十年代
In the 1870/’s when Marx was already in his fifties,he found it important to study the situation in Russia,so he began to learn Russian.
在十九世纪七十年代当马克思已经五十多岁时,他发现研究俄国的形势很重要,便开始学习俄语。
3. 表示某年代的早期、中期和晚期,可以在定冠词后,年代前添加 early,mid-,late
in the early 1920/’s 在二十世纪二十年代早期
in the mid-1950/’s 在二十世纪五十年代中期
4. 年月日表示法
A.年份用基数词表示,一般写为阿拉伯数字,读时可以以hundred为单位,也可以以世纪、年代为单位分别来读。
1949 读作 nineteen hundred and forty-nine 或 nineteen forty-nine
1800 读作 eighteen hundred
253 读作 two hundred and fifty-three或two fifty-three
1902 读作 nineteen hundred and two或 nineteen o two
表示在哪一年,一般在年数前加介词in,使用year时,year放在数词之前。
in the year two fifty-three B.C. 在公元前253年
但是,通常采用in加表示年份的阿拉伯数字。
B. 月份,在哪个月用介词in加第一个字母大写的月份词表示。
例如:in May在五月; in July在七月。
为了简便起见,月份与日期连用时,月份常用缩写形式表示。
缩写形式除May,June,July外,其它的月份都由其前三个字母表示,但September除外。
January——Jan.一月
February——Feb.二月
March——Mar. 三月
April——Apr.四月
August——Aug.八月
September——Sept.九月
October——Oct.十月
November——Nov.十一月
December——Dec.十二月
注:这里缩写形式后面加点不能省略,因为它是表示缩写形式的符号。
C.日期用定冠词the加序数词表示。在哪一天要添加介词on。
National Day is on Oct. 1.
国庆节是十月一日。(读作 October first)
此句也可以表示为 National Day is on the 1st of October.
May 5 五月五日(读作May fifth)
也可以表示为the fifth(5th)of May
Mar. 1(st) 三月一日(读作March first或 the first of March)
5. 表示不具体、不确切的时间,如世纪、年代、年份、月份时,用介词in表示;
表示具体确切的某一天用介词on表示通常情况下morning,afternoon,evening等词前用介词in。
但是,当这些词前后有一修饰限定的词作为定语,把它们限定为某一天早晨、下午或晚上时,介词in应改为on。
这里的修饰限定词可以是介词短语、名词、形容词、定语从句等。
On a cold morning,the old man died lonely in his house.
在一个寒冷的早晨,这个老人孤独地死在自己的房子里。
I don/’t want to be disturbed on nights when I have to study.
我不愿意在我必须学习的晚上被打扰。
The accident happened on the afternoon of July 7.
这次事故发生在7月7日下午。
We are to have a small test on Monday morning.
星期一早晨我们将进行一次小测验。
四、加减乘除表示法
1. “加”用plus,and或add表示;“等于”用is,make,equal等词表示。
2+3=? 可表示为: How much is two plus three?
2+3=5
Two plus three is five.
Two and three is equal to five.
Two and three make five.
Two added to three equals five.
If we add two to/and three, we get five.
二加三等于五
2. “减”用 minus或 take from表示
10-6=? How much is ten minus six?
10-6=4
Ten minus six is four.
Take six from ten and the remainder is four.
Six (taken) from ten is four.
十减去六等于四
3. “乘”用time(动词)或multiply表示
3×4=? How much is three times four?
3×4=12
Three times four is/are twelve.
Multiply three by four,we get twelve.
Three multiplied by four makes twelve.
三乘以四等于十二
4. “除”用divide的过去分词形式表示
16÷4=? How much is sixteen divided by four?
16÷4=4
Sixteen divided by four is four.
Sixteen divided by four equals/gives/makes four.
十六除以四等于四。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1