一 : 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

扩展：精算师金融数学真题 / 精算师 金融数学 / 精算师考试金融数学

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

扩展：精算师金融数学真题 / 精算师 金融数学 / 精算师考试金融数学

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

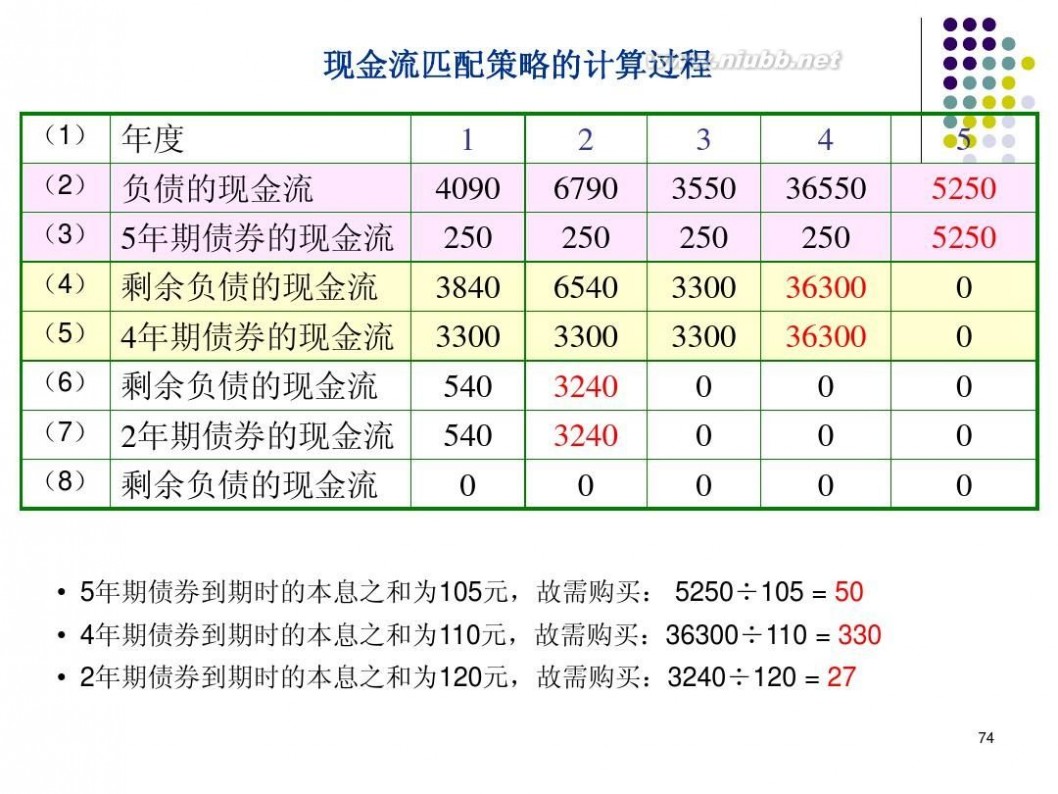
精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

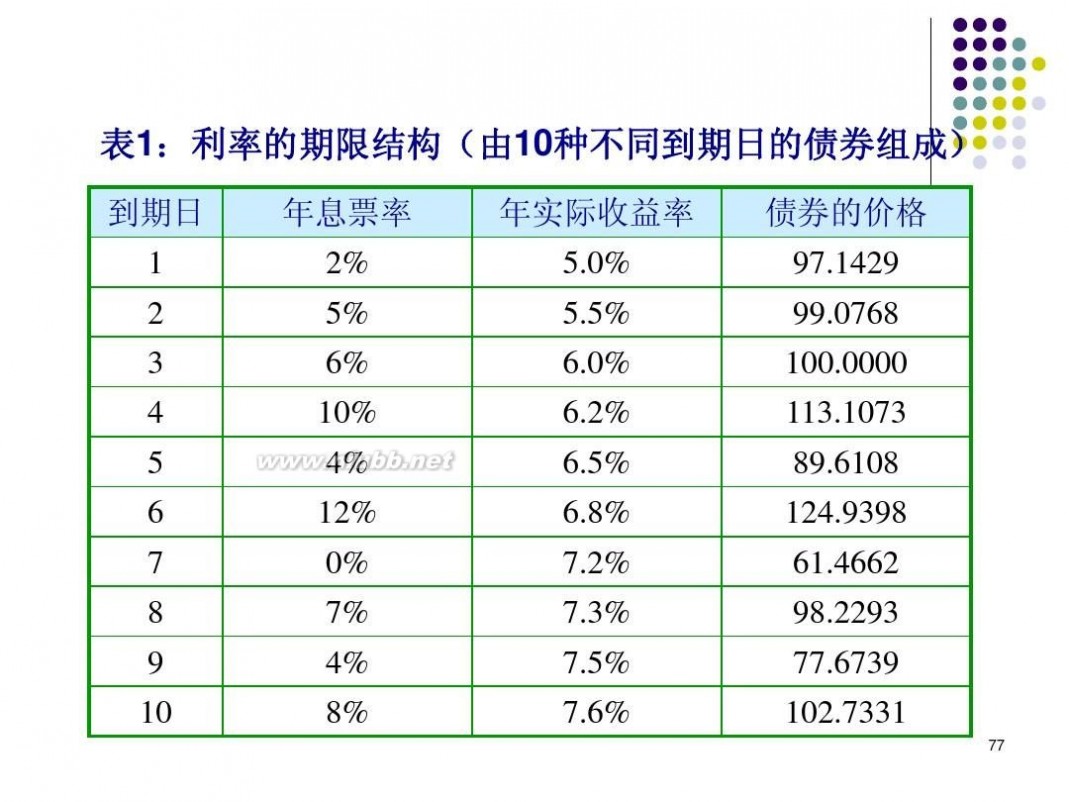
精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

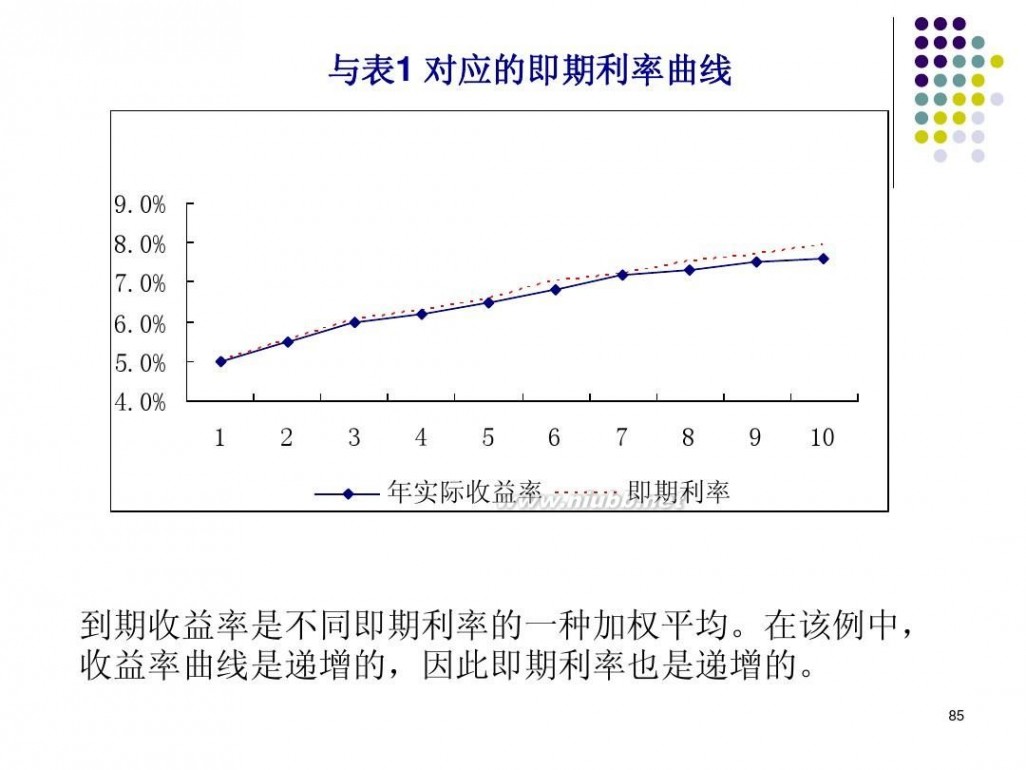
精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

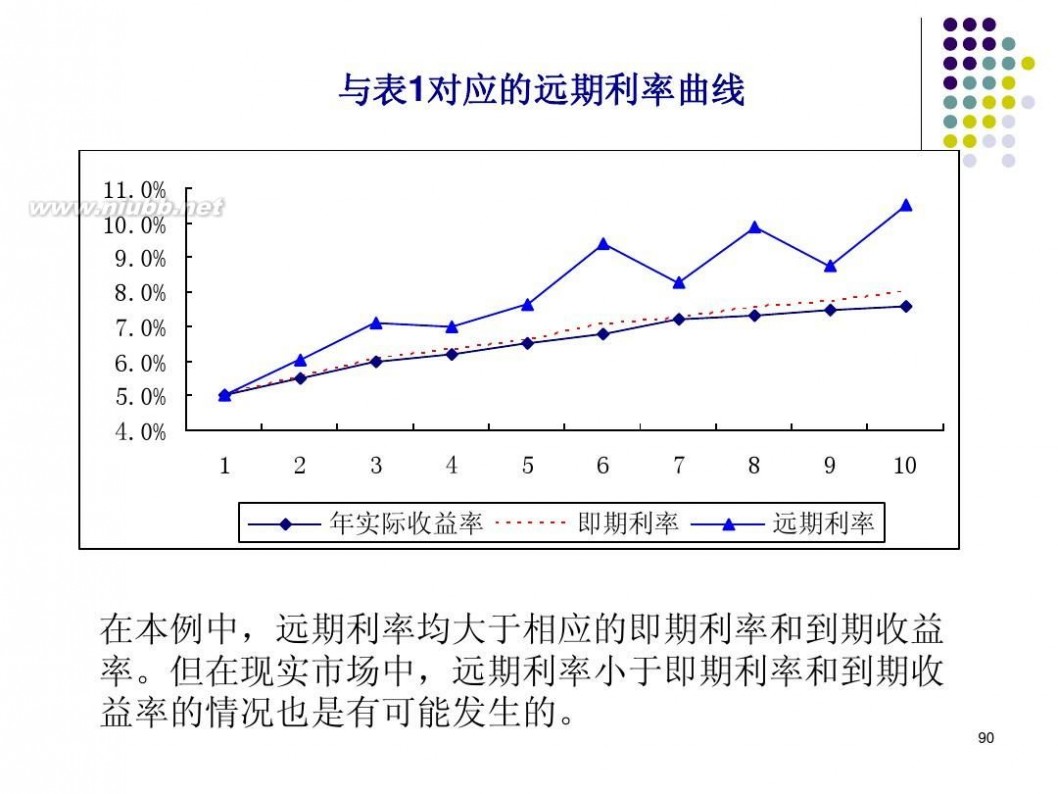
扩展：精算师金融数学真题 / 精算师 金融数学 / 精算师考试金融数学

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

精算师培训 《金融数学》精算师培训

（www.61k.com]

扩展：精算师金融数学真题 / 精算师 金融数学 / 精算师考试金融数学

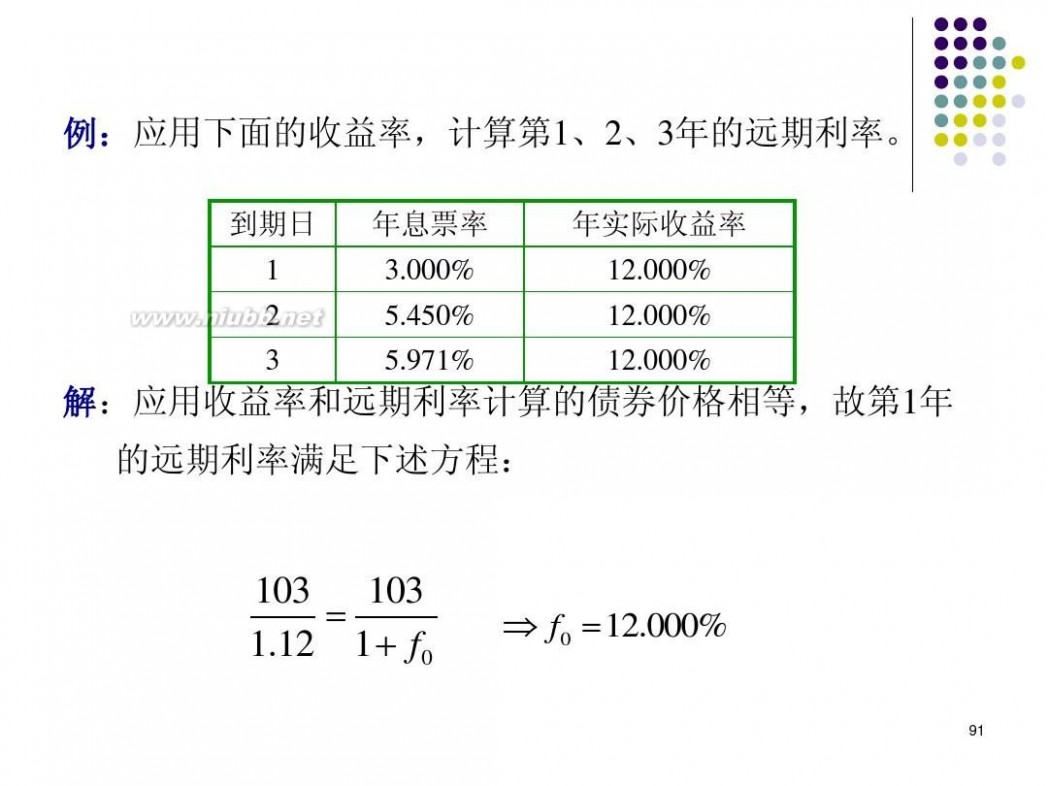
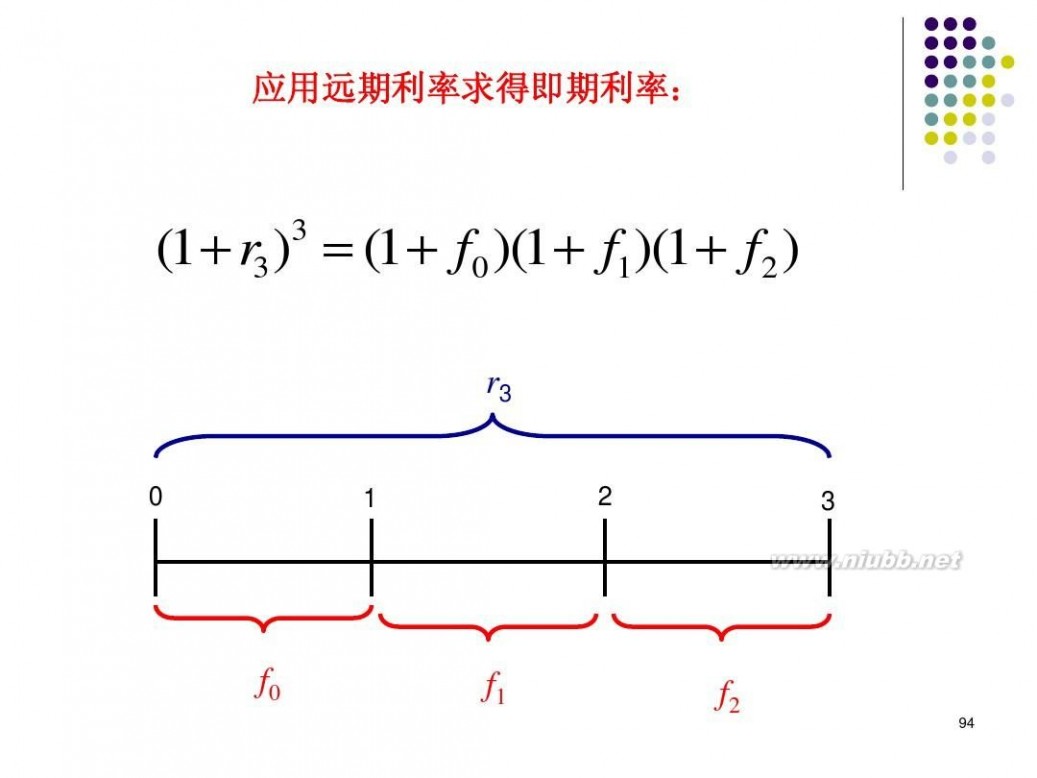
二 : 《金融数学》精算师培训

《金融数学》精算师培训 利率风险 Interest rate risk

1

马考勒久期（Macaulay
?

duration）

假设资产未来的一系列现金流为 Rt ，则资产的价格：

P ? ? Rt ?1 ? i ? ? ? Rt vt
?t t ?0 t ?0

?

实际收益率 i 也可以用名义收益率 i(m)和利息力表示，故：

? i ? (1 ? i ) ? ?1 ? ? e? t ? m ? ?
(m) t

mt

? i ? ? P ? ? Rt ?1 ? ? m ? t ?0 ?
(m)

? mt

? ? Rt e?? t
t ?0
2

资产的价格：

? i ? P ? ? Rt ?1 ? ? m ? t ?0 ?
(m)

? mt

? ? Rt e?? t
t ?0

?

为简化表述，用 y 表示名义收益率，当 m =1时，y就是实 际收益率。

?

未来现金流为 Rt 的资产的价格可以表示为

y? ? P ? ? Rt ?1 ? ? ? m? t ?0

? mt

? ? Rt e?? t
t ?0
3

?

马考勒久期：未来现金流到期时间的加权平均值，权数

为每个现金流的现值在总现值中所占的比率，即：

MacD ?
?

t ? Rt e ?? t ?
t ?0

P

y? ? ? t ? Rt ?1 ? m ? ? ? ? t ?0 P

? mt

马考勒久期越大，加权到期时间越长，从而资产价格对

收益率的敏感性越高，资产的利率风险越大。
?

马考勒久期是一个时间概念，可以用年、月等时间单位 计量。

4

例：一笔贷款的本金为L，期限为n，年实际利率为y，按年
等额分期偿还。试求该笔贷款的马考勒久期。 解： 假设每年末的偿还金额为R

MacD ?

? tR ?1 ? y ?
t ?0

?t

? R ?1 ? y ?
t ?0

?t

?

? t ?1 ? y ?
t ?1 n

n

?t

? ?1 ? y ?
t ?1

?t

?

( I a)n | y an | y

5

例：一项15年期按月等额偿还的贷款，每月复利一次的
年名义利率为24％，试计算这项贷款的马考勒久期。 解：应用上例的结果

MacD ?

( I a) n | y an | y

?

( I a)12?15|0.02 a12?15|0.02

45.7554 ? 45.7554 （月）= ? 3.81 （年） 12

6

?

利息力（收益率）对马考勒久期的影响

将马考勒久期对? 求导可得（请检验）

? u ?? u ?v ? uv? ? ? ? v? v2 ?
2

d( MacD) d ? d? d?

? tR e
t ?0 t t ?0

?? t

Rt e?? t ?

? ? ?? t ? ? 2 ?? t ? ?? t ? ? ? ? Rt e ? ? ? t Rt e ? ? ? ? tRt e ? ? ? t ?0 ? ? t ?0 ? ? ? t ?0 2 ? ? Rt e?? t ? ?? ? t ?0 ?

? ? 2 ?? t ? ? t Rt e ? t ?0 ? ?? ?? ? ? Rt e?? t ? ? ? t ?0 ? ? ?

? tR e
t ?0 t t ?0

?? t

Rt e?? t ?

? ? ? ? ? ?

2

? ? ? ? ? ? ?

? ?? 2 （到期时间的方差）

注：马考勒久期是利息力的减函数，利息力越高，风险越小。
7

? 债券到期时间对马考勒久期的影响（一个反例）
久期

10

5

20 0

40

60
到期时间

息票率 r = 5%，收益率 y =15%

注：

用债券的到期时间衡量利率风险可能是不恰当的。
8

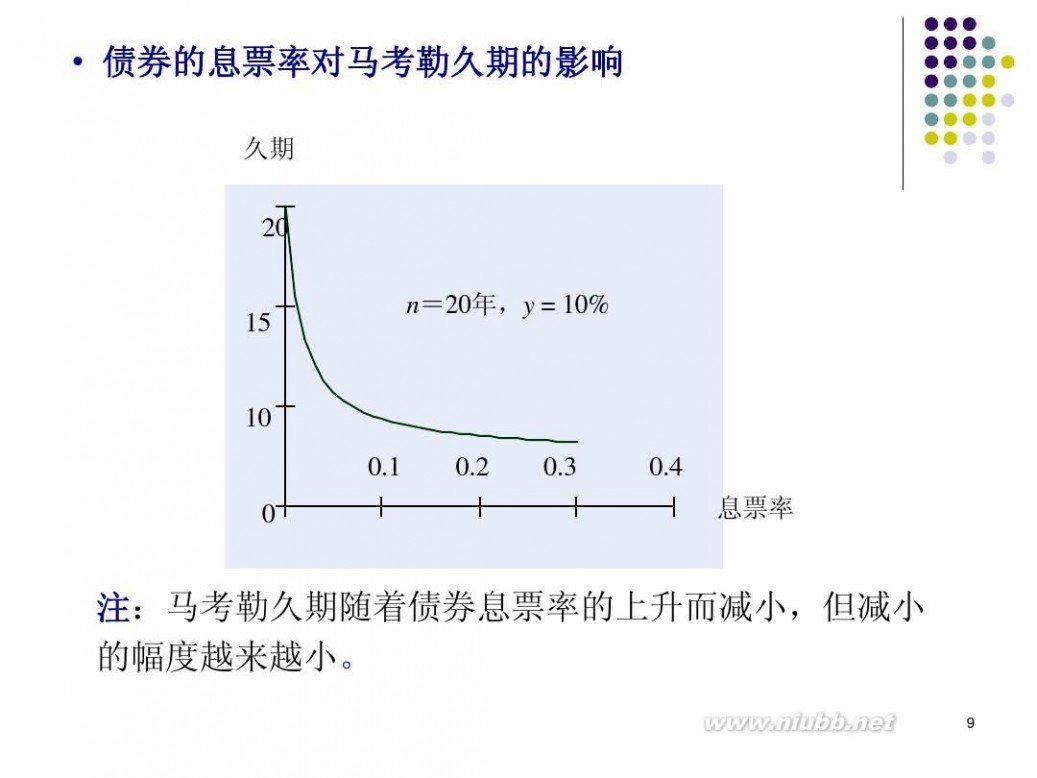
? 债券的息票率对马考勒久期的影响
久期

20
n＝20年，y = 10%

15

10 0.1 0 0.2 0.3 0.4
息票率

注：马考勒久期随着债券息票率的上升而减小，但减小 的幅度越来越小。
9

修正久期
?

修正久期（modified duration）：收益率变化时资产价格

的单位变化速率。
P?( y ) ModD ? ? P( y )
?

修正久期反映了资产价格随收益率变化而变化的速度：
ModD越大，资产价格的波动幅度越大，资产的利率风 险就越大。 ModD越小，资产价格的波动幅度越小，资产的利率风 险就越小。
10

?

资产价格对收益率y（假设每年复利m次）求导可得：

P?( y ) ?

d ? mt ? mt ?1 ? Rt ?1 ? y / m ? ? ?? tRt ?1 ? y / m ? dy t ?0 t ?0

? ? t ?0

? tR ?1 ? y / m ?
t

? mt

?1 ? y / m ?

MacD ? P( y ) ?? ?1 ? y / m ?
MacD ? ModD ? 1? y / m

11

?

修正久期与马考勒久期的关系：

MacD ModD ? 1? y / m
?

当 m→∞ 时， lim ModD ? MacD
m ??

?

而当m→∞时，名义收益率趋于利息力，即 y → ?，因此
P?( y) P?(? ) MacD ? lim ModD ? lim ? ?? m?? m?? P( y ) P(? )
注：请与前面给出的马考勒久期进行比较。
12

?

资产价格与修正久期的关系：

P?( y ) ModD ? ? P( y )

?

1 dP 1 ?P ModD ? ? ?? P dy P ?y

?

?P %?P ? ? ? ModD ? (?y ) P

注： %△P 表示资产价格变化的百分比。 △y 表示收益率的变化，通常用基点（base points） 表示。一个基点为0.01%。
13

?

例：已知某债券的价格为115.92元，收益率为7.00%，修

正久期为8.37。试计算当收益率上升为7.05%时，该债券
的价格。
?

解：当收益率上升时，债券价格下降的百分比为：

%?P ? ?(?y) ? ModD ? ?(7.05% ? 7%) ? 8.37 ? ?0.42%
?

所以新的债券价格可近似为：

115.92 ? (1 ? 0.42%) ? 115.43

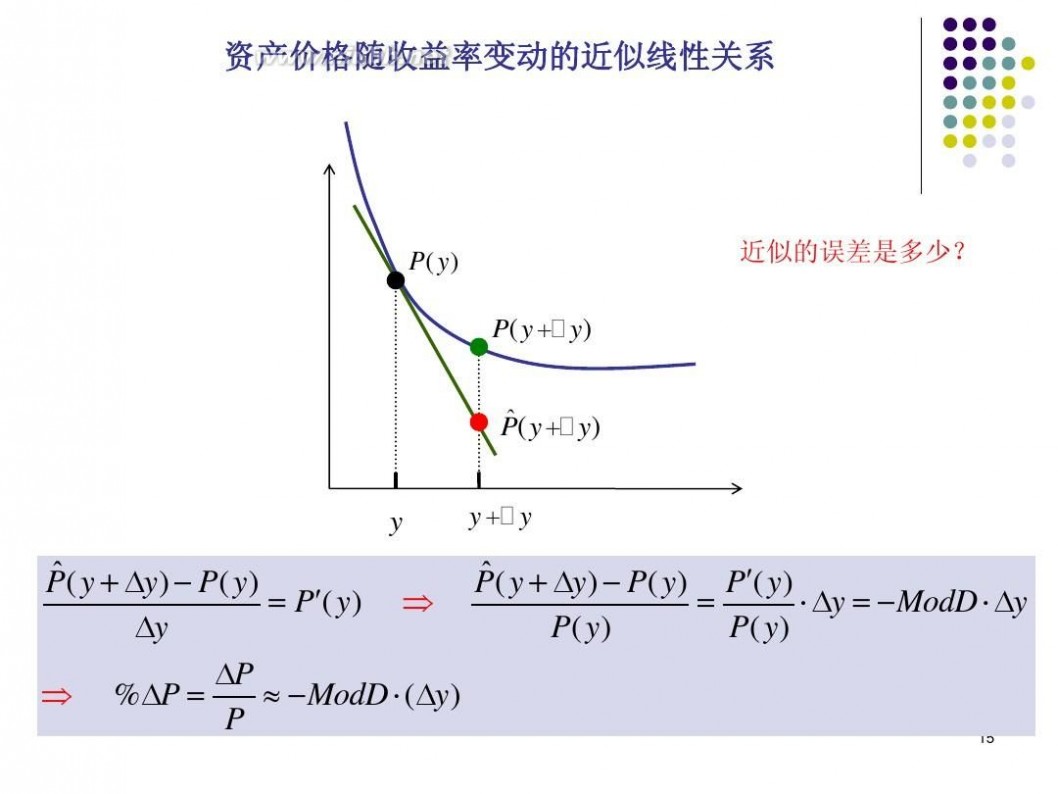
资产价格随收益率变动的近似线性关系

P( y )

近似的误差是多少？
P( y ?? y)

? P( y ?? y)
y ?? y

y

? ? P( y ? ?y ) ? P( y ) P( y ? ?y ) ? P( y ) P?( y ) ? P?( y ) ? ? ? ?y ? ? ModD ? ?y ?y P( y ) P( y ) ?P ? %?P ? ? ? ModD ? (?y ) P 15

有效久期 （effective duration）
?

假定债券未来的现金流是固定的，可以计算债券价格对收益 率的一阶导数P?(y) ，从而可以计算修正久期。

?

如果未来的现金流不是固定的（可赎回债券），可估计 ：
P?( y ) ? P? ? P? 2?y

?

符号： P0 当前收益率下的债券价格

P+
P-

当收益率增加时的债券价格
当收益率减少时的债券价格
16

注：对P?(y)的估计是以割线AB的斜 率来近似在点(y0 ，P0)的切线斜率

P?( y ) ?

P? ? P? 2?y

债券价格随收益率变动的近似线性关系

17

?

如果在修正久期中，用近似值代替P?(y)，则可以得到有

效久期：

P? ? P? P?( y) ModD ? ? ? ? EffD P( y) P0 ? 2?y ?
?

即
P? ? P? EffD ? P0 ? 2?y ?
18

例：已知一个6年期可赎回债券的现价为100元，当收益

率上升100个基点时，该债券的价格将降为95.87元。当收
益率下降100个基点时，该债券的价格将升至104.76元。 试计算该债券的有效久期。 解：

P0 ? 100
P? ? 104.76

P? ? 95.87
?y ? 0.01

P? ? P? 104.76 ? 95.87 EffD ? ? ? 4.45 P0 ? 2?y ? 100 ? 2 ? 0.01
19

凸度 ( convexity )
?

基于名义收益率的凸度C：

P??( y ) C? P( y)
?

修正久期度量了收益率变化时债券价格的稳定性；凸度则

度量了收益率变化时修正久期的稳定性。

P?( y) 修正久期：ModD ? ? P( y )

P??( y) 凸度：C ? P( y )
注：不叫修正凸度
20

债券价格对收益率求二阶导数可得
P?( y ) ? d ? mt ? mt ?1 Rt ?1 ? y / m ? ? ?? tRt ?1 ? y / m ? ? dy t ?0 t ?0
? mt ? 2

y? ? mt ? 1 ? ? P??( y ) ? ? t ? Rt ?1 ? ? ? m ? ? m? t ?0 ?

所以凸度可按下式计算：
- mt - 2 轾 骣 y÷ ⅱy ) P ( 1 犏 1 ? C= = ? 犏 t (t + m ) Rt ?1 + m ÷ ÷ ? 桫 P( y ) P( y ) 犏0 t> 臌

可以证明，凸度是收益率的减函数。
21

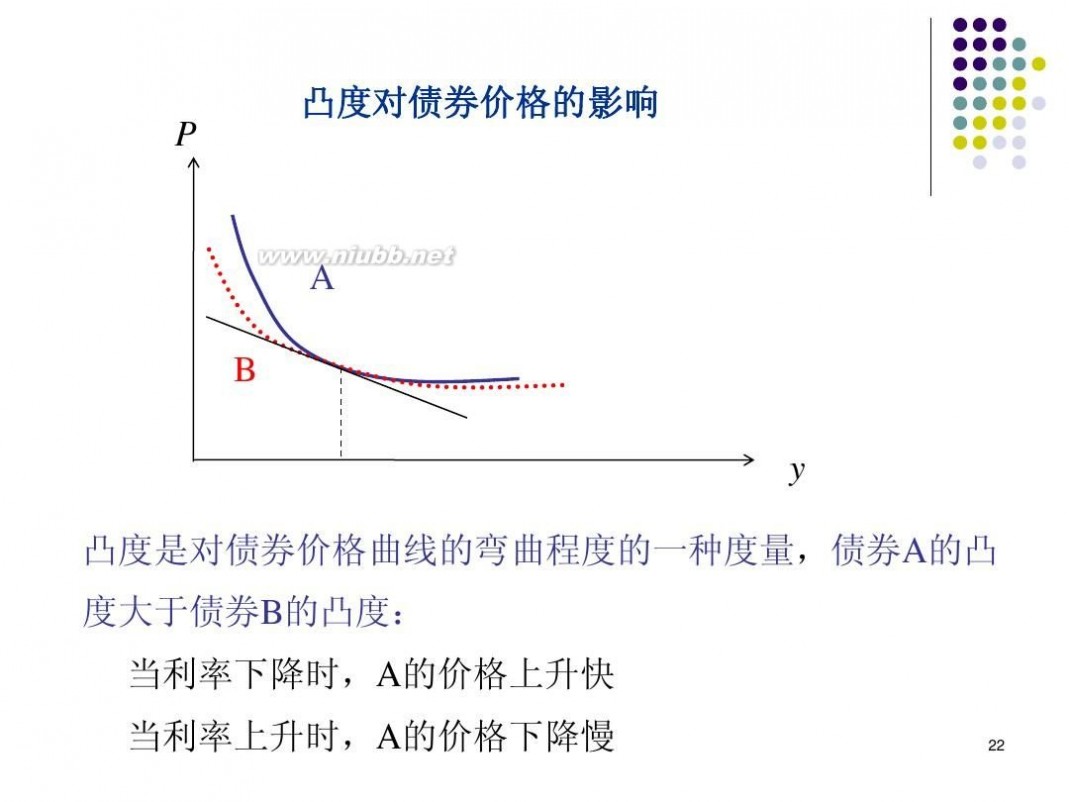
凸度对债券价格的影响 P

A B y 凸度是对债券价格曲线的弯曲程度的一种度量，债券A的凸 度大于债券B的凸度： 当利率下降时，A的价格上升快

当利率上升时，A的价格下降慢

22

马考勒凸度
?用利息力（连续复收益率）?

代替名义收益率 y，即可

得到马考勒凸度：

P??(? ) MacC ? P
d2 ? ?? t ? Rt e ? ? t 2 Rt e ?? t ? d? 2 ? t ?0 ? ? ? t ?0 ? P P

y? ? ? t Rt ?1 ? m ? ? ? ? t ?0 P
2

? mt

e

??

y? ? ? ?1 ? ? ? m?

?m

23

例：一项15年期按月等额偿还的贷款，每月复利一次的年

名义利率为24％，试计算这项贷款的马考勒凸度。
解：y = 24%，m = 12，t = 1/12，2/12，…，15。贷款的现 值为P = 48.5844 而 ? t 2 Rt ?1 ? y ? ? ? ? m? t ?0
? mt

y? ? 2 ? ? t Rt ?1 ? ? ? m? t ?1/12
15

? mt

?

t ?1/12

?

15

t 2 (1.02)?12t

? 1238.91

故

y? ? ? t Rt ?1 ? m ? ? ? MacC ? t ?0 P
2

? mt

1238.91 ? ? 25.50 48.5844
24

?

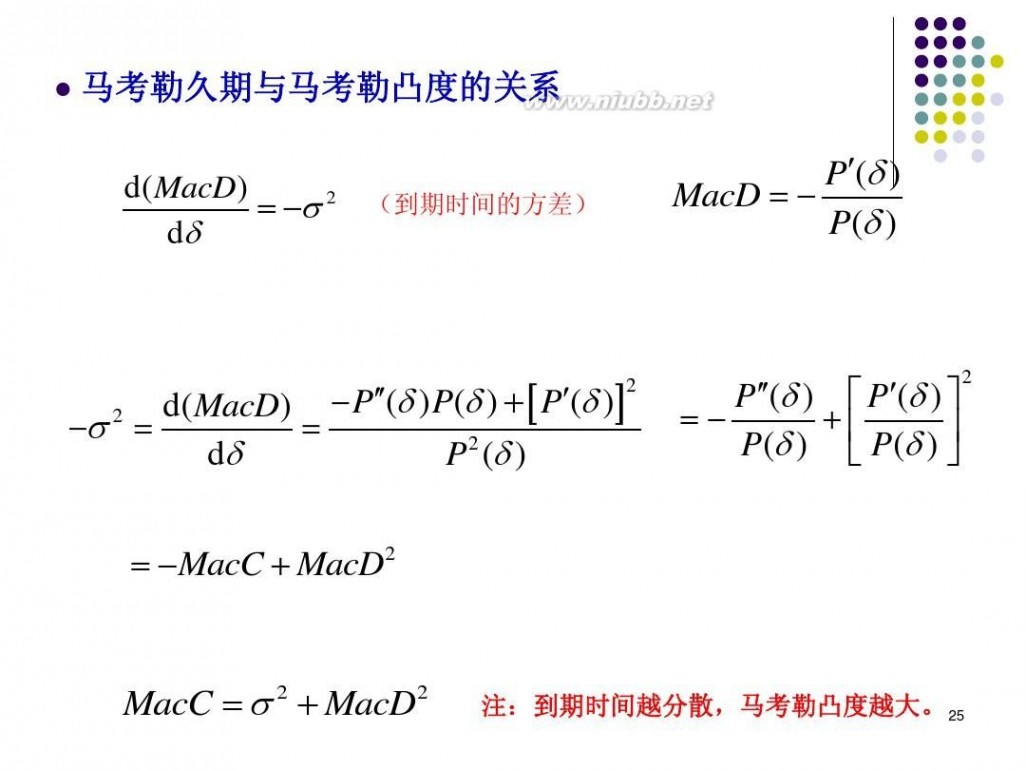
马考勒久期与马考勒凸度的关系
d( MacD) ? ?? 2 d?

（到期时间的方差）

P?(? ) MacD ? ? P(? )

d( MacD) ? P??(? ) P(? ) ? ? P?(? )? ?? ? ? d? P 2 (? )
2

2

P??(? ) ? P?(? ) ? ?? ?? P (? ) ? P (? ) ? ?

2

? ?MacC ? MacD2

MacC ? ? 2 ? MacD2

注：到期

时间越分散，马考勒凸度越大。 25

有效凸度
?

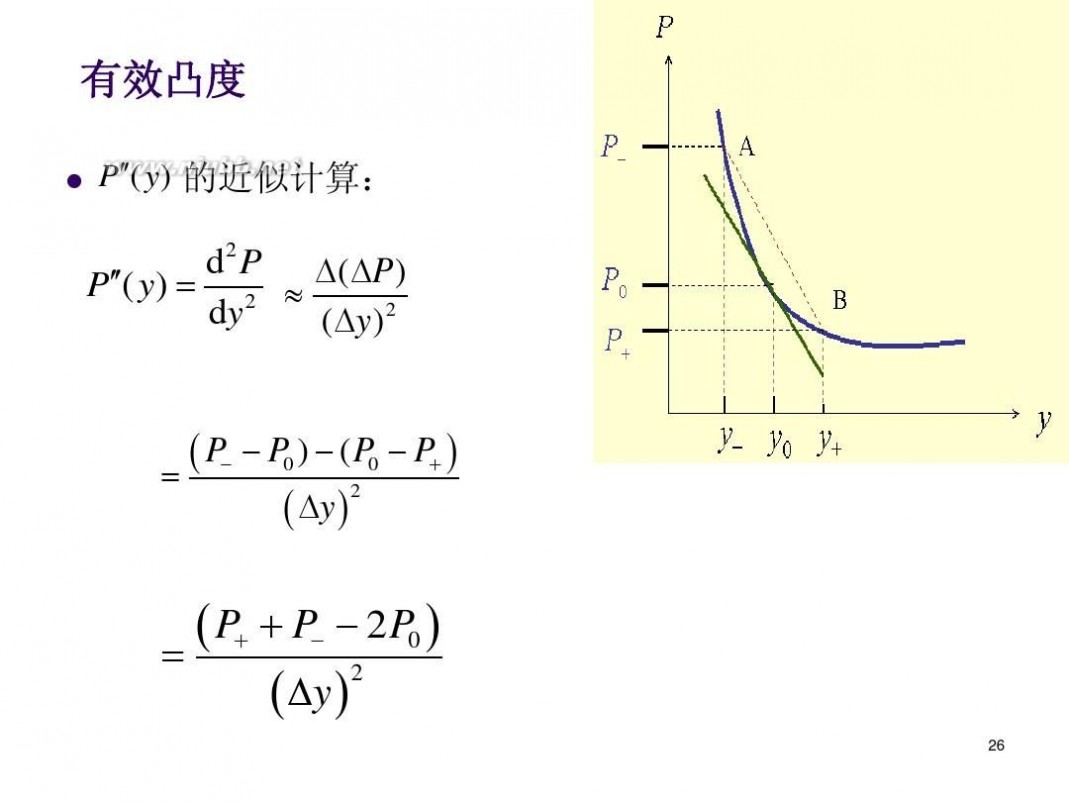
P??( y) 的近似计算：

d 2 P ? ( ?P ) P??( y) ? 2 ? dy ( ?y ) 2

? P? ? P0 ) ? ( P0 ? P? ? ? 2 ? ?y ?

? P? ? P? ? 2 P0 ? ? 2 ? ?y ?
26

?

有效凸度 EffC 是对凸度C的一种近似计算：

P??( y ) ? P? ? P? ? 2 P0 ? C? ? ? EffC 2 P ? ?y ? P0
?

即

? P? ? P? ? 2 P0 ? EffC ? 2 ? ?y ? P0
27

例：已知一个6年期可赎回债券的现价为100元，当收益

率上升100个基点时，该债券的价格将降为95.87元。当收
益率下降100个基点时，该债券的价格将升至104.76元。 试计算该债券的有效凸度。 解：该债券的有效凸度为：

? P? ? P? ? 2 P0 ? ? (95.87 ? 104.76 ? 2 ?100) ? 63 EffC ? 2 2 ? ?y ? P0 ? 0.01? (100)

28

证券组合的久期：
方法一：
计算组合中每种证券的久期

以组合中每种证券的市场价值为权数计算这些久期的
加权平均数。 方法二： 将证券组合设想为一种证券，将证券组合的现金流看 作是设想证券的现金流

根据设想证券的现金流计算久期。
29

例：假设某证券组合由 n 种债券构成，债券 k 具有现值

Pk，

久期Dk，则该证券组合的价格为：

P ? P ? P2 ? ? ? Pn 1
该证券组合的久期为：

? ? ? P? ? ? D P

?P?
k ?1 k

n

P

? P? ? ? ? k ? Pk ? Pk ? n ? ?? ? P k ?1

Pk ? ? Dk k ?1 P

n

类似地，假设债券 k 的凸度为Ck，则证券组合的凸度为：

Pk ?? C ? Ck k ?1 P

n

30

例：一个债券组合由两种面值为100的债券构成，两种债券

到期后均按面值偿还，且年实际收益率均为5%。第一种
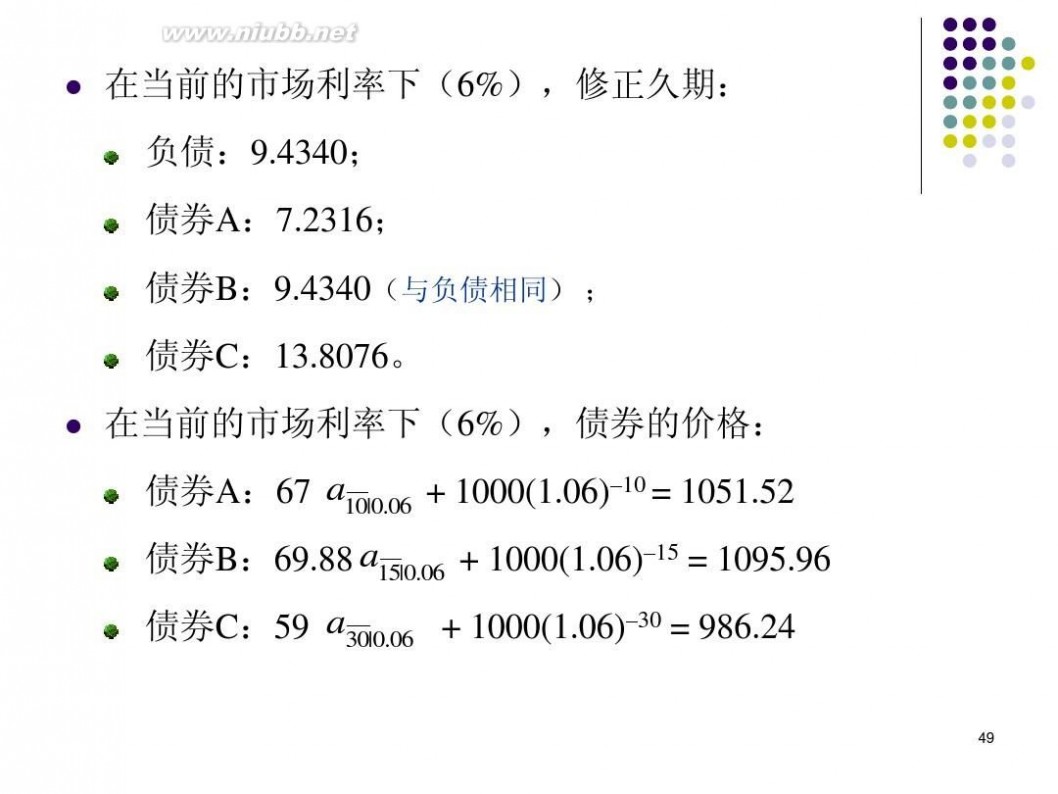
债券的年息票率为6%，期限为5年。第二种债券为10年期 的零息债券。试计算该债券组合的修正久期。 解：第一种债券的价格为

P ? ? Rt ?1 ? y ? 1
t ?1

5

?t

? 6a5 y ? 100(1 ? y ) ?5
? 104.33
31

该债券价格对收益率的一阶导数为：
dP 1 ? dy ?? tRt (1 ? y ) ?t
t ?1 5

1? y
?6 ? Ia ?5 y ? 500(1 ? y ) ?5 1? y

?

? ?444.92

于是第一种债券的修正久期为：
P?( y ) 444.92 ModD1 ? ? 1 ? ? 4.26 P 104.33 1
32

类似地，第二种债券的价格为：

P ? 100(1 ? y)?10 ? 61.39 2
该债券价格对收益率的一阶导数为：
?? tRt (1 ? y ) ?t
t ?1 10

dP2 ? dy

1? y
?1000(1 ? y )?10 ? 1? y
? ?584.68
33

于是第二种债券的修正久期为：
P2?( y) 584.68 ModD2 ? ? ? ? 9.52 P2 61.39

债券组合的价格为：

P ? P ? P2 ? 165.72 1
该债券组合的修正久期为：
P ? P D ? 1 D1 ? 2 D2 ? 6.21 P P
34

小结
价格：

y? ? P ? ? Rt ?1 ? ? ? m? t ?0

? mt

? ? Rt e?? t
t ?0

马考勒久期：

P?(? ) MacD ?

? ? P(? )

t ? Rt e?? t ?
t ?0

P(? )

y? ? ? t ? Rt ?1 ? m ? ? ? ? t ?0 P(? )

? mt

修正久期：

P?( y ) MacD ModD ? ? ? P( y ) 1 ? y / m

有效久期：

P? ? P? EffD ? P0 ? 2?y ?
35

马考勒凸度： MacC

P??(? ) ? ? P(? )

?t
t ?0

2

Rt e

?? t

P(? )

y? ? ? t Rt ?1 ? m ? ? ? ? t ?0 P( y )
2

? mt

凸度：

? mt ? 2 ? ? P??( y ) 1 1 y? ? C? ? ? ? t (t ? ) Rt ?1 ? ? ? P( y ) P( y ) ? t ?0 m ? m? ? ? ?

? P? ? P? ? 2 P0 ? 有效凸度： EffC ? 2 ? ?y ? P0
36

久期和凸度的综合应用
?

将债券的价格函数用泰勒级数展开，则有

P( y) ? P( y0 ) ? P?( y0 )( y ? y0 ) ? 1 P??( y0 )( y ? y0 )2 ? ? ( y ? y0 ) 2
其中 o(y – y0)是关于(y – y0)的高阶无穷小量

?

由此可得近似公式：

?P 1 %?P ? ? ?修正久期 ? (?y ) ? ?凸度 ? (?y ) 2 P 2
37

?P 1 %?P ? ? ?修正久期 ? (?y ) ? ?凸度 ? (?y ) 2 P 2
? ? ? ?

应用上式时，恰当选择久期和凸度： 修正久期和凸度：名义收益率，固定现金流的资产。 马考勒久期和马考勒凸度：利息力，固定现金流的资产。 有效久期和有效凸度：名义收益率，固定现金流的资产或

利率敏感型现金流的资产。

38

例：某债券的面值是1000元，期限为15年，年息票率为11%，到
期时按面值偿还。如果年实际收益率为12%，试计算其价格、 马考勒久期、修正久期和凸度。当年实际收益率上升至12.5%， 债券的价格将如何变化？ 解：

P = 110a15|0.12 + 1000(1+ 0.12)- 15 = 931.89
15 1 ? ?t ?15 ? MacD ? ? ?110? t (1.12) ? 1000 ?15 ? (1.12) ? ? 7.7486 P ? t ?1 ?

ModD ?

MacD 7.7486 ? ? 6.9184 1? y 1.12

15 P??( y) 1 ? ? C? ? ? ?110? t (t ? 1)(1.12)?t ? 2 ? 1000 ? 15 ? 16 ? 1.12?15? 2 ? ? 74.6716 39 P( y ) P ? t ?1 ?

利率上升50个基点所导致的价格变动幅度
? ? ?

真实值：–3.3674%。 用修正久期作近似计算：–6.9184×0.5% = –3.4592% 考虑凸度的影响，凸度引起的价格变化为
1 2

? C ? (?y)2 ? 1 ? 74.6716 ? (0.5%)2 ? 0.0933% 2

?

故市场利率上升50个基点所导致的价格变动幅度为

?3.4592% ? 0.0933% ? ?3.3659%

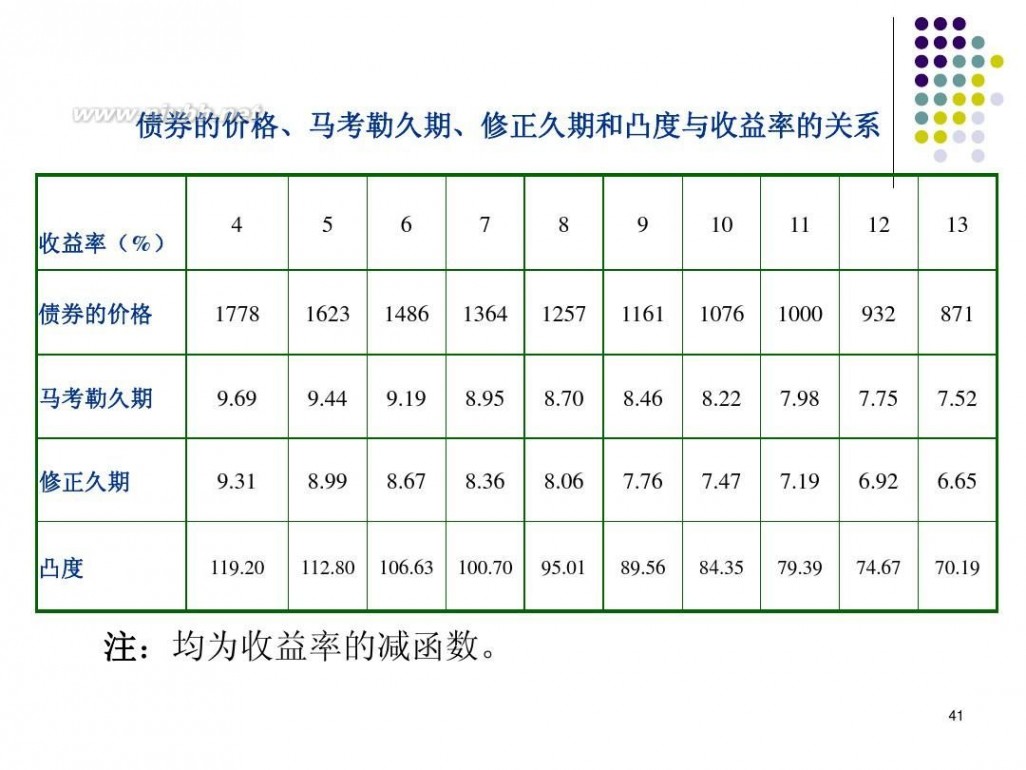
债券的价格、马考勒久期、修正久期和凸度与收益率的关系

收益率（%） 债券的价格

4

5

6

7

8

9

10

11

12

13

1778

1623

1486

1364

1257

1161

1076

1000

932

871

马考勒久期

9.69

9.44

9.19

8.95

8.70

8.46

8.22

7.98

7.75

7.52

修正久期

9.31

8.99

8.67

8.36

8.06

7.76

7.47

7.19

6.92

6.65

凸度

119.20

112.80

106.63

100.70

95.01

89.56

84.35

79.39

74.67

70.19

注：均为收益率的减函数。
41

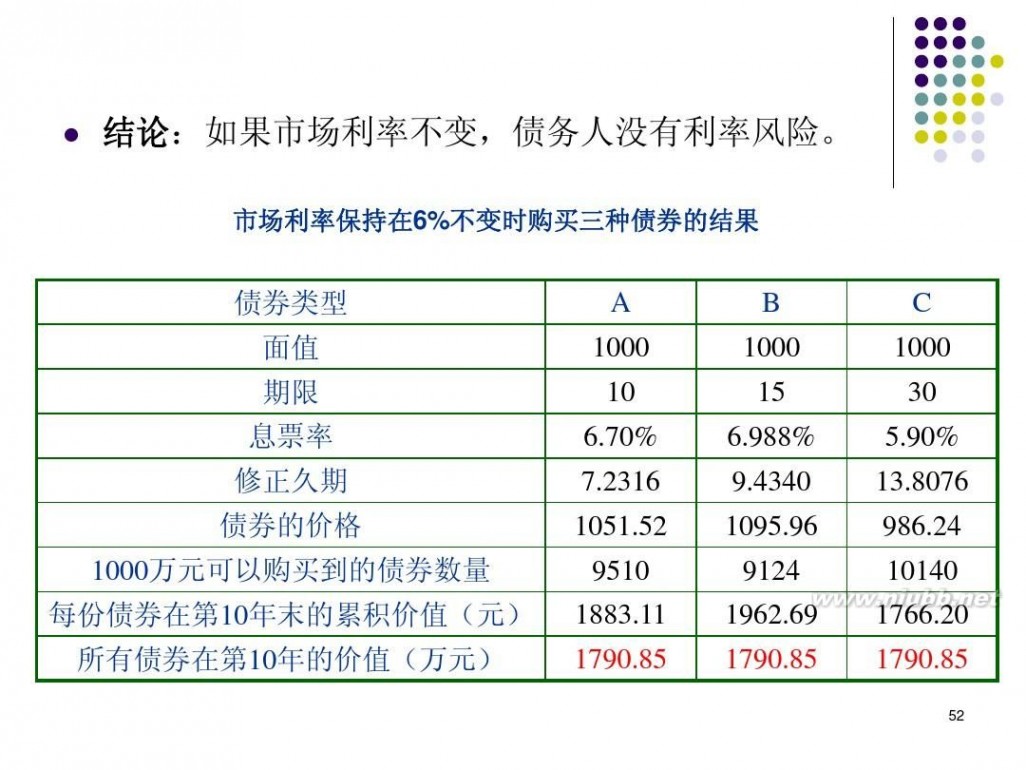
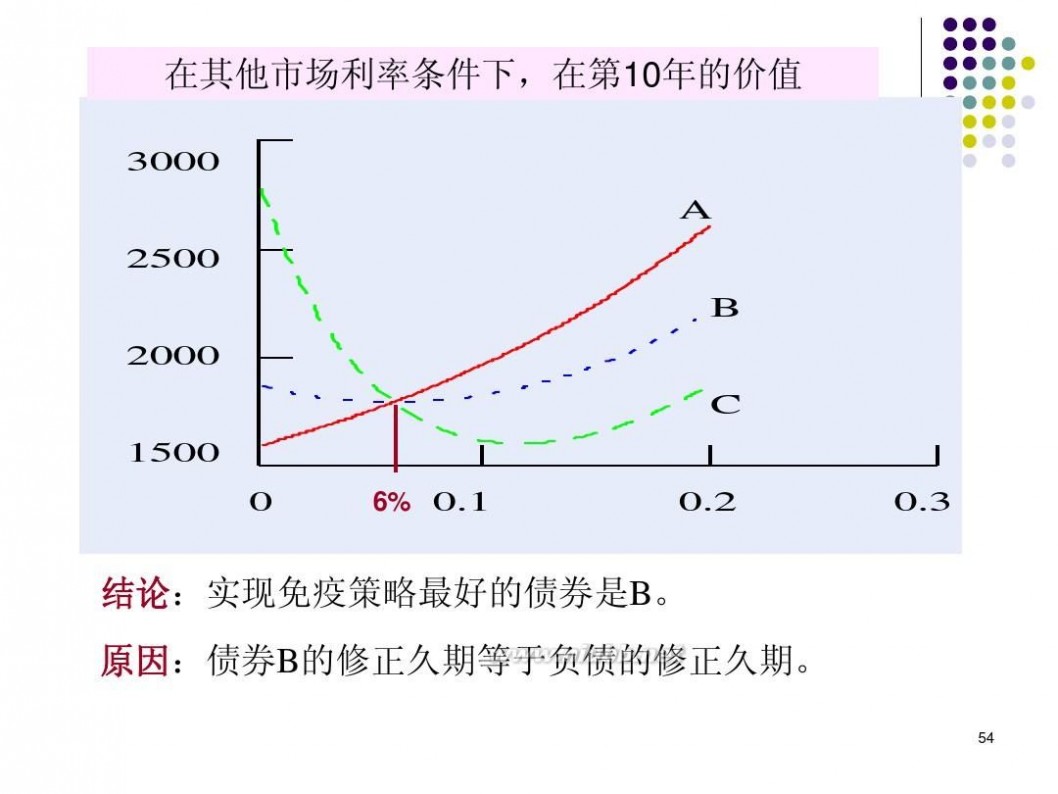
免疫（immunization）

本文标题：精算师培训-《金融数学》精算师培训
本文地址： http://www.61k.com/1110111.html