一 : 在阅览室里 (故事续写）

阅览室里，我正津津有味地看着新书《猪八戒上月球》。太精彩了！我刚想仰头大笑，一看周围，赶紧捂住了嘴巴，尽力不使自己笑出来。“嚓--”急忙中不小心把新书封面撕成了两半。我傻了眼，这可怎么办呢？
我又是害怕又是紧张，生怕被别人看见，于是我用自己的衣服把那本书盖上，然后环顾四周，见没有其他人看见，就急急忙忙把书还回了原处。我又找了一本其他的书看，当我看了一会书的时候，我突然发觉这么做不是我以前的作风，于是我又回到我放书的地方，结果发现那本书已经不见了踪影。我急的像热锅上的蚂蚁，害怕是这里的管理员看见了被我撕坏的书，在到处找我呢。于是我就在整个图书馆里找那本书，找了半天终于发现它在一个小女孩手上，她看见我走近就说：“你也想看吗？如果你想看那你就先拿去看吧.”我心里大喜，心想终于找到了。我拿着书连忙跑到图书管理员那里，把书交给他向他说明了事情经过并道歉，没想到管理员不但没有批评我反而表扬我说：”你真是一个诚实的孩子.”
这件事情让我懂得了：诚信无价，诚实比金钱更加的宝贵和珍贵！

二 : 某同学在A、B两家超市发现他看中的英语学习机的单价相同，书

某同学在A、B两家超市发现他看中的英语学习机的单价相同，书包单价也相同，英语学习机和书包单价之和是452元，且英语学习机的单价比书包单价的4倍少8元。 （1）求该同学看中的英语学习机和书包单价各是多少元？ （2）某一天该同学上街，恰好赶上商家促销，超市A所有商品打7.5折销售；超市B全场购物满100元返购物券30元销售（不足100元不返券，购物券全场通用），但他只带了400元钱，如果他只在一家超市购买看中的英语学习机、书包，那么在哪一家购买更省钱？

题型：解答题难度：中档来源：期末题

解：（1）设书包的单价为x元，则英语学习机的单价为(4x-8)元。 根据题意，得4x-8+x=452 解得x=92 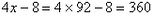答：该同学看中的英语学习机单价为360元，书包单价为92元。 （2）在超市A购买英语学习机与书包各一件，需花费现金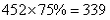：（元）； 因为339<400，所以可以选择超市A购买。 在超市B可先花费现金360元购买英语学习机，再利用得到的90元购物券，加上2元现金购买书包，总计共花费现金：360+2=362（元）； 因为362<400，所以也可以选择在超市B购买。 但是，由于362>339，所以在超市A购买英语学习机与书包，更省钱。

考点：

考点名称：一元一次方程的应用许多实际问题都归结为解一种方程或方程组，所以列出方程或方程组解应用题是数学联系实际，解决实际问题的一个重要方面；
同时通过列方程解应用题，可以培养我们分析问题，解决问题的能力。列一元一次方程解应用题的一般步骤：
列方程（组）解应用题是中学数学联系实际的一个重要方面。其具体步骤是：
⑴审题：理解题意。弄清问题中已知量是什么，未知量是什么，问题给出和涉及的相等关系是什么。
⑵设元（未知数）：找出等量关系：找出能够表示本题含义的相等关系；
①直接未知数：设出未知数，列出方程：设出未知数后，表示出有关的含字母的式子，然后利用已找出的等量关系列出方程；
②间接未知数（往往二者兼用）。
一般来说，未知数越多，方程越易列，但越难解。
⑶用含未知数的代数式表示相关的量。
⑷寻找相等关系（有的由题目给出，有的由该问题所涉及的等量关系给出），列方程。一般地，未知数个数与方程个数是相同的。
⑸解方程及检验。
⑹答题。
综上所述，列方程（组）解应用题实质是先把实际问题转化为数学问题（设元、列方程），在由数学问题的解决而导致实际问题的解决（列方程、写出答案）。在这个过程中，列方程起着承前启后的作用。因此，列方程是解应用题的关键。

一元一次方程应用题型及技巧：
列方程解应用题的几种常见类型及解题技巧：
（1）和差倍分问题：
①倍数关系：通过关键词语“是几倍，增加几倍，增加到几倍，增加百分之几，增长率……”来体现。
②多少关系：通过关键词语“多、少、和、差、不足、剩余……”来体现。
③基本数量关系：增长量＝原有量×增长率，现在量＝原有量＋增长量。

（2）行程问题：
基本数量关系：路程＝速度×时间，时间＝路程÷速度，速度＝路程÷时间，
路程=速度×时间。
①相遇问题：快行距＋慢行距＝原距；
②追及问题：快行距－慢行距＝原距；
③航行问题：
顺水（风）速度＝静水（风）速度＋水流（风）速度，
逆水（风）速度＝静水（风）速度－水流（风）速度
例：甲、乙两站相距480公里，一列慢车从甲站开出，每小时行90公里，一列快车从乙站开出，每小时行140公里。
慢车先开出1小时，快车再开。两车相向而行。问快车开出多少小时后两车相遇？
两车同时开出，相背而行多少小时后两车相距600公里？
两车同时开出，慢车在快车后面同向而行，多少小时后快车与慢车相距600公里？
两车同时开出同向而行，快车在慢车的后面，多少小时后快车追上慢车？
慢车开出1小时后两车同向而行，快车在慢车后面，快车开出后多少小时追上慢车？ (此题关键是要理解清楚相向、相背、同向等的含义，弄清行驶过程。)
例：一艘船在两个码头之间航行，水流速度是3千米每小时，顺水航行需要2小时，逆水航行需要3小时，求两码头的之间的距离？

（3）劳力分配问题：抓住劳力调配后，从甲处人数与乙处人数之间的关系来考虑。 这类问题要搞清人数的变化。
例.某厂一车间有64人，二车间有56人。现因工作需要，要求第一车间人数是第二车间人数的一半。问需从第一车间调多少人到第二车间？

（4）工程问题：
三个基本量：工作量、工作时间、工作效率；
其基本关系为：工作量=工作效率×工作时间；相关关系：各部分工作量之和为1。
例：一件工程，甲独做需15天完成，乙独做需12天完成，现先由甲、乙合作3天后，甲有其他任务，剩下工程由乙单独完成，问乙还要几天才能完成全部工程？

（5）利润问题：
基本关系：
①商品利润=商品售价-商品进价；
②商品利润率=商品利润/商品进价×100%；
③商品销售额＝商品销售价×商品销售量；
④商品的销售利润＝（销售价－成本价）×销售量。
⑤商品售价=商品标价×折扣率例.
例：一家商店将某种服装按进价提高40%后标价，又以8折优惠卖出，结果每件仍获利15元，这种服装每件的进价是多少？

（6）数字问题：一般可设个位数字为a，十位数字为b，百位数字为c，十位数可表示为10b+a， 百位数可表示为100c+10b+a，然后抓住数字间或新数、原数之间的关系找等量关系列方程。
数字问题中一些表示：两个连续整数之间的关系，较大的比较小的大1；
偶数用2n表示，连续的偶数用2n+2或2n—2表示；奇数用2n+1或2n—1表示。
例：有一个三位数，个位数字为百位数字的2倍，十位数字比百位数字大1，若将此数个位与百位顺序对调（个位变百位）所得的新数比原数的2倍少49，求原数。

（7）盈亏问题：“盈”表示分配中的多余情况；“亏”表示不足或缺少部分。

（8）储蓄问题：
其数量关系是：
利息＝本金×利率×存期；：（注意：利息税）。
本息＝本金＋利息，利息税＝利息×利息税率。
注意利率有日利率、月利率和年利率，年利率＝月利率×12＝日利率×365。

（9）溶液配制问题：
其基本数量关系是：溶液质量＝溶质质量＋溶剂质量；
溶质质量＝溶液中所含溶质的质量分数。
这类问题常根据配制前后的溶质质量或溶剂质量找等量关系，分析时可采用列表的方法来帮助理解题意。

（10）比例分配问题：
这类问题的一般思路为：设其中一份为x，利用已知的比，写出相应的代数式。
常用等量关系：各部分之和＝总量。
还有劳力调配问题、配套问题、年龄问题、比赛积分问题、增长率问题等都会有涉及。

三 : 真事求过！ 今天刚刚期中考试完 走出教室在操场上看见一个同学 于是跑去

真事求过！ 今天刚刚期中考试完，走出教室在操场上看见一个同学，于是跑去问他考的怎么样..想必他也是段中人！抬头45度仰望天空眼神犀利地说：这样说吧.....还没说完天上一坨鸟屎落他脸上！！笑得我一个下午都合不拢嘴！ 顶高点！让他看见！！

四 : 在阅览室里续写

　　阅览室里，我正津津有味地看着新书《猪八戒上月球》。太精彩了！我刚想仰头大笑，一看周围，赶紧捂住嘴巴，尽力不使自己笑出声来。“嚓——”急忙中，不小心把新书的封面撕成了两半。我傻了眼，这可怎么办呢？
　　我心里又急又怕，生怕服务员阿姨打电话给我爸爸，让他赔书钱，爸爸付完钱肯定要骂我，这可怎么办？我抬头看见服务员正朝我走来，我便急忙合上书，走向书柜，把那本新书塞进书柜便跑开了。过了一会儿，我认为自己的行为很不诚实，决定去向图书馆阿姨道歉。
　　我走到书柜前，看见那个阿姨正在用胶带修补我看的那本书叹气的说：“哎，又有新书被撕坏了。”我惭愧的低着头，对阿姨说：“对不起阿姨，这本书是撕坏的，我来赔吧！”“不、不小同学，不用你赔了，你很诚实也很勇敢，是我见过最善良的同学！”阿姨笑着对我说。
　　通过这件事，让我知道——诚实是最重要的！

本文标题：在阅览室看书的同学中-在阅览室里 (故事续写）
本文地址： http://www.61k.com/1093527.html