一 : 定义D(a,b)=表示数轴上a,b两数对应点间的距离.①分别
定义D(a,b)=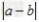 表示数轴上a,b两数对应点间的距离. 表示数轴上a,b两数对应点间的距离.①分别求D(0,﹣3),D 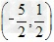 的值; 的值;②若D(1,x)=2,求x的值; ③若数轴上不同的三点所表示的数m,n,z满足D(m,n)=D(m,z)+D(z,n),试说明m,n,z的大小关系. |
解:①D(0,﹣3)= =3;D =3;D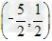 = = =3; =3;②D(1,x)= 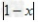 ,由已知 ,由已知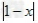 =2,得x=﹣1或3; =2,得x=﹣1或3;③m<z<n或n<z<m. |
考点:
考点名称:代数式的求值 代数式的值:数轴的应用范畴:
符号相反的两个数互为相反数,零的相反数是零。(如2的相反—2)
在数轴上离开原点的距离就叫做这个数的绝对值。一个正数的绝对值是它本身,一个负数的相反数是它的正数,0的绝对值是0。
绝对值的有关性质:
①任何有理数的绝对值都是大于或等于0的数,这是绝对值的非负性;
②绝对值等于0的数只有一个,就是0;
③绝对值等于同一个正数的数有两个,这两个数互为相反数;
④互为相反数的两个数的绝对值相等。
绝对值的化简:
绝对值意思是值一定为正值,按照“符号相同为正,符号相异为负”的原则来去绝对值符号。
①绝对值符号里面为负,在去掉绝对值时必须要加一个负的符号老确保整个值为正值,也就是当:
│a│=a (a为正值,即a≥0 时);│a│=-a (a为负值,即a≤0 时)
②整数就找到这两个数的相同因数;
③小数就把这两个数同时扩大相同倍数成为整数,一般都是扩大10、100倍;
④分数的话就相除,得数是分数就是分子:分母,要是得数是整数,就这个数比1。
二 : 论数与数轴上点的对应关系
摘要:数,表示事物的量的基本数学概念,是数学讨论的基本元素。而轴(形数)是规定了原点、方向、长度单位的直线(点的集合)。两者有机结合,形成一种数学思想――数形结合思想。化数为形,化形为数,给抽象的概念予以直观的表述,可使复杂问题简单化、抽象问题具体化。
关键词:数;数轴;对应关系
中图分类号:G712 文献标志码:A 文章编号:1674-9324(2014)12-0231-02
现实的中等职业学校,学生一般基础较差。本人通过多年的中职数学教学,深知学生在数学课程中经常用到的“实数与数轴上的点一一对应”这一普遍而常用的结论,在不等式解集的表示,集合的有关运算中时常出现错误。下面谈一谈“实数与数轴”的内在联系。
一、自然数
1.(基数理论)两个可以在元素之间建立一一对应关系的有限集具有共同的数量特(www.61k.com)征,这一特征叫做基数。这样,所有单元素集{x},{y},{a},{b}等具有同一基数,记作1。类似,凡能与两个手指头建立一一对应的集合,如{x.Y},{a,b}它们的基数相同,记作2,等等,即基数是指集合中元素的“个数”。
2.(序数理论)在自然数集N中有:(1)N中存在元素“1”,它不是N中任何一个元素的后继数.(2)N中每一个元素有且只有一个后继数。由此可知N中的元素可按1,2,3,4…这样的顺序排列。
在集合中,空集不含任何元素,只能用“0”来描述空集中所含元素的多少。因此,无论从自然数的序数功能方面把0作为自然数,还是在自然数的运算功能(见后自然数性质3)中把0作为自然数,都有理由说得过去,正因为如此,我国中小学教材将0化归为自然数系列。自然数的基本性质有:(1)有最小元素0,没有最大元素但是有顺序。(2)无限集。(3)具有离散性(对任意两个相连自然数之间不存在第三个自然数。(4)对加法,乘法运算都是封闭的,即集合{0,1,2,3,4,5,…,n,…}中的任何两个自然数都可以进行加法和乘法运算,而运算结果仍然是自然数。数轴是人为规定的,满足有:(1)原点。(2)长度单位。(3)正方向的几何图形(点的集合)。从原点(记为0)出发朝正方向(右)的直线上取适当的长度作为单位长度,比如可以取1cm作为单位长度,这样距起点零一个长度单位的点就对应数1,距零两个长度单位的点就对应数2,依次类推。这样每个自然数(又称正整数)就在数轴上与相应的点形成数对点的一一对应,这些点称为自然数点,基于自然数的离散性,使得点与点之间没有相连,是孤立的,自然数与轴上点就结合在一起。
二、整数
生活中有很多具有相反意义的现象,比如增加和减少、前进和后退等。既然有相反意义的现象,那么记录这两者的数字符号也应有区别。于是引入了负数概念,负数是人们记录具有相反意义现象的不同数字符号,由于每一个正数(自然数)都有它相对的一个负数,它们对称的分布在轴原点的两边,这样的一对数互称为相反数(若a=-b则a是b的相反数)。我们把与自然数相对的原点左边的这类数称为负整数。正整数、零与负整数构成了整数系(Z)。整数系是自然数系的扩展,自然数的一切性质整数都具有,但同时也有自然数不具备的性质(后有说明)。整数系虽是无限集合,但它并不是密密麻麻地分布在整个图上,而是间隔分布。
事情并没有结束,上述的整数点与整数点之间仍有间隙,那么这之间的点又如何解读呢?这就使人们又联想到在整数点与点之间一定还有另外的(点)数存在。我们知道,自然数系是一个离散的、而不是稠密的数系,作为量的表征,它只能限于去表示一个单位量的整数倍,而无法表示它的部分。同时,作为运算的手段,在自然数系中只能施行加法和乘法,而不能自由地施行它们的逆运算。因此把自然数系扩大到整数系后,加法,减法,乘法总可以施行。但除法又不能自由施行,即两个数的商不一定是整数。如求解方程mx=n(m≠0),如果m,n是整数,则方程不一定有整数解。为了使它恒有解,解决这一问题的有效方法就是把整数系再扩大。事实上人类可知的量,除了能表示个体的量(整数)之外。另一类是可无限细分的量(如长度,面积)。对于能无限细分的量,用一个可相比的数来表示。
三、有理数
有理数就是可以用比来表示的数,常用(m∈Z。n∈N*)形式表示,故又称作分数。这类数有如下性质:(1)加法,减法,乘法,除法(除数不为零)运算总可实施,即运算的结果总是有理数(有理数的封闭性)。(2)任意两个有理数都可以比较大小(顺序性)。(3)有理数集具有稠密性。即对任意两个有理数a 和b,总有一个有理数c满足a
远在两千多年前的古希腊,有一个专门研究数学的团体。他们画了一个边长为1的正方形,根据勾股定理来求其对角线长度,但这对角线的长度不知道用一个怎样的数来表示,但这个数又肯定是存在的,最后认定这是一个从未见过的新数。受这个数的启示,后来又陆续发现了很多都与上述对角线长度数具有一样共性的数,人们把这些数取名为无理数。诸如开方开不尽的数,,等。大多数三角函数值(如sin50°),对数函数值,计算中产生的数( π,e)以及构造出来的无理数(0.1010010001…)等。因此,无理数集也是无限集,既没有最大的元素,也没有最小的元素。这样的一些数,在数轴上同样能够找到这样的点与之对应。
有理数和无理数统称为实数。实数具有下列性质:(1)在实数集中,加法,减法。乘法。除法(除数不为零)运算总可以实施。(2)任意两个实数都可以比较大小。(3)实数集具有稠密性,对任意两个实数α<β存在一个实数γ,使得α<γ<β。(4)实数集具有连续性。
综上所述,数轴上的点除了有理点之外,都是无理点,且每个有理数和无理数在数轴上都能找到对应的点。所有的实数布满了整个数轴。正是实数集具有连续的特性,使得实数点布满了整个数轴。实数与数轴上的点一一对应,直线可以看作是实数的几何表示。讨论实数的性质就可在直线上进行,这就为后来的实数理论的应用提供了理论基础。试想,如学生掌握了这些知识,势必对数轴的应用能得心应手,起到事半功倍的作用。
三 : 与数轴上的点一一对应的数是().
| 与数轴上的点一一对应的数是( ). |
| 实数. |
考点:
考点名称:数轴数轴定义:数轴的应用范畴:
符号相反的两个数互为相反数,零的相反数是零。(如2的相反—2)
在数轴上离开原点的距离就叫做这个数的绝对值。一个正数的绝对值是它本身,一个负数的相反数是它的正数,0的绝对值是0。
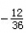 )和无理数(如π、
)和无理数(如π、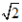 )两类,或代数数和超越数两类,或正数,负数和零三类。
)两类,或代数数和超越数两类,或正数,负数和零三类。实数的性质:
1.基本运算:
实数可实现的基本运算有加、减、乘、除、平方等,对非负数还可以进行开方运算。
实数加、减、乘、除(除数不为零)、平方后结果还是实数。
任何实数都可以开奇次方,结果仍是实数,只有非负实数,才能开偶次方其结果还是实数。
有理数范围内的运算律、运算法则在实数范围内仍适用:
交换律:a+b=b+a , ab=ba
结合律:(a+b)+c=a+(b+c)
分配律:a(b+c)=ab+ac
2.实数的相反数:
实数的相反数的意义和有理数的相反数的意义相同。
实数只有符号不同的两个数,它们的和为零,我们就说其中一个是另一个的相反数。
实数a的相反数是-a,a和-a在数轴上到原点0的距离相等。
3.实数的绝对值:
实数的绝对值的意义和有理数的绝对值的意义相同。一个正实数的绝对值等于它本身;
一个负实数的绝对值等于它的相反数,0的绝对值是0,实数a的绝对值是 :|a|
①a为正数时,|a|=a(不变)
②a为0时, |a|=0
③a为负数时,|a|= a(为a的相反数)
(任何数的绝对值都大于或等于0,因为距离没有负的。)
4实数的倒数:
实数的倒数与有理数的倒数一样,如果a表示一个非零的实数,那么实数a的倒数是:1/a (a≠0)
实数的分类:
(1)按定义分类:
正整数
整数{ 零
负整数
有理数{ }有限小数或无限循环小数
真分数
分数{
实数{负分数
正无理数
无理数{ }无限不循环小数
负无理数
(2)按性质分类:
正整数
正有理数{
正实数{ 正分数
正无理数
实数{ 零 负整数
负有理数{
负实数{负分数
负无理数
四 : 下列命题中错误的是()A.数轴上的点与有理数是一一对应的
下列命题中错误的是( )
|
| A、数轴上的点与实数是一一对应关系,有理数只是实数的一部分,故本选项错误; B、符合实数与数轴的关系,故本选项正确; C、因为数轴上的点与实数是一一对应关系,无理数只是实数的一部分,所以无理数都可以用数轴上的点表示,故本选项正确; D、符合平面直角坐标系内点的坐标特点,故本选项正确. 故选A. |
考点:
考点名称:数轴数轴定义:数轴的应用范畴:
符号相反的两个数互为相反数,零的相反数是零。(如2的相反—2)
在数轴上离开原点的距离就叫做这个数的绝对值。一个正数的绝对值是它本身,一个负数的相反数是它的正数,0的绝对值是0。
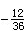 )和无理数(如π、
)和无理数(如π、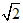 )两类,或代数数和超越数两类,或正数,负数和零三类。
)两类,或代数数和超越数两类,或正数,负数和零三类。实数的性质:
1.基本运算:
实数可实现的基本运算有加、减、乘、除、平方等,对非负数还可以进行开方运算。
实数加、减、乘、除(除数不为零)、平方后结果还是实数。
任何实数都可以开奇次方,结果仍是实数,只有非负实数,才能开偶次方其结果还是实数。
有理数范围内的运算律、运算法则在实数范围内仍适用:
交换律:a+b=b+a , ab=ba
结合律:(a+b)+c=a+(b+c)
分配律:a(b+c)=ab+ac
2.实数的相反数:
实数的相反数的意义和有理数的相反数的意义相同。
实数只有符号不同的两个数,它们的和为零,我们就说其中一个是另一个的相反数。
实数a的相反数是-a,a和-a在数轴上到原点0的距离相等。
3.实数的绝对值:
实数的绝对值的意义和有理数的绝对值的意义相同。一个正实数的绝对值等于它本身;
一个负实数的绝对值等于它的相反数,0的绝对值是0,实数a的绝对值是 :|a|
①a为正数时,|a|=a(不变)
②a为0时, |a|=0
③a为负数时,|a|= a(为a的相反数)
(任何数的绝对值都大于或等于0,因为距离没有负的。)
4实数的倒数:
实数的倒数与有理数的倒数一样,如果a表示一个非零的实数,那么实数a的倒数是:1/a (a≠0)
实数的分类:
(1)按定义分类:
正整数
整数{ 零
负整数
有理数{ }有限小数或无限循环小数
真分数
分数{
实数{负分数
正无理数
无理数{ }无限不循环小数
负无理数
(2)按性质分类:
正整数
正有理数{
正实数{ 正分数
正无理数
实数{ 零 负整数
负有理数{
负实数{负分数
负无理数
 ;点P(x,y)在第二象限
;点P(x,y)在第二象限
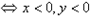 ;点P(x,y)在第四象限
;点P(x,y)在第四象限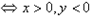
 y=0,x为任意实数
y=0,x为任意实数 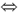 x=0,y为任意实数
x=0,y为任意实数  x,y同时为零,即点P坐标为(0,0)。
x,y同时为零,即点P坐标为(0,0)。  。 坐标表示位置步骤:
。 坐标表示位置步骤:61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1