一 : 某大草原上有一条笔直的公路,在紧靠公路相距40千米的A,B两地,分别有甲,乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C.一天,甲医疗队接到牧民区的求救电话,立刻设计了两种救助方案.
某大草原上有一条笔直的公路,在紧靠公路相距40千米的A,B两地,分别有甲,乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C.一天,甲医疗队接到牧民区的求救电话,立刻设计了两种救助方案.
方案I:从A地开车沿公路到离牧民区C最近的D处,再开车穿越草地沿DC方向到牧民区C.
方案II:从A地开车穿越草地沿AC方向到牧民区C.已知汽车在公路上行驶的速度是在草地上行驶速度的3倍.
(1)求牧民区到公路的最短距离CD;
(2)你认为甲医疗队设计的两种救助方案,哪一种方案比较合理?并说明理由.(结果精确到0.1,参考数据:根号3取1.73,根号2取1.41)
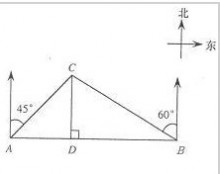
因为AB=40,依题可得AD=CD,可设AD为x,则CD=x,DB=40-x;
1、又因为角CBD=30度;所以CD/BD=tan30
所以可得x/(40-x)=1.73/3,所以计算可得x=14.7
所以CD=14.7
2、设汽车在草地上行驶的速度为一个单位,则汽车在公路上行驶的速度为3个单位;
依上题可计算AC=20.7,所以方案II从AC走的时间为20.7
而方案I从AD,CD方向走的时间为2*14.7/3=9.8
可以看到20.7远远大于9.8,即从方案II走所用的时间远远方案I
所以选择方案I比较合理
二 : 行程问题AB两地相距480千米甲乙两辆大巴同时从AB两地出发经过
行程问题
AB两地相距480千米甲乙两辆同时从AB两地出发经过4.5小时两车相遇后又相距120千米这时甲乙两车路程比是8:7,问甲乙两辆车各行多少多少千米?
甲车行(480+120)*8/(8+7)=320千米,
乙车行(480+120)*7/(8+7)=280千米.
三 : 比例尺应用题在一副比例尺是1:的地图上,量得甲乙两地放入距离是1
比例尺应用题
在一副比例尺是1: 的上,量得甲 乙两地放入距离是10厘米,在一列客车和一列货车同时从甲乙两地相向而行,3小时相遇,已知客车和货车的速度比是3:2,货车每小时行多少千米?客车再行驶几小时后到达甲地?
两地相距:10÷1/7500000=75000000厘米=750千米
相遇时,货车行的路程是:750÷(3+2)×2=300千米
货车每小时行:300÷3=100千米
客车速度为:100÷2×3=150千米
客车还需行750÷150-3=2小时
四 : 甲乙两地相距360km,新修的高速公路开通后,在甲
| 甲乙两地相距360km,新修的高速公路开通后,在甲乙两地行驶的汽车的平均速度提高了50%,而从甲地到乙地的时间缩短了2h.求汽车提速后的平均车速? |
| 设提速前的平均车速为xkm/h,(1分) 根据题意得:
解得:x=60(1分) 经检验:x=60是原方程的解,(1分) 所以,(1+50%)x=90(km/h) 答:汽车提速后的平均车速为90km/h.(1分) |
考点:
考点名称:分式方程的应用列分式方程解应用题和列整式方程解应用题步骤基本相同,但必须注意,要检验求得的解是否为原方程的根,以及是否符合题意。
列分式方程解应用题的一般步骤是:
①找等量关系(审):理解题意,弄清具体情境中的已知量与未知量以及它们之间的基本关系;
②设:设未知数,用含x(或其他字母)表示某个未知数,由该未知数与其他数量的关系,写出表示相关量的式子;
③列:找出相等关系,列出分式方程;
④解:解这个分式方程;
⑤检验:双重检验,先检验是否为增根,再检验是否符合题意;
⑥答:写出答案。
例题
南宁到昆明西站的路程为828KM,一列普通列车和一列直达快车都从南宁开往昆明。直达快车的速度是普通快车速度的1.5倍,普通快车出发2H后,直达快车出发,结果比普通列车先到4H,求两次的速度.
设普通车速度是x千米每小时则直达车是1.5x
由题意得:
828/x-828/1.5x=6 ,
(828×1.5-828)/1.5x=6 ,
414/1.5=6x,
x=46, 1.5x=69
答:普通车速度是46千米每小时,直达车是69千米每小时。
无解的含义:
1.解为增根。
2.整式方程无解。(如:0x不等于0.)
用分式解应用题的常见题型:
(1)行程问题有路程、时间和速度三个量,其关系式是路程=速度×时间,一般式以时间为等量关系。
(2)工程问题有工作效率、工作时间和工作总量三个量,其关系式是工作总量=工作效率×工作时间。
(3)增长率问题,其等量关系式是原量×(1+增长率)=增长后的量,原量×(1+减少率)=减少后的量。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1