一 : 证明：等腰三角形的两腰上的中线相等．
| 证明：等腰三角形的两腰上的中线相等． |
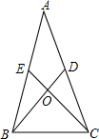 已知：等腰△ABC中，AB=AC，AD=DC，AE=EB， 求证：BD=CE． 证明：∵AB=AC，AD=DC，AE=EB， ∴DC=BE，∠DCB=∠EBC． ∵BC=CB， ∴△BDC≌△CEB（SAS）． ∴BD=CE． 即等腰三角形的两腰上的中线相等． |
考点：
考点名称：等腰三角形的性质，等腰三角形的判定定义：等腰三角形的性质：
1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。
3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)
等腰三角形的判定：
1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。
3.顶角的平分线，底边上的中分线，底边上的高的重合的三角形是等腰三角形。
二 : 数学等腰三角形一腰上的中线将三角形的周长分成21和12两个部分，
数学
等腰三角形一腰上的中线将三角形的周长分成21和12两个部分，求此三角形的腰长和底边长。
等腰三角形一腰上的中线将三角形的周长分成21和12两个部分，求此三角形的腰长和底边长。
解 设等腰三角形腰长为a,底为b.则
a+a/2=21;
b+a/2=12.
或
a+a/2=12;
b+a/2=21.
第一组方程解得:a=14,b=5.
第二组方程解得:a=8,b=17.不存在。
故三角形的腰长14,底边长5.
三 : 求三角形面积最大值一个等腰三角形腰上的中线长根号下3，求这三角形
求三角形面积最大值
一个等腰三角形腰上的中线长根号下3，求这三角形面积的最大值。
受二楼启发
设等腰三角形ABC两腰中线BE、CF交于G，则G为三角形ABC重心，
BG=CG=(2/3)√3
三角形ABC面积=3*三角形GBC面积=3*(1/2)*[(2/3)√3]^2*sinBGC≤2
这三角形面积的最大值2
四 : 如图1所示，等边△ABC中，AD是BC边上的中线，根据等腰三角形的“三线合一”特性，AD平分∠BAC
如图1所示，等边△ABC中，AD是BC边上的中线，根据等腰三角形的“三线合一”特性，AD平分∠BAC，且AD⊥BC，则有∠BAD=30°，BD=CD=
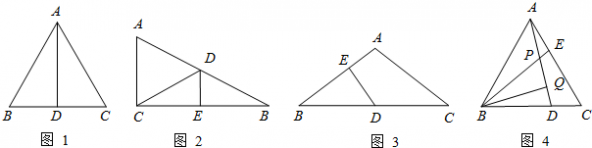 请根据从上面材料中所得到的信息解答下列问题： （1）△ABC中，若∠A：∠B：∠C=1：2：3，AB=a，则BC=______； （2）如图2所示，在△ABC中，∠ACB=90°，BC的垂直平分线交AB于点D，垂足为E，当BD=5cm，∠B=30°时，△ACD的周长=______． （3）如图3所示，在△ABC中，AB=AC，∠A=120°，D是BC的中点，DE⊥AB，垂足为E，那么BE：EA=______． （4）如图4所示，在等边△ABC中，D、E分别是BC、AC上的点，且∠CAD=∠ABE，AD、BE交于点P，作BQ⊥AD于Q，猜想PB与PQ的数量关系，并说明理由． |
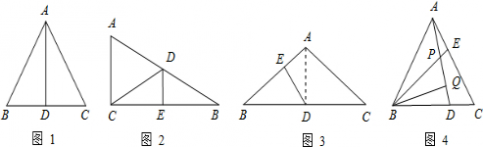 （1）∵∠A：∠B：∠C=1：2：3，且∠A+∠B+∠C=180°， ∴∠A=30，∠C=90°， ∴BC=
故填：
（2）如图2，∵DE是线段BC的垂直平分线，∠ACB=90°， ∴CD=BD，AD=BD． 又∵在△ABC中，∠ACB=90°，∠B=30°， ∴AC=
∴△ACD的周长=AC+AB=3BD=15cm． 故填：15cm； （3）如图3，连接AD． ∵在△ABC中，AB=AC，∠A=120°，D是BC的中点， ∴∠BAD=60°． 又∵DE⊥AB， ∴∠B=∠ADE=30°， ∴BE=
∴BE：EA=BD：AD=tan60°=
故填：
（4）BP=2PQ．理由如下： ∵△ABC为等边三角形． ∴AB=AC，∠BAC=∠ACB=60°， 在△BAE和△ACD中，
∴△BAE≌△ACD（SAS）， ∴∠ABE=∠CAD． ∵∠BPQ为△ABP外角， ∴∠BPQ=∠ABE+∠BAD． ∴∠BPQ=∠CAD+∠BAD=∠BAC=60° ∵BQ⊥AD， ∴∠PBQ=30°， ∴BP=2PQ． |
考点：
考点名称：直角三角形的性质及判定直角三角形定义：直角三角形性质：
直角三角形是一种特殊的三角形，它除了具有一般三角形的性质外，具有一些特殊的性质：
性质1:直角三角形两直角边a，b的平方和等于斜边c的平方。即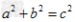
。如图，∠BAC=90°，则AB2+AC2=BC2（勾股定理)
性质2:在直角三角形中，两个锐角互余。如图，若∠BAC=90°，则∠B+∠C=90°
性质3：在直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。
性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
性质5: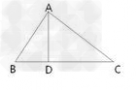
如图，Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，则有射影定理如下：
（1）（AD)2=BD·DC。
（2）（AB)2=BD·BC。
（3）（AC)2=CD·BC。
性质6:在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。
在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°。
性质7:如图，1/AB2+1/AC2=1/AD2
性质8:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
性质9：直角三角形直角上的角平分线与斜边的交点D 则 BD:DC=AB:AC
直角三角形的判定方法：
判定1：定义，有一个角为90°的三角形是直角三角形。
判定2：判定定理：以a、b、c为边的三角形是以c为斜边的直角三角形。如果三角形的三边a，b，c满足
，那么这个三角形就是直角三角形。（勾股定理的逆定理）。
判定3：若一个三角形30°内角所对的边是某一边的一半，则这个三角形是以这条长边为斜边的直角三角形。
判定4：两个锐角互为余角（两角相加等于90°）的三角形是直角三角形。
判定5：若两直线相交且它们的斜率之积互为负倒数，则两直线互相垂直。那么
判定6：若在一个三角形中一边上的中线等于其所在边的一半，那么这个三角形为直角三角形。
判定7：一个三角形30°角所对的边等于这个三角形斜边的一半，则这个三角形为直角三角形。（与判定3不同，此定理用于已知斜边的三角形。）
等腰三角形的性质：
1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。
3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)
等腰三角形的判定：
1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。
3.顶角的平分线，底边上的中分线，底边上的高的重合的三角形是等腰三角形。
性质：
①等边三角形是锐角三角形，等边三角形的内角都相等，且均为60°。
②等边三角形每条边上的中线、高线和所对角的平分线互相重合（三线合一）
③等边三角形是轴对称图形，它有三条对称轴，对称轴是每条边上的中线、高线 或对角的平分线所在的直线。
④等边三角形重心、内心、外心、垂心重合于一点，称为等边三角形的中心。（四心合一）
⑤等边三角形内任意一点到三边的距离之和为定值(等于其高)
判定方法：
①三边相等的三角形是等边三角形（定义）
②三个内角都相等（为60度）的三角形是等边三角形
③有一个角是60度的等腰三角形是等边三角形
④两个内角为60度的三角形是等边三角形
说明:可首先考虑判断三角形是等腰三角形。
等边三角形的性质与判定理解：
首先，明确等边三角形定义。三边相等的三角形叫做等边三角形，也称正三角形。
其次，明确等边三角形与等腰三角形的关系。等边三角形是特殊的等腰三角形，等腰三角形不一定是等边三角形。
等比三角形的尺规做法：
可以利用尺规作图的方式画出正三角形，其作法相当简单：先用尺画出一条任意长度的线段（这条线段的长度决定等边三角形的边长），再分别以线段二端点为圆心、线段为半径画圆，二圆汇交于二点，任选一点，和原来线段的两个端点画线段，则这二条线段和原来线段即构成一正三角形。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1