15+x已知15+x的参考答案设m= ,n=,那么m-n=2①,m2+n2=34②. 由①得,m=2+n③, 将③带入②得:n2+2n-15=0, 解得:n=-5(舍去)或n=3, 因此可得出,m=5,n=3(m≥0,n≥0). 所以 +2=n+2m=13.二 : 已知f(x)=x^2+c,且f[f(x)]=f(x^2+1)(1? 已知f(x)=x^ 2+c,且f[f(x)]=f(x^ 2+1) 已知f(x)=x^ 2+c,且f[f(x)]=f(x^ 2+1)
(1)设g(x)=f[f(x)],求g(x)的解析式
(2)设φ(x)=g(x)-λf(x),是否存在实数λ,使φ(x)在(-∞ ,-1)上是减,并且在(-1,0)上是增函数?
已知f(x)=x^ 2+c,且f[f(x)]=f(x^ 2+1) (1)设g(x)=f[f(x)],求g(x)的解析式 (2)设φ(x)=g(x)-λf(x),是否存在实数λ,使φ(x)在(-∞ ,-1)上是减函数,并且在(-1,0)上是增函数? (1)因为 f[f(x)]=f(x^ 2+1) 所以 (x^2+c)^2+c=(x^2+1)^2+c 展开整理得 (2c)x^2+c^2+c=2x^2+1+c 比较x的系数得 2c=2 c=1 所以 g(x)=(x^2+1)^2+1=x^4+2x^2+2 (2)φ(x)=x^4+2x^2+2-λ(x^2+1) =x^4+(2-λ)x^2+2-λ φ'(x)=4x^3+2(2-λ)x =x(4x^2+4-2λ) 所以 x=0 x=±√[(2λ-4)/4]是极值点 要 使φ(x)在(-∞ ,-1)上是减函数,并且在(-1,0)上是增函数,说明x=-1是极小点,令-√[(2λ-4)/4 ]=-1 得λ=4 所以存在λ=4 使φ(x)在(-∞ ,-1)上是减函数,并且在(-1,0)上是增函数。 三 : 已知f(x)是定义在[ 已知f(x)是定义在[-e,e]上的奇函数,当x∈(0,e)时,f(x)=ex+lnx,其中e是自然对数的底数.
(1)求f(x)的解析式;
(2)求f(x)的图象在点P(-1,f(-1))处的切线方程. |
题型:解答题难度:中档来源:不详
(1)设x∈[-e,0),则-x∈(0,e]
∴f(x)=-f(-x)=-[e-x+ln(-x)]
∵f(x)是定义在[-e,e]上的奇函数
∴f(0)=0
∴f(x)= | | -e-x+ln(-x),x∈[-e,0) | | 0,x=0 | | ex+lnx,x∈(0,e] |
| |
(2)f(-1)=-e,故P(-1,-e),
当x∈[-e,0),时f′(x)=ex-,f′(-1)=e+1
故过点P(-1,-e)的切线方程为y+e=(e+1)(x+1),即y=(e+1)x+1. |
考点: 考点名称:函数的奇偶性、周期性函数的奇偶性定义: 偶函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),则称函数f(x)为偶函数。
奇函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)是奇函数。
函数的周期性: (1)定义:若T为非零常数,对于定义域内的任一x,使f(x+T)=f(x)恒成立,则f(x)叫做周期函数,T叫做这个函数的一个周期。
周期函数定义域必是无界的。
(2)若T是周期,则k·T(k≠0,k∈Z)也是周期,所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期,如常函数f(x)=C。
奇函数与偶函数性质: (1)奇函数与偶函数的图像的对称性:奇函数的图像关于原点对称,偶函数的图像关于y轴对称。
(3)在公共定义域内,①两个奇函数的和是奇函数,两个奇函数的积是偶函数; ②两个偶函数的和、积是偶函数; ③一个奇函数,一个偶函数的积是奇函数。 注:定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件. 1、函数是奇函数或偶函数的前提定义域必须关于原点对称;定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件. 2、函数的周期性 令a,b均不为零,若:
(1)函数y=f(x)存在f(x)=f(x+a)==>函数最小正周期T=|a|
(2)函数y=f(x)存在f(a+x)=f(b+x)==>函数最小正周期T=|b-a|
(3)函数y=f(x)存在f(x)=-f(x+a)==>函数最小正周期T=|2a|
(4)函数y=f(x)存在f(x+a)=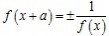 ==>函数最小正周期T=|2a| ==>函数最小正周期T=|2a|
(5)函数y=f(x)存在f(x+a)= ==>函数最小正周期T=|4a| ==>函数最小正周期T=|4a| 考点名称:函数解析式的求解及其常用方法函数解析式的常用求解方法: (1)待定系数法:(已知函数类型如:一次、二次函数、反比例函数等):若已知f(x)的结构时,可设出含参数的表达式,再根据已知条件,列方程或方程组,从而求出待定的参数,求得f(x)的表达式。待定系数法是一种重要的数学方法,它只适用于已知所求函数的类型求其解析式。
(2)换元法(注意新元的取值范围):已知f(g(x))的表达式,欲求f(x),我们常设t=g(x),从而求得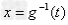 ,然后代入f(g(x))的表达式,从而得到f(t)的表达式,即为f(x)的表达式。 ,然后代入f(g(x))的表达式,从而得到f(t)的表达式,即为f(x)的表达式。
(3)配凑法(整体代换法):若已知f(g(x))的表达式,欲求f(x)的表达式,用换元法有困难时,(如g(x)不存在反函数)可把g(x)看成一个整体,把右边变为由g(x)组成的式子,再换元求出f(x)的式子。
(4)消元法(如自变量互为倒数、已知f(x)为奇函数且g(x)为偶函数等):若已知以函数为元的方程形式,若能设法构造另一个方程,组成方程组,再解这个方程组,求出函数元,称这个方法为消元法。
(5)赋值法(特殊值代入法):在求某些函数的表达式或求某些函数值时,有时把已知条件中的某些变量赋值,使问题简单明了,从而易于求出函数的表达式。 考点名称:函数的极值与导数的关系极值的定义: (1)极大值: 一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)<f(x0),就说f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0),x0是极大值点;
(2)极小值:一般地,设函数f(x)在x0附近有定义,如果对x0附近的所有的点,都有f(x)>f(x0),就说f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0),x0是极小值点。 极值的性质: (1)极值是一个局部概念,由定义知道,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小;
(2)函数的极值不是唯一的,即一个函数在某区间上或定义域内极大值或极小值可以不止一个;
(3)极大值与极小值之间无确定的大小关系,即一个函数的极大值未必大于极小值;
(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点,而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点。
判别f(x0)是极大、极小值的方法: 若x0满足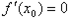 ,且在x0的两侧f(x)的导数异号,则x0是f(x)的极值点, ,且在x0的两侧f(x)的导数异号,则x0是f(x)的极值点,  是极值,并且如果 是极值,并且如果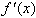 在x0两侧满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;如果 在x0两侧满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;如果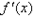 在x0两侧满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值。 在x0两侧满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值。 求函数f(x)的极值的步骤: (1)确定函数的定义区间,求导数f′(x);
(2)求方程f′(x)=0的根;
(3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格,检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号即都为正或都为负,则f(x)在这个根处无极值。 对函数极值概念的理解: 极值是一个新的概念,它是研究函数在某一很小区域时给出的一个概念,在理解极值概念时要注意以下几点:
①按定义,极值点x0是区间[a,b]内部的点,不会是端点a,b(因为在端点不可导).如图
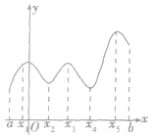
②极值是一个局部性概念,只要在一个小领域内成立即可.要注意极值必须在区间内的连续点取得.一个函数在定义域内可以有许多个极小值和极大值,在某一点的极小值也可能大于另一个点的极大值,也就是说极大值与极小值没有必然的大小关系,即极大值不一定比极小值大,极小值不一定比极大值小,如图.
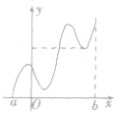
③若fx)在(a,b)内有极值,那么f(x)在(a,b)内绝不是单调函数,即在区间上单调的函数没有极值.
④若函数f(x)在[a,b]上有极值且连续,则它的极值点的分布是有规律的,相邻两个极大值点之间必有一个极小值点,同样相邻两个极小值点之间必有一个极大值点,一般地,当函数f(x)在[a,b]上连续且有有
限个极值点时,函数f(x)在[a,b]内的极大值点、极小值点是交替出现的,
⑤可导函数的极值点必须是导数为0的点,但导数为0的点不一定是极值点,不可导的点也可能是极值点,也可能不是极值点,
本文标题:已知f(x)-已知15+x
本文地址: http://www.61k.com/1072357.html |