一 : 正方形里画一个最大的圆,有几条对称轴？

正方形里画一个最大的圆,有几条对称轴?

正方形里画一个最大的圆,有几条对称轴？的参考答案

4条

2条对边中点连线所在直线

2条对角线所在直线

hjjhxrz 来自 数学辅导团 团队

二 : 四维超正方体：四维超正方体-四维超正方体，四维超正方体-对称群构造

四维超正方体是一种四维的超正方体（英语：hypercube）。在几何学中，四维超正方体是立方体的四维类比，有8个立方体胞。四维超正方体之于立方体，就如立方体之于正方形。

超正方体_四维超正方体 -四维超正方体

（www.61k.com]（英语：tesseract）或正八胞体，是1种四维的超正方体（英语：hypercube）。在几何学中，四维超正方体是立方体的四维类比，有八个立方体胞。四维超正方体之于立方体，就如立方体之于正方形。

在四维欧几里得空间的标准四维方体是点(±1,±1,±1,±1)的凸包。它包含了点：

四维方体由8个超平面(xi=±1)包围。两两非平行超平面相交，共形成四维方体的二十四个正方形面。每条棱有三个立方体和三个正方形相交。在每一顶点有四个立方体、六个正方形和4条棱相交。四维方体共有八个立方体、二十四个正方形、32条棱和十六个顶点。
四维方体的每一顶点与4条棱相邻，所以四维方体的顶点形是正四面体。所以四维方体的施莱夫利符号是{4,3,3}。其对偶多胞体是正十六胞体，施莱夫利符号是{3,3,4}。

超正方体_四维超正方体 -对称群构造

作为1个超方形，超立方体可被识别为不同对称群的多胞体：首先，它是四维的超方形——1个凸正多胞体——四维超立方体，对应施莱夫利符号{4,3,3}，Coxeter-Dynkin符号为，具有考斯特BC4对称群（即超方形—正轴形对称群）构造，阶为384。同时，它也可被看作是立方体的四维棱柱，对应施莱夫利符号{4,3}×{}，Coxeter-Dynkin符号，这个对称群的阶只有96。并且，它还是四维以上高维才有的2个二维以上多胞形的欧拉乘积——复棱柱的1个，即4,4复棱柱，是2个正方形的乘积，对应施莱夫利符号{4}×{4}，Coxeter-Dynkin符号为，群阶64。它还是正四棱柱棱柱{4}×{}×{}，，群阶32。它还是线段棱柱棱柱棱柱{}×{}×{}×{}，，群阶16。

超正方体_四维超正方体 -投射

四维方体不易想象，但可以投射至3维或2维空间。在2维平面的投射，把顶点位置调整后，可以了解更多。如此获得的图像，不再反映四维方体空间构造，而是反映顶点间的联系。以下给出一些例子。

第一幅图显示四维方体本质上从结合两个立方体，连结对应顶点得来。第二幅图反映出四维方体每条边等长，也可以看出立方体如何互相连结。第三幅图按著每一顶点由最底一顶点出发沿着棱走的长度排列。

四维立方
四维立方
四维立方

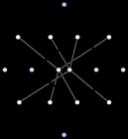
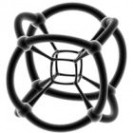
超正方体_四维超正方体 -可视化

可视化四维立方
可视化四维立方
可视化思维立方
四维立方展开图

三 : 正方形有几条对称轴？[]A．1B．2C．4D．无数

正方形有几条对称轴？

[ ]

A．1 B．2 C．4 D．无数

题型：单选题难度：中档来源：同步题

C

考点：

考点名称：轴对称，轴对称图形如果一个图形沿着一条直线对折，直线两边的图形能够完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴。
学过的图形中，线段、角、等腰三角形、等边三角形、长方形、正方形、等腰梯形、圆形、扇形都是轴对称图形，各自有不同数目的对称轴。

四 : 试确定如图所示的正多边形的对称轴的条数，一般地，一个正n边形有多少条对称轴？正多边形边数345678

试确定如图所示的正多边形的对称轴的条数，一般地，一个正n边形有多少条对称轴？ 正多边形边数 3 4 5 6 7 8 对称轴条数 根据上表，可以猜想得到：一个正n边形有对称轴______条．

题型：解答题难度：中档来源：不详

如图所示： 正多边形边数 3 4 5 6 7 8 对称轴条数 3 4 5 6 7 8 根据上表，可以猜想得到：一个正n边形有对称轴n条．

考点：

考点名称：探索规律探索规律的题目，通常按照一定的顺序给出一系列量，要求我们根据这些已知的量找出一般规律。揭示的规律，常常包含着事物的序列号。所以，把变量和序列号放在一起加以比较，就比较容易发现其中的奥秘。
掌握探究的一般方法是解决此类问题的关键。
（1）掌握探究规律的方法，可以通过具体到抽象、特殊到一般的方法，有时通过类比、联想，还要充分利用已知条件或图形特征进行透彻分析，从中找出隐含的规律；
（2）恰当合理的联想、猜想，从简单的、局部的特殊情况到一般情况是基本思路，经过归纳、提炼、加工，寻找出一般性规律，从而求解问题。

探索规律题题型和解题思路:
1.探索条件型:结论明确,需要探索发现使结论成立的条件的题目;
探索条件型往往是针对条件不充分、有变化或条件的发散性等情况，解答时要注意全面性，类似于讨论；解题应从结论着手，逆推其条件，或从反面论证，解题过程类似于分析法。

2.探索结论型:给定条件,但无明确的结论或结论不唯一,而要探索发现与之相应的结论的题目;
探索结论型题的特点是结论有多种可能，即它的结论是发散的、稳定的、隐蔽的和存在的；
探索结论型题的一般解题思路是：
（1）从特殊情形入手，发现一般性的结论；
（2）在一般的情况下，证明猜想的正确性；
（3）也可以通过图形操作验证结论的正确性或转化为几个熟悉的容易解决的问题逐个解决。
3.探索规律型:在一定的条件状态下,需探索发现有关数学对象所具有的规律性或不变性的题目；
图形运动题的关键是抓住图形的本质特征，并仿照原题进行证明。在探索递推时，往往从少到多，从简单到复杂，要通过比较和分析，找出每次变化过程中都具有规律性的东西和不易看清的图形变化部分。

4.探索存在型:在一定的条件下,需探索发现某种数学关系是否存在的题目.而且探索题往往也是分类讨论型的习题,无论从解题的思路还是书写的格式都应该让学生明了基本的规范,这也是数学学习能力要求。
探索存在型题的结论只有两种可能：存在或不存在；
存在型问题的解题步骤是：
①假设存在；
②推理得出结论（若得出矛盾，则结论不存在；若不得出矛盾，则结论存在）。
解答探索题型，必须在缜密审题的基础上，利用学具，按照要求在动态的过程中，通过归纳、想象、猜想，进行规律的探索，提出观点与看法，利用旧知识的迁移类比发现接替方法，或从特殊、简单的情况入手，寻找规律，找到接替方法；解答时要注意方程思想、函数思想、转化思想、分类讨论思想、数形结合思想在解题中的应用；因此其成果具有独创性、新颖性，其思维必须严格结合给定条件结论，培养了学生的发散思维，这也是数学综合应用的能力要求。

五 : 正方形有几条对称轴？[]A．1B．2C．3D．4

正方形有几条对称轴？

[ ]

A．1 B．2 C．3 D．4

题型：单选题难度：偏易来源：陕西省同步题

D

考点：

考点名称：轴对称，轴对称图形如果一个图形沿着一条直线对折，直线两边的图形能够完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴。
学过的图形中，线段、角、等腰三角形、等边三角形、长方形、正方形、等腰梯形、圆形、扇形都是轴对称图形，各自有不同数目的对称轴。 本文标题：正方形有几条对称轴-正方形里画一个最大的圆,有几条对称轴？
本文地址： http://www.61k.com/1068897.html