一 : 如图，在直角梯形ABCD中，DC∥AB，∠A=90°，AB=28cm，DC=24cm，AD=4cm，

如图，在直角梯形ABCD中，DC∥AB，∠A=90°，AB=28cm，DC=24cm，AD=4cm，点M从点D出发，以1cm/s的速度向点C运动，点N从点B同时出发，以2cm/s的速度向点A运动，当其中一个动点到达端点停止运动时，另一个动点也随之停止运动．则四边形ADMN的面积y（cm2）与两动点运动的时间t（s）的函数图象大致是（　　） A． B． C． D．

题型：单选题难度：偏易来源：不详

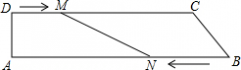因为在直角梯形ABCD中，DC∥AB，∠A=90°， 所以四边形ANMD也是直角梯形，因此它的面积为 1 2 （DM+AN）×AD，因为DM=t，AN=28-2t，AD=4； 所以四边形AMND的面积y= 1 2 （t+28-2t）×4=-2t+56． 因为当其中一个动点到达端点停止运动时，另一个动点也随之停止运动； 所以当N点到达A点时，2t=28，t=14； 所以自变量t的取值范围是0＜t＜14． 故选D．

考点：

考点名称：函数的图像

函数图象的概念：
对于一个函数，如果把自变量x和函数y的每对对应值分别作为点的横坐标与纵坐标，在坐标平面内描出相应的点，这些点所组成的图形，就是这个函数的图象．

由函数解析式画其图象的一般步骤：
①列表：列表给出自变量与函数的一些对应值；
②描点：以表中每对对应值为坐标，在坐标平面内描出相应的点；
③连线：按照自变量由小到大的顺序，把所描各点用平滑的曲线连接起来．

利用函数的图象解决实际问题，其关键是正确识别横轴和纵轴的意义，正确理解函数图象的性质，正确地识图、用图．

函数图象上的点的坐标与其解析式之间的关系：
①由图象的定义可知图象上任意一点P（x，y）中的x，y是解析式方程的一个解，反之，以解析式方程的任意一个解为坐标的点一定在函数图象上；
②通常判定点是否在函数图象上的方法是：将这个点的坐标代入函数解析式，如果满足函数解析式，这个点就在函数的图象上，如果不满足函数解析式，这个点就不在其函数的图象上，反之亦然；
③两个函数图像的交点就是饿两个函数解析式所组成的方程组的解。

二 : 关于二面角，救救我，明天要交在正方体ABCD-A1B1C1D1中

关于二面角，救救我，明天要交

在正方体AB-A1B1C1D1中，E1为A1D1的中点
1.求二面角E1-AB-C的大小
2.求二面角C1-B1D1-A的大小

---

取AD的中点E 连接E和E1，

因为此两点均为中点

所以EE1垂直于平面ABC

又因为AD垂直于AB

根据三垂线定理得

角E1AD即为所求

而AD=0.5E1E

所以所求角度为

arctan2=63.4°

三 : 解直角三角形~~如图，甲船在港口P的北偏西60°方向，距港口80

解直角三角形~~

如图，甲船在P的北偏西60°方向，距港口80海里的A处，沿AP方向以12海里/时的速度驶向港口P。乙船从港口P出发，沿北偏东45°方向匀速驶离港口P，现两船同时出发，2小时后乙船载甲船的正东方向。求乙船的航行速度。（精确到0.1海里/时，参考数据√2≈1.41，√3≈1.73）

---

以P点为原点，东西方向为x轴。

经过2小时，甲船到达B点，乙船到达C点。

因为这时乙船在甲船的正东方向，所以B点到x轴的距离=C点到x轴的距离。

AB = 12 *2 = 24海里

PB = 80 - 24 = 56海里

B点到x轴的距离 = PB * cos60°= 28海里

设乙船的航速为x海里/时，PC = 2x

C点到x轴的距离 = PC * cos45°= x*√2 = 1.41x

1.41x = 28

x ≈ 19.9

乙船的航行速度约为19.9海里/时

四 : 如图1，在直角梯形ABCD中，∠ADC=90°，CD∥AB，AB=4，AD=CD=2．将△ADC沿A

如图1，在直角梯形ABCD中，∠ADC=90°，CD∥AB，AB=4，AD=CD=2．将△ADC沿AC折起，使平面ADC⊥平面ABC，得到几何体D-ABC，如图2所示． （Ⅰ）求证：BC⊥平面ACD； （Ⅱ）求几何体D-ABC的体积．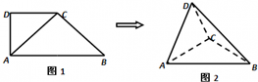

题型：解答题难度：中档来源：哈尔滨模拟

（Ⅰ） 【解法一】：在图1中，由题意知，AC=BC=2 2 ，∴AC2+BC2=AB2，∴AC⊥BC 取AC中点O，连接DO，则DO⊥AC，又平面ADC⊥平面ABC， 且平面ADC∩平面ABC=AC，DO?平面ACD，从而OD⊥平面ABC， ∴OD⊥BC 又AC⊥BC，AC∩OD=O， ∴BC⊥平面ACD 【解法二】：在图1中，由题意，得AC=BC=2 2 ，∴AC2+BC2=AB2，∴AC⊥BC ∵平面ADC⊥平面ABC，平面ADC∩平面ABC=AC，BC?面ABC，∴BC⊥平面ACD （Ⅱ）由（Ⅰ）知，BC为三棱锥B-ACD的高，且BC=2 2 ，S△ACD= 1 2 ×2×2=2， 所以三棱锥B-ACD的体积为：VB-ACD= 1 3 Sh= 1 3 ×2×2 2 = 4 2 3 ， 由等积性知几何体D-ABC的体积为： 4 2 3 ．

考点：

考点名称：柱体、椎体、台体的表面积与体积

侧面积和全面积的定义：

(1)侧面积的定义：把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开，所得到的展开图的面积，就是空间几何体的侧面积．
(2)全面积的定义：空间几何体的侧面积与底面积的和叫做空间几何体的全面积，

柱体、锥体、台体的表面积公式（c为底面周长，h为高，h′为斜高，l为母线）

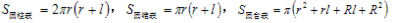
柱体、锥体、台体的体积公式：

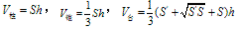
多面体的侧面积与体积：

多面体	图像	侧面积	体积
棱柱		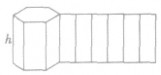直棱柱的侧面展开图是矩形
棱锥		正棱柱的侧面展开图是一些全等的等腰三角形，
棱台		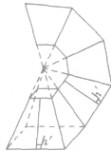正棱台的侧面展开图是一些全等的等腰梯形，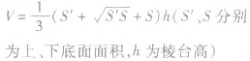

旋转体的侧面积和体积：

旋转体	图形	侧面积与全面积	体积
圆柱		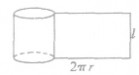圆柱的侧面展开图的矩形：
圆锥		圆锥的侧面展开图是扇形：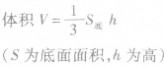
圆台		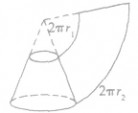圆台的侧面展开图是扇环：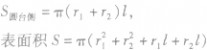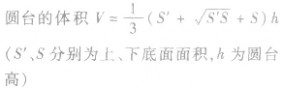
球

考点名称：直线与平面垂直的判定与性质

线面垂直的定义：

如果一条直线l和一个平面α内的任何一条直线垂直，就说这条直线l和这个平面α互相垂直，记作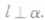直线l叫做平面α的垂线，平面α叫做直线l的垂面。直线与平面垂直时，它们唯一的公共点P叫做垂足。

线面垂直的画法：

画线面垂直时，通常把直线画成与表示平面的平行四边形的一边垂直，如图所示：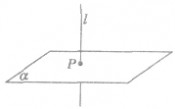

线面垂直的判定定理：

如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直这个平面。（线线垂直线面垂直）

符号表示：

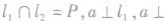
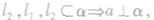如图所示，

线面垂直的性质定理：

如果两条直线同垂直于一个平面，那么这两条直线平行。
（线面垂直线线平行）

线面垂直的判定定理的理解：

(1)判定定理的条件中，“平面内的两条相交直线”是关键性语句，一定要记准．
(2)如果一条直线垂直于平面内的两条直线，那么这条直线垂直于这个平面，这个结论是错误的．
(3)如果一条直线垂直于平面内的无数条直线，那么这条直线垂直于这个平面，这个结论也错误，因为这无数条直线可能平行.

证明线面垂直的方法：

(1)线面垂直的定义拓展了线线垂直的范围，线垂直于面，线就垂直于面内所有直线，这也是线面垂直的必备条件，利用这个条件可将线线垂直与线面垂直互相转化，这样就完成了空间问题与平面问题的转化．
(2)证线面垂直的方法①利用定义：若一直线垂直于平面内任一直线，则这条直线垂直于该平面．②利用线面垂直的判定定理：证一直线与一平面内的两条相交直线都垂直，③利用线面垂直的性质：两平行线中的一条垂直于平面，则另一条也垂直于这个平面，④用面面垂直的性质定理：两平面垂直，在一个平面内垂直于交线的直线必垂直于另一个平面．⑤用面面平行的性质定理：一直线垂直于两平行平面中的一个，那么它必定垂直于另一个平面．⑥用面面垂直的性质：两相交平面同时垂直于第三个平面，那么两平面的交线垂直于第三个平面．⑦利用向量证明．

本文标题：如图在直角梯形abcd中-如图，在直角梯形ABCD中，DC∥AB，∠A=90°，AB=28cm，DC=24cm，AD=4cm，
本文地址： http://www.61k.com/1060317.html