一 : 直线加速器:直线加速器-历史,直线加速器-原理
61阅读/ www.61k.net
直线加速器通常是指利用高频电磁场进行加速,同时被加速粒子的运动轨迹为直线的加速器。高频直线加速器(high-frequency linear accelerator)简称直线加速器,是指用沿直线轨道分布的高频电场加速带电粒子的装置。按被加速粒子的种类,可分为电子直线加速器、质子直线加速器、重离子直线加速器和超导直线加速器等。
直线加速器_直线加速器 -历史
直线加速器的雏形概念最早是由英国科学家G.Ising在1924年提出,1924年他在一篇名为《产生高压极隧射线方法原理》的文章中提出了1个直线加速器的设计图样。根据G.Ising的文章,直线加速器由1个直的真空管道和一系列的带孔的金属漂移管组成。粒子的加速是通过相邻的漂移管之间的脉冲电场完成的,电场和粒子的同步是由电压源和相应的漂移管之间的传输线长度的时间延迟来实现。同时他在文章中写道:“现在来深入讨论实现这一想法的细节问题和可能遇到的困难为时尚早,我希望不久能做1个实验。”这个建议在当时由于电磁技术的水平所限制的确难以实现。但是这个概念相当重要,对直线加速器的发展产生了里程碑式的影响。到了 1928年,直线加速器的概念正式被德国科学家RolfWideroe提出,他完成了世界上第一台直线加速器。R.Wideroe在《产生高电压的新原理》一文中描述了这台加速器的原理,同G.Ising的理念不同,加速器的漂移管是交替的接高频电源和接地。移管的长度随着粒子速度的增加而变长,保证粒子每次可以在正确的时间到达间隙从而被加速。在该加速器中,束流首先形成束团,然后进行高效率的加速。束流在加速时间内处于加速间隙感受加速电场,当电场反向的时候,束团处于漂移管中,这时漂移管屏蔽了减速电场,从而使整个过程是1个加速过程。

1928年E.维德罗提出加速原理。早期利用频率不太高的交变电场加速带电粒子,1946年后利
用射频微波来加速带电粒子。在柱形金属空管(波导)内输入微波,可激励各种模式的电磁波,其中1种模式沿轴线方向的电场有较大分量,可用来加速带电粒子。为了使沿轴线运行的带电粒子始终处于加速状态,要求电磁波在波导中的相速降低到与被加速粒子运动同步,这可以通过在波导中按一定间隔安置带圆孔的膜片或漂移管来实现。电子的质量很小,仅几兆电子伏。
中国科学院高能物理研究所35MeV质子直线加速器的加速腔的能量时,电子的速度已接近光速,带圆孔的膜片装置适用于加速电子;质子或离子的质量较大,其速度较低,常采用带漂移管的装置。1966年建成的美国斯坦福电子直线加速器管长3050米,电子能量高达22吉电子伏,脉冲电子流强约80毫安,平均流强为48微安。
直线加速器_直线加速器 -原理

加速器是由三根用绝缘材料制成的高柱和在它们中间的加速器管组成。加速器靠真空泵
保持真空。外表流线型,不仅为了美观,而且为了防止从任何棱角或突出部分形成意外的放电。
在加速器管中有金属圈,它们同高压发生器相连的方式能使一系列金属圈的负压由底部向顶端逐渐升高。生产质子的离子源安装在加速器管的上端。带正电的质子由于受到带负电的金属圈的吸引而顺管射下——由于下面金属圈的负电压不断增大,质子的速度也不断增加。在加速器管的地端的地板下面,有一间装有接收器的小室,质子能够在这里同物质碰撞,在此过程中,轰击能够引起原子核的蜕变。
直线加速器_直线加速器 -主要特点
束流的注入和引出很方便,束流强、传输效率高、束品质较好,可由前至后分段设计、制造和调试。由于加速器不存在偏转束的同步辐射限制,可将电子束加速到很高能量,是下一代超高能对撞机的唯一候选者(见对撞机)。为使加速器有适当的长度,轴上加速电场强度一般在5—25兆伏/米,需要很大的微波功率源,因此单位束流功率所需造价和运行费用较高。现今提出的超导加速器可有效地降低运行费用。
直线加速器_直线加速器 -行波与驻波加速
荷电粒子在高频直线加速器中是用高频(或微波)电场的轴向分量进行加速。按采用的加速波分类,有行波与驻波2类。前者用圆柱波导作为加速结构,在其内沿轴周期性地设置圆盘负载,使波导中传播的相速小于或等于光速,以利同步地加速粒子,其加速场的模式为类-TM,它在近轴区提供最大的轴向电场分量。后者采用圆柱形谐振腔,也沿轴周期性地设置电极(或称漂移管)负载,以提高有效加速电场强度,其加速场的模式为类-TM,同样在近轴区提供最大的轴向电场分量。衡量加速结构性能的主要参数有2类:一是与加速效率有关的参量,特别是有效分路阻抗。它表示给定高频功率损耗,结构能建立多高的加速电场。分路阻抗的高低决定于选用的频率、结构的几何尺寸与形状及相邻加速单元间高频相位的变化量(工作模式)。通常频率越高,结构尺寸越小,分路阻抗和加速效率越高。二是加速结构的稳定性,它表征由于结构的误差和邻近非加速模式对束流的影响。对驻波加速结构,实现稳定性的主要途径是采用所谓的双周期结构,即除了由负载形成的周期性加速单元外,还引进周期性的耦合单元,调节耦合单元的位置和尺寸,便可提高结构的抗干扰性。
直线加速器_直线加速器 -分类
按被加速粒子的种类,可分为电子、质子和重离子直线加速器。
电子直线加速器
可采用行波或驻波加速粒子。当采用行波加速时,可使结构设计成等阻抗或等梯度型。等阻抗型是1种均匀的加速结构,即结构的各尺寸沿轴不变,便于设计和制造,缺点是微波功率在结构中的损耗不均匀,对较长的直线加速器来说,沿轴的结构温控较不容易。等梯度型加速结构避免了这个缺点,代价是沿轴的结构尺寸有慢变化,使设计和制造较复杂些。
质子直线加速器
质子的静止质量是电子的1,800多倍,在其很长的加速范围内,速度远小于或小于光速,因而采用驻波加速结构,以获得较高的有效分路阻抗和加速效率。质子的动能由1兆电子伏到1,000兆电子伏,其速度由光速的4.6%到87.5%。为使结构在不同能区均有较高的加速效率,需采用不同的结构。如:①质子的动能由小于1兆伏加速到几兆伏,可采用高频四极型加速结构(Radio Frequency Quadrupole,RFQ)。在一圆柱腔的中心部位,方位角对称地设置4个轴向高频电极,在它们所围的近轴区,产生四极聚焦电场,以径向聚焦束流;沿轴可周期性地调变每个电极的径向尺寸,以得到在轴向群聚和加速束流的轴向电场。它兼具聚束、聚焦和加速几种作用,是20世纪70年代兴起的加速结构,选用频率为200—400兆赫。②质子动能要由几兆电子伏加速到150兆电子伏左右,可采用漂移管型结构(又称阿尔瓦雷茨结构),是20世纪40年代末由L.阿尔瓦雷茨首先提出和建造的。在圆柱形腔内,沿轴周期性地设置长度随能量渐增的电极。当高频电场处在正半周时,质子束团在电极间被加速;当处在负半周时,质子束团躲在电极内不受负半周减速场的影响而漂移前进,故又称电极为漂移管。在漂移管内安放四极磁铁,可径向聚焦束流,选用的频率为200—400兆赫。③当质子动能要由150兆电子伏加速到更高能量,通常采用耦合腔加速结构。在该能区内对质子束的径向聚焦已较容易,可将四极磁铁移到加速腔外,使频率提高到800—1,300兆赫,以提高加速效率。这种结构也可用于加速电子,工作频率通常为1,300—3,000兆赫。
重离子直线加速器
较接近于质子直线加速器,只是在同样动能下,粒子运动速度更低,因而工作频率也更低,一般在27—150兆赫左右。早期的这类加速器,采用维德罗加速结构。现代的这类加速器按能区可采用高频四极型或阿瓦莱兹型。现今发展的重离子加速结构,如柱形和平面螺旋线结构、分离环谐振腔结构等,它们的特点是径向尺寸较小、公差要求较松、可做成许多短腔组合成整台加速器,既便于采用超导技术,又利于展宽重离子的范围和能量连续可变的需求。
超导直线加速器
利用超导材料做成的结构,其功耗几乎可略去不计,因而可用较小微波功率建立较高的加速电场。这类加速腔大多采用内表面涂有氧化保护层的纯铌材料制成,置于液氮和液氦逐级冷却的低温容器中,可冷却至4.2K或更低。加速电场可达几兆伏/米至20兆伏/米以上。将超导腔用于高能直线加速器,优势更显着。如用于强流质子直线加速器的高能段(约150—1,000兆电子伏),由于功耗可略去不计,可选用束通道孔径较大的结构,可有效避免高能强流束沿途损失造成严重的放射性污染。此外,还有利于提高加速场强,减小设备规模和运行费用等。提议中的超导正负电子直线对撞机(TESLA),选用比其他同类对撞机方案(5,700—11,400兆赫)低得多的频率(1,300兆赫)和较大的束孔径,除仍有较高的加速电场(约25兆伏/米)外,束流在腔壁上感生的尾场相对很小,较易确保束流的高品质(发射度小、能散小等)。
直线加速器是各类加速器中被最广泛应用的加速器类型(见粒子加速器)。
直线加速器_直线加速器 -医学应用
产品用途
双光子医用直线加速器是用于癌症放射治疗的大型医疗设备,它通过产生X射线和电子线,对病人体内的肿瘤进行直接照射,从而达到消除或减小肿瘤的目的。
产品特点
①能量分档多,能量范围宽。
设计有完善的多级安全联锁,确保人员和设备的安全。
②全数字化的设计,整机采用计算机控制,操作软件采用图形界面,操作更简便。自动频率控制(AFC)、自动束流控制(AIC)、剂量监视和自动均整度控制(ADC)等控制系统全部采用微处理器控制,剂量更稳定。
③独立双通道的电离室设计,确保剂量测量的准确性。偏转系统采用滑雪式消色散结构,可获得更好的束流分布。
④加速管采用行波反馈系统,具有能量范围宽、能量稳定性高、束流能谱好,快速瞬态反应等的特点。配合大功率的微波反馈系统,最高微波能量高达6MW。
⑤限束装置的上下光阑可分别独立运动,适应不同治疗种类的需要。中心精度高。可配外置的X刀、多叶光栅等适形治疗系统。具有远程故障诊断功能,可通过互联网协助用户进行维护,维修更简便。
二 : 直线加速器
1. 假设宇宙线中的质子进入大气层时的能量为1焦耳,换算成TeV是多少,并计算质子的
速度和?。
1[J]?6.25?1018[eV]?6.25?106[TeV] ?191.6?10[C]
??E19 ??6.66?10?19E0938.272?1.6?10
???1
?2?1
v??c?c
2. 推导dEdP和之间的关系。 EP
?? v
c
??1
??2
E??m0c2
P??m0v
d??v3vdv??dv 22c2cv?2c1
2dEd?(m0c2)d?2vdv22dv ???????22E?m0c?cvv
dPd?(mv)??mdv?P?m0v
?3m0?2dv??m0dv??m0v
??2?2?1
dv
v
dEdP??2 EP??2
??dvv
3. 地磁场约为1Gs,计算质子在多大速度时受到的磁场力与所受到的重力相当,并计算相
应的动能。
evB?mpg
1.67?10?27?9.8v???0.001[m/s] ?19eB1.6?10?0.0001
1Ek?mpv2?8?10?34[J]?5?10?15[eV] 2
4. CSNS打靶的质子束流能量为1.6 GeV,平均流强为62.5 ?A,计算束流的平均功率。 mpgP?I?Ek?e?I?Ek?62.5?10?6?1.6?109?100[kW] e
5. 加速器中为什么使用TM波用于加速,而不是TE波,是如何使相速小于光速的? TM波有纵向的电场分量可用于加速带电粒子,而TE波没有纵向电场分量。在圆波导中加入周期性的盘荷负载后,产生的空间谐波分量可提供小于或等于光速的相速。
6. BEPC直线加速器的行波加速结构的工作频率为2856 MHz,计算加速场的波长。
c3?108[m/s]????0.105[m] 6f2856?10[Hz]
7. 如果圆波导的直径2b从8.4 cm变化到8.2 cm,计算截止频率。
?cr1c13?108[m/s]fcr???2.405???2.405??2.8[GHz] 2?2?b2?4.1[cm]
8. 高频波长为λ= 12 cm的直线加速器,分别计算其?/2模、0模、2?/3模、?模的单元
(Cell)长度。
?/2模:Lc??
???2?/???2??12[cm]?3[cm] 4
0模:Lc??
2?/2??12[cm]?12[cm] 1
?12[cm]?4[cm] 32?/3模:Lc??
?2?2?/???3?
?模:Lc??12[cm]??6[cm] 2?/?2
9. 设一行波电子直线加速器,为等梯度加速结构,结构的主要参数为: 工作频率f0?2998MHz,工作模式2?/3,每加速节长30?0,平均分路阻抗Zs?56M?/m,每节衰减常数?0?0.55;每节加速结构各有一功率源,它向加速结构输入的最大脉冲功率为30MW。
请回答下列问题:
(1) 加速结构的最大加速梯度是多少?
(2) 在每节加速结构的尾部的剩余输出功率是多少?
(3) 每节的最大能量增益是多少?
(4) 若将束流能量由20MeV加速到600MeV,需几节加速结构? 共有多少个加速单元?
(2)每节加速结构的尾部的剩余输出功率:
Pout?P0e?2?0
?30MW?e?2?0.55
?10MW
(1)单位长度的功率损失: P?P30MW?10MW?dP?????6.67MW/m ????dzL3m??
加速结构的最大加速梯度:
Ea??Zs
dP?56M?/m?6.67MW/m?19.33MV/m dz
(3)每节加速结构的长度为: c2.9979?108
L?30?0?30??30??3m 6f2998?10
每节加速结构的能量增益:
?W?eEaLcos00?e?19.33MV/m?3m?58MeV
(4)将束流能量由20MeV加速到600MeV,所需加速结构数量:
N?600?20?10 58
每节加速结构的加速单元个数:30?3?90
所需加速单元总个数:90?10?900
10. 加速结构的分路阻抗由什么决定?等阻抗和等梯度加速结构有什么区别?
加速结构的分路阻抗决定于结构的形状、尺寸、材料和工作模式。
等阻抗加速结构每个单元的几何参数都一样,Q、vg、Zs和?0都相同,高频功率和电场沿传播方向指数衰减。
等梯度加速结构通过调整各加速腔的横向几何尺寸a和b,使得加速电场始终保持恒定。与等阻抗加速结构相比,在同样的能量增益的情况下,等梯度加速结构的能量损失均匀。
10. 设一质子直线加速器,工作频率为200 MHz, 渡越时间因子 T?0.85,同步相位为
?s??30o,初始速度 ??
v?0.15,束流相对于同步粒子的初始能量范围为 c?0.45MeV。 试求:为在纵向俘获该束流,要求加速器入口的加速电场至少多高?
33?2?2eET????m0c?(?cos??sin?)sss?2??m0c?1/2答: 纵向稳定区的最大能量范围?Wmax
不小于束流的能量范围, ,应
?2?E0(MV/m)?0.85?(0.15)3?(1.011)3?1.5m?0.45MeV?938MeV?(?0.52?0.866?(?0.5))?3.14?938MeV??1/2
0.45MeV?938MeV1.41?10?7E0
E0?
??1/2 0.451,E0?1.64MV/m ?7938.4?10
11. CSNS注入H-束流的能量为80 MeV,引出质子束流的能量为1.6 GeV,计算这两种情况
下束流的磁刚度。
??EE?E ?E0E0
???1
?2
mv?mc2v? B????(E?E)0k2qqcc
c? 299792458[m/s]
(1) 注入H-束流:
H-的静止能量约为1个质子和2个电子静止能量的总和:
E0?938.272[MeV]?2?0.511[MeV]?938.783[MeV]
??1.08517
??0.388344
B??(E0?Ek)?
c?1.32037[T?m] (1.31946 [T?m])
(2)引出质子束流:
E0?938.272[MeV]
??2.70526
??0.929171
B??(E0?Ek)
12. CSNS高能输运线的工作能量为1.6 GeV,四极磁铁内径为?180 mm,磁铁极面场强最大为7000 Gs,求四极磁铁强度K的最大值。 ?c?7.86707[T?m] (1.86163 [T?m])
K?1?By1?B ?B??xB??y
Kmax?
?1??By????B???x??max1gmaxB?
1Bmax ?B?r
10.7??7.86710.180/2
?0.9886[m?2]
13. 推导等梯度行波加速管在高能情况下(v=c)的横向传输矩阵。 高能情况下?E
E??2?P
P??P
P,
设加速管长度为L,束流在进入加速段前动量为P0,水平方向动量分量为P?x0,则
x'(0)?P?x0。 P0
在经过加速管后束流动量增加量为?P,则
PPx'(0)Px'(s)??? P0?1?1?LP0?LP0?L
x'(L)?x'(0) 1?P0
Lx(L)?x(0)??x'(s)ds0
?x(0)??L
0x'(0)ds1?P0?L
?x(0)?L?x'(0)?Pln(1?)?PP0
P0
表示成矩阵形式:
??1??x(L)????x'(L)???????0???
传输矩阵为: L?P?ln(1?)??PP0???x(0)?P0???x'(0)?? 1????P?1??P0?
??1??R???0
???L?P?ln(1?)?P0?P0?? 1??1??P0?
考虑到加速管的加速相位,设能量增益为?E,则
E0?Ecos???ln(1?)??1L?Ecos?E0? R??E??0??E0??Ecos???
14. 假设CSNS高能输运线的质子束流横向分布为高斯分布,发射度为10 ? mm?mrad,束流功率为100 kW,某四极磁铁处水平方向的平均?函数为20 m,磁铁长度为0.5 m,如果要求此处水平方向的平均束流损失不超过1 W/m,则四极磁铁的最小孔径是多少? r0解方程??r01e2?x22?2dx?1?1[W/m]?0.5[m],得 100[kW]
r0?4.5648?
?4.5648?4.5648?20
?64.6[mm]
15. 已知束流初始参数为?x=?y=20 m,?x=?y=-0.3,一组三合一透镜组的布局为(D,QD,D,QF,D,QD,D),其中D为漂移节,长度均为1 m;QF为聚焦四极透镜,长度为0.2 m,聚焦强度为0.5 m-2;QD为散焦四极透镜,长度为0.1 m,聚焦强度为-0.6 m-2。
(1)画出束流经过这组三合一透镜组的束流包络图;
(2)如果要求束流在QF透镜中间处?x=?y=0,计算QF和QD的聚焦强度,并画出束流包络图;
(3)如果在三合一透镜组的末端增加一段漂移节,要求束流在末端的?x=?y=0,则增加的漂移节长度是多少?
(1)


(2)KQF=1.353602 m-2,KQD=-1.387554 m-2。

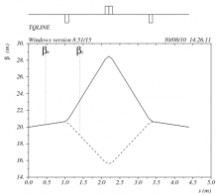
(3)L=5.504587 m
16. 已知初始束流参数为?x1=45.00 m, ?y1=1.12 m,?x1=?y1=0,在经过一段输运线后,出口的束流参数为?x2=147.00 m, ?y1=21.00 m,?x2=-11.7,?y2=4.0,出口和入口之间的相移为??x=0.463?2?,??y=0.676?2?,计算此段输运线的传输矩阵。

1.758770.142816
0000
18.73820.953007
0000001.941560.554127
00004.33490.722146
00000010
000001
17. CSNS高能输运线接受度为350 ? mm?mrad,计算内径为? 265 mm四极磁铁处可容许的最大?函数。
r0?amax
?max?r02
?a
(265/2)2
?350
?50.2m
18. 设电子束流初始能量为30 MeV,脉冲长度为5 ps,经过高频频率为2856 MHz的行波加速结构加速到1.9 GeV,同步加速相位始终保持在加速场峰值上,不考虑尾场效应,估算仅由束长引起的能量分散。 高频周期为T?1?350.14[ps], 62856?10
?E?1900?(30?(1900?30)?cos(
?1.88[MeV]
19. 推导能散5/2?2?)) 350.14?P?E和动量散度之间的关系。假设1.6 GeV质子束流的动量分散为0.3%,EP
计算对应的能散,如果是电子束流,则能散又是多少?
(1)
?? v
c
??1
??2
E??m0c2
P??m0v
???v3v?v???v 22c2cv?2c1
2?E??(m0c2)??2v?v22?v ???????22E?m0c?cvv
?P??(mv)??m?v?P?m0v
?3m0?2?v??m0?v??m0v
??2?2?1
?v
v
?E?P??2 EP??2
(2)质子束流能散: ???vv
??EtotalE0?Ek938.272[MeV]?1600[MeV]???2.70526 E0E0938.272[MeV]
???1
?2?0.929171
?E?P??2?0.259% EP
(3)电子束流能散:
??EtotalE0?Ek0.511[MeV]?1600[MeV]???3132.12 E0E00.511[MeV]
???1
?2?1
?E?P??2?0.3% EP
20.BEPC直线加速器长度为200m,采用的是SLAC型加速结构,每个加速单元的长度为
3.5cm,尾场函数为W0'(0)?6.3[V?pC?m],W0'(?1mm)?4.1[V?pC?m]。假设电子束流束团长度为1mm,电荷量为1.6 nC,估算双宏粒子模型下头部和尾部粒子因单束团尾场效应造成的能量损失。 ??1?1?1?1
?Eh??1N2eW0'(0?)22
11.6?10?9[nC]6.3[V]200[m]?????12??e 2210[C]3.5[cm]
??14.4[MeV]
?Et??1N2NeW0'(0?)?e2W0'(?1mm)222
11.6?10?9[nC]6.3[V]200[m]1.6?10?9[nC]4.1[V]200[m]?????12??e???12??e2210[C]3.5[cm]210[C]3.5[cm]??14.4[MeV]?18.7[MeV]
??33.1[MeV]
21.设飘移管型直线加速器工作模式为0模,飘移管之间的加速间隙宽度为g,假设加速场在其间近似为方波,推导渡越时间因子T?sin(?g??),其中?c为粒子相速,?为加速场?g??
波长。
因为是方波近似,所以Ez(z)不随z变化,即Ez(z)?Ez(0)
kz??
vz?2?cz2?z? ?v??
?T?g/2z?g/2
E(z)coskzdzEz(z)dz
cos2?z??g/2
?
?
Ez(0)?g/2?g/2??dz Ez(0)gsin(?g??)?g??
三 : 直线加速器
1. 假设宇宙线中的质子进入大气层时的能量为1焦耳,换算成TeV是多少,并计算质子的
速度和?。(www.61k.com]
1[J]?6.25?1018[eV]?6.25?106[TeV] ?191.6?10[C]
??E19 ??6.66?10?19E0938.272?1.6?10
???1
?2?1
v??c?c
2. 推导dEdP和之间的关系。 EP
?? v
c
??1
??2
E??m0c2
P??m0v
d??v3vdv??dv 22c2cv?2c1
2dEd?(m0c2)d?2vdv22dv ???????22E?m0c?cvv
dPd?(mv)??mdv?P?m0v
?3m0?2dv??m0dv??m0v
??2?2?1
dv
v
dEdP??2 EP??2
??dvv
直线加速 直线加速器
3. 地磁场约为1Gs,计算质子在多大速度时受到的磁场力与所受到的重力相当,并计算相
应的动能。(www.61k.com]
evB?mpg
1.67?10?27?9.8v???0.001[m/s] ?19eB1.6?10?0.0001
1Ek?mpv2?8?10?34[J]?5?10?15[eV] 2
4. CSNS打靶的质子束流能量为1.6 GeV,平均流强为62.5 ?A,计算束流的平均功率。 mpgP?I?Ek?e?I?Ek?62.5?10?6?1.6?109?100[kW] e
5. 加速器中为什么使用TM波用于加速,而不是TE波,是如何使相速小于光速的? TM波有纵向的电场分量可用于加速带电粒子,而TE波没有纵向电场分量。在圆波导中加入周期性的盘荷负载后,产生的空间谐波分量可提供小于或等于光速的相速。
6. BEPC直线加速器的行波加速结构的工作频率为2856 MHz,计算加速场的波长。
c3?108[m/s]????0.105[m] 6f2856?10[Hz]
7. 如果圆波导的直径2b从8.4 cm变化到8.2 cm,计算截止频率。
?cr1c13?108[m/s]fcr???2.405???2.405??2.8[GHz] 2?2?b2?4.1[cm]
8. 高频波长为λ= 12 cm的直线加速器,分别计算其?/2模、0模、2?/3模、?模的单元
(Cell)长度。
?/2模:Lc??
???2?/???2??12[cm]?3[cm] 4
0模:Lc??
2?/2??12[cm]?12[cm] 1
?12[cm]?4[cm] 32?/3模:Lc??
?2?2?/???3?
直线加速 直线加速器
?模:Lc??12[cm]??6[cm] 2?/?2
9. 设一行波电子直线加速器,为等梯度加速结构,结构的主要参数为: 工作频率f0?2998MHz,工作模式2?/3,每加速节长30?0,平均分路阻抗Zs?56M?/m,每节衰减常数?0?0.55;每节加速结构各有一功率源,它向加速结构输入的最大脉冲功率为30MW。[www.61k.com]
请回答下列问题:
(1) 加速结构的最大加速梯度是多少?
(2) 在每节加速结构的尾部的剩余输出功率是多少?
(3) 每节的最大能量增益是多少?
(4) 若将束流能量由20MeV加速到600MeV,需几节加速结构? 共有多少个加速单元?
(2)每节加速结构的尾部的剩余输出功率:
Pout?P0e?2?0
?30MW?e?2?0.55
?10MW
(1)单位长度的功率损失: P?P30MW?10MW?dP?????6.67MW/m ????dzL3m??
加速结构的最大加速梯度:
Ea??Zs
dP?56M?/m?6.67MW/m?19.33MV/m dz
(3)每节加速结构的长度为: c2.9979?108
L?30?0?30??30??3m 6f2998?10
每节加速结构的能量增益:
?W?eEaLcos00?e?19.33MV/m?3m?58MeV
直线加速 直线加速器
(4)将束流能量由20MeV加速到600MeV,所需加速结构数量:
N?600?20?10 58
每节加速结构的加速单元个数:30?3?90
所需加速单元总个数:90?10?900
10. 加速结构的分路阻抗由什么决定?等阻抗和等梯度加速结构有什么区别?
加速结构的分路阻抗决定于结构的形状、尺寸、材料和工作模式。(www.61k.com)
等阻抗加速结构每个单元的几何参数都一样,Q、vg、Zs和?0都相同,高频功率和电场沿传播方向指数衰减。
等梯度加速结构通过调整各加速腔的横向几何尺寸a和b,使得加速电场始终保持恒定。与等阻抗加速结构相比,在同样的能量增益的情况下,等梯度加速结构的能量损失均匀。
10. 设一质子直线加速器,工作频率为200 MHz, 渡越时间因子 T?0.85,同步相位为
?s??30o,初始速度 ??
v?0.15,束流相对于同步粒子的初始能量范围为 c?0.45MeV。 试求:为在纵向俘获该束流,要求加速器入口的加速电场至少多高?
33?2?2eET????m0c?(?cos??sin?)sss?2??m0c?1/2答: 纵向稳定区的最大能量范围?Wmax
不小于束流的能量范围, ,应
?2?E0(MV/m)?0.85?(0.15)3?(1.011)3?1.5m?0.45MeV?938MeV?(?0.52?0.866?(?0.5))?3.14?938MeV??1/2
0.45MeV?938MeV1.41?10?7E0
E0?
??1/2 0.451,E0?1.64MV/m ?7938.4?10
11. CSNS注入H-束流的能量为80 MeV,引出质子束流的能量为1.6 GeV,计算这两种情况
直线加速 直线加速器
下束流的磁刚度。[www.61k.com)
??EE?E ?E0E0
???1
?2
mv?mc2v? B????(E?E)0k2qqcc
c? 299792458[m/s]
(1) 注入H-束流:
H-的静止能量约为1个质子和2个电子静止能量的总和:
E0?938.272[MeV]?2?0.511[MeV]?938.783[MeV]
??1.08517
??0.388344
B??(E0?Ek)?
c?1.32037[T?m] (1.31946 [T?m])
(2)引出质子束流:
E0?938.272[MeV]
??2.70526
??0.929171
B??(E0?Ek)
12. CSNS高能输运线的工作能量为1.6 GeV,四极磁铁内径为?180 mm,磁铁极面场强最大为7000 Gs,求四极磁铁强度K的最大值。 ?c?7.86707[T?m] (1.86163 [T?m])
K?1?By1?B ?B??xB??y
直线加速 直线加速器
Kmax?
?1??By????B???x??max1gmaxB?
1Bmax ?B?r
10.7??7.86710.180/2
?0.9886[m?2]
13. 推导等梯度行波加速管在高能情况下(v=c)的横向传输矩阵。(www.61k.com) 高能情况下?E
E??2?P
P??P
P,
设加速管长度为L,束流在进入加速段前动量为P0,水平方向动量分量为P?x0,则
x'(0)?P?x0。 P0
在经过加速管后束流动量增加量为?P,则
PPx'(0)Px'(s)??? P0?1?1?LP0?LP0?L
x'(L)?x'(0) 1?P0
Lx(L)?x(0)??x'(s)ds0
?x(0)??L
0x'(0)ds1?P0?L
?x(0)?L?x'(0)?Pln(1?)?PP0
P0
表示成矩阵形式:
直线加速 直线加速器
??1??x(L)????x'(L)???????0???
传输矩阵为: L?P?ln(1?)??PP0???x(0)?P0???x'(0)?? 1????P?1??P0?
??1??R???0
???L?P?ln(1?)?P0?P0?? 1??1??P0?
考虑到加速管的加速相位,设能量增益为?E,则
E0?Ecos???ln(1?)??1L?Ecos?E0? R??E??0??E0??Ecos???
14. 假设CSNS高能输运线的质子束流横向分布为高斯分布,发射度为10 ? mm?mrad,束流功率为100 kW,某四极磁铁处水平方向的平均?函数为20 m,磁铁长度为0.5 m,如果要求此处水平方向的平均束流损失不超过1 W/m,则四极磁铁的最小孔径是多少? r0解方程??r01e2?x22?2dx?1?1[W/m]?0.5[m],得 100[kW]
r0?4.5648?
?4.5648?4.5648?20
?64.6[mm]
直线加速 直线加速器
15. 已知束流初始参数为?x=?y=20 m,?x=?y=-0.3,一组三合一透镜组的布局为(D,QD,D,QF,D,QD,D),其中D为漂移节,长度均为1 m;QF为聚焦四极透镜,长度为0.2 m,聚焦强度为0.5 m-2;QD为散焦四极透镜,长度为0.1 m,聚焦强度为-0.6 m-2。(www.61k.com)
(1)画出束流经过这组三合一透镜组的束流包络图;
(2)如果要求束流在QF透镜中间处?x=?y=0,计算QF和QD的聚焦强度,并画出束流包络图;
(3)如果在三合一透镜组的末端增加一段漂移节,要求束流在末端的?x=?y=0,则增加的漂移节长度是多少?
(1)
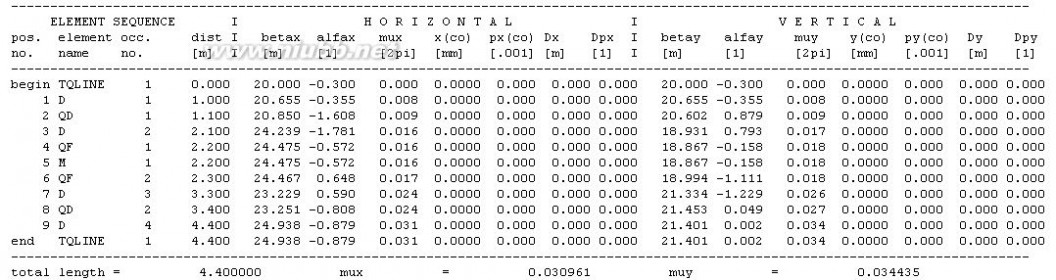
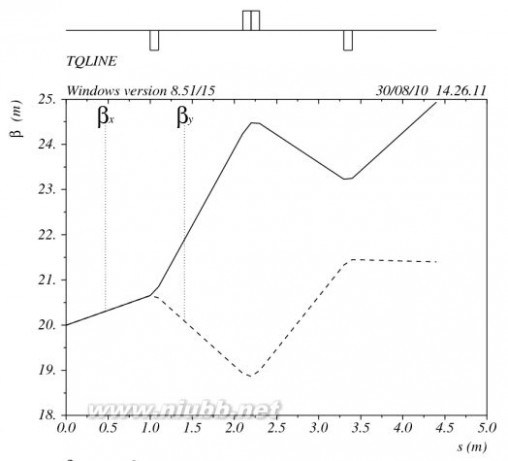
(2)KQF=1.353602 m-2,KQD=-1.387554 m-2。
直线加速 直线加速器
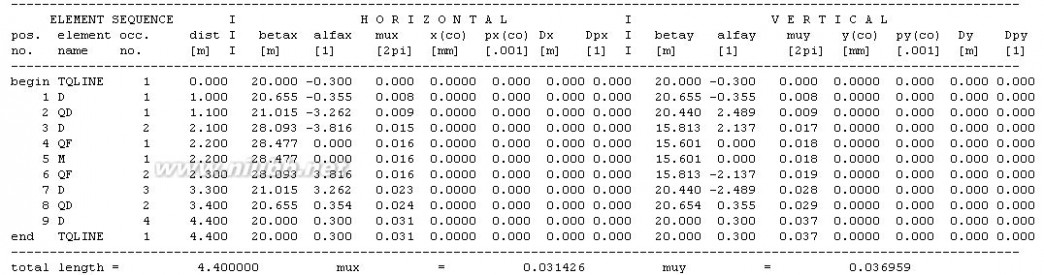

(3)L=5.504587 m
16. 已知初始束流参数为?x1=45.00 m, ?y1=1.12 m,?x1=?y1=0,在经过一段输运线后,出口的束流参数为?x2=147.00 m, ?y1=21.00 m,?x2=-11.7,?y2=4.0,出口和入口之间的相移为??x=0.463?2?,??y=0.676?2?,计算此段输运线的传输矩阵。[www.61k.com]
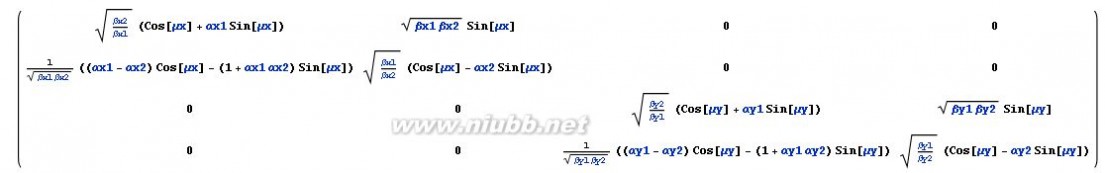
1.758770.142816
0000
18.73820.953007
0000001.941560.554127
00004.33490.722146
00000010
000001
17. CSNS高能输运线接受度为350 ? mm?mrad,计算内径为? 265 mm四极磁铁处可容许的最大?函数。
直线加速 直线加速器
r0?amax
?max?r02
?a
(265/2)2
?350
?50.2m
18. 设电子束流初始能量为30 MeV,脉冲长度为5 ps,经过高频频率为2856 MHz的行波加速结构加速到1.9 GeV,同步加速相位始终保持在加速场峰值上,不考虑尾场效应,估算仅由束长引起的能量分散。[www.61k.com] 高频周期为T?1?350.14[ps], 62856?10
?E?1900?(30?(1900?30)?cos(
?1.88[MeV]
19. 推导能散5/2?2?)) 350.14?P?E和动量散度之间的关系。假设1.6 GeV质子束流的动量分散为0.3%,EP
计算对应的能散,如果是电子束流,则能散又是多少?
(1)
?? v
c
??1
??2
E??m0c2
P??m0v
???v3v?v???v 22c2cv?2c1
直线加速 直线加速器
2?E??(m0c2)??2v?v22?v ???????22E?m0c?cvv
?P??(mv)??m?v?P?m0v
?3m0?2?v??m0?v??m0v
??2?2?1
?v
v
?E?P??2 EP??2
(2)质子束流能散: ???vv
??EtotalE0?Ek938.272[MeV]?1600[MeV]???2.70526 E0E0938.272[MeV]
???1
?2?0.929171
?E?P??2?0.259% EP
(3)电子束流能散:
??EtotalE0?Ek0.511[MeV]?1600[MeV]???3132.12 E0E00.511[MeV]
???1
?2?1
?E?P??2?0.3% EP
20.BEPC直线加速器长度为200m,采用的是SLAC型加速结构,每个加速单元的长度为
3.5cm,尾场函数为W0'(0)?6.3[V?pC?m],W0'(?1mm)?4.1[V?pC?m]。[www.61k.com)假设电子束流束团长度为1mm,电荷量为1.6 nC,估算双宏粒子模型下头部和尾部粒子因单束团尾场效应造成的能量损失。 ??1?1?1?1
直线加速 直线加速器
?Eh??1N2eW0'(0?)22
11.6?10?9[nC]6.3[V]200[m]?????12??e 2210[C]3.5[cm]
??14.4[MeV]
?Et??1N2NeW0'(0?)?e2W0'(?1mm)222
11.6?10?9[nC]6.3[V]200[m]1.6?10?9[nC]4.1[V]200[m]?????12??e???12??e2210[C]3.5[cm]210[C]3.5[cm]??14.4[MeV]?18.7[MeV]
??33.1[MeV]
21.设飘移管型直线加速器工作模式为0模,飘移管之间的加速间隙宽度为g,假设加速场在其间近似为方波,推导渡越时间因子T?sin(?g??),其中?c为粒子相速,?为加速场?g??
波长。[www.61k.com]
因为是方波近似,所以Ez(z)不随z变化,即Ez(z)?Ez(0)
kz??
vz?2?cz2?z? ?v??
?T?g/2z?g/2
E(z)coskzdzEz(z)dz
cos2?z??g/2
?
?
Ez(0)?g/2?g/2??dz Ez(0)gsin(?g??)?g??
本文标题:直线加速器-直线加速器:直线加速器-历史,直线加速器-原理61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1