一 : 大学生数学建模论文答辩指导

有很多参加大学数学建模竞赛的学生, 建模论文写得很好,数学模型建立的观点也很新颖独特,但一旦要答辩,心理就会变得惴惴不安,不知所措。 而且他们心理最大的疑问就是:“数学建模怎么进行答辩? 老师一般问什么问题? PPT 幻灯片怎么做? PPT 幻灯片上主要写些什么? ”针对这些问题,笔者拟从五个方面具体分析,期望对大学生数学建模论文答辩有所帮助。
www.niu(www.61k.com)bb.net一、建模论文答辩前应做的准备工作
大学生的建模论文基本上都有或多或少的缺点。 如文字表述的逻辑性、论文的规范性、图形的准确性等都有可能存在缺陷,只要论文上交给评委组了,以上存在的种种问题就无法再挽回了。 但是只要你的论文有创意、观点新颖,也有可能获得参加建模论文答辩的机会。 如果真的获得了答辩的机会,作为答辩的学生就应该高度重视,严肃认真地把握好这个机会, 要清楚自己论文形成的整个过程,这样参加答辩时才会头脑清晰。 笔者总结归纳了高教社杯全国大学生数学建模竞赛答辩前必须注意的问题,供参加数学建模答辩的学生参考。 包括以下内容:(1)论文的主题是什么? (2)你为何选择写这个主题的论文?(3) 论文的研究问题是什么 ? 为什么选择这个问题来研究? (4)掌握论文中涉及的基本理论;(5)对涉及的理论分析、方法、原则问题要熟练掌握;(6)陈述要全面、流利、简练(建议反复练习一下);(7)结合实践谈谈自己对该理论有何新的认识?(8)你所提出的解决方法,是否有应用的前景? (9)在写论文时,收集了哪些方面的资料,是怎样收集的?(10)论文最重要的参考文献是哪一篇? 请简单介绍其主要内容;(11)论文主要创新点有哪些? (12)你的研究存在哪些局限与不足? (13)论文所涉及的主题还可以从哪些方面进一步深入研究? (14)要特别熟悉论文的内容,一些名词尤其要注意, 比如你引用了平衡计分卡的内容或观点,一定要搞清是谁发明的,否则问起来回答不出来会打折扣的;(15)引用一些书名,最好是自己读过的,内容大概知道一些;(16)准备 10-15 分钟的答辩陈述,一定要把自己论文的关键之处说清楚,让评委老师眼前一亮;(17)可能抛开论文以外 ,问你几个与学习工作相关的话题。
如果在参加建模论文答辩前能够把握好以上问题,说明你已经准备得不错了。
二、数学建模答辩时应注意的问题
答辩流程分为论文方案讲解和专家评委提问两个环节,每个环节限时七、八分钟。 在比赛中,各参赛队伍的表述都要求条理清晰,思维严谨,对同样的问题从不同的角度,通过不同的数学模型进行讲解。 但要注意以下几点:(1)答辩的过程就是检验你的真实建模能力 ,同时也检测你的建模论文是不是自己做的。 所以答辩时一定要证明论文是自己做的。 (2)答辩也就是要求陈述你的建模过程以及建模的创新点,所以答辩时要把做题的思路讲清楚,每个步骤都必须严谨。 (3)制作 PPT 幻灯片尽量多用图,少用文字。 (4)对于自己的建模论文,多设计几个问题,并有针对性地给出合理的解释, 防止到时提问时不知道怎么回答。 (5)一定要坚信自己的模型是合理正确的,否则别人也就不会相信你。 评委对你的模型肯定要提问,要你说理由, 你只要大胆说出你的方法和模型的特色就可以了。 (6)回答教师提问时一定要谦虚,有争议的问题,可以商榷,不要争辩。 (7)自己最好准备一份论文打印稿备份在手,以备随时查阅。 (8)答辩时千万不能紧张,一定要口齿清晰。 (9)不管评委老师问的问题有多么刁钻、有多么难以回答,都要保持微笑。 即使没有圆满回答出评委老师问的问题,也要保持微笑,给评委老师一个良好的印象,把评委老师那份感情分牢牢地抓在手里(犇_嫑)。
三、建模答辩时要反思自己的论文形成过程
笔者认为,大学生数学建模竞赛论文答辩并不可怕,可怕的是参赛学生是否有参加答辩的能力, 这种能力来源于参赛学生建模论文的形成过程。 因为学生几十页的建模论文不是苍白文字的罗列, 而是学生团体合作的结果。 他们从拿到竞赛题目的茫然不知到对题目思路由模糊到清晰,直到能够建立数学模型,最后解决题目要解决的问题。 在这个过程中,论文里的所有数学模型、解决问题的计算方法、 提出解决问题的方案等都是学生亲身的经历和体验,可以说建模论文是学生三天劳动的结晶,所以建模论文只要是学生自己做出来的,答辩就不是问题,因为论文中的所有片段会像幻灯片一样在学生的头脑中放映,所以不管评委老师提什么问题,选手只要沉着冷静就能对答如流。
四、建模答辩要尽量体现建模思想、逻辑和价值性
数学建模一般没有标准答案, 竞赛的目的也是在挖掘解决问题的最优方案。 建模可发挥的空间比较大,可以从不同的角度、用不同的方法去解决同一个问题,但答辩的宗旨是一致的,即答辩的问题主要集中在建模的思想、逻辑性及应用的价值性上。 也就是说怎样证明你建的数学模型是最优的。建模的答辩时间一般只有 15 分钟, 学生最多有 10分钟的时间简述自己的论文观点, 剩下的时间由评委提问。 评委有可能问一些建模里没有考虑清楚或说明清楚的问题,指出漏洞,甚至“刁难”,不过这个主要是考察建模论文是不是学生自己做的。 所以答辩的学生只要不慌,充满信心,回答评委问题时,口齿清晰,逻辑推理性强,就一定会成功。
五、建模答辩幻灯片(PPT)的制作
PPT 就是幻灯片 。 可以理解把一张一张 “图片 ”放给别人看。 也就是把你想告诉别人的东西,排版起来,介绍给别人,PPT 重要的还是内容,格式只是表现形式。
在答辩过程中, 精彩的 PPT 幻灯片会抓住评委的注意力,令评委们耳目一新。 由于答辩时间总共不超过 15分钟,学生简述时间约 10 分钟,在这短短的时间内把你三天的建模工作简述出来, 是对学生综合能力和表达能力的挑战。 所以制作好 PPT 幻灯片是答辩成功的重要环节。 一般应注意以下几点:(1)15 分钟的答辩准备大约20-30 页幻灯片即可。 每页只用 8-10 行字,或一幅图。 只列出要点及关键技术。 (2)幻灯片中不要出现参赛学校名称等信息。 (3)幻灯片的背景不要追求花哨,尽量用浅色调(米黄、象牙百、灰色等),不要弄些与答辩无关的动画。(4)幻灯片一般从建模的提要 、提出问题 、分析问题 、解决问题入手制作。 (5)幻灯片内容要突出自己的建模特点。主要体现建模的思想、算法、特殊技术及创新点。 (6)答辩者大约一分钟讲 2 页,听众一分钟大约看完 4-5 页。 不能完全照着幻灯片念,要用口语化、演讲式的语言讲。 (7)充分利用图形,在较短时间内传递较多信息。 (8)给幻灯片加上页码,再打开母版,把“#”改成“#/X”,X 是幻灯片的总页数, 这样答辩时就能知道已讲了多少, 便于调整速度。 (9)如果能用动画把论文中的图形动态变化部分动态演示出来,会使答辩更精彩,更能形象说明论文的论点。
总之,答辩的同学一定要准备充分,阐述所建模型与实际生活的联系,而且要不乏趣味性。 在答辩过程中评委可能从模型的抽象到模型的构建向答辩的同学提出很多启发性的问题, 引导大家深入思考如何构建一个合理标准的数学模型。

二 : 全国大学生数学建模论文
题目:悬崖跳水的水池深度
【摘要】
高空跳水是一种惊险刺激的体育运动项目,此文主要研究高台跳水和高空跳水与水深的关系,从而保证运动员达到一定的安全性。高空跳水是一项极限运动,在空中“飞行”的时间只有几秒钟,期间要表演一系列的扭腰和转身动作。运动员入水速度约为每小時78至100公里,人在进入水中的瞬间,水对身体的冲击相当于开车以每小时100公里的速度撞墙。如果跳水员是脑袋先落入水中,可能引起脑震荡甚至死亡,所以选手在完成动作后,必须脚部先入水。因此,我们建立一个跳水优化模型来定量的计算所需水池深度及跳台高度的安全性,从而使跳水运动有个较安全通道系数,这对国际跳水运动有着非常重要价值意义。
在建立跳水模型时,本文利用了流体力学和流固碰撞等相关知识,并通过公d2hdv式m求解出在不同跳台高度时??A??gsH?mg等,2dtdh
的水池的深度,才能保证运动员的安全。
在解决问题一时,我们将运动员的体重看作定量,把人体模型,优化成一个圆柱体从而简化我们的计算。整个过程分为三个阶段,入水前,入水后,及完全入水。然后从流体力学的角度分析不同条件可以分别用动能守恒定理,动量守恒定理,自由落体等公式,最后我们可得到上述微分方程。然后再用Matlab解微分方程及用plot绘出它相应的图象,从而得到我们想要一些数据。最终通过上述模型可分别求出男子和女子在不同跳台高度l所对应的水池深度h2(见表一),从而可以得出跳台高度l和水池深度h2的关系并用以及用图象更好的反应它们
之间的关系。
在解决问题二时,我们将跳台的高度看作定量,结合问题一的分析,与问题一分析类似,就是变量稍有不同,我们也可以通过上述相应的办法来求出男子和女子在不同体重m所对应的水池深度h2(见表二),从而可以得出体重m和水池
深度h2的关系及用图象来绘出它们的关系。
关键词:流固碰撞 流体力学 动能守恒定律 动量守恒定律 微分方程
1
1、 问题的重述与分析
1.1 问题的重述
悬崖跳水是一种惊险刺激的体育运动项目,通行的比赛规则要求,男子起跳高度为23至28米,女子起跳高度为18至23米。我国福建连城的冠豸山就举行过这样的比赛,那里的跳台高度是男子28米,女子20米。
近年来世界上新兴一种跳水比赛叫红牛悬崖跳水世界杯比赛,是一种非常危险、挑战人类极限的比赛。由于高空跳水危险性较大,容易出现伤害事故,所以在世界上开展得不很普遍。如何减小跳水当中的危害,提高安全性?因此需要我们建立数学模型,而我们要的工作就是:
1. 定量的计算,跳台下面的水池要有多深,才能保证人的安全;
2. 分析两个体重不同的人跳水时哪个需要更深的水。
1.2 问题的分析
要探讨水深的安全的问题,需要分析在跳水者进入水之后继续下落的深度,考虑到绝对的安全,那么在运动员下落至水底之前,速度减为足够小,而不至于因撞击池底而受伤。在本问题中,要确保运动员的绝对安全,此处所需深度恰好是运动员在水下首次静止时的深度。
空气中的下落按照质点下落分析,而将整个入水过程分成三个阶段如下: ① 接触水面碰撞,
② 人体与水面碰撞完毕后整个身体进入水中,
③ 整个身体刚好完全进入水中到触底。
第一个过程,人水短暂碰撞过程按照流固撞击处理,运用动力学原理能量和动量分析;
第二个过程,人的身体处于进入水的过程,建立运动状态方程;
第三个过程,由于身体完全进入水中,同样建立第二个状态方程;
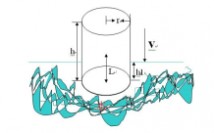
图1. 人体的简化模型
2
图2.跳水示意图
2、 问题的假设
1.人和水的接触面积适当,不会产生危险
2.人都经过了合格的训练,动作规范
3. 跳水的水池足够宽
4. 人体入水前,速度垂直向下,人体方向竖直向下,水平方向速度为0,水面静止。
5.落水时,双脚先着陆水
6.不考虑水流影响及气侯导致水平面上升的影响
7. 男子为底面半径为15cm,高为180cm的圆柱体,质量分布均匀,体重m=60kg 女子为底面半径为12cm,高为170cm的圆柱体,质量分布均匀,体重m=50kg
3、符号说明
g?9.8m/s2 为重力加速度,
??103kg/m3 为水的密度,
m=60kg 为人的质量,
l为跳台与水面的距离,
3

h为人体腾空高度,
v0为人即将与水面接触时的速度,
v1为人完全进入水时的速度,
v2是人水碰撞之后水的速度,
s为人体等效圆柱体的底面积,
r为柱体底面半径,
?t为人水撞击持续的时间,
H为人的高度,
A为柱体表面积,
?为粘滞系数,
h1代表柱体部分进入水面时底面与水面的距离,
h2代表柱体完全进入水面后底面与水面的距离。
4、模型的建立与求解
4.1 问题1的求解
对于体重m?60kg的男子从跳台高度为l(23~28m)的跳台跳水,已知l1?23m,h?0.3m,则有
①入水前:
22g(l?h)?v0
解得:v0?21.3701
②入水后:
d2hdv1m??A??gsh1?mg dt2dh1
0?h1?1.8m
h1(0)?0
dh1(0))?v0 dt
运用matlab求解微分方程得: (
h1(t)?exp(7/100*2355^(1/2)*t)*(213701/3297000*2355^(1/2)-200/471)+exp(-7/100*2355^(1/2)*t)*(-200/471-213701/3297000*2355^(1/2))+400/471 将h1(t)?H代入解得t?0.0847
4
dh2(t)
)t?0.0847?10.2560 dt
③完全浸入水中 v1?(
d2h2?vm??A??gsH?mg
dt2?h2
h2?1.8m
dh2(0)
?v1 dt
运用matlab求解微分方程得:
h2(t)?9/5-50000000/139*log(1/59569644531250000*(-1860793*sin(7/1000000*311221^(1/2)*t
)+437500*cos(7/1000000*311221^(1/2)*t)*311221^(1/2))^2)
令
dh2(t)
?0得t?0.9231 dt
则:h2?5.65
同理可得表1


5
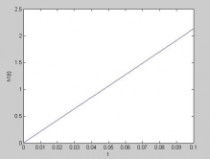
图3. h1与t的关系
4.2 问题2的求解
对于不同体重m(50~60kg)的人从一定的跳台高度l=23m的跳台跳水,已知l=23m,h?0.3m,m?50kg,则有 ①入水前:
22g(l?h)?v0
解得 v0?21.3701
②入水后:
d2hdv1m??A??gsh1?mg 2dtdh1
0?h1?1.8m
h1(0)?0
dh1(0))?v0 dt
运用matlab求解微分方程得: (
6
h1(t)?2137/6594*sin(21/100*314^(1/2)*t)*2^(1/2)*157^(1/2)-1000/1413*cos(21/100*314^(1/2)*t)+1000/1413
将h1(t)?H代入解得t=0.0780
dh2(t))t?0.0780?10.0121 dt
③完全浸入水中 v1?(
d2h2?vm??A??gsH?mg 2dt?h2
h2?1.8m
dh2(0)?v1 dt
运用matlab求解微分方程得:
h2(t)?-687/100*t^2+53663/2500*t+17/10 令dh2(t)?0得t=0.7278 dt
则:h2=6.3390
同理可得表2

5、模型的评价
优点:
1、本文的模型在建立过程中充分运用了流体力学中的知识,结合公式有效的处理跳水时的复杂问题,且适用性强。
2、我们还采用图形结合,形象生动的展现出跳水复杂过程。
3、我们仔细分析并推敲问题一和问题二之间的区别与联系。
4、在解决问题时,充分应用MATLAB软件,灵活地解决了繁杂方程的求解。 不足:
1、在考虑人在空气中的下落时,我们将人看作质点,忽略了其中的空气阻力,这样存在一定的精度影响。
2、在考虑人在水中的运动时,也忽略了一些重要的因素(如:水的粘度等),必 7
然会带来较大的误差,影响最终结果。
参考文献
[1] 丁祖荣,《流体力学(上册)》,高等教育出版社,2003,12.
[2] HakunaGone,跳水安全问题的分析,,2011-7-8.
[3] 姜启源等,数学建模(第3版),北京:高等教育出版社,2003.8.
[4] 有道词典,悬崖跳水,http://dict.youdao.com/search?q=bk%3A%E6%82%AC%E5%B4%96%E8%B7%B3%E6%B0%B4&keyfrom=wiki.index.results#q%3Dbk%253A%25E6%2582%25AC%25E5%25B4%2596%25E8%25B7%25B3%25E6%25B0%25B4%26keyfrom%3Dwiki.index.results,2011-7-8.
8
三 : 全国大学生数学建模论文
题目:悬崖跳水的水池深度
【摘要】
高空跳水是一种惊险刺激的体育运动项目,此文主要研究高台跳水和高空跳水与水深的关系,从而保证运动员达到一定的安全性。[www.61k.com]高空跳水是一项极限运动,在空中“飞行”的时间只有几秒钟,期间要表演一系列的扭腰和转身动作。运动员入水速度约为每小時78至100公里,人在进入水中的瞬间,水对身体的冲击相当于开车以每小时100公里的速度撞墙。如果跳水员是脑袋先落入水中,可能引起脑震荡甚至死亡,所以选手在完成动作后,必须脚部先入水。因此,我们建立一个跳水优化模型来定量的计算所需水池深度及跳台高度的安全性,从而使跳水运动有个较安全通道系数,这对国际跳水运动有着非常重要价值意义。
在建立跳水模型时,本文利用了流体力学和流固碰撞等相关知识,并通过公d2hdv式m求解出在不同跳台高度时??A??gsH?mg等,2dtdh
的水池的深度,才能保证运动员的安全。
在解决问题一时,我们将运动员的体重看作定量,把人体模型,优化成一个圆柱体从而简化我们的计算。整个过程分为三个阶段,入水前,入水后,及完全入水。然后从流体力学的角度分析不同条件可以分别用动能守恒定理,动量守恒定理,自由落体等公式,最后我们可得到上述微分方程。然后再用Matlab解微分方程及用plot绘出它相应的图象,从而得到我们想要一些数据。最终通过上述模型可分别求出男子和女子在不同跳台高度l所对应的水池深度h2(见表一),从而可以得出跳台高度l和水池深度h2的关系并用以及用图象更好的反应它们
之间的关系。
在解决问题二时,我们将跳台的高度看作定量,结合问题一的分析,与问题一分析类似,就是变量稍有不同,我们也可以通过上述相应的办法来求出男子和女子在不同体重m所对应的水池深度h2(见表二),从而可以得出体重m和水池
深度h2的关系及用图象来绘出它们的关系。
关键词:流固碰撞 流体力学 动能守恒定律 动量守恒定律 微分方程
1
大学生数学建模论文 全国大学生数学建模论文
1、 问题的重述与分析
1.1 问题的重述
悬崖跳水是一种惊险刺激的体育运动项目,通行的比赛规则要求,男子起跳高度为23至28米,女子起跳高度为18至23米。(www.61k.com]我国福建连城的冠豸山就举行过这样的比赛,那里的跳台高度是男子28米,女子20米。
近年来世界上新兴一种跳水比赛叫红牛悬崖跳水世界杯比赛,是一种非常危险、挑战人类极限的比赛。由于高空跳水危险性较大,容易出现伤害事故,所以在世界上开展得不很普遍。如何减小跳水当中的危害,提高安全性?因此需要我们建立数学模型,而我们要的工作就是:
1. 定量的计算,跳台下面的水池要有多深,才能保证人的安全;
2. 分析两个体重不同的人跳水时哪个需要更深的水。
1.2 问题的分析
要探讨水深的安全的问题,需要分析在跳水者进入水之后继续下落的深度,考虑到绝对的安全,那么在运动员下落至水底之前,速度减为足够小,而不至于因撞击池底而受伤。在本问题中,要确保运动员的绝对安全,此处所需深度恰好是运动员在水下首次静止时的深度。
空气中的下落按照质点下落分析,而将整个入水过程分成三个阶段如下: ① 接触水面碰撞,
② 人体与水面碰撞完毕后整个身体进入水中,
③ 整个身体刚好完全进入水中到触底。
第一个过程,人水短暂碰撞过程按照流固撞击处理,运用动力学原理能量和动量分析;
第二个过程,人的身体处于进入水的过程,建立运动状态方程;
第三个过程,由于身体完全进入水中,同样建立第二个状态方程;
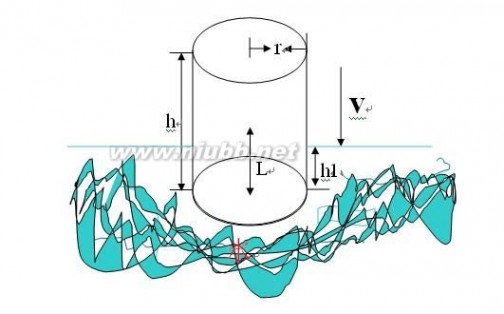
图1. 人体的简化模型
2
大学生数学建模论文 全国大学生数学建模论文
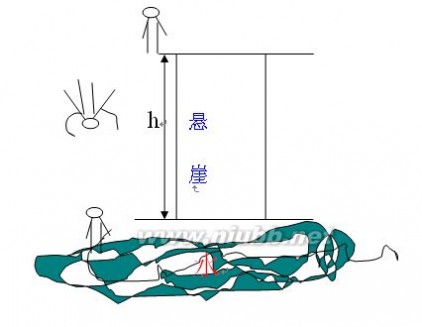
图2.跳水示意图
2、 问题的假设
1.人和水的接触面积适当,不会产生危险
2.人都经过了合格的训练,动作规范
3. 跳水的水池足够宽
4. 人体入水前,速度垂直向下,人体方向竖直向下,水平方向速度为0,水面静止。(www.61k.com]
5.落水时,双脚先着陆水
6.不考虑水流影响及气侯导致水平面上升的影响
7. 男子为底面半径为15cm,高为180cm的圆柱体,质量分布均匀,体重m=60kg 女子为底面半径为12cm,高为170cm的圆柱体,质量分布均匀,体重m=50kg
3、符号说明
g?9.8m/s2 为重力加速度,
??103kg/m3 为水的密度,
m=60kg 为人的质量,
l为跳台与水面的距离,
3
大学生数学建模论文 全国大学生数学建模论文
h为人体腾空高度,
v0为人即将与水面接触时的速度,
v1为人完全进入水时的速度,
v2是人水碰撞之后水的速度,
s为人体等效圆柱体的底面积,
r为柱体底面半径,
?t为人水撞击持续的时间,
H为人的高度,
A为柱体表面积,
?为粘滞系数,
h1代表柱体部分进入水面时底面与水面的距离,
h2代表柱体完全进入水面后底面与水面的距离。(www.61k.com)
4、模型的建立与求解
4.1 问题1的求解
对于体重m?60kg的男子从跳台高度为l(23~28m)的跳台跳水,已知l1?23m,h?0.3m,则有
①入水前:
22g(l?h)?v0
解得:v0?21.3701
②入水后:
d2hdv1m??A??gsh1?mg dt2dh1
0?h1?1.8m
h1(0)?0
dh1(0))?v0 dt
运用matlab求解微分方程得: (
h1(t)?exp(7/100*2355^(1/2)*t)*(213701/3297000*2355^(1/2)-200/471)+exp(-7/100*2355^(1/2)*t)*(-200/471-213701/3297000*2355^(1/2))+400/471 将h1(t)?H代入解得t?0.0847
4
大学生数学建模论文 全国大学生数学建模论文
dh2(t)
)t?0.0847?10.2560 dt
③完全浸入水中 v1?(
d2h2?vm??A??gsH?mg
dt2?h2
h2?1.8m
dh2(0)
?v1 dt
运用matlab求解微分方程得:
h2(t)?9/5-50000000/139*log(1/59569644531250000*(-1860793*sin(7/1000000*311221^(1/2)*t
)+437500*cos(7/1000000*311221^(1/2)*t)*311221^(1/2))^2)
令
dh2(t)
?0得t?0.9231 dt
则:h2?5.65
同理可得表1


5
大学生数学建模论文 全国大学生数学建模论文
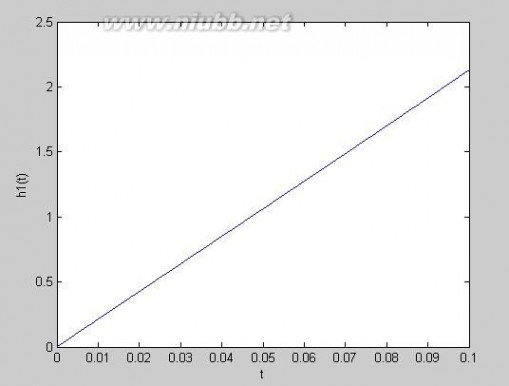
图3. h1与t的关系
4.2 问题2的求解
对于不同体重m(50~60kg)的人从一定的跳台高度l=23m的跳台跳水,已知l=23m,h?0.3m,m?50kg,则有 ①入水前:
22g(l?h)?v0
解得 v0?21.3701
②入水后:
d2hdv1m??A??gsh1?mg 2dtdh1
0?h1?1.8m
h1(0)?0
dh1(0))?v0 dt
运用matlab求解微分方程得: (
6
大学生数学建模论文 全国大学生数学建模论文
h1(t)?2137/6594*sin(21/100*314^(1/2)*t)*2^(1/2)*157^(1/2)-1000/1413*cos(21/100*314^(1/2)*t)+1000/1413
将h1(t)?H代入解得t=0.0780
dh2(t))t?0.0780?10.0121 dt
③完全浸入水中 v1?(
d2h2?vm??A??gsH?mg 2dt?h2
h2?1.8m
dh2(0)?v1 dt
运用matlab求解微分方程得:
h2(t)?-687/100*t^2+53663/2500*t+17/10 令dh2(t)?0得t=0.7278 dt
则:h2=6.3390
同理可得表2

5、模型的评价
优点:
1、本文的模型在建立过程中充分运用了流体力学中的知识,结合公式有效的处理跳水时的复杂问题,且适用性强。[www.61k.com)
2、我们还采用图形结合,形象生动的展现出跳水复杂过程。
3、我们仔细分析并推敲问题一和问题二之间的区别与联系。
4、在解决问题时,充分应用MATLAB软件,灵活地解决了繁杂方程的求解。 不足:
1、在考虑人在空气中的下落时,我们将人看作质点,忽略了其中的空气阻力,这样存在一定的精度影响。
2、在考虑人在水中的运动时,也忽略了一些重要的因素(如:水的粘度等),必 7
大学生数学建模论文 全国大学生数学建模论文
然会带来较大的误差,影响最终结果。[www.61k.com]
参考文献
[1] 丁祖荣,《流体力学(上册)》,高等教育出版社,2003,12.
[2] HakunaGone,跳水安全问题的分析,,2011-7-8.
[3] 姜启源等,数学建模(第3版),北京:高等教育出版社,2003.8.
[4] 有道词典,悬崖跳水,http://dict.youdao.com/search?q=bk%3A%E6%82%AC%E5%B4%96%E8%B7%B3%E6%B0%B4&keyfrom=wiki.index.results#q%3Dbk%253A%25E6%2582%25AC%25E5%25B4%2596%25E8%25B7%25B3%25E6%25B0%25B4%26keyfrom%3Dwiki.index.results,2011-7-8.
8
四 : 大学生数学建模论文答辩
有很多参加大学数学建模竞赛的学生, 建模论文写得很好,数学模型建立的观点也很新颖独特,但一旦要答辩,心理就会变得惴惴不安,不知所措。 而且他们心理最大的疑问就是:“数学建模怎么进行答辩? 老师一般问什么问题? ppt 幻灯片怎么做? ppt 幻灯片上主要写些什么? ”针对这些问题,笔者拟从五个方面具体分析,期望对大学生数学建模论文答辩有所帮助。
一、建模论文答辩前应做的准备工作
大学生的建模论文基本上都有或多或少的缺点。 如文字表述的逻辑性、论文的规范性、图形的准确性等都有可能存在缺陷,只要论文上交给评委组了,以上存在的种种问题就无法再挽回了。 但是只要你的论文有创意、观点新颖,也有可能获得参加建模论文答辩的机会。 如果真的获得了答辩的机会,作为答辩的学生就应该高度重视,严肃认真地把握好这个机会, 要清楚自己论文形成的整个过程,这样参加答辩时才会头脑清晰。 笔者总结归纳了高教社杯全国大学生数学建模竞赛答辩前必须注意的问题,供参加数学建模答辩的学生参考。 包括以下内容:(1)论文的主题是什么? (2)你为何选择写这个主题的论文?(3) 论文的研究问题是什么 ? 为什么选择这个问题来研究? (4)掌握论文中涉及的基本理论;(5)对涉及的理论分析、方法、原则问题要熟练掌握;(6)陈述要全面、流利、简练(建议反复练习一下);(7)结合实践谈谈自己对该理论有何新的认识?(8)你所提出的解决方法,是否有应用的前景? (9)在写论文时,收集了哪些方面的资料,是怎样收集的?(10)论文最重要的参考文献是哪一篇? 请简单介绍其主要内容;(11)论文主要创新点有哪些? (12)你的研究存在哪些局限与不足? (13)论文所涉及的主题还可以从哪些方面进一步深入研究? (14)要特别熟悉论文的内容,一些名词尤其要注意, 比如你引用了平衡计分卡的内容或观点,一定要搞清是谁发明的,否则问起来回答不出来会打折扣的;(15)引用一些书名,最好是自己读过的,内容大概知道一些;(16)准备 10-15 分钟的答辩陈述,一定要把自己论文的关键之处说清楚,让评委老师眼前一亮;(17)可能抛开论文以外 ,问你几个与学习工作相关的话题。
如果在参加建模论文答辩前能够把握好以上问题,说明你已经准备得不错了。
二、数学建模答辩时应注意的问题
答辩流程分为论文方案讲解和专家评委提问两个环节,每个环节限时七、八分钟。 在比赛中,各参赛队伍的表述都要求条理清晰,思维严谨,对同样的问题从不同的角度,通过不同的数学模型进行讲解。 但要注意以下几点:(1)答辩的过程就是检验你的真实建模能力 ,同时也检测你的建模论文是不是自己做的。 所以答辩时一定要证明论文是自己做的。 (2)答辩也就是要求陈述你的建模过程以及建模的创新点,所以答辩时要把做题的思路讲清楚,每个步骤都必须严谨。 (3)制作 ppt 幻灯片尽量多用图,少用文字。 (4)对于自己的建模论文,多设计几个问题,并有针对性地给出合理的解释, 防止到时提问时不知道怎么回答。 (5)一定要坚信自己的模型是合理正确的,否则别人也就不会相信你。 评委对你的模型肯定要提问,要你说理由, 你只要大胆说出你的方法和模型的特色就可以了。 (6)回答教师提问时一定要谦虚,有争议的问题,可以商榷,不要争辩。 (7)自己最好准备一份论文打印稿备份在手,以备随时查阅。 (8)答辩时千万不能紧张,一定要口齿清晰。 (9)不管评委老师问的问题有多么刁钻、有多么难以回答,都要保持微笑。 即使没有圆满回答出评委老师问的问题,也要保持微笑,给评委老师一个良好的印象,把评委老师那份感情分牢牢地抓在手里。
三、建模答辩时要反思自己的论文形成过程
笔者认为,大学生数学建模竞赛论文答辩并不可怕,可怕的是参赛学生是否有参加答辩的能力, 这种能力来源于参赛学生建模论文的形成过程。 因为学生几十页的建模论文不是苍白文字的罗列, 而是学生团体合作的结果。 他们从拿到竞赛题目的茫然不知到对题目思路由模糊到清晰,直到能够建立数学模型,最后解决题目要解决的问题。 在这个过程中,论文里的所有数学模型、解决问题的计算方法、 提出解决问题的方案等都是学生亲身的经历和体验,可以说建模论文是学生三天劳动的结晶,所以建模论文只要是学生自己做出来的,答辩就不是问题,因为论文中的所有片段会像幻灯片一样在学生的头脑中放映,所以不管评委老师提什么问题,选手只要沉着冷静就能对答如流。
四、建模答辩要尽量体现建模思想、逻辑和价值性
数学建模一般没有标准答案, 竞赛的目的也是在挖掘解决问题的最优方案。 建模可发挥的空间比较大,可以从不同的角度、用不同的方法去解决同一个问题,但答辩的宗旨是一致的,即答辩的问题主要集中在建模的思想、逻辑性及应用的价值性上。 也就是说怎样证明你建的数学模型是最优的。建模的答辩时间一般只有 15 分钟, 学生最多有 10分钟的时间简述自己的论文观点, 剩下的时间由评委提问。 评委有可能问一些建模里没有考虑清楚或说明清楚的问题,指出漏洞,甚至“刁难”,不过这个主要是考察建模论文是不是学生自己做的。 所以答辩的学生只要不慌,充满信心,回答评委问题时,口齿清晰,逻辑推理性强,就一定会成功。
五、建模答辩幻灯片(ppt)的制作
ppt 就是幻灯片 。 可以理解把一张一张 “图片 ”放给别人看。 也就是把你想告诉别人的东西,排版起来,介绍给别人,ppt 重要的还是内容,格式只是表现形式。
在答辩过程中, 精彩的 ppt 幻灯片会抓住评委的注意力,令评委们耳目一新。 由于答辩时间总共不超过 15分钟,学生简述时间约 10 分钟,在这短短的时间内把你三天的建模工作简述出来, 是对学生综合能力和表达能力的挑战。 所以制作好 ppt 幻灯片是答辩成功的重要环节。 一般应注意以下几点:(1)15 分钟的答辩准备大约20-30 页幻灯片即可。 每页只用 8-10 行字,或一幅图。 只列出要点及关键技术。 (2)幻灯片中不要出现参赛学校名称等信息。 (3)幻灯片的背景不要追求花哨,尽量用浅色调(米黄、象牙百、灰色等),不要弄些与答辩无关的动画。(4)幻灯片一般从建模的提要 、提出问题 、分析问题 、解决问题入手制作。 (5)幻灯片内容要突出自己的建模特点。主要体现建模的思想、算法、特殊技术及创新点。 (6)答辩者大约一分钟讲 2 页,听众一分钟大约看完 4-5 页。 不能完全照着幻灯片念,要用口语化、演讲式的语言讲。 (7)充分利用图形,在较短时间内传递较多信息。 (8)给幻灯片加上页码,再打开母版,把“#”改成“#/x”,x 是幻灯片的总页数, 这样答辩时就能知道已讲了多少, 便于调整速度。 (9)如果能用动画把论文中的图形动态变化部分动态演示出来,会使答辩更精彩,更能形象说明论文的论点。
总之,答辩的同学一定要准备充分,阐述所建模型与实际生活的联系,而且要不乏趣味性。 在答辩过程中评委可能从模型的抽象到模型的构建向答辩的同学提出很多启发性的问题, 引导大家深入思考如何构建一个合理标准的数学模型。
本文标题:大学生数学建模论文-大学生数学建模论文答辩指导61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1