一 : 哈夫曼树：哈夫曼树-基本术语，哈夫曼树-结构构造

给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman tree)。哈夫曼树也可以是k叉的，只是在构造k叉哈夫曼树时需要先进行一些调整。构造哈夫曼树的思想是每次选k个权重最小的元素来合成一个新的元素，该元素权重为k个元素权重之和。但是当k大于2时，按照这个步骤做下去可能到最后剩下的元素少于k个。解决这个问题的办法是假设已经有了一棵哈夫曼树(且为一棵满k叉树)，则可以计算出其叶节点数目为(k-1)nk+1,式子中的nk表示子节点数目为k的节点数目。于是对给定的n个权值构造k叉哈夫曼树时,可以先考虑增加一些权值为0的叶子节点，使得叶子节点总数为(k-1)nk+1这种形式,然后再按照哈夫曼树的方法进行构造即可。

哈夫曼树_哈夫曼树 -基本术语

哈夫曼树又叫为最优树.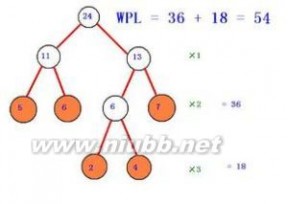

哈夫曼树1、路径和路径长度
在一棵树中，从1个结点往下可以达到的孩子或子孙结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。
2、结点的权及带权路径长度
若将树中结点赋给1个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。
3、树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为wpl。

哈夫曼树_哈夫曼树 -结构构造

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：
(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有1个结点)；
(2) 在森林中选出2个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；
(3)从森林中删除选取的两棵树，并将新树加入森林；
(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

哈夫曼树_哈夫曼树 -相关应用

哈夫曼编码

在数据通信中，需要将传送的文字转换成二进制的字符串，用0，1码的不同排列来表示字符。例如，需传送的报文为“AFTER DATA EAR ARE ART AREA”，这里用到的字符集为“A，E，R，T，F，D”，各字母出现的次数为{8，4，5，3，1，1}。现要求为这些字母设计编码。要区别六个字母，最简单的二进制编码方式是等长编码，固定采用3位二进制，可分别用000、001、010、011、100、101对“A，E，R，T，F，D”进行编码发送，当对方接收报文时再按照三位一分进行译码。显然编码的长度取决报文中不同字符的个数。若报文中可能出现二十六个不同字符，则固定编码长度为5。然而，传送报文时总是希望总长度尽可能短。在实际应用中，各个字符的出现频度或使用次数是不相同的，如A、B、C的使用频率远远高于X、Y、Z，自然会想到设计编码时，让使用频率高的用短码，使用频率低的用长码，以优化整个报文编码。
为使不等长编码为前缀编码(即要求1个字符的编码不能是另1个字符编码的前缀)，可用字符集中的每个字符作为叶子结点生成一棵编码二叉树，为了获得传送报文的最短长度，可将每个字符的出现频率作为字符结点的权值赋予该结点上，求出此树的最小带权路径长度就等于求出了传送报文的最短长度。因此，求传送报文的最短长度问题转化为求由字符集中的所有字符作为叶子结点，由字符出现频率作为其权值所产生的哈夫曼树的问题。利用哈夫曼树来设计二进制的前缀编码，既满足前缀编码的条件，又保证报文编码总长最短。
哈夫曼静态编码：它对需要编码的数据进行两遍扫描：第一遍统计原数据中各字符出现的频率，利用得到的频率值创建哈夫曼树，并必须把树的信息保存起来，即把字符0-255(2^8=256)的频率值以2-4BYTES的长度顺序存储起来，（用4Bytes的长度存储频率值，频率值的表示范围为0--2^32-1，这已足够表示大文件中字符出现的频率了）以便解压时创建同样的哈夫曼树进行解压；第二遍则根据第一遍扫描得到的哈夫曼树进行编码，并把编码后得到的码字存储起来。
哈夫曼动态编码：动态哈夫曼编码使用一棵动态变化的哈夫曼树，对第t+一个字符的编码是根据原始数据中前t个字符得到的哈夫曼树来进行的，编码和解码使用相同的初始哈夫曼树，每处理完1个字符，编码和解码使用相同的方法修改哈夫曼树，所以没有必要为解码而保存哈夫曼树的信息。编码和解码1个字符所需的时间与该字符的编码长度成正比，所以动态哈夫曼编码可实时进行。

哈夫曼译码

在通信中，若将字符用哈夫曼编码形式发送出去，对方接收到编码后，将编码还原成字符的过程，称为哈夫曼译码。

哈夫曼树_哈夫曼树 -程序实现

Basic
VERSION 1.0 CLASS
BEGIN
MultiUse = -1 'True
Persistable = 0 'NotPersistable
DataBindingBehavior = 0 'vbNone
DataSourceBehavior = 0 'vbNone
MTSTransactionMode = 0 'NotAnMTSObject
END
Attribute VB_Name = "clsBinTree"
Attribute VB_GlobalNameSpace = False
Attribute VB_Creatable = True
Attribute VB_PredeclaredId = False
Attribute VB_Exposed = False
Private Type BinTreeType
LChild As Integer
RChild As Integer
Parents As Integer

哈夫曼树Power As Long
End Type
Private BinTree() As BinTreeType
Public UB As Integer
Public Sub InitData(Power As Long, LChild As Integer, RChild As Integer)
If UB = 0 Then UB = 1
ReDim Preserve BinTree(1 To UB)
BinTree(UB).Power = Power
BinTree(UB).LChild = LChild
BinTree(UB).RChild = RChild
UB = UB + 1
End Sub
Private Sub Min(Min1 As Integer, Min2 As Integer, ErrTag As Integer)
Dim P As Integer, Q As Integer
P = 1
While BinTree(P).Parents > 0
P = P + 1
Wend
For I = P + 1 To UB - 1
If BinTree(I).Power < BinTree(P).Power And BinTree(I).Parents = 0 Then P = I
Next
Q = 1
While BinTree(Q).Parents > 0 Or Q = P
Q = Q + 1
If Q = UB Then
ErrTag = 1
Exit Sub
End If
Wend
ForI=Q+1ToUB-1
IfBinTree(I).Power<BinTree(Q).PowerAndQ<>PAndBinTree(I).Parents=0ThenQ=I
Next
Min1=P:Min2=Q:ErrTag=0
EndSub
PublicSubHuffman()
DimErrorHappenAsInteger
DimMin1AsInteger,Min2AsInteger
DimIAsInteger
MinMin1,Min2,ErrorHappen
DoUntilErrorHappen
InitDataBinTree(Min1).Power+BinTree(Min2).Power,Min1,Min2
BinTree(Min1).Parents=UB-1
BinTree(Min2).Parents=UB-1
MinMin1,Min2,ErrorHappen
Loop
EndSub
PublicFunctionHuffmanCode(IAsInteger)AsString
HuffmanCode=I&",LChild:"&BinTree(I).LChild&"RChild:"&BinTree(I).RChild&"Parents:"&BinTree(I).Parents&"Power:"&BinTree(I).Power
EndFunction
AttributeVB_Name="Module1"
PublicHTAsNewclsBinTree
PrivateWordAsString,Ping()AsInteger,PUBAsInteger
PublicSubCreatHT(WordsAsString)
DimTempAsString,IAsInteger
Word=""
ForI=1ToLen(Words)
Temp=Mid(Words,I,1)
P=InStr(1,Word,Temp)
IfP>0Then
Ping(P-1)=Ping(P-1)+1
Else
Word=Word&Temp
ReDimPreservePing(PUB)
Ping(PUB)=1
PUB=PUB+1
EndIf
Next
Form1.Text2.SelText=Word&vbCrLf
ForI=0ToPUB-1
Form1.Text2.SelText=Ping(I)&","
HT.InitD(www.61k.com]ataCLng(Ping(I)),0,0
Next
Form1.Text2.SelText=vbCrLf&vbCrLf
HT.Huffman
ForI=1ToHT.UB-1
Form1.Text2.SelText=HT.HuffmanCode(I)&vbCrLf
Next
EndSub
Pascal

Programhuffman_tree(input,output);
constmax=32767;n=20;m=2*n-1
Typetnode=RECORD
data:integer;
Lc,Rc:integer;
END;
Vartree:ARRAY[0..m]oftnode;
weight:ARRAY[0..n]ofinteger;
im,num:integer;
procedureinitial;
vari:integer;
begin
write('Firstinputnun(<',n:2,')');
readln(num);
writeln('Pleaseinputweight:');
fori:=0tonum-1doread(weight[i])
end;
functionminimum:integer;
vari:integer;
begin
min:=max;
fori:=0tonum-1do
if(min>weight[i])then
begin
min:=weight[i];
im:=i;
end;
weight[im]:=max;
minimum:=min;
end;
procedurehuffman;
vari,k:integer;
begin
fori:=numto2*num-1do
begin
tree[i].Lc:=minimum;
tree[i].Rc:=minimum;
tree[i].data:=tree[i].Lc:+tree[i].Rc;
weight[im]:=tree[i].data
end;
writeln;
writeln('Theresultofhuffmantree:');
k:=1;
fori:=2*num-2downtonumdo
begin
write(tree[i].data:6,':',tree[i].Lc:3,tree[i].Rc:3);
if(kmod3=0)thenwriteln;k:=k+1;
end
writeln
end;
procedureprintd;
vari:integer;
begin
write('Theweightoftree:');
fori:=0tonum-1do
write{weight[i]:3}
end;
begin{main}
initial;
printd;
huffman
end.
C++

#include
#include
usingnamespacestd;
constintMaxValue=10000;//初始设定的权值最大值
constintMaxBit=4;//初始设定的最大编码位数
constintMaxN=10;//初始设定的最大结点个数
structHaffNode//哈夫曼树的结点结构
{
intweight;//权值
intflag;//标记
intparent;//双亲结点下标
intleftChild;//左孩子下标
intrightChild;//右孩子下标
};
structCode//存放哈夫曼编码的数据元素结构
{
intbit[MaxN];//数组
intstart;//编码的起始下标
intweight;//字符的权值
};
voidHaffman(intweight[],intn,HaffNodehaffTree[])
//建立叶结点个数为n权值为weight的哈夫曼树haffTree
{
intj,m1,m2,x1,x2;
//哈夫曼树haffTree初始化。n个叶结点的哈夫曼树共有2n-一个结点
for(inti=0;i<2*n-1;i++)
{
if(i<n)
haffTree[i].weight=weight[i];
elsehaffTree[i].weight=0;
haffTree[i].parent=0;
haffTree[i].flag=0;
haffTree[i].leftChild=-1;
haffTree[i].rightChild=-1;
}
//构造哈夫曼树haffTree的n-一个非叶结点
for(inti=0;i<n-1;i++)
{
m1=m2=MaxValue;
x1=x2=0;
for(j=0;j<n+i;j++)
{
if(haffTree[j].weight<m1&&haffTree[j].flag==0)
{
m2=m1;
x2=x1;
m1=haffTree[j].weight;
x1=j;
}
else
if(haffTree[j].weight<m2&&haffTree[j].flag==0)
{
m2=haffTree[j].weight;
x2=j;
}
}
//将找出的两棵权值最小的子树合并为一棵子树
haffTree[x1].parent=n+i;
haffTree[x2].parent=n+i;
haffTree[x1].flag=1;
haffTree[x2].flag=1;
haffTree[n+i].weight=haffTree[x1].weight+haffTree[x2].weight;
haffTree[n+i].leftChild=x1;
haffTree[n+i].rightChild=x2;
}
}
voidHaffmanCode(HaffNodehaffTree[],intn,CodehaffCode[])
//由n个结点的哈夫曼树haffTree构造哈夫曼编码haffCode
{
Code*cd=newCode;
intchild,parent;
//求n个叶结点的哈夫曼编码
for(inti=0;i<n;i++)
{
cd->start=n-1;//不等长编码的最后一位为n-1
cd->weight=haffTree[i].weight;//取得编码对应权值的字符
child=i;
parent=haffTree[child].parent;
//由叶结点向上直到根结点
while(parent!=0)
{
if(haffTree[parent].leftChild==child)
cd->bit[cd->start]=0;//左孩子结点编码0
else
cd->bit[cd->start]=1;//右孩子结点编码1
cd->start--;
child=parent;
parent=haffTree[child].parent;
}
//保存叶结点的编码和不等长编码的起始位
for(intj=cd->start+1;j<n;j++)
haffCode[i].bit[j]=cd->bit[j];
haffCode[i].start=cd->start;
haffCode[i].weight=cd->weight;//保存编码对应的权值
}
}
intmain()
{
inti,j,n=4;
intweight[]={1,3,5,7};
HaffNode*myHaffTree=newHaffNode[2*n+1];
Code*myHaffCode=newCode[n];
if(n>MaxN)
{
cout<<"定义的n越界，修改MaxN!"<<endl;
exit(0);
}
Haffman(weight,n,myHaffTree);
HaffmanCode(myHaffTree,n,myHaffCode);
//输出每个叶结点的哈夫曼编码
for(i=0;i<n;i++)
{
cout<<"Weight="<<myHaffCode[i].weight<<"Code=";
for(j=myHaffCode[i].start+1;j<n;j++)
cout<<myHaffCode[i].bit[j];
cout<<endl;
}
return0;
}
C

#include
#include
#defineN8
typedefstructnode{
intitem;
structnode*l;
structnode*r;
}*link;
link*h;
intNq=N;
linkNODE(intitem,linkl,linkr)
{
linkt=malloc(sizeof*t);
t->l=l;
t->r=r;
t->item=item;
returnt;
}
voidshif_up(inti)
{
intj;
while(i>1)
{
j=i/2;
if()
}
}
voidinsert(linkt)
{
h[++Nq]=t;
shif_up(Nq);
}
linkdelmin()
{
swap(1,Nq--);
shif_down(1,Nq);
returnh[Nq+1];
}
linkcreat_heap(intfreq,intlen)
{
inti;
for(i=0;i<len;i++)
h[i]=NODE(freq[i],NULL,NULL);
for(i=N/2;i>=0;i--)
shif_down(i,N);}
voidhuffman(intfreq[],intlen)
{
h=malloc(len*sizeof(link));
creat_heap(h,freq,len);
while(Nq>1)
{
linkt1=delmin();
linkt2=delmin();
insert(NODE(t1->item+t2->item,t1,t2));
}
}
intmain(void)
{
intfreq[N]={5,29,7,8,14,23,3,11};
huffman(freq,N);
return0;
}

二 : 哈夫曼树的构造

哈夫曼树的构造

构造哈夫曼树的过程是这样的

一、构成初始集合

对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F={T1,T2,T3,...,Ti,...,Tn}，其中每棵二叉树Ti中只有一个权值为Wi的根结点，它的左右子树均为空。（www.61k.com]（为方便在计算机上实现算法，一般还要求以Ti的权值Wi的升序排列。）

二、选取左右子树

在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，新二叉树的根结点的权值为其左右子树的根结点的权值之和。

三、删除左右子树

从F中删除这两棵树，并把这棵新的二叉树同样以升序排列加入到集合F中。

四、重复二和三两步，

重复二和三两步，直到集合F中只有一棵二叉树为止。

举个例子

有个序列是(7,9,2,6,32,3,21,10)

叫你求哈夫曼树

步骤一：把这些点都看成是一个只有根结点的树的集合F

步骤二，选2个值最小的树

步骤三：在这些树的集合F中删除这2棵树

哈夫曼树 哈夫曼树的构造

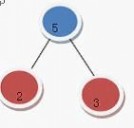
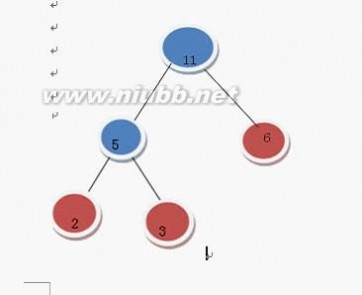
然后把 构成一颗二叉树 变成了（5 = 2 + 3）

然后把这个树加入到集合F

5代表这棵树的权值

然后继续上述步骤

肯定是选 5 和 6

把这2个构成二叉树

在F中删除5 6 加入11这棵树

变成了

哈夫曼树 哈夫曼树的构造

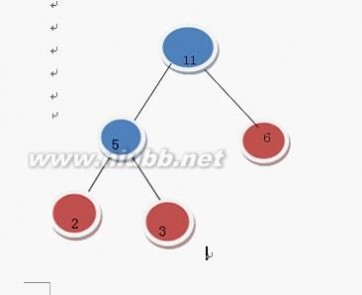
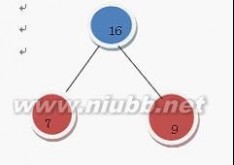
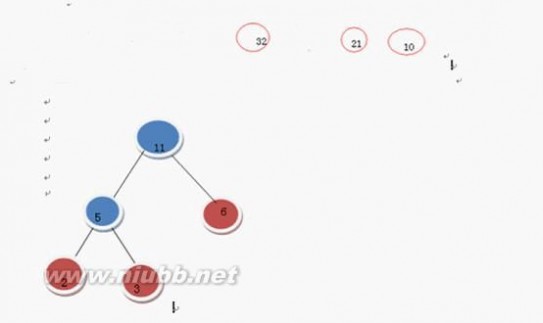
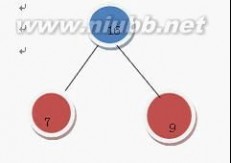
继续上述步骤 选7 和 9

在F中删除7 和9 加入16这棵树 变成了

哈夫曼树 哈夫曼树的构造

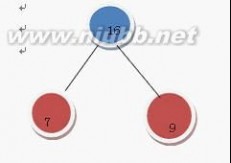
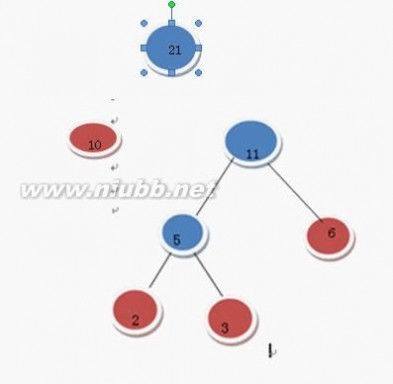
继续上述步骤

选 10 和11

在F中删除10 和11 加入21这棵树

哈夫曼树 哈夫曼树的构造

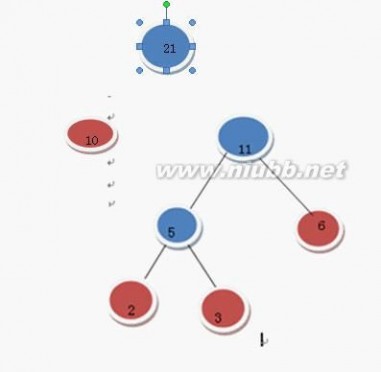
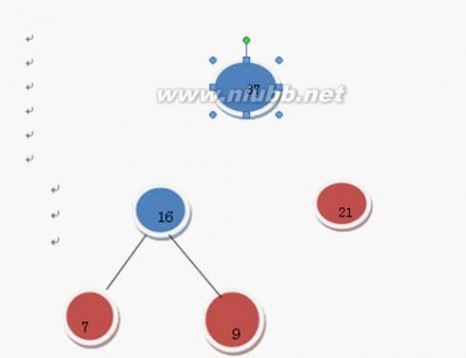
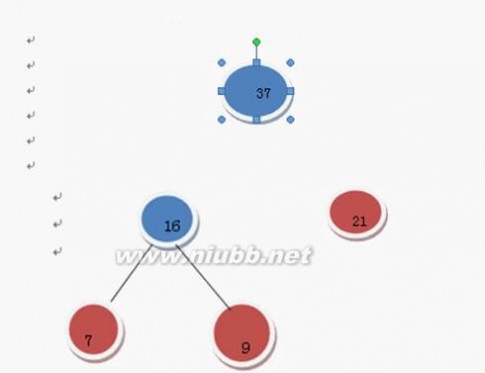
继续上述步骤选16和21 （有2个21，随便选哪个） 我选那个只有一个根结点的21好了 16和21构成二叉树

在F中删除这16和21这两棵树 加入37这棵树

哈夫曼树 哈夫曼树的构造

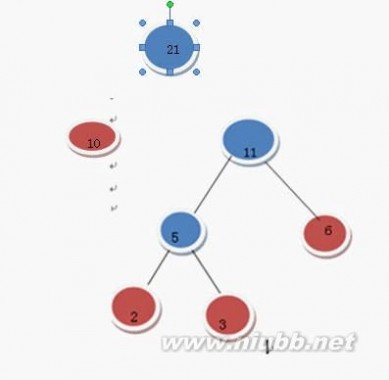
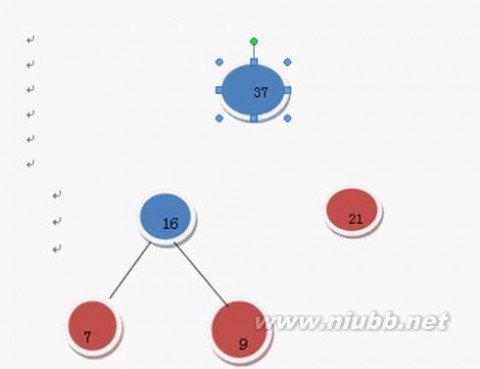
继续上述步骤 选21和32 构成二叉树

哈夫曼树 哈夫曼树的构造

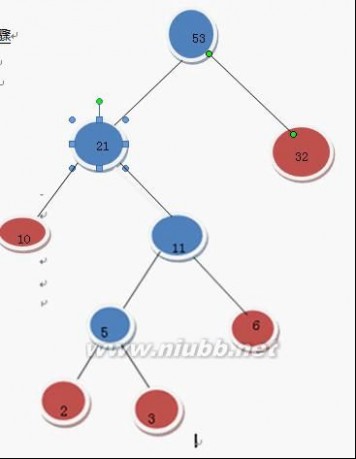
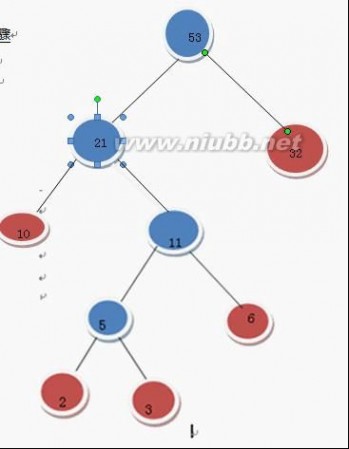
在F中删除21和32这2两棵树 加入53这棵树

哈夫曼树 哈夫曼树的构造

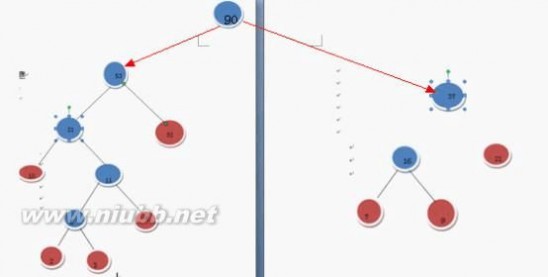
还是继续上面步骤

把F中的两棵树合并成一棵树

完成了!

这个就是哈夫曼树

三 : 哈夫曼树的构造

哈夫曼树的构造

构造哈夫曼树的过程是这样的

一、构成初始集合

对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F={T1,T2,T3,...,Ti,...,Tn}，其中每棵二叉树Ti中只有一个权值为Wi的根结点，它的左右子树均为空。（为方便在计算机上实现算法，一般还要求以Ti的权值Wi的升序排列。）

二、选取左右子树

在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，新二叉树的根结点的权值为其左右子树的根结点的权值之和。

三、删除左右子树

从F中删除这两棵树，并把这棵新的二叉树同样以升序排列加入到集合F中。

四、重复二和三两步，

重复二和三两步，直到集合F中只有一棵二叉树为止。

举个例子

有个序列是(7,9,2,6,32,3,21,10)

叫你求哈夫曼树

步骤一：把这些点都看成是一个只有根结点的树的集合F

步骤二，选2个值最小的树

步骤三：在这些树的集合F中删除这2棵树

然后把 构成一颗二叉树 变成了（5 = 2 + 3）

然后把这个树加入到集合F

5代表这棵树的权值

然后继续上述步骤

肯定是选 5 和 6

把这2个构成二叉树

在F中删除5 6 加入11这棵树

变成了

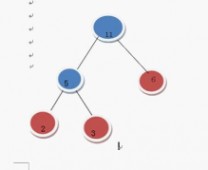
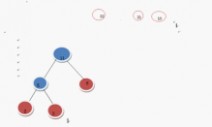
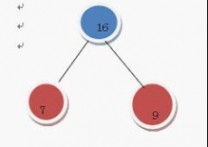
继续上述步骤 选7 和 9

在F中删除7 和9 加入16这棵树 变成了

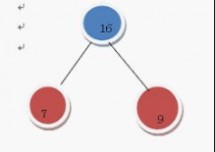
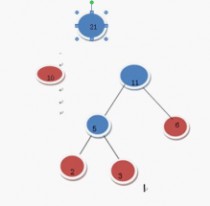
继续上述步骤

选 10 和11

在F中删除10 和11 加入21这棵树

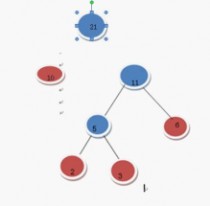
继续上述步骤选16和21 （有2个21，随便选哪个） 我选那个只有一个根结点的21好了 16和21构成二叉树

在F中删除这16和21这两棵树 加入37这棵树

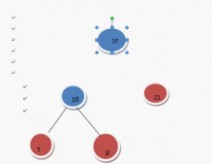
继续上述步骤 选21和32 构成二叉树

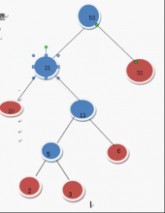
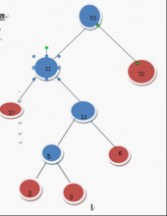
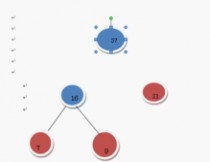
在F中删除21和32这2两棵树 加入53这棵树

还是继续上面步骤

把F中的两棵树合并成一棵树

完成了!

这个就是哈夫曼树

四 : 数据结构哈夫曼树的应用

一、实验名称

数据结构哈夫曼树的应用

二、问题描述

利用赫夫曼编码进行通信可以大大提高信道利用率，缩短信息传输时间，降低传输成本。这要求在发送端通过一个编码系统对待传输数据预先编码，在接收端将传来的数据进行译码（复原）。对于双工信道（即可以双向传输信息的信道），每端都需要一个完整的编/译码系统。试为这样的信息收发站编写一个赫夫曼码的编/译码系统。

三、基本要求

一个完整的系统应具有以下功能：

(1)I：初始化（Initialization）。从终端读入字符集大小n，以及n个字符和n个权值，建立赫夫曼树，并将它存于文件hfmTree中。

(2)E：编码（Encoding）。利用已建好的赫夫曼树（如不在内存，则从文件hfmTree中读入），对文件ToBeTran中的正文进行编码，然后将结果存入文件CodeFile中。

(3)D：译码（Decoding）。利用已建好的赫夫曼树将文件CodeFile中的代码进行译码，结果存入文件Textfile中。

以下为选作：

(4)P：印代码文件（Print）。将文件CodeFile以紧凑格式显示在终端上，每行50个代码。同时将此字符形式的编码文件写入文件CodePrin中。

(5)T：印赫夫曼树（Treeprinting）。将已在内存中的赫夫曼树以直观的方式（比如树）显示在终端上，同时将此字符形式的赫夫曼树写入文件TreePrint中。

四、测试要求

(1)已知某系统在通信联络中只可能出现八种字符，其频率分别为0.05,0.29,0.07,0.08,0.14,0.23,0.03,0.11，试设计赫夫曼编码。

(2)用下表给出的字符集和频度的实际统计数据建立赫夫曼树，并实现以下报文的编码和译码：“THISPROGRAMEISMYFAVORITE”。

字符		A	B	C	D	E	F	G	H	I	J	K	L	M
频度	186	64	13	22	32	103	21	15	47	57	1	5	32	20
字符	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
频度	57	63	15	1	48	51	80	23	8	18	1	16	1

(3)编码结果以文本方式存储在文件Codefile中。

(4)用户界面可以设计为“菜单”方式：显示上述功能符号，再加上“Q”，表示退出运行Quit。请用户键入一个选择功能符。此功能执行完毕后再显示此菜单，直至某次用户选择了“Q”为止。

(5)在程序的一次执行过程中，第一次执行I，D或C命令之后，赫夫曼树已经在内存了，不必再读入。每次执行中不一定执行I命令，因为文件hfmTree可能早已建好。

五、源代码/数据测试

#include<iostream.h>

#include<stdio.h>

#include<stdlib.h>

#include<string.h>

#include<fstream.h>

typedefstruct{//赫夫曼树的结构体

charch;

intweight;//权值

intparent,lchild,rchild;

}htnode,*hfmtree;

typedefchar**hfmcode;

voidSelect(hfmtree&HT,inta,int*p1,int*p2)//Select函数，选出HT树到a为止，权值最小且parent为0的2个节点

{

inti,j,x,y;

for(j=1;j<=a;++j){

if(HT[j].parent==0){

x=j;

break;

}

}

for(i=j+1;i<=a;++i){

if(HT[i].weight<HT[x].weight&&HT[i].parent==0){

x=i;//选出最小的节点

}

}

for(j=1;j<=a;++j) {

if(HT[j].parent==0&&x!=j)

{

y=j;

break;

}

}

for(i=j+1;i<=a;++i)

{

if(HT[i].weight<HT[y].weight&&HT[i].parent==0&&x!=i)

{

y=i;//选出次小的节点

}

}

if(x>y){

*p1=y;

*p2=x;

}

else

{

*p1=x;

*p2=y;

}

}

voidhfmcoding(hfmtree&HT,hfmcode&HC,intn)//构建赫夫曼树HT，并求出n个字符的赫夫曼编码HC

{

inti,start,c,f,m,w;

intp1,p2;

char*cd,z;

if(n<=1){

return;

}

m=2*n-1;

HT=(hfmtree)malloc((m+1)*sizeof(htnode));

for(i=1;i<=n;++i)//初始化n个叶子结点

{

printf("请输入第%d字符信息和权值：",i);

scanf("%c%d",&z,&w);

while(getchar()!='n')

{

continue;

}

HT[i].ch=z;

HT[i].weight=w;

HT[i].parent=0;

HT[i].lchild=0;

HT[i].rchild=0;

}

for(;i<=m;++i)//初始化其余的结点

{

HT[i].ch='0';

HT[i].weight=0;

HT[i].parent=0;

HT[i].lchild=0;

HT[i].rchild=0;

}

for(i=n+1;i<=m;++i)//建立赫夫曼树

{

Select(HT,i-1,&p1,&p2);

HT[p1].parent=i;HT[p2].parent=i;

HT[i].lchild=p1;HT[i].rchild=p2;

HT[i].weight=HT[p1].weight+HT[p2].weight;

}

HC=(hfmcode)malloc((n+1)*sizeof(char*));

cd=(char*)malloc(n*sizeof(char));

cd[n-1]='';

for(i=1;i<=n;++i)//给n个字符编码

{

start=n-1;

for(c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent)

{

if(HT[f].lchild==c)

{

cd[--start]='0';

}

else

{

cd[--start]='1';

}

}

HC[i]=(char*)malloc((n-start)*sizeof(char));

strcpy(HC[i],&cd[start]);

}

free(cd);

}

intmain(){

charcode[100],h[100],hl[100];

intn,i,j,k,l;

ifstreaminput_file;//文件输入输出流

ofstreamoutput_file;

charchoice,str[100];

hfmtreeHT;

hfmcodeHC;

cout<<"n";

cout<<""<<"计算机（3）班"<<""<<"n";

while(choice!='Q'&&choice!='q')//当choice的值不为q且不为Q时循环

{

cout<<""<<"*************************赫夫曼编码/译码器*************************n";

cout<<""<<"I.Init"<<""<<"E.Encoding"<<""<<"D.Decoding"<<""<<"Q.Exitn";

cout<<"请输入您要操作的步骤：";

cin>>choice;

if(choice=='I'||choice=='i')//初始化赫夫曼树

{

cout<<"请输入字符个数：";

cin>>n;

hfmcoding(HT,HC,n);

for(i=1;i<=n;++i)

{

cout<<HT[i].ch<<":"<<HC[i]<<endl;

}

output_file.open("hfmTree.txt");

if(!output_file){

cout<<"can'toenfile!"<<endl;

return1;

}

for(i=1;i<=n;i++)

{

output_file<<"("<<HT[i].ch<<HC[i]<<")";

}

output_file.close();

cout<<"赫夫曼树已经创建完毕，并且已经放入hfmTree.txt文件中!"<<endl;

}

elseif(choice=='E'||choice=='e')//进行编码，并将字符放入ToBeTran.txt，码值放入CodeFile.txt中

{

printf("请输入字符：");

gets(str);

output_file.open("ToBeTran.txt");

if(!output_file)

{

cout<<"can'topenfile!"<<endl;

return1;

}

output_file<<str<<endl;

output_file.close();

output_file.open("CodeFile.txt");

if(!output_file){

cout<<"can'toenfile!"<<endl;

return1;

}

for(i=0;i<strlen(str);i++){

for(j=0;j<=n;++j)

{

if(HT[j].ch==str[i])

{

output_file<<HC[j];

break;

}

}

}

output_file.close();

cout<<"n";

cout<<"编码完毕，并且已经存入CodeFile.txt文件！n";

input_file.open("CodeFile.txt");//从CodeFile.txt中读入编码，输出在终端

if(!input_file)

{

cout<<"can'toenfile!"<<endl;

return1;

}

input_file>>code;

cout<<"编码码值为："<<code<<endl;

input_file.close();

}

elseif(choice=='D'||choice=='d')//读入CodeFile.txt中的编码进行译码，将译出来的字符放入Textfile.txt中

{

input_file.open("CodeFile.txt");

if(!input_file){

cout<<"can'toenfile!"<<endl;

return1;

}

input_file>>h;

input_file.close();

output_file.open("Textfile.txt");

if(!output_file)

{

cout<<"can'toenfile!"<<endl;

return1;

}

k=0;

while(h[k]!='')//先用编码中的前几个和字符的编码相比较，然后往后移

{

for(i=1;i<=n;i++){

l=k;

for(j=0;j<strlen(HC[i]);j++,l++){

hl[j]=h[l];

}

hl[j]='';

if(strcmp(HC[i],hl)==0)

{

output_file<<HT[i].ch;

k=k+strlen(HC[i]);

break;

}

}

}

output_file.close();

input_file.open("Textfile.txt");

if(!input_file){

cout<<"can'toenfile!"<<endl;

return1;

}

input_file>>h;

cout<<h<<endl;

input_file.close();

cout<<"译码结束，字符已经存入Textfile.txt文件中！"<<endl;

}

elseif(choice=='Q'||choice=='q')//退出程序

{

exit(0);

}

else//如果选了选项之外的就让用户重新选择

{

cout<<"您没有输入正确的步骤，请重新输入！"<<endl;

}

cout<<endl;

}

return0;

}

六、测试情况

编码译码

数据存储情况

本文标题：哈夫曼树的构造-哈夫曼树：哈夫曼树-基本术语，哈夫曼树-结构构造
本文地址： http://www.61k.com/1128243.html