一 : 采用matlab求解矩阵的逆的方法

对于学习matlab矩阵的新手，求逆是一个个很重的过程。矩阵的逆，在数学的应用领域是一个很重的运算。今天小编将为大家带来的是采用matlab求解矩阵的逆的方法；一起去看看吧！

软件名称：

数学软件Matlab R2015b 32位 完全破解版(附破解文件+密钥+安装教程)

软件大小：

6.75GB

更新时间：

2016-11-23

软件名称：

数学软件Matlab R2016a 64位 完全破解版(附破解文件+密钥+安装教程)

软件大小：

7.6GB

更新时间：

2016-11-23

方法：

1、打开matlab软件；

2、输入一下代码，清屏和工作空间；

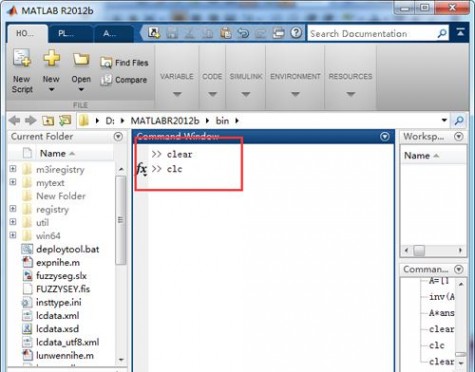
3、输入自己的矩阵，如本例中设置一个矩阵A=[1 2 ;3 4 ];

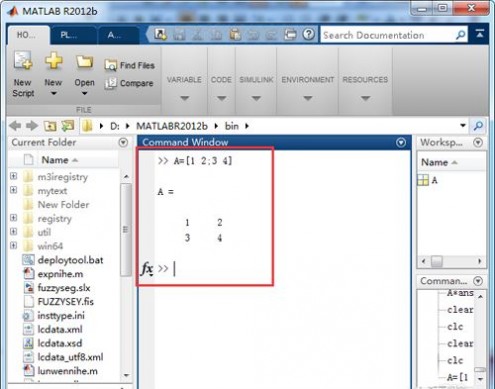
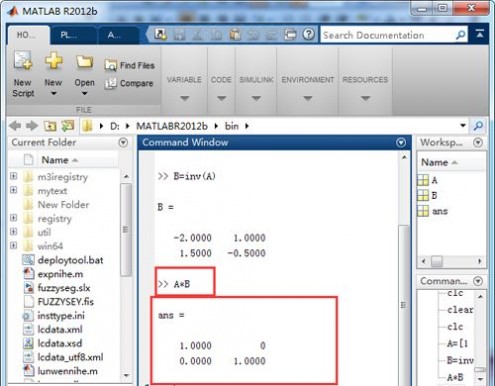
4、输入求解矩阵逆的程序，如图所示；

B=inv(A)

5、验证自己求解的逆，两个矩阵的乘积为单位阵，求逆正确；

二 : 伴随矩阵法求逆矩阵2008

伴随矩阵法求逆矩阵

1

一、方阵的行列式
定理 设A、B 为 n 阶方阵，那么 AB ? A B . 很明显 AB ? A B ? B A ? BA 推论 设 A1 , A2 ,?, An 都为 n 阶方阵，那么

A1 A2 ? An ? A1 A2 ? An .

2

二、伴随矩阵与逆矩阵
定义 行列式 A 的各个元素的代数余子式Aij 所 构成的如下矩阵

? A11 ? ? A12 ? A ?? ? ? ?A ? 1n

A21 A22 ? A2 n

? An1 ? ? ? An 2 ? ? ?? ? ? Ann ? ?

称为矩阵 A 的伴随矩阵.
3

性质 证明

AA? ? A? A ? A E .

? a11 a12 ? a1n ? ? A11 A21 ? An1 ? ? ?? ? a21 a ? ? 12 ? ? A? n A ? A ?a11 A1122 a12 Aa2 n? ?12 a1A22 1n? An 2 ? AA? ? ? a11 A12 ? a12 A22 ? ? ? a1n A2 n ? 0 ? ?? ? ? ? ? ? ? ? ? a? 1 An1 ? an 2 An 2 ? ? ? ? ann Ann ? A ? ? n ?a a ? a ? ? A A ? A ? ? n1 n 2 nn ? ? 1n 2n nn ?
? A ? ? ?? ? ? ? A

O

?

O
A

故
4

AA? ? A E

? ? ? ?, ? A? ?

? 同理可得 AA ? A E

定理1

矩阵 A 可逆的充要条件是 A ? 0 ，且 1 ? ?1 A ? A, A

其中A?为矩阵A的伴随矩阵.

5

证明 若 A 可逆， 即有A?1使AA ?1 ? E .

故 A ? A?1 ? E ? 1,

所以 A ? 0.

当 A ? 0时,

A? A? AA? ? A? A ? A E ? A ? A ? E , A A
按逆矩阵的定义得

A A ? . A
?1

?

证毕

6

奇异矩阵与非奇异矩阵的定义
当 A ? 0时, A称为奇异矩阵, 当 A ? 0时, A称为非奇异矩阵 .

由此可得 是可逆阵的充要条件是 A A为 非奇异矩阵 .

7

n 推论1 设A是n阶方阵，如果存在 阶方阵B， 使AB ? E ?或BA ? E ?，则B ? A?1 .
A ? B ? E ? 1,

证明

故 A ? 0,

因而A?1存在, 于是
B ? EB ? A?1 A B ? A?1 ? AB?

?

?

?A E ?A
?1

?1

证毕

8

推论2 若A可逆, 则有 A
证明

?1

? A .

?1

? AA ?1 ? E ? A A ?1 ? 1

因此 A ? A .
?1

?1

推论3 设 A、B 为 n 阶方阵，若 A 不可逆， 那么 AB、BA都不可逆.
证明
因为A不可逆， 故 A ? 0,

因此 AB ? A B ? 0.
所以AB也不可逆.
9

例 下列矩阵A, B是否可逆? 若可逆，用伴随矩阵
法求逆矩阵.

? 1 2 3? ? ? A ? ? 2 1 2 ?, ? 1 3 3? ? ?

? 2 3 ?1 ? ? ? B ? ??1 3 5 ?. ? 1 5 ? 11? ? ?

1 2 3
解

A ? 2 1 2 ? 4 ? 0, 所以A可逆 . 1 3 3

10

?1 2 ? A ? ?2 1 ?1 3 ? 1 2 A11 ? ? ?3, 3 3

3? ? 2 ?, 3? ?

A ? 4,

2 2 2 1 A12 ? ? ? ?4, A13 ? ? ? 5, 1 3 1 3

2 3 1 3 1 2 A21 ? ? ? 3, A22 ? ? 0, A23 ? ? ? ?1, 3 3 1 3 1 3 1 3 1 2 A31 ? ? 1, A32 ? ? ? 4, A33 ? ? ?3, 2 2 2 1 1 2
1 ? ?? 3 3 ? 1 * 1? ?1 ?A ? A ? ??4 0 4 ?. A 4? 11 5 ? 1 ? 3? ? ?

2 3

? 2 3 ?1 ? ? ? B ? ??1 3 5 ?. ? 1 5 ? 11 ? ? ?
2 1 3 ?

1 5
? 0, 故B不可逆 .

由于 B ? ? 1 3

5 ? 11

12

1 , , det 例: 设A为n阶 方 阵 A 为 其 伴 随 矩 阵 A ? , 3 ? ? 1 ? ?1 ? ?? 求 det? ? A ? ? 15 A . ?? 4 ? ? ? ? 1 解: 由于 A ? , 故 A 可逆， 3 1 ?1 ? ? ?1 又由 AA ? A E , 可知 A ? A A ? A , 3 ?1 ?? 1 ? ? ?? 故 det? ? A ? ? 15 A ? det? 4 A?1 ? 15 ? 1 A?1 ? ? ? ?? 4 ? ? 3 ? ? ? ? n 1 n ?1 ?1 ? (?1)n ? 3 ? ( ?1) A ? (?1) ? det?? A ? A
?

13

Crame法则

1

一、克拉默法则（定理） 如果线性方程组
? a11 x1 ? a12 x 2 ? ? ? a1n x n ? b1 ?a x ? a x ? ? ? a x ? b ? 21 1 22 2 2n n 2 ? ? ???????????? ?a n1 x1 ? a n 2 x 2 ? ? ? a nn x n ? bn ?

(1)

a11 a12 ? a1 n a 21 a 22 ? a 2 n ?0 的系数行列式不等于零，即D ? ??????? a n1 a n 2 ? a nn
2

那么线性方程组?1? 有解，并且解是唯一的，解 可以表为

Dn D1 D2 D2 x1 ? , x2 ? , x3 ? ,? , xn ? . D D D D
其中 D j 是把系数行列式 D 中第 j 列的元素用方程 组右端的常数项代替后所得到的 n 阶行列式，即

a11 ? a1 , j ?1 b1 a1 , j ?1 ? a1 n D j ? ??????????? a n 1 ? a n , j ?1
3

bn

a n , j ?1 ? a nn

例1 用克拉默则解方程组

? 2 x1 ? x2 ? 5 x3 ? x4 ? 8, ? x ? 3 x ? 6 x ? 9, ? 1 2 4 ? ? 2 x2 ? x3 ? 2 x4 ? ?5, ? x1 ? 4 x2 ? 7 x3 ? 6 x4 ? 0. ?
解

2

1

?5

1
r1 ? 2r2
r4 ? r2

0

7

?5

13

1 ?3 0 ?6 D? 0 2 ?1 2 1 4 ?7 6
7

1 ?3 0 ?6 0 2 ?1 2 0 7 ? 7 12

7 ? 5 13 ? ?2 ?1 2 7 ? 7 12

c1 ? 2c2

?3 ?5

3

c3 ? 2c2

? 0 ?1 0 ?7 ?7 ?2

?

?3
8

3

?7 ?2

? 27,
?5 1 2 8 ?5 1 1 9 0 ?6 D2 ? 0 ? 5 ?1 2 1 0 ?7 6

1

9 ?3 0 ?6 D1 ? ? 5 2 ?1 2 0 4 ?7 6

? 81,
8

? ?108,

2

1

8

1

2

1

?5

8

1 ?3 9 ?6 D3 ? 0 2 ?5 2 1 4 0 6

1 ?3 0 9 D4 ? 0 2 ?1 ? 5 1 4 ?7 0

? ?27,
D1 81 ? x1 ? ? ? 3, D 27
D3 ? 27 x3 ? ? ? ?1, D 27
9

? 27,
D2 ? 108 x2 ? ? ? ?4, D 27
D4 27 x4 ? ? ? 1. D 27

二、重要定理
? a11 x1 ? a12 x 2 ? ? ? a1n x n ? b1 ?a x ? a x ? ? ? a x ? b ? 21 1 22 2 2n n 2 ? ? ???????????? ?a n1 x1 ? a n 2 x 2 ? ? ? a nn x n ? bn ?

(1)

定理1 如果线性方程组?1?的系数行列式 D ? 0, 则 ?1?一定有解,且解是唯一的 . 定理2 如果线性方程组 ?1? 无解或有两个不同的 解，则它的系数行列式必为零.

10

齐次线性方程组的相关定理

? a11 x1 ? a12 x 2 ? ? ? a1 n x n ? 0 ?a x ? a x ? ?? a x ? 0 ? 21 1 22 2 2n n ? ????????????? ?a n1 x1 ? a n 2 x 2 ? ? ? a nn x n ? 0 ?
定理 定理

?2 ?

如果齐次线性方程组 ?2? 的系数行列式 D ? 0 则齐次线性方程组 ?2? 只有零解. 如果齐次线性方程组 ?2? 有非零解,则它

的系数行列式必为零.
11

以上两个定理说明系数行列式 D ? 0 是齐次线性方程组有非零解的必要条件，事
实上，这一条件也是充分的 即系数行列式 D ? 0

? a11 x1 ? a12 x2 ? ? ? a1n xn ? 0 ?a x ? a x ? ?? a x ? 0 ? 21 1 22 2 2n n ? ? ?????????? ? ?? ?an1 x1 ? an 2 x2 ? ? ? ann xn ? 0 ?
有非零解.

这一结论已在Ch2中证明过.
12

例2 问 ? 取何值时，齐次方程组
??1 ? ? ? x1 ? 2 x2 ? 4 x3 ? 0, ? ? 2 x1 ? ?3 ? ? ? x2 ? x3 ? 0, ? x ? x ? ?1 ? ? ? x ? 0, ? 1 2 3

有非零解？

13

解
1? ? D? 2 1
3

?2 3?? 1

4 1 1? ?

1? ? ? 2 1

?3?? 1? ? 0

4 1 1? ?

? ?1 ? ? ? ? ?? ? 3 ? ? 4?1 ? ? ? ? 2?1 ? ? ??? 3 ? ? ? ? ?1 ? ? ? ? 2?1 ? ? ? ? ? ? 3
3 2

? ? (? ? 2)(? ? 3)
齐次方程组有非零解，则 D ? 0 所以 ? ? 0 , ? ? 2 或 ? ? 3时齐次方程组有非零解.
14

三 : 矩阵求导计算法则例题

求导公式(撇号为转置）：

Y = A * X --> DY/DX = A'
Y = X * A --> DY/DX = A
Y = A' * X * B --> DY/DX = A * B'
Y = A' * X' * B --> DY/DX = B * A'

乘积的导数

d(f*g)/dx=(df'/dx)g+(dg/dx)f'

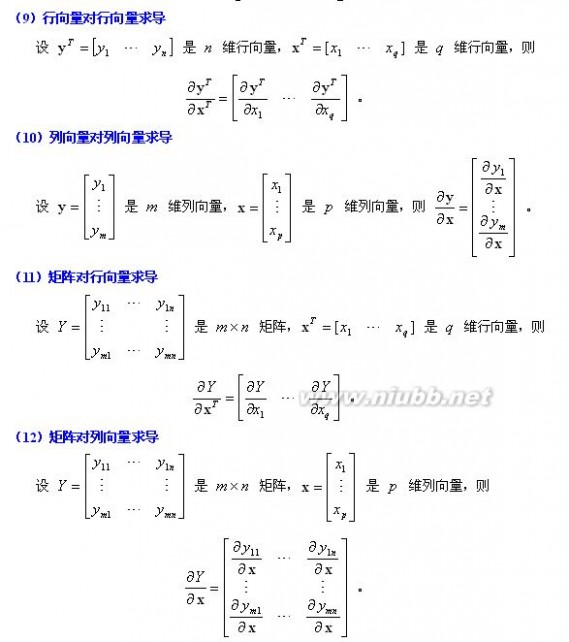
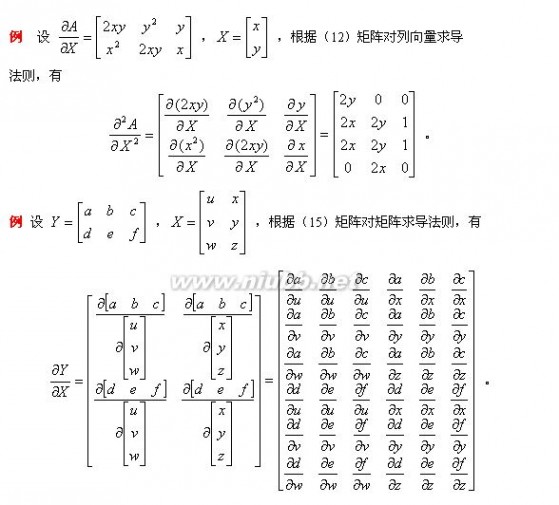
于是把以前学过的矩阵求导部分整理一下：

1. 矩阵Y对标量x求导：

相当于每个元素求导数后转置一下，注意M×N矩阵求导后变成N×M了

Y = [y(ij)]--> dY/dx= [dy(ji)/dx]

2. 标量y对列向量X求导：

注意与上面不同，这次括号内是求偏导，不转置，对N×1向量求导后还是N×1向量

y = f(x1,x2,..,xn)--> dy/dX= (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)'

3. 行向量Y'对列向量X求导：

注意1×M向量对N×1向量求导后是N×M矩阵。

将Y的每一列对X求偏导，将各列构成一个矩阵。

重要结论：

dX'/dX =I

d(AX)'/dX =A'

4. 列向量Y对行向量X’求导：

转化为行向量Y’对列向量X的导数，然后转置。

注意M×1向量对1×N向量求导结果为M×N矩阵。

dY/dX' =(dY'/dX)'

5. 向量积对列向量X求导运算法则：

注意与标量求导有点不同。

d(UV')/dX =(dU/dX)V' + U(dV'/dX)

d(U'V)/dX =(dU'/dX)V +(dV'/dX)U'

重要结论：

d(X'A)/dX =(dX'/dX)A + (dA/dX)X' =IA + 0X' = A

d(AX)/dX' =(d(X'A')/dX)' = (A')' =A

d(X'AX)/dX =(dX'/dX)AX +(d(AX)'/dX)X = AX + A'X

6. 矩阵Y对列向量X求导：

将Y对X的每一个分量求偏导，构成一个超向量。

注意该向量的每一个元素都是一个矩阵。

7. 矩阵积对列向量求导法则：

d(uV)/dX =(du/dX)V + u(dV/dX)

d(UV)/dX =(dU/dX)V + U(dV/dX)

重要结论：

d(X'A)/dX =(dX'/dX)A +X'(dA/dX) = IA + X'0 = A

8. 标量y对矩阵X的导数：

类似标量y对列向量X的导数，

把y对每个X的元素求偏导，不用转置。

dy/dX = [Dy/Dx(ij) ]

重要结论：

y = U'XV=ΣΣu(i)x(ij)v(j) 于是 dy/dX = [u(i)v(j)] =UV'

y = U'X'XU 则dy/dX = 2XUU'

y =(XU-V)'(XU-V) 则 dy/dX = d(U'X'XU- 2V'XU + V'V)/dX = 2XUU' - 2VU' +0 = 2(XU-V)U'

9. 矩阵Y对矩阵X的导数：

将Y的每个元素对X求导，然后排在一起形成超级矩阵。

10.乘积的导数

d(f*g)/dx=(df'/dx)g+(dg/dx)f'

结论

d(x'Ax)=(d(x'')/dx)Ax+(d(Ax)/dx)(x'')=Ax+A'x（注意：''是表示两次转置）

矩阵求导 属于 矩阵计算，应该查找 Matrix Calculus 的文献：

#Intro

http://www.stanford.edu/~dattorro/matrixcalc.pdf

http://www.colorado.edu/engineering/CAS/courses.d/IFEM.d/IFEM.AppD.d/IFEM.AppD.pdf

http://www4.ncsu.edu/~pfackler/MatCalc.pdf

http://center.uvt.nl/staff/magnus/wip12.pdf

本文标题：矩阵求伪逆的算法-采用matlab求解矩阵的逆的方法
本文地址： http://www.61k.com/1123286.html