一 : 试为下面的文法构造一个递归下降的分析程序.产生式为:

试为下面的文法构造一个递归下降的分析程序.产生式为:
bexpr→bterm {or bterm }
bterm→bfactor {and bfactor}
bfactor→not bfactor | (bexpr) | true |false
504的吧
这作业什么时候交啊,是18周吗?
写好了发给我一份啊
让我参考参考

二 : 递归下降分析程序构造
完成以下描述算术表达式的LL(1)文法的递归下降分析程序构造
G[E]:
E→TE′
E′→+TE′|ε
T→FT′
T′→*FT′|ε
F→(E)|i
说明:终结符号i为用户定义的简单变量,即标识符的定义。
要求具有如下功能:
1)从文件读入算术表达式/或者从终端输入
2)总控函数分析算术表达式;
3)根据分析结果正误,分别给出不同信息
通过设计、编制、调试一个递归下降语法分析程序,实现对词法分析程序所提供的单词序列进行语法检查和结构分析,掌握常用的语法分析方法。通过本实验,应达到以下目标:(1) 掌握从源程序文件中读取有效字符的方法和产生源程序的内部表示文件的方法。
(2)、掌握语法分析的实现方法。
(3)、上机调试编出的语法分析程序。
2学时
递归下降法是语法分析中最易懂的一种方法。它的主要原理是,对每个非终结符按其产生式结构构造相应语法分析子程序,其中终结符产生匹配命令,而非终结符则产生过程调用命令。因为文法递归相应子程序也递归,所以称这种方法为递归子程序下降法或递归下降法。其中子程序的结构与产生式结构几乎是一致的。
递归下降分析程序的实现思想是:识别程序由一组子程序组成。每个子程序对应于一个非终结符号。
每一个子程序的功能是:选择正确的右部,扫描完相应的字。在右部中有非终结符号时,调用该非终结符号对应的子程序来完成。
自上向下分析过程中,如果带回溯,则分析过程是穷举所有可能的推导,看是否能推导出待检查的符号串。分析速度慢。而无回溯的自上向下分析技术,可根据输入串的当前符号以及各产生式右部首符,选择某非终结符的产生式,效率高,且不易出错。
无回溯的自上向下分析技术可用的先决条件是:无左递归和无回溯。即:假设A的全部产生式为Aàα1|α2|……|αn,则必须满足如下条件才能保证可以唯一的选择合适的产生式
First(Aàαi)∩First(Aàαj)=Φ,当i≠j.
无左递归:既没有直接左递归,也没有间接左递归。
无回溯:对于人以非中介符号U的产生式右部 ,其对应的字的首终结符号两两不相交。
如果一个文法不含回路(形如 的推导),也不含以 为右部的产生式,那么可以通过执行消除左递归的算法消除文法的一切左递归。
1.根据First集合的定义求文法中每个产生式的First集合,判断是否满足递归下降法分析条件,若不满足用消除左递归和消除公共前缀等文法等价变化算法对文法进行变换,使其满足递归下降法的要求。
2. 构造递归下降语法分析程序
采用递归子程序方法进行语法分析,对文法中的每个非终结符号按其产生式结构产生相应的语法分析子程序,完成相应的识别任务。其中终结符产生匹配命令,非终结符则产生调用命令。每次进入子程序之前都预先读入一个单词。因为使用了递归下降方法,所以程序结构和层次清晰明了,易于手工实现,且时空效率较高。实际的语法分析工作,从调用总程序的分析子程序开始,根据产生式进行递归调用各个分析子程序。
实验目的原理:只是单纯地分析文法,递归地遍历右部分过程,有两个程序,一个是根据非终结符的FIRST集合来编写,另一个则是直接很据非终结符做的,无需计算first集合。关键的地方是要判断输入的字符串最后一个字符为‘\0’..
程序如下:
#include "Stdio.h"
#include "stdlib.h"
#include "string.h"
int i=0;char *s;
void error()
{
printf("error\n");
}
void match(char t)
{
if (s[i] == t)
i++;
else
error();
}
void E()
{
if ((s[i] == '(') || (s[i] == 'i'))
{
printf("E->TE'\n");
T();
E1();
}
else
error();
}
int E1()
{
if(s[i]=='+')
{
printf("E'->+TE'\n");
match('+');
T();
E1();
}
else if ((s[i] == '(') || (s[i] == 'i') || (s[i] == '*') || (s[i]== '\0') || (s[i] == ')'))
printf("E'->&\n");
else
error();
return 0;
}
int T()
{
if ((s[i] == '(') || (s[i] == 'i'))
{
printf( "T->FT'\n");
F();
T1();
}
else
error();
return 0;
}
int T1()
{
if (s[i] == '*')
{
printf( "T'->*FT'\n");
match('*');
F();
T1();
}
else if ((s[i] == '(') || (s[i] == 'i') || (s[i] == '+') || (s[i]== '\0') || (s[i] == ')'))
printf("T'->&\n");
else
error();
return 0;
}
int F()
{
if (s[i] == '(')
{
printf("F->(E)\n");
match('(');
E();
match(')');
}
else if (s[i] == 'i')
{
printf("F->i\n");
match('i');
}
else
error();
return 0;
}
void main()
{
gets(s);
E();
getch();
}
输入结果显示:
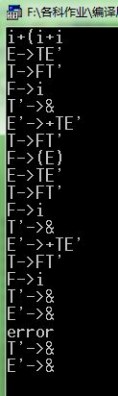
这是根据first集合来做的,自顶向下分析文法。
#include "stdlib.h"
#include "stdio.h"
#include "string.h"
int i=0,flag=1;
char *s;
int E()
{
if(T())
{
if (E_prime())
{
printf("E->TE'\n");
return 1;
}
}
printf("error_%d\n",i);
flag=0;
return 0;
}
int E_prime()
{
if(A())
{
if (T())
{
if (E_prime())
{
printf("E'->ATE'\n");
return 1;
}
else {printf("error_%d\n",i); flag=0;return 0;}
}
else {printf("error_%d\n",i); flag=0;return 0;}
}
return1;
}
int T()
{
if (F())
{
if (T_prime())
{
printf("T->FT'\n");
return 1;
}
}
flag=0;
printf("error_%d\n",i);
return 0;
}
int T_prime()
{
if (M())
{
if (F())
{
if (T_prime())
{
printf("T'->MFT'\n");
return 1;
}
else {printf("error_%d\n",i);flag=0;return 0;}
}
else {printf("error_%d\n",i); flag=0;return 0;}
}
return 1;
}
int F()
{
if (s[i] == '(')
{
advance();
if (E())
{
if (s[i] == ')')
{
advance();
printf("F->(E)\n");
return 1;
}
}
}
else if (s[i] == 'i')
{
advance();
printf("F->i\n");
return 1;
}
flag=0;
printf("error_%d\n",i);
return 0;
}
int A()
{
if (s[i] == '+')
{
advance();
printf("A->+\n");
return 1;
}
else if (s[i] == '-')
{
advance();
printf("A->-\n");
return 1;
}
return 0;
}
int M()
{
if (s[i] == '*')
{
advance();
printf("M->*\n");
return 1;
}
else if (s[i] == '/')
{
advance();
printf("M->/\n");
return 1;
}
return 0;
}
int advance()
{
i=i+1;
return0;
}
int main()
{
gets(s);
E();
if(flag==0)
printf("is error!");
else
printf("is ok!");
getch();
return0;
}
结果如下图:
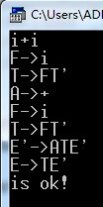

结果是从下至上的分析。。出错时会提示具体错误的位置。。。
三 : 递归下降分析法
编译原理 课程实验报告
班级学号: 姓名:
实验名称: 递归下降分析法
一、实验目的:
根据某一文法编制调试递归下降分析程序,以便对任意输入的符号串进行分析。[www.61k.com)本次实验的目的主要是加深对递归下降分析法的理解。
二、实验要求:
对下列文法,用递归下降分析法对任意输入的符号串进行分析:
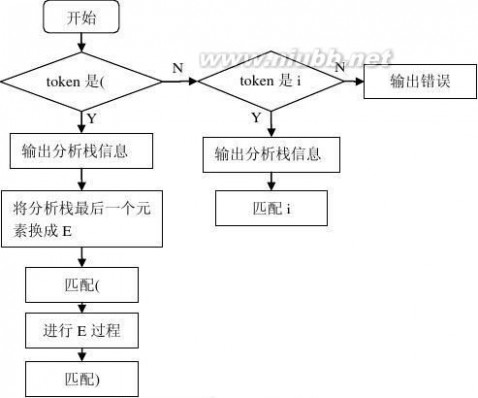
(1)E->TG
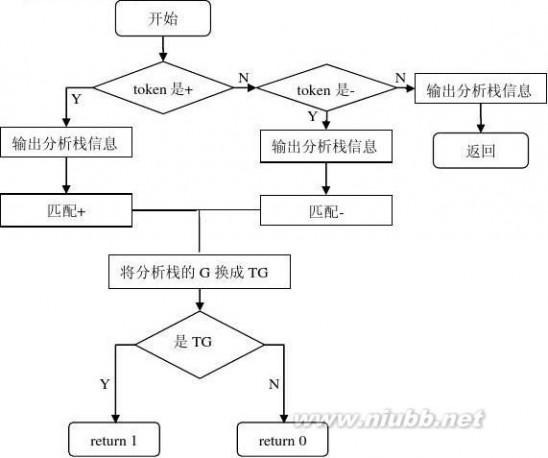
(2)G->+TG|—TG
(3)G->ε
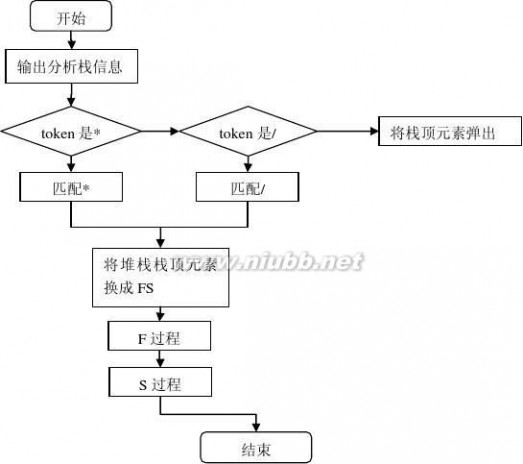
(4)T->FS
(5)S->*FS|/FS
(6)S->ε
(7)F->(E)
(8)F->i
输出的格式如下:
(1)递归下降分析程序,编制人:姓名,学号,班级
(2)输入一以#结束的符号串(包括+—*/()i#):在此位置输入符号串例如:i+i*i#
(3)输出结果:i+i*i#为合法符号串
备注:输入一符号串如i+i*#,要求输出为“非法的符号串”。
注意:
1.表达式中允许使用运算符(+-*/)、分割符(括号)、字符i,结束符#;
2.如果遇到错误的表达式,应输出错误提示信息(该信息越详细越好);
三、实验过程:
程序设计:
1.模块设计:将程序分成合理的多个模块(函数),每个模块做具体的同一事情。
2.写出(画出)设计方案:模块关系简图、流程图、全局变量、函数接口等。
程序编写:
1.定义部分:定义常量、变量、数据结构。
2.初始化:从文件将输入符号串输入到字符缓冲区中。
3.利用递归下降分析法,对每个非终结符编写函数,在主函数中调用文法开始符号的函数。
四、实验结果
递归下降 递归下降分析法
(1)程序流程图

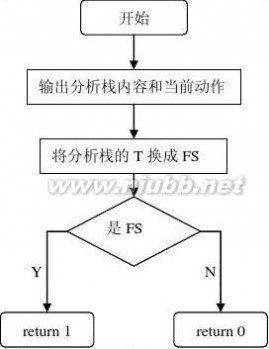
主函数main( )流程图 E( )过程流程图
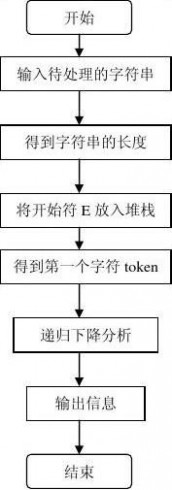
T( )过程流程图
递归下降 递归下降分析法
G( )过程流程图
F( )过程流程图
递归下降 递归下降分析法
S( )过程流程图
(2)运行结果
示例程序:
#include <stdio.h>
#include<dos.h>
#include<stdlib.h>
#include<string.h>
char a[50] ,b[50],d[500],e[10]; char ch;
int n1,i1=0,flag=1,n=5;
int E();
int E1();
int T();
int G();
int S();
int F();
void input();
void input1();
void output();
void main() /*递归分析*/
递归下降 递归下降分析法
{
int f,p,j=0;
char x;
d[0]='E';
d[1]='=';
d[2]='>';
d[3]='T';
d[4]='G';
d[5]='#';
printf("递归下降分析程序,编制人:___,____,_________\n"); printf("输入一以#结束的符号串(包括+ - * / ( ) i #,且长度小于50):"); do{
scanf("%c",&ch);
a[j]=ch;
j++;
}while(ch!='#');
n1=j;
ch=b[0]=a[0];
printf("文法\t分析串\t\t\t分析字符\t\t剩余串\n");
f=E1();
if(f==0) return ;
if (ch=='#')
{ printf("accept\n");
p=0;
x=d[p];
while(a[p]!='#')
printf("%c",a[p++]);
printf("为合法字符!\n");
}
else {
// printf("error\n");
j=0;
while(a[j]!='#')
printf("%c",a[j++]);
printf("非法字符!\n");
printf("回车返回\n");
getchar();getchar();
return;
}
printf("\n");
printf("回车返回\n");
getchar();
getchar();
}
递归下降 递归下降分析法
int E1()
{ int f,t;
printf("E-->TG\t");
flag=1;
input();
input1();
f=T();
if (f==0) return(0);
t=G();
if (t==0) return(0);
else return(1);
}
int E()
{ int f,t;
printf("E-->TG\t");
e[0]='E';e[1]='=';e[2]='>';e[3]='T';e[4]='G';e[5]='#'; output();
flag=1;
input();
input1();
f=T();
if (f==0)
return(0);
t=G();
if (t==0) return(0);
else return(1);
}
int T()
{ int f,t;
printf("T-->FS\t");
e[0]='T';e[1]='=';e[2]='>';e[3]='F';e[4]='S';e[5]='#'; output();
flag=1;
input();
input1();
f=F();
if (f==0)
return(0);
t=S();
if (t==0) return(0);
else return(1);
}
int G()
递归下降 递归下降分析法
{
int f;
if(ch=='+')
{
b[i1]=ch;
printf("G-->+TG\t");
e[0]='G';e[1]='=';e[2]='>';e[3]='+';e[4]='T';e[5]='G';e[6]='#'; output();
flag=0;
input();input1();
ch=a[++i1];
f=T();
if (f==0)
return(0);
f=G();
if(f==0)
return 0;
else return 1;
}
else if(ch=='-')
{
b[i1]=ch;
printf("G-->-TG\t");
e[0]='G';e[1]='=';e[2]='>';e[3]='-';e[4]='T';e[5]='G';e[6]='#'; output();
flag=0;
input();input1();
ch=a[++i1];
f=T();
if (f==0)
{
return(0);
}
f=G();
if(f==0)
return 0;
else return 1;
}
else
{
printf("G-->^\t");
e[0]='G';e[1]='=';e[2]='>';e[3]='^';e[4]='#';
output();
flag=1;
递归下降 递归下降分析法
input();input1();
return(1);
}
}
int S()
{
int f,t;
if(ch=='*')
{
b[i1]=ch;
printf("S-->*FS\t");
e[0]='S';e[1]='=';e[2]='>';e[3]='*';e[4]='F';e[5]='S';e[6]='#'; output();
flag=0;
input();input1();
ch=a[++i1];
f=F();
if (f==0)
return(0);
t=S();
if (t==0)
return(0);
else return(1);}
else if(ch=='/')
{
b[i1]=ch;
printf("S-->/FS\t");
e[0]='S';e[1]='=';e[2]='>';e[3]='/';e[4]='F';e[5]='S';e[6]='#'; output();
flag=0;
input();input1();
ch=a[++i1];
f=F();
if (f==0)
return(0);
t=S();
if (t==0)
return(0);
else return(1);}
else
{
递归下降 递归下降分析法
printf("S-->^\t");
e[0]='S';e[1]='=';e[2]='>';e[3]='^';e[4]='#';
output();
flag=1;
a[i1]=ch;
input();input1();
return(1);
}
}
int F()
{ int f;int j;
if(ch=='(')
{
b[i1]=ch;
printf("F-->(E)\t");
e[0]='F';e[1]='=';e[2]='>';e[3]='(';e[4]='E';e[5]=')';e[6]='#'; output();
flag=0;
input();input1();
ch=a[++i1];
f=E();
if (f==0) return(0);
if(ch==')')
{
b[i1]=ch;
printf("F-->(E)\t");
flag=0;input();input1();
ch=a[++i1];
}
else
{
printf("error\n");
j=0;
while(a[j]!='#')
printf("%c",a[j++]);
printf("非法字符!\n");
return(0);
}
}
else if(ch=='i')
{
b[i1]=ch;
printf("F-->i\t");
递归下降 递归下降分析法
e[0]='F';e[1]='=';e[2]='>';e[3]='i';e[4]='#';
output();
flag=0;input();input1();
ch=a[++i1];
}
else {
printf("error\n");
j=0;
while(a[j]!='#')
printf("%c",a[j++]);
printf("非法字符!\n");
return(0);
}
return(1);
}
void input()
{
int j=0;
for (;j<=i1-flag;j++)
printf("%c",b[j]); /*输出分析串*/ printf("\t\t\t");
printf("%c\t\t\t",ch); /*输出分析字符*/ }
void input1()
{
int j;
for (j=i1+1-flag;j<n1;j++)
printf("%c",a[j]); /*输出剩余字符*/ printf("\n");
}
void output(){ /*推导式计算*/ int m,k,j,q;
int i=0;
m=0;k=0;q=0;
i=n;
d[n]='=';d[n+1]='>';d[n+2]='#';n=n+2;i=n;
i=i-2;
while(d[i]!='>'&&i!=0) i=i-1;
i=i+1;
while(d[i]!=e[0]) i=i+1;
q=i;
m=q;k=q;
while(d[m]!='>') m=m-1;
递归下降 递归下降分析法
m=m+1;
while(m!=q) {
d[n]=d[m];m=m+1;n=n+1; }
d[n]='#';
for(j=3;e[j]!='#';j++){ d[n]=e[j];
n=n+1;
}
k=k+1;
while(d[k]!='=') {
d[n]=d[k];n=n+1;k=k+1; }
d[n]='#';
}
本文标题:递归下降-试为下面的文法构造一个递归下降的分析程序.产生式为:61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1