一 : 指数积分：指数积分-定义，指数积分-性质

在数学中，指数积分是函数的一种，它不能表示为初等函数。

指数函数积分_指数积分 -定义

[www.61k.com]对任意实数，指数积分有下定义：

E1函数（顶）和Ei函数（底）。Ei(x)=∫e^t/t dt (-∞~x)，这个积分必须用柯西主值来解释。

如果自变量是复数的情形，这个定义就变得模棱两可了 。为了避免歧义，我们使用以下的记法：

E1(x)=∫e^(-t)/t dt (z~+∞) (|ARG(z)|<π)

如果Re(z)>0，则

E1(z)=∫e^(-tz)/t dt (1~+∞) (Re(z)>0)

其中，

Ei(-x±i0)=-E1(x)减加iπ

-Ei(x)=(Ei(-x+i0)+E1(-x-i0))/2

指数函数积分_指数积分 -性质

收敛级数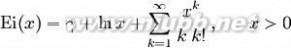
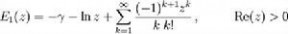
Ei(x)幂级数展开-

-
E1(x)幂级数展开-

-

其中γ是欧拉常数。渐进（发散）级数

自变量的值较大时，用以上的收敛级数来计算指数积分是困难的。在这种情况下，我们可以使用发散（或渐近）级数：

渐进级数-

-

-指数和对数的表现

E1在自变量较大时的表现类似指数函数，自变量较小时类似对数函

数。


大小关系-

-

-

这个不等式的左端在图中用红色曲线来表示，中间的黑色曲线是E1(x)，不等式的右端用蓝色曲线来表示。与其它函数的关系

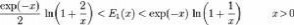
指数积分与对数积分li(x)的关系：

li(x) = Ei (ln (x))x≠ 1

另外1个有密切关系的函数，具有不同的积分限：

E1(x)=∫e^(-tx)/t dt (1~+∞) =∫e^(-t)/t dt (x~+∞)

可以延伸到负数：

Ei(-x)=-E1(x)

我们可以把2个函数都用整函数来表示：

Ein(x)=∫(1-e^(-t))/t dt (0~x)=∑(-1)^(k-1)x^k/(k*k!) (1~∞)

此函数的性质：

E1(z)=-γ-ln(z)+Ein(z) (|Arg(z)|<π)

Ei(x)=γ+ln(x)-Ein(-x) (x>0)

指数积分还可以推广为：

En(x)=∫e^(-tx)/t^n dt (1~+∞)

导数

函数En与E1的导数有以下简单的关系：

En&#39;(z)=-E(n-1)(z) (|Arg(z)|<π ,n>0)

然而，这里假设了n是整数；复数n的推广还没有在文献中报导，虽然这种推广是有可能的。

复变量的指数积分

从定义中可以看出，指数积分与三角积分之间的关系：

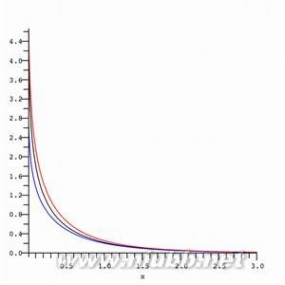
E1(ix)=-π/2+S1(x)-i*Ci(x)(x>0)

图中的黑色和红色曲线分别描述了E1(x)的实数和虚数部分。

二 : 小数：小数-定义，小数-性质

小数由整数部分、小数部分和小数点组成。当测量物体时往往会得到的不是整数的数,古人就发明了小数来补充整数小数是十进分数的一种特殊表现形式。分母是10、100、1000……的分数可以用小数表示。所有分数都可以表示成小数，小数中除无限不循环小数外都可以表示成分数。无理数为无限不循环小数。

小数_小数 -定义

把分母是10、100、1000......的分数改写成不带分母形式的数,叫做小数.
根据十进制的位值原则，把十进分数仿照整数的写法写成不带分母的形式，这样的数叫做小数．小数中的圆点叫做小数点，它是1个小数的整数部分和小数部分的分界号，小数点左边的部分是整数部分，小数点右边的部分是小数部分．整数部分是零的小数叫做纯小数，整数部分不是零的小数叫做带小数．例如0.3是纯小数，3.1是带小数．
要了解小数的意义，可从分数的意义着手，分数的意义可从子分割及合成活动来解释，当1个整体（指基准量）被等分后，在集聚其中一部份的量称为「分量」，而「分数」就是用来表示或纪录这个「分量」。例如：2/5是指1个整数被分成五等分后，集聚其中二分的「分量」。当整体被分成十等分、百等分、千等分……等时，此时的分量，就使用另外1种纪录的方法－小数。例如1/10记成0.1、2/100记成0.02、5/1000记成0.005……等。其中的「.」称之为小数点，用以分隔整数部分与无法构成整数的小数部分。整数非0者称为带小数，若为0则称纯小数。由此可知，小数的意义是分数意义的一环。
小数的读法有2种：1种是按照分数的读法来读．带小数的整数部分按整数读法读；小数部分按分数读法读．例如：0.38读作百分之三十八，14.56读作十四又百分之五十六．另1种读法，整数部分仍按整数的读法来读，小数点读作“点”，小数部分顺次读出每个数位上的数字．例如：0.45读作零点四五；56.032读作五十六点零三二．
小数大小的比较方法与整数基本相同，即从高位起，依次把相同数位上的数加以比较．
因此，比较2个小数的大小，先看它们的整数部分，整数部分大的那个数大；如果整数部分相同，十分位上的数大的那个数大；如果十分位上的数也相同，百分位上的数大的那个数大；
因为小数是十进分数，所以有下列性质：①在小数的末尾添上零或去掉零，小数的大小
不变．例如；2.4＝2.400，0.060＝0.06．②小数点移动会引起小数大小发生变化．把小数点分别向右移动一位、二位、三位…位，则小数的值分别扩大10倍、100倍、1000倍……例如：把7.4扩大10倍是74，扩大100倍是740……
如果把小数点分别向左移动一位、二位、三位…则小数的值分别缩小到原来的十分之一、百分之一、千分之一…．例如：把7.4缩小到原来的十分之一是0.74，缩小到原来的百分之一是0.074……
保留小数：按要求在舍去部分最高位进行四舍五入运算。
无限不循环小数只能用小数表示不能用分数表示，而所有的有限小数和无限循环小数均能用分数表示，小数分为有限小数和无限小数，有限小数如1/5，无限小数包括无限不循环小数（如0.010010001……）和无限循环小数（如1/3）
有理数（rationalnumber)：能精确地表示为2个整数之比的数．
如3，-98.11，5.72727272……，7/22都是有理数．
整数和通常所说的分数都是有理数．有理数还可以划分为正有理数，0和负有理数．
在数的十进制小数表示系统中，有理数就是可表示为有限小数或无限循环小数的数．这一定义在其他进位制下（如二进制）也适用．《中国大百科全书》（数学））
因此，不矛盾。
小数乘以整数：
把小数乘法转化成整数乘法计算。
先把小数扩大成整数，按照整数乘法去计算，因数扩大了多少倍，积就要缩小多少倍。
积的小数位数与被乘数的小数位数有关，被乘数有几位小数，积就有几位小数。因为要把小数乘法转化成整数乘法，被乘数扩大了多少倍，乘数不变，积也随着扩大了多少倍。因此必须再把积缩小多少倍。
计算小数乘以整数，先按照整数乘法的计算方法算出积，再看被乘数中有几位小数，就从积的右边起数出几位，点上小数点。
部分小数类型定义
纯小数：整数部分是零的小数如0.1，绝对值一定小于1。
带小数：整数部分是1或1以上的小数如1.1，绝对值一定大于等于1。
1个小数，从小数部分的某一位起，1个数字或几个数字，依次不断地重复出现，这个小数叫做循环小数。
循环节：1个循环小数的小数部分，依次不断重复出现的数字
叫做这个循环小数的循环节。例如：0.33……循环节是“3”
2.14242……循环节是“42”
纯循环小数：循环节从小数部分第一位开始的。（例如：0.666……）
混循环小数：循环节不是从小数部分第一位开始的。（例如：0.5666……）
简便记法：写循环小数时，为了简便，小数的循环部分只写出
第1个循环节。如果循环节只有1个数字，就在这个数字上加1个圆点，如果循环节有1个以上的数字，就在这个循环节的首位和末位的数字上各加1个圆点。

小数_小数 -性质

小数点的末尾添上0或者去掉0，小数的大小不变。

小数_小数 -分类

纯小数

整数部分是零的小数如0.1，绝对值一定小于1。　　如：0.12；0.945；0.403等

带小数

整数部分是1或1以上的小数如1.1，绝对值一定大于等于1。　　如：1.2345；9.45；1.43等　　1个小数，从小数部分的某一位起，1个数字或几个数字，依次不断地重复出现，这个小数叫做循环小数。

循环节

1个循环小数的小数部分，依次不断重复出现的数字　　叫做这个循环小数的循环节。例如：0.33……循环节是“3”　　2.14242……循环节是“42”　　纯循环小数：循环节从小数部分第一位开始的。（例如：0.666……）　　混循环小数：循环节不是从小数部分第一位开始的。（例如：0.5666……）

简便记法

写循环小数时，为了简便，小数的循环部分只写出　　第1个循环节。如果循环节只有1个数字，就在这个数字上加1个圆点，如果循环节有1个以上的数字，就在这个循环节的首位和末位的数字上各加1个圆点。

小数_小数 -规则

根据十进制的位值原则，把十进分数仿照整数的写法写成不带分母的形式，这样的数叫做小数．小数中的圆点叫做小数点，它是1个小数的整数部分和小数部分的分界号，小数点左边的部分是整数部分，小数点右边的部分是小数部分．整数部分是零的小数叫做纯小数，整数部分不是零的小数叫做带小数．例如0.3是纯小数，3.1是带小数.

小数_小数 -分类

小数分为纯小数,带小数,有限小数,无限小数
无限小数包括无限循环小数和无限不循环小数

小数_小数 -读法

有2种：1种是按照分数的读法来读．带小数的整数部分按整数读法读；小数部分按分数读法读．例如：0.38读作百分之三十八，14.56读作十四又百分之五十六．另1种读法，整数部分仍按整数的读法来读，小数点读作“点”，小数部分顺次读出每个数位上的数字，若几个零重复，不可只读1个0．例如：0.45读作零点四五；56.032读作五十六点零三二；1.0005读作一点零零零五．

小数_小数 -比较

小数大小的比较方法与整数基本相同，即从高位起，依次把相同数位上的数加以比较．　　因此，比较2个小数的大小，先看它们的整数部分，整数部分大的那个数大；如果整数部分相同，十分位上的数大的那个数大；如果十分位上的数也相同，百分位上的数大的那个数大；　　因为小数是十进分数，所以有下列性质：①在小数的末尾添上零或去掉零，小数的大小　　不变．例如；2.4＝2.400，0.060＝0.06．②小数点移动会引起小数大小发生变化．把小数点分别向右移动一位、二位、三位…位，则小数的值分别扩大10倍、100倍、1000倍……例如：把7.4扩大10倍是74，扩大100倍是740……　　如果把小数点分别向左移动一位、二位、三位…则小数的值分别缩小到原来的十分之一、百分之一、千分之一…...．例如：把7.4缩小到原来的十分之1是0.74，缩小到原来的百分之一是0.074……

小数_小数 -保留

小数保留小数：按要求在舍去部分最高位进行四舍五入运算。　　无限不循环小数只能用小数表示不能用分数表示，而所有的有限小数和无限循环小数均能用分数表示，小数分为有限小数和无限小数，有限小数如1/5，无限小数包括无限不循环小数（如0.010010001……）和无限循环小数（如1/3）　　（有理数（rationalnumber)：能精确地表示为2个整数之比的数．　　如3，-98.11，5.72727272……，7/22都是有理数．　　整数和通常所说的分数都是有理数．有理数还可以划分为正有理数，0和负有理数．　　在数的十进制小数表示系统中，有理数就是可表示为有限小数或无限循环小数的数．这一定义在其他进位制下（如二进制）也适用．《中国大百科全书》（数学））　　因此，不矛盾。　　小数乘以整数：　　把小数乘法转化成整数乘法计算。　　先把小数扩大成整数，按照整数乘法去计算，因数扩大了多少倍，积就要缩小多少倍。　　积的小数位数与被乘数的小数位数有关，被乘数有几位小数，积就有几位小数。因为要把小数乘法转化成整数乘法，被乘数扩大了多少倍，乘数不变，积也随着扩大了多少倍。因此必须再把积缩小多少倍。　　计算小数乘以整数，先按照整数乘法的计算方法算出积，再看被乘数中有几位小数，就从积的右边起数出几位，点上小数点。

三 : 推重比：推重比-定义，推重比-性质

推重比是发动机推力与发动机重量（力）或飞机重量（力）之比，它表示发动机或飞机单位重量（力）所产生的推力。发动机在海平面静止条件下于最大状态（加力发动机为全加力状态）所产生的推力与发动机结构重量（力）之比称为发动机推重比，是发动机的重要性能指标之一。

推重比_推重比 -定义

发动机在水平面上的最大推力和发动机的净重之比，称为发动机的推重比。飞机在海平面最大静推力与飞机起飞重量之比，称为飞行器的推重比。

推重比_推重比 -性质

喷气发动机产生的推力和所在海拔高度相关，同时飞行器自重的计算也没有统一标准，因此推重比在不同情况下的计算会产生不小差异。增大推重比有2个途径，减小飞行器自重，采用更轻的材料制造，或者是增大发动机的推力。

推重比_推重比 -应用

推重比推重比是1个综合性的性能指标，它不仅体现喷气发动机在气动热力循环方面的水平，也体现了结构方面的设计水平。它对于飞机的飞行性能和有效载荷等都有直接影响。飞机的最大平飞速度、爬升率、升限、机动性等都与飞机推重比有关。发动机推重比的跨越往往会带来新一代战斗机的出现。现代涡轮喷气发动机的推重比约为3.5～4.5；加力涡轮喷气发动机约为5～7；加力涡轮风扇发动机可达8以上；高性能的加力式涡轮风扇发动机的推重比可达12～15；用於垂直起落的升力发动机则高达16以上。进1步提高推重比是发动机发展的1个重要趋势，例如升力发动机正向20～24发展，冲压发动机在2～3倍音速时，推重比在20左右。液体火箭发动机的推重比随发动机特点和推力等级不同相差很大。对中等或大推力发动机来说，以不包括推进剂的结构重量(力)计，推重比可达70～100。固体火箭发动机除用推重比外，还用冲量比，即总冲量与装有药柱的固体火箭发动机重量(力)之比。中国的WS10推重比大概是8左右，WS15推重比可以达到10；美国的F110推重比大约是7-8，F119可以达到10，而F13五大概是10-12；通用的VAATE项目推重比可达12-15，而GEVAATE项目据说可达20。现代歼击机的飞机推重比可达1～1.25；轰炸机则为0.25～0.50。

四 : 在质疑声中小米5重新定义了“黑科技” 性价比优势也不会太长

　　摘要： 现如今小米5的参数和性价比是还不错，但一旦竞争对手照葫芦画瓢来上个差不多的菜，小米的优势就已经没有了

　　

 

　　今天(2月24日)下午，可能是最受期待的国产手机小米5正式发布了，一同发布的还有其保密工作非常彻底的“僚机”小米4S，只不过在只有300块的差价面前，后者与前者的差距，的确让其少了许多吸引力。

　　还是来谈谈小米5吧，在此之前已经有无数条曝光让其几乎已经再无新料可言，但这还不是最令人失望的，最主要的是整场发布会下来，给笔者的感觉就是这是一场很普通、甚至有点缺乏科技感的发布会，小米5也算不上年度大作，反而还显得比较中庸——没错，是真的中庸。

　　这里面固然有雷军结结巴巴的现场表现和浓重的地方口音所造成的影响，不过深入的去看，小米5的确已经不能算是一款出众的手机了。

　　小米5有没有性价比?

　　答案必然是有的，只是和以前相比，却少了一些极致的部分。

　　这里有一个蛮有趣的地方是，许多人探讨小米5性价比是否还在，看的是它是否还是1999元起步，但却忽略了一些其它的东西，或者是受到以前的惯性影响，一看到顶级芯片等硬件配置+1999元起步的售价，就觉得还不错。

　　但是时代是在进步的，当下手机行业一些热点功能——曲面屏、无边框、3D Touch、无线充电、大底传感器这些，小米5上面都没有，不可否认这其中有不少当下还是非常不实用的噱头级功能，但是更不可否认的是，这些才是在对手都已经贴身于小米作战的当下，最能凸显小米性价比竞争力的选项，然而小米一个都没有选用。

　　这里面可能出于成本的考虑，也可能是小米有意为之，但无论怎么样，这都让小米5显得不那么值得入手了，特别是在旁边vivo宣传6GB运存、OPPO展示 15分钟充满一台手机的Super VOOC技术、乐视抢发骁龙820成功还顺带搭载了超声波指纹识别方案的当下，小米在产品的吸睛程度上，的确显得落后了。

　　而且值得一提的是，1999元的小米5采用的是降频版的骁龙820处理器，主频仅1.8GHz，而Adreno 530 GPU的主频也仅为510MHz;往上的高配版则是2.15GHz主频的骁龙820+主频为624MHz的Adreno 530，而且就算是高配版的主频正常了，但是用的还是3G运存，哪哪都让人觉得缺了点什么。

　　你不要说我挑三拣四，因为小米可能希望用户看到1999元这个价位别人没有的东西，比如工艺和设计，然后哗哗哗掏银子去买，但站在用户的角度上，大部分用 户却思索的是为什么1999的小米没有这没有那，就这还叫有性价比?——而从某种意义上讲，这也是小米的品牌价值被性价比概念给绑死的体现，

　　小米重新定义了“黑科技”

　　乐视之前重新定义了“无边框”概念时，引来了一面倒的嘲讽，而今天，小米5重新定义了黑科技。

　　小米5自称的黑科技有十个，包括4轴光学防抖相机、DTI画质增强、3D陶瓷机身、全网通3.0、16颗灯省电高亮屏幕、全功能NFC等在内，但是一路看 下来，你会发现这些要不然是不太容易感知得到的东西，比如16颗灯省电高亮屏幕，要么就是几乎没有追平门槛的，比如4轴光学防抖相机、DTI画质增强这些 与供应商关系密切的新功能，总的来说，是绝对配不上黑科技名号的。

　　不得不说，黑科技这个词，在小米这里的确是被玩坏了，说句不好听的，有一种没见过世面，就拿来充数的感觉——特别是在MWC 2016的映照下，就更显如此了，看看LG G5的模块化“下巴”、看看三星的裸口 MicroUSB 情况下的IP68级别的防尘防水能力和Always On功能，这些尚且未获得“黑科技”的评价，到了小米这里，就更显得滥竽充数了。

　　为超越想象而来，但并没有超越想象

　　雷军经常说同仁堂这种百年老店是小米学习的榜样，但是就目前看，小米更像是手机行业里的快时尚品牌H&M，它固然比大牌便宜，有不错设计，也能够 捕捉到当季最in的时尚感，但是却唯独少了那种能真正领先的本领，而也正是因此，所以消费者不认可小米往高处走，就好像你H&M卖到了奢侈品的价 格，可还是现在这样的东西，怎么能说服高端层级的消费者不去选购真正的奢侈品呢?

　　这其中固然有小米作为年轻企业和互联网品牌的天生遗憾，但后天上，小米却也显得有些不思进取。比如去年在MIUI升级、红米Note 2发布数月后推出红米Note 3等问题上的失策，其实就可以看得出来，小米有些麻痹，或者说是积重难返了。

　　现如今小米5的参数和性价比是还不错，但一旦竞争对手照葫芦画瓢来上个差不多的菜，小米的优势就已经没有了——不要再说MIUI是小米的护城河了，在今天这个行业里，MIUI给小米带来的胜算，已经远不如一两年前那么稳妥了。

　　吐槽了这么多，其实不是笔者做梦想用2000元买到5000元的手机，而是说站在小米的角度上，这些的确是个问题，要知道的是，5000元的高端机，其 80%的功能都可以在2000元甚至更低的机器上实现，而剩下的20%则是决定用户愿不愿意掏多余3000块钱的关键，这部分拷问的不是成本和用料，而是实实在在的需求。但很明显，小米目前还不具备一个绝对确保用户离不开的地方。

　　而悲剧的是，决定手机厂商能否存活到最后时候的关键，恰恰就是这20%的需求。

本文标题：等比数列的定义及性质-指数积分：指数积分-定义，指数积分-性质
本文地址： http://www.61k.com/1069516.html