一 : 光干涉
物理学干涉是指:满足一定条件的两列相干光波相遇叠加区域某些点的光振动始终加强某些点的光振动始终减弱即在干涉区域内振动强度有稳定的空间分布。
干涉 (物理学)
维基百科,自由的百科全书
跳转至: 导航、 搜索
 在水波槽里,两个点波源共同产生的干涉图样。
在水波槽里,两个点波源共同产生的干涉图样。物理学中,干涉是两列或两列以上的波在空间中重叠时发生叠加从而形成新波形的现象。
例如采用光学分束器将一束来自单色点光源的光分成两束后,再让它们在空间中的某个区域内重叠,将会发现在重叠区域内的光强并不是均匀分布的:其明暗程度随其在空间中位置的不同而变化,最亮的地方超过了原先两束光的光强之和,而最暗的地方光强有可能为零,这种光强的重新分布被称作“干涉条纹”。在历史上,干涉现象及其相关实验是证明光的波动性的重要依据[1],但光的这种干涉性质直到十九世纪初才逐渐被人们发现,主要原因是相干光源的不易获得。
为了获得可以观测到可见光干涉的相干光源,人们发明制造了各种产生相干光的光学器件以及干涉仪,这些干涉仪在当时都具有非常高的测量精度:阿尔伯特·迈克耳孙就借助迈克耳孙干涉仪完成了著名的迈克耳孙-莫雷实验,得到了以太风观测的零结果[2]。而在二十世纪六十年代之后,激光这一高强度相干光源的发明使光学干涉测量技术得到了前所未有的广泛应用,在各种精密测量中都能见到激光干涉仪的身影。现在人们知道,两束电磁波的干涉是彼此振动的电场强度矢量叠加的结果,而由于光的波粒二象性,光的干涉也是光子自身的几率幅叠加的结果。
目录[隐藏] |
波的叠加 | 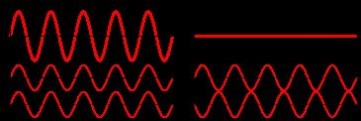 | |
| 波 1 | ||
| 波 2 | ||
两列波在同一介质中传播发生重叠时,重叠范围内介质的质点同时受到两个波的作用。若波的振幅不大,此时重叠范围内介质质点的振动位移等于各别波动所造成位移的矢量和,这称为波的叠加原理。若两波的波峰(或波谷)同时抵达同一地点,称两波在该点同相,干涉波会产生最大的振幅,称为相长干涉(建设性干涉);若两波之一的波峰与另一波的波谷同时抵达同一地点,称两波在该点反相,干涉波会产生最小的振幅,称为相消干涉(摧毁性干涉)。

 激光的产生机理是受激辐射,它决定了激光本身即具有非常优秀的相干性。
激光的产生机理是受激辐射,它决定了激光本身即具有非常优秀的相干性。理论上,两列无限长的单色波的叠加总是能产生干涉,但实际物理模型中产生的波列不可能是无限长的,并从波产生的微观机理来看,波的振幅和相位都存在有随机涨落,从而现实中不存在严格意义的单色波。例如太阳所发出的光波来源于光球层的电子与氢原子的相互作用,每一次作用的时间都在10-9秒的量级,则对于两次发生时间间隔较远所产生的波列而言,它们无法彼此发生干涉。基于这个原因,可以认为太阳是由很多互不相干的点光源组成的扩展光源。从而,太阳光具有非常宽的频域,其振幅和相位都存在着快速的随机涨落,通常的物理仪器无法跟踪探测到变化如此之快的涨落,因而我们无法通过太阳光观测到光波的干涉。类似地,对于来自不同光源的两列光波,如果这两列波的振幅和相位涨落都是彼此不相关的,我们称这两列波不具有相干性[3]。相反,如果两列光波来自同一点光源,则这两列波的涨落一般是彼此相关的,此时这两列波是完全相干的。
如要从单一的不相干波源产生相干的两列波,可以采用两种不同的方法:一种称为波前分割法,即对于几何尺寸足够小的波源,让它产生的波列通过并排放置的狭缝,根据惠更斯-菲涅耳原理,这些在波前上产生的子波是彼此相干的;另一种成为波幅分割法,用半透射、半反射的半镀银镜,可以将光波一分为二,制造出透射波与反射波。如此产生的反射波和透射波来自于同一波源,并具有很高的相干性,这种方法对于扩展波源同样适用[3]。
两束光发生干涉后,干涉条纹的光强分布与两束光的光程差/相位差有关:当相位差时光强最大;当相位差
时光强最小。从光强最大值和最小值的和差值可以定义干涉可见度作为干涉条纹清晰度的量度。
光作为电磁波,它的强度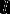 定义为在单位时间内,垂直于传播方向上的单位面积内能量对时间的平均值,即玻印亭矢量对时间的平均值[4]:
定义为在单位时间内,垂直于传播方向上的单位面积内能量对时间的平均值,即玻印亭矢量对时间的平均值[4]:
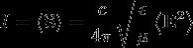
从而光强可以用 这个量来表征。对于单色光波场,电矢量
这个量来表征。对于单色光波场,电矢量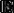 可以写为
可以写为

这里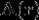 是复振幅矢量,在笛卡尔直角坐标系下可以写成分量的形式
是复振幅矢量,在笛卡尔直角坐标系下可以写成分量的形式 。
。
这里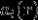 是在三个分量上的(实)振幅,对于平面波
是在三个分量上的(实)振幅,对于平面波 ,即振幅在各个方向上是常数。
,即振幅在各个方向上是常数。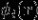 是在三个分量上的相位,
是在三个分量上的相位,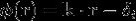 ,
,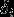 是表征偏振的常数。
是表征偏振的常数。
要计算这个平面波的光强,则先计算电场强度的平方:

对于远大于一个周期的时间间隔内,上式中前两项的平均值都是零,因此光强为

对于两列频率相同的单色平面波 、
、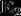 ,如果它们在空间中某点发生重叠,则根据叠加原理,该点的电场强度是两者的矢量和:
,如果它们在空间中某点发生重叠,则根据叠加原理,该点的电场强度是两者的矢量和:
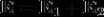
则在该点的光强为
 。
。其中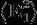 、
、 是两列波各自独立的光强,而
是两列波各自独立的光强,而 是干涉项。我们用、表示两列波的复振幅,则干涉项中可以写为
是干涉项。我们用、表示两列波的复振幅,则干涉项中可以写为
前两项对时间取平均值仍然为零,从而干涉项对光强的贡献为
根据前面复振幅的定义,、可以在笛卡尔坐标系下分解为
和
将分量形式代入上面干涉项的光强,可得
倘若在各个方向上,两者的相位差都相同并且是定值,即
其中是单色光的波长,是两列波到达空间中同一点的光程差。
此时干涉项对光强的贡献为
光波是电矢量垂直于传播方向的横波,这里考虑一种简单又不失一般性的情形:线偏振光,电矢量位于x轴上,传播方向为z轴方向,则两列波在其他方向上的振幅都为零:
代入总光强公式:
因此干涉后的光强是相位差的函数,当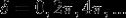 时有极大值;当
时有极大值;当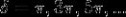 时有极小值。
时有极小值。
特别地,当两列波光强相同即时,上面公式可化简为
显然,对于不同的干涉情形,产生的极大值和极小值差异是不同的。由此可以定义条纹的可见度作为条纹清晰度的量度:
虽然以上的讨论是基于两列波都是线偏振光的假设,但对于非偏振光也成立,这是由于自然光可以看作是两个互相垂直的线偏振光的叠加。
 杨氏双缝实验的几何示意图
杨氏双缝实验的几何示意图杨氏双缝实验是最早被提出的光的干涉演示实验(托马斯·杨,1801年),这一实验的重要意义在于它是对光的波动说的有力支持,由于实验观测到的干涉条纹是61阅读[79]。这些干涉阵列平时都进行着独立的观测,但在一些特殊项目中可以实现同时性的观测,从而形成全球性的超长基线干涉。
|access date=(帮助)|access date=(帮助)二 : 白光干涉
白光干涉
迈克尔逊干涉仪中的两束相干光各有一段光路在空气是分开的,在其中的一支光路中放进被研究对象而不会影响另一支光路,据此,本实验将用它测量透明薄片的厚度或折射率。(www.61k.com]
[实验目的]
1、学习一种测量透明薄片厚度或折合率的方法;
2、进一步了解光的干涉现象及其形成条件;
3、学习调节光路的方法。
[实验原理]
首先了解迈克尔逊干涉仪产生等倾干涉和等后干涉的原理(见迈克尔逊干涉其他实验内容)。
迈克尔逊干涉仪作为测量波长的最常见实验仪器,使用氦氖激光器观察非定域干涉条纹或使用钠光源观察定域干涉条纹。通常情况下,我们看到的都是等倾干涉,由于光程差与波长的关系,此时,用白光作光源时,由于各种波长的光所产生的干涉条纹明暗交错重叠,无法观察到可见的条纹。结合迈克尔逊干涉仪产生干涉的原理,可以发现,移动M1与M2’大至重合时,视场中会出现直线干涉条纹,我们称之为等厚干涉条纹,此时换上白光光源,即可见到彩色直条纹,其中中央为一黑(暗)条纹,两旁对称分布的彩色条纹,稍远处即看不到任何条纹。所以找到等光程位置,是观察到白光干涉条纹的必要条件。
由式:
Δ=2dcosδ=2d(1?2sin2
≈2d(1?δ2) (1) δ2
2)=2d?dδ2
白光干涉 白光干涉
可知,在中央条纹位置,dδ可忽略,则Δ=2d,所以中央为直线条纹。[www.61k.com)
白光干涉的主要应用内容有对一透明薄片的测量,当正常调出彩色条纹时,我们在光路中放置一折射率为n,厚度为ι的均匀透明薄片,由于光程发生的改变:Δ′=l(n-1),原所见的条纹移出视场,将M1向G1方向前移Δd=Δ′/2,使彩色条纹重现,由式:
Δ'
Δd==l(n?1) (2) 2
给定n,读出Δd,可计算出透明薄片的厚度ι,反之给定透明薄片厚度ι,可计算出n。
[实验步骤]
1、 按干涉仪说明书,以氦氖激光器作光源为例,用投影屏观察,先调出等倾圆条纹,并使条纹基本居中。
2、 转动粗动手轮,使条纹逐渐变粗,当圆条纹变成直条纹时(从一个弯曲方向向另一个弯曲方向改变时),调节固定镜的两个微调螺钉,使直条纹变成铅垂方向。
3、 移去激光,换用白光光源;移去投影屏,略微转动微动手轮(不能超过一圈,否则说明第2步未调好),转动方向为向观察者方向转(即逆时针方向),直接用眼观察,在视场中可见彩色直条纹。
4、
亮度。 调节白光光源的调光钮,使看到的彩色条纹具有较好的对比度和适当的
5、 仍调节固定镜的两个微调螺钉,使直条纹成铅垂方向(便于确定位置),读出此时位置值d1。
6、 在移动镜前放置薄片,注意使之尽量与光路垂直,即与移动镜平行,此时彩色条纹消失。
白光干涉 白光干涉
7、 继续逆时针转动微动手轮,直至彩色条纹复又出现,仍以中央黑色纹为准,读出此时的位置值d2。[www.61k.com)
8、 Δd=d2-d1,由式(2)计算出薄片厚度l。
[实验注意事项]
1、于薄片材料为石英,即薄又脆,实验过程中务必轻拿轻放。
2、薄片的两面平行度不是很高,所以加入薄片后观察的彩色条纹会有弯曲现象。 3、个测量过程中,微动手轮必须是同一方向转动,否则由于空程的影响,精度将很差。
4、 动手轮每转动一圈为0.01mm,当薄片厚度为0.3mm时,也即微动手轮须转过30圈,而彩色条纹的位置点很精确,所以在将近的位置时,手轮要缓慢转动,否则彩色条纹一晃而过不易找到。
[思考题]
1、测量薄片厚度为什么必须用白光而不用单色光?
三 : 白光干涉
白光干涉
迈克尔逊干涉仪中的两束相干光各有一段光路在空气是分开的,在其中的一支光路中放进被研究对象而不会影响另一支光路,据此,本实验将用它测量透明薄片的厚度或折射率。
[实验目的]
1、学习一种测量透明薄片厚度或折合率的方法;
2、进一步了解光的干涉现象及其形成条件;
3、学习调节光路的方法。
[实验原理]
首先了解迈克尔逊干涉仪产生等倾干涉和等后干涉的原理(见迈克尔逊干涉其他实验内容)。
迈克尔逊干涉仪作为测量波长的最常见实验仪器,使用氦氖激光器观察非定域干涉条纹或使用钠光源观察定域干涉条纹。通常情况下,我们看到的都是等倾干涉,由于光程差与波长的关系,此时,用白光作光源时,由于各种波长的光所产生的干涉条纹明暗交错重叠,无法观察到可见的条纹。结合迈克尔逊干涉仪产生干涉的原理,可以发现,移动M1与M2’大至重合时,视场中会出现直线干涉条纹,我们称之为等厚干涉条纹,此时换上白光光源,即可见到彩色直条纹,其中中央为一黑(暗)条纹,两旁对称分布的彩色条纹,稍远处即看不到任何条纹。所以找到等光程位置,是观察到白光干涉条纹的必要条件。
由式:
Δ=2dcosδ=2d(1?2sin2
≈2d(1?δ2) (1) δ2
2)=2d?dδ2
可知,在中央条纹位置,dδ可忽略,则Δ=2d,所以中央为直线条纹。
白光干涉的主要应用内容有对一透明薄片的测量,当正常调出彩色条纹时,我们在光路中放置一折射率为n,厚度为ι的均匀透明薄片,由于光程发生的改变:Δ′=l(n-1),原所见的条纹移出视场,将M1向G1方向前移Δd=Δ′/2,使彩色条纹重现,由式:
Δ'
Δd==l(n?1) (2) 2
给定n,读出Δd,可计算出透明薄片的厚度ι,反之给定透明薄片厚度ι,可计算出n。
[实验步骤]
1、 按干涉仪说明书,以氦氖激光器作光源为例,用投影屏观察,先调出等倾圆条纹,并使条纹基本居中。
2、 转动粗动手轮,使条纹逐渐变粗,当圆条纹变成直条纹时(从一个弯曲方向向另一个弯曲方向改变时),调节固定镜的两个微调螺钉,使直条纹变成铅垂方向。
3、 移去激光,换用白光光源;移去投影屏,略微转动微动手轮(不能超过一圈,否则说明第2步未调好),转动方向为向观察者方向转(即逆时针方向),直接用眼观察,在视场中可见彩色直条纹。
4、
亮度。 调节白光光源的调光钮,使看到的彩色条纹具有较好的对比度和适当的
5、 仍调节固定镜的两个微调螺钉,使直条纹成铅垂方向(便于确定位置),读出此时位置值d1。
6、 在移动镜前放置薄片,注意使之尽量与光路垂直,即与移动镜平行,此时彩色条纹消失。
7、 继续逆时针转动微动手轮,直至彩色条纹复又出现,仍以中央黑色纹为准,读出此时的位置值d2。
8、 Δd=d2-d1,由式(2)计算出薄片厚度l。
[实验注意事项]
1、于薄片材料为石英,即薄又脆,实验过程中务必轻拿轻放。
2、薄片的两面平行度不是很高,所以加入薄片后观察的彩色条纹会有弯曲现象。 3、个测量过程中,微动手轮必须是同一方向转动,否则由于空程的影响,精度将很差。
4、 动手轮每转动一圈为0.01mm,当薄片厚度为0.3mm时,也即微动手轮须转过30圈,而彩色条纹的位置点很精确,所以在将近的位置时,手轮要缓慢转动,否则彩色条纹一晃而过不易找到。
[思考题]
1、测量薄片厚度为什么必须用白光而不用单色光?
四 : 白光的干涉条纹

光的干涉现象是光的波动学说的最好例证。[www.61k.com]在著名的杨氏双缝干涉实验中,成功地推导出在两缝间的距离和缝到屏的长度不变时,相邻两条亮纹(或暗纹)
间的距离与波长的正比关系。
如用白光做光源,由于其中各色光的波长不同,各色光所得到的干涉图样中,相邻两条亮纹(或暗纹)间的距离也不同,因此,在中央白色亮纹两边出现彩色
条纹。图为单色光和复色光分别产生的干涉图样。
图中可见,在可见光范围内,红光的波长最长,对应的条纹间距最大;紫光
的波长最短,对应的条纹间距最小。
本文标题:白光干涉-光干涉61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1