一 : 格兰杰因果关系检验

格兰杰因果关系检验 Granger Test of Causality

1、原理
? 自回归分布滞后模型揭示：某变量的变化受其 自回归分布滞后模型揭示： 自身及其他变量过去行为的影响。 自身及其他变量过去行为的影响。 ? 当两个变量在时间上有先导 当两个变量在时间上有先导——滞后关系时， 滞后关系时， 滞后关系时 可以从统计上考察这种关系是单向的还是双向。 可以从统计上考察这种关系是单向的还是双向。
–如果主要是一个变量过去的行为在影响另一个变量 如果主要是一个变量过去的行为在影响另一个变量 的当前行为，存在单向关系； 的当前行为，存在单向关系； –如果双方的过去行为在相互影响着对方的当前行为， 如果双方的过去行为在相互影响着对方的当前行为， 如果双方的过去行为在相互影响着对方的当前行为 存在双向关系。 存在双向关系。

? 向量自回归分布滞后模型可以用于变量间关系 的检验。 的检验。

2、格兰杰因果关系检验
Yt = Xt =

∑α
i =1 m i =1

m

i

X t ?i + +

∑βY
i =1 i

m

t?i

+ μ 1t

∑λY
i

t ?i

∑δ
i =1

m

i

X t ?i + μ 2t

X对Y有单向影响：α整体不为零，而λ整体为零； 对 有单向影响 有单向影响： 整体不为零， 整体为零； Y对X有单向影响：λ整体不为零，而α 整体为零； 对 有单向影响 有单向影响： 整体不为零， 整体为零； Y与X间存在双向影响：α和λ整体不为零； 与 间存在双向影响 间存在双向影响： 整体不为零； Y与X间不存在影响：α和λ整体为零。 与 间不存在影响： 整体为零。 间不存在影响

? 格兰杰检验是通过受约束的F检验完成的。如: 格兰杰检验是通过受约束的 检验完成的。 检验完成的
Yt =

∑α
i =1

m

i

X t ?i +

∑βY
i =1 i

m

t ?i

+ μ 1t

H 0 : α1 = α 2 = ? = α m = 0

( RSS R ? RSS U ) / m F = RSS U /( n ? k )
如果F>Fα(m,n-k) ，则拒绝原假设。 则拒绝原假设。 如果 如果F<Fα(m,n-k) ，则不拒绝原假设。 α 则不拒绝原假设。 如果

Xt =

∑λY
i =1 i

m

t ?i

+

∑δ
i =1

m

i

X t ?i + μ 2t

H 0 : λ1 = λ 2 = ? = λ m = 0

( RSS R ? RSS U ) / m F = RSS U /( n ? k )
如果F>Fα(m,n-k) ，则拒绝原假设。 则拒绝原假设。 如果 如果F<Fα(m,n-k) ，则不拒绝原假设。 则不拒绝原假设。 如果

? 格兰杰因果关系检验对于滞后期长度的选择有 时很敏感。 时很敏感。不同的滞后期可能会得到完全不同 的检验结果。 的检验结果。 ? 一般首先以模型随机误差项不存在序列相关为 标准选取滞后期，然后进行因果关系检验。 标准选取滞后期，然后进行因果关系检验。

3、例 例
检验1978~2006年间实际可支配收入（X）与居 民实际消费总支出(Y)之间的因

果关系。

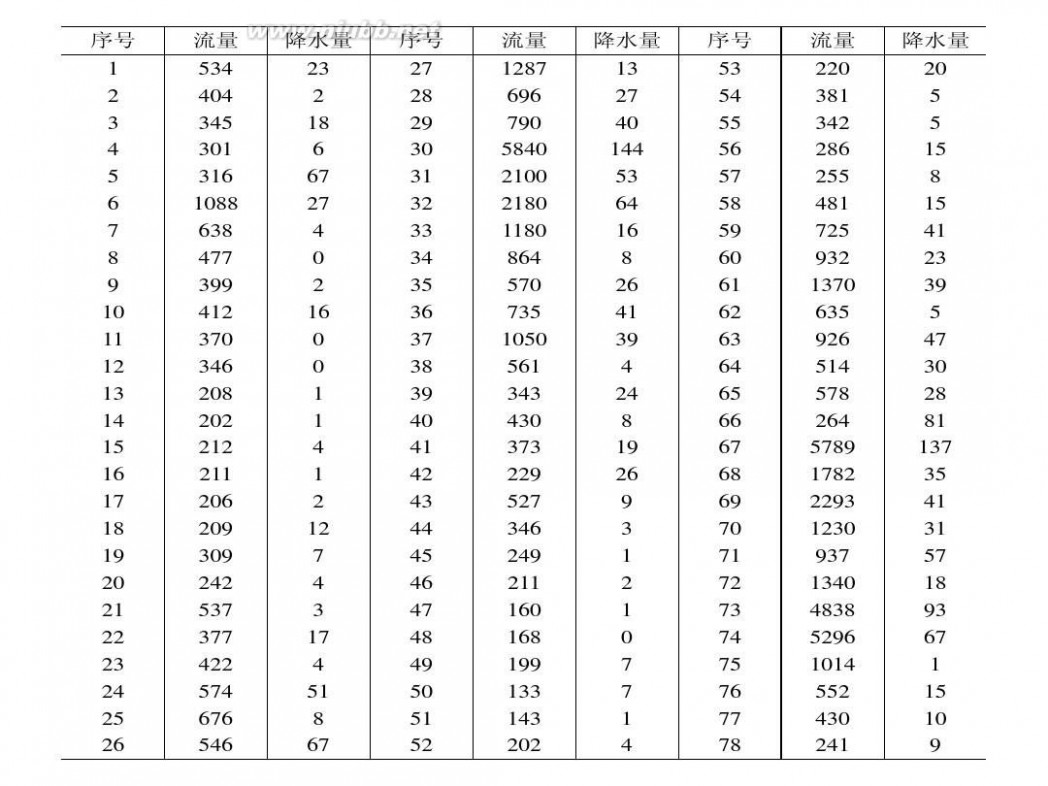
数据

选择Granger检验 检验 选择

选择检验的序列

确定滞后阶数（ 阶 确定滞后阶数（1阶）

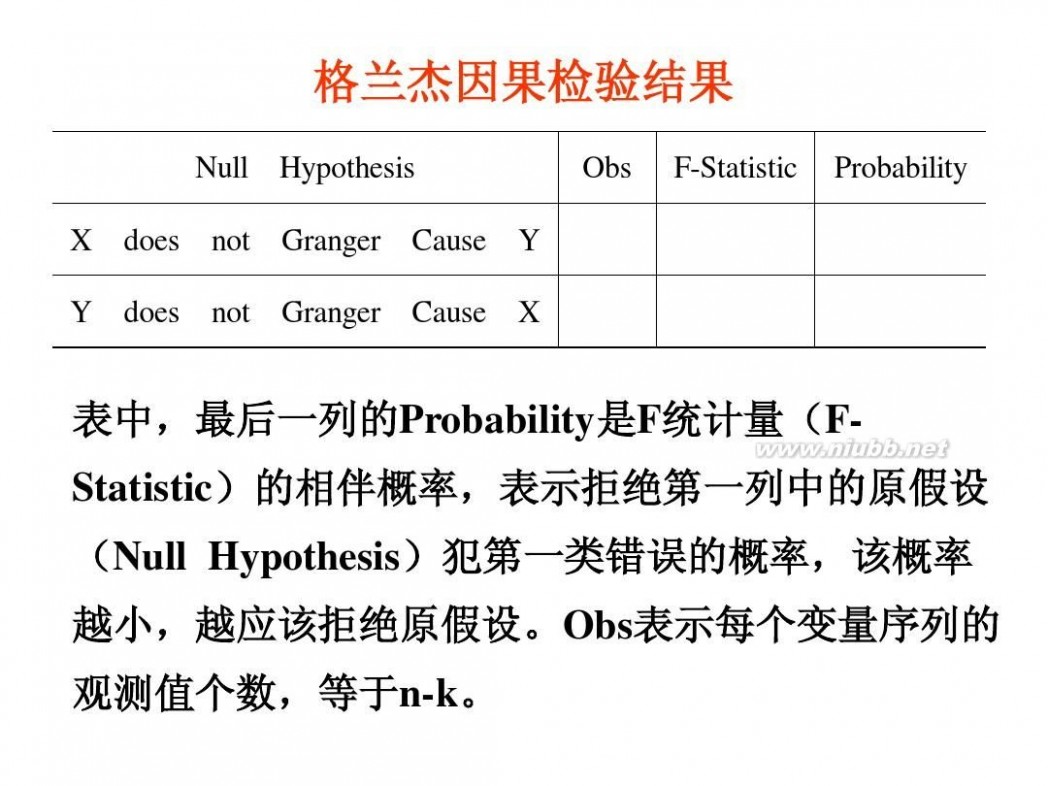
检验结果

由相伴概率知，在5%的显著性水平下，既拒绝“X不是Y的格兰杰原 因”的假设,也拒绝“Y不是X的格兰杰原因”的假设。因此，从1阶滞后 的情况看，可支配收入X的增长与居民消费支出Y增长互为格兰杰原因 。 从检验模型随机干扰项1阶序列相关的LM检验看，以Y为被解释变量 的模型的LM=0.897，对应的伴随概率P= 0.343，表明在5%的显著性水平 下，该检验模型不存在序列相关性；但是，以X为被解释变量的模型的 LM=11.37，对应的伴随概率P= 0.001，表明在5%的显著性水平下，该检 验模型存在严重的序列相关性。

检验结果

从2阶滞后期开始，检验模型都拒绝了“X不是Y的格兰杰原因”的假 设，而不拒绝“Y不是X的原因”的假设。 滞后阶数为2或3时，两类检验模型都不存在序列相关性。 由赤池信息准则，发现滞后2阶检验模型拥有较小的AIC值。 可判断：可支配收入 是居民消费支出 的格兰杰原因，而不是相反， 可支配收入X是居民消费支出 的格兰杰原因， 可支配收入 是居民消费支出Y的格兰杰原因 而不是相反， 即国民收入的增加更大程度地影响着消费的增加。 即国民收入的增加更大程度地影响着消费的增加。

二 : 格兰杰因果关系检验

格兰杰因果关系检验 一、经济变量之间的因果性问题

计量经济模型的建立过程，本质上是用回归分析工具处理一个经济变量对其他经济变量的依存性问题，但这并不是暗示这个经济变量与其他经济变量间必然存在着因果关系。(www.61k.com]

由于没有因果关系的变量之间常常有很好的回归拟合，把回归模型的解释变量与被解释变量倒过来也能够拟合得很好，因此回归分析本身不能检验因果关系的存在性，也无法识别因果关系的方向。

假设两个变量，比如国内生产总值GDP和广义货币供给量M，各自都有滞后的分量GDP（-1），GDP（-2）…，M（-1），M（-2），…，显然这两 个变量都存在着相互影响的关系。但现在的问题是：究竟是M引起GDP的变化，还是GDP引起M的变化，或者两者间相互影响都存在反馈，即M引起GDP的变 化，同时GDP也引起M的变化。这些问题的实质是在两个变量间存在时间上的先后关系时，是否能够从统计意义上检验出因果性的方向，即在统计上确定GDP是 M的因，还是M是GDP的因，或者M和GDP互为因果。

因果关系研究的有趣例子是回答“先有鸡还是先有蛋”的问题。1988年有两位学者Walter N. Thurman和Mark E. Fisher用美国1930——1983年鸡蛋产量（EGGS）和鸡的产量（CHICKENS）的年度数据，对此问题进行了统计研究。他们运用格兰杰的方 法检验鸡和蛋之间的因果关系，结果发现，鸡生蛋的假设被拒绝，而蛋生鸡的假设成立，因此，蛋为因，鸡为果，也就是先有蛋。他们并建议作其他诸如“谁笑在最 后谁笑得最好”、“骄傲是失败之母”之类的格兰杰因果检验。

二、格兰杰因果关系检验

经济学家开拓了一种可以用来分析变量之间的因果的办法，即格兰杰因果关系检验。该检验方法为2003年诺贝尔经济学奖得主克莱夫〃格兰杰（Clive W. J. Granger）所开创，用于分析经济变量之间的因果关系。他给因果关系的定义为“依赖于使用过去某些时点上所有信息的最佳最小二乘预测的方差。”

在时间序列情形下，两个经济变量X、Y之间的格兰杰因果关系定义为：若在包含了变量X、Y的过去信息的条件下，对变量Y的预测效果要优于只单独由Y的过去信息对Y进行的预测效果，即变量X有助于解释变量Y的将来变化，则认为变量X是引致变量Y的格兰杰原因。

格兰杰因果关系检验 格兰杰因果关系检验

[www.61k.com）

三 : 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

格兰杰因果关系检验 3.2 格兰杰因果关系检验(计量经济学-武汉大学 刘伟)

四 : 格兰杰因果关系检验：格兰杰因果关系检验-相关背景，格兰杰因果关系检验

经济学家开拓了一种试图分析变量之间的格兰杰因果关系的办法，即格兰杰因果关系检验。该检验方法为2003年诺贝尔经济学奖得主克莱夫·格兰杰（Clive W. J. Granger）所开创，用于分析经济变量之间的格兰杰因果关系。他给格兰杰因果关系的定义为“依赖于使用过去某些时点上所有信息的最佳最小二乘预测的方差。”

格兰杰检验_格兰杰因果关系检验 -相关背景

（www.61k.com］格兰杰本人在其2003年获奖演说中强调了其引用的局限性，以及“很多荒谬论文的出现”（Of course, many ridiculous papers appeared）。由于其统计学本质上是对平稳时间序列数据1种预测，仅适用于计量经济学的变量预测，不能作为检验真正因果性的判据。

在时间序列情形下，2个经济变量X、Y之间的格兰杰因果关系定义为：若在包含了变量X、Y的过去信息的条件下，对变量Y的预测效果要优于只单独由Y的过去信息对Y进行的预测效果，即变量X有助于解释变量Y的将来变化，则认为变量X是引致变量Y的格兰杰原因。

进行格兰杰因果关系检验的1个前提条件是时间序列必须具有平稳性，否则可能会出现虚假回归问题。因此在进行格兰杰因果关系检验之前首先应对各指标时间序列的平稳性进行单位根检验(unit root test)。常用增广的迪基—富勒检验(ADF检验)来分别对各指标序列的平稳性进行单位根检验。

格兰杰检验_格兰杰因果关系检验 -公式介绍

格兰杰因果关系检验假设了有关y和x每一变量的预测的信息全部包含在这些变量的时间序列之中。检验要求估计以下的回归：

格兰杰因果关系检验

（1）

格兰杰因果关系检验

（2）

其中白噪音u1t 和u2t假定为不相关的。

式（1）假定当前y与y自身以及x的过去值有关，而式（2）对x也假定了类似的行为。

对式（1）而言，其零假设H0 ：α1=α2=…=αq=0。

对式（2）而言，其零假设H0 ：δ1=δ2=…=δs=0。

分4种情形讨论：

（1）x是引起y变化的原因，即存在由x到y的单向因果关系。若式（1）中滞后的x的系数估计值在统计上整体的显着不为零，同时式（2）中滞后的y的系数估计值在统计上整体的显着为零，则称x是引起y变化的原因。

（2）y是引起x变化的原因，即存在由y到x的单向因果关系。若式（2）中滞后的y的系数估计值在统计上整体的显着不为零，同时式（1）中滞后的x的系数估计值在统计上整体的显着为零，则称y是引起x变化的原因。

（3）x和y互为因果关系，即存在由x到y的单向因果关系，同时也存在由y到x的单向因果关系。若式（1）中滞后的x的系数估计值在统计上整体的显着不为零，同时式（2）中滞后的y的系数估计值在统计上整体的显着不为零，则称x和y间存在反馈关系，或者双向因果关系。

（4）x和y是独立的，或x与y间不存在因果关系。若式（1）中滞后的x的系数估计值在统计上整体的显着为零，同时式（2）中滞后的y的系数估计值在统计上整体的显着为零，则称x和y间不存在因果关系。

三、格兰杰因果关系检验的步骤

（1）将当前的y对所有的滞后项y以及别的什么变量（如果有的话）做回归，即y对y的滞后项yt-1，yt-2，…，yt-q及其他变量的回归，但在这一回归中没有把滞后项x包括进来，这是1个受约束的回归。然后从此回归得到受约束的残差平方和RSSR。

（2）做1个含有滞后项x的回归，即在前面的回归式中加进滞后项x，这是1个无约束的回归，由此回归得到无约束的残差平方和RSSUR。

（3）零假设是H0：α1=α2=…=αq=0，即滞后项x不属于此回归。

（4）为了检验此假设，用F检验，即：

它遵循自由度为q和(n-k)的F分布。在这里，n是样本容量，q等于滞后项x的个数，即有约束回归方程中待估参数的个数，k是无约束回归中待估参数的个数。

（5）如果在选定的显着性水平α上计算的F值超过临界值Fα，则拒绝零假设，这样滞后x项就属于此回归，表明x是y的原因。

（6）同样，为了检验y是否是x的原因，可将变量y与x相互替换，重复步骤（1）～（5）。

格兰杰因果关系检验对于滞后期长度的选择有时很敏感。其原因可能是被检验变量的平稳性的影响，或是样本容量的长度的影响。不同的滞后期可能会得到完全不同 的检验结果。因此，一般而言，常进行不同滞后期长度的检验，以检验模型中随机干扰项不存在序列相关的滞后期长度来选取滞后期。

格兰杰检验的特点决定了它只能适用于时间序列数据模型的检验，无法检验只有横截面数据时变量间的关系。

可以看出，我们所使用的Granger因果检验与其最初的定义已经偏离甚远，削减了很多条件（并且由回归分析方法和F检验的使用我们可以知道还增强了若干 条件），这很可能会导致虚假的格兰杰因果关系。因此，在使用这种方法时，务必检查前提条件，使其尽量能够满足。此外，统计方法并非万能的，评判1个对象，往往需 要多种角度的观察。正所谓“兼听则明，偏听则暗”。诚然真相永远只有1个，但是也要靠科学的探索方法。

值得注意的是，格兰杰因果关系检验的结论只是1种预测，是统计意义上的“格兰杰因果性“，而不是真正意义上的因果关系，不能作为肯定或否定因果关系的根据。当然，即使格兰杰因果关系不等于实际因果关系，也并不妨碍其参考价值。因为在经济学中，统计意义上的格兰杰因果关系也是有意义的，对于经济预测等仍然能起一些作用。

由于假设检验的零假设是不存在因果关系，在该假设下F统计量服从F分布，因此严格地说，该检验应该称为格兰杰非因果关系检验。

本文标题：格兰杰因果关系检验-格兰杰因果关系检验
本文地址： http://www.61k.com/1140463.html