一 : 论文数字序号的使用
我们在写文章经常会用一些数字序号,用得好,能使我们的文章有条有理,眉目清楚;用得不好,让人看着别扭,甚至会影响文章的质量。可见序号也是文章的一个重要组成部分,它的规范与否同样很重要。在评选论文时,常常会为一些文章感到惋惜,内容、文字很精彩,可数字序号的运用不规范或者混乱,让人间空一个汉字位置即可。
六、数字序号前后一般不再用其他项目符号;
七、数字序号的级别顺序为:“一”“二”“三”——“ ㈠”“㈡”“㈢”——“1” “2”“ 3”——“⑴”“⑵”“⑶”——“①”“②”“③”等。
常见不规范之序号有:
1、 | (一)、 | ⑴、 | ①、 | 1、 | 第一: | 第一、 |
2、 | (二)、 | ⑵、 | ②、 | 2、 | 第二: | 第二、 |
3、 | (三)、 | ⑶、 | ③、 | 3、 | 第三: | 第三、 |
正确的用法如下:
1. | (一) | ⑴ | ① | 第一, |
2. | (二) | ⑵ | ② | 第二, |
3. | (三) | ⑶ | ③ | 第三, |
在论文中正确地运用序号,能使文章层次清楚,逻辑分明,便于读者阅读和引述,但目前教师撰写论文在序号的写法上存在着不少的误区,如:层次大小不分、中文数字与阿拉伯数字混用、前后序号形式不统一,等等。下面就论文中几种常见的序号写法作一说明:
一、正文层次标题序号
正文层次标题序号要注意大小分级。如一级标题序号可用汉字一、二、三……,二级标题序号可用汉字加括号(一)(二)(三)……,三级标题序号可用阿拉伯数字1、2、3……,四级标题序号可用阿拉伯数字加括号(1)(2)(3)……,五级标题序号可用阿拉伯数字加右括号1)2)3)……,若还有六、七级序码还可采用大小写英文字母。注意加了括号的序号后就不要再加点号了。
理科类论文的各层次标题还可用阿拉伯数字连续编码,不同层次的2个数字之间用下圆点(.)分隔开,末位数字后面不加点号。如“1”,“1.2”,“3.5.1”等;各层次的标题序号均左顶格排写,最后一个序号之后空一个字距接排标题。如“5.3.2测量的方法”,表示第五章第三节第二条的标题是“测量的方法”。
注意:同一层次各段内容是否列标题应一致,各层次的下一级序号标法应一致,若层次较少可不用若干加括号的序号。
二、正文中图、表、公式、算式等的序号
文中的图、表、公式、算式等序号一律用阿拉伯数字分别依序连续编排序号,其标注形式应便于互相区别,如“图1、表2、式(5)”等;对长篇研究报告也可以分章(条)依序编码,如“图2.1、表4.2、式(3.3)”等,其前一个数字表示章(条)序号,后一个数字表示本章中图表、公式的序号。
三、注释和参考文献的序号
文中注释极少量的可用“*”、“**”表示,一般用圆圈的阿拉伯数字依序标注,如“①、②、③……”,标在所注对象的右上角。页脚或文末注释中对于相同内容的注释条目可合并写,如“⑥⑨马斯洛,《存在心理学探索》,昆明:云南人民出版社,1987年,130、126页”。
参考文献的序号标注一般用方括号的阿拉伯数字,如“[1]、[2]、[3]……”,也有不加括号的。文末参考文献与文中内容对应的,应在相应文字的右上角依序标出序号。
四、附录序号
论文的附录序号一般用大写英文字母标示,如“附录A、附录B、附录C……”。附录中的图、表、式、参考文献等另行编序号,与正文分开,也一律用阿拉伯数字编码,但在数码前冠以附录序码,如:图A1、表B2、式(C3)、文献[D4]等。
五、页码序号
页码标注由正文的首页开始,作为第1页,可以标注在页眉或页脚的中间或右边。封面、封二、封三和封底不编入页码。可以将扉页、序、目次页等前置部分单独编排页码。各页页码应标注在相同位置。
二 : 数字信号处理论文
数字信号处理论文
摘要
随着计算机通信技术的迅速发展,尤其是Internet技术的发展,多媒体存储和传输技术的进步使存储和传输数字化信息成为可能,然而,这也使盗版者能以低廉的成本复制及传播未经授权的数字产品内容,出于对利益的考虑,数字产品的版权所有者迫切需要解决知识产权的保护问题。[www.61k.com]而数字水印正式在这一背景下提出的,是数字产权保护技术之一。本文介绍了数字水印的产生背景、基本原理、应用方面等,并分析了基于奇异值分解的数字水印技术。
关键词:数字水印;奇异值分解;版权保护
1. 数字水印研究的背景
信息媒体的数字化为信息的存取提供了极大的便利性,同时也显著提高了信息达的效率和准确性。特别是随着计算机网络通讯技术的发展,数据的交换和传输变了一个相对简单的过程,人们借助于计算机、数字扫描仪、打印机等电子设备可以便、迅速地将数字信息传输到所期望的地方。随之而来的副作用是这些数字形式的据文件或作品使有恶意的个人和团体有可能在没有得到作品所有者的许可下拷贝和播有版权的内容,例如,现代盗版者只需轻点几下鼠标就可以获得与原版一样的复品,并以此获取暴利;而一些具有特殊意义的信息,如涉及司法诉讼、政府机要等息,则会遭到恶意攻击和篡改伪造等等。这一系列数字化技术本身的可复制和广泛播的特性所带来的负面效应,.己成为信息产业健康持续发展的一大障碍。目前,数字媒体的信息安全、知识产权保护和认证问题变得日益突出,且已成为数字世界中一非常重要和紧迫的议题。
加密技术是防止数据非法复制的重要手段,它可以保证数据的安全传输,但仅仅依靠密码技术并不能彻底解决数据的非授权复制问题。这是因为加密数据在检查和使用之前,必须进行解密,任何不遵守版权契约的使用者均可对解密后的数据进行任何形式的传播。如果数据的预定接受者不只一个,那么就无法保证某些合法用户不将数据传送给非法用户。
90年代初开始,针对上述方法的缺陷,_种新的版权保护技术一数字水印
数字信号处理论文 数字信号处理论文
(Digital Watermarking)技术出现了,它是一种综合信号处理、数字通信、密码学、计算机网络等多学科的新兴技术。(www.61k.com)它通过一定的算法将一些标志性信息(这些标志可以是作者的序列号,公司的标志,有特殊意义的文本等,可以用来识别数据的拥有权),直接嵌入到多媒体数据中,但不影响原数据的价值和使用,并且不能被人的知觉系统所察觉或注意到,只有通过专门的检测器或阅读器才能提取。与加密技术不同,数字水印技术旨在对数字媒体提供有效的内容保护,弥补数字加密技术的不足,它并不能阻止盗版活动的发生,但它可以判别对象是否受到保护,监视被保护数据的传播、真伪鉴别和非法拷贝,解决版权纠纷并提供证据。成为多媒体数据保护领域里最重要、最行之有效的方法之一。
2. 数字水印简介
数字水印(Digital Watermarking)技术是将一些标识信息(即数字水印)直接嵌入数字载体(包括多媒体、文档、软件等)当中,但不影响原载体的使用价值,也不容易被人的知觉系统(如视觉或听觉系统)觉察或注意到。通过这些隐藏在载体中的信息,可以达到确认内容创建者、购买者、传送隐秘信息或者判断载体是否被篡改等目的。数字水印是信息隐藏技术的一个重要研究方向。
数字水印是一种有效的数字产品版权保护和数据安全维护技术,是信息隐藏技术研究领域的一个重要分支。它将具有特定意义的标记(水印),利用数字嵌入的方法隐藏在数字图像,声音,文档,图书,视频等数字产品中,用以证明创作者对其作品的所有权,并作为鉴定,起诉非法侵权行为的证据,同时通过对水印的检测和分析来保证数字信息的完整性可靠性,从而成为知识产权保护和数字多媒体防伪的有效手段。数字水印一般具有如下特点:
? 可证明性:水印应能为受到版权保护的信息产品的归属提供完全可靠的证
据。水印算法能够将所有者的有关信息(如注册的用户号码、产品标志或有意义的文字等)嵌入到被保护的对象中,并在需要的时候将这些信息提取出来。水印可以用来判别对象是否受到保护,并能够监视被保护数据的传播、真伪鉴别以及非法拷贝控制等。这际上也是发展水印技术的基本动力。
数字信号处理论文 数字信号处理论文
? 不可感知性:不可感知性是指视觉或听觉上的不可感知性,即指因嵌入水印
导致载体数据的变换对于观察者的视觉或听觉系统来讲应该是不可察觉的,最理想的情况是水印与原始载体在视觉上是一模一样的,这是绝大多数水印算法所应达到的要求。[www.61k.com)
? 稳健性:稳健性是指水印应该能够承受大量的物理和几何失真,包括有意的
(如恶意攻击)或无意的(如图像压缩、滤波、打印、扫描与复印、噪声污染、尺寸变换等等)。显然在经过这些操作后,稳健的水印算法应仍能从水印载体中提取出嵌入的水印或证明水印的存在。一个鲁棒的水印应做到若攻击者实图删除水印将会导致水印载体的彻底破坏。
3. 数字水印的基本原理
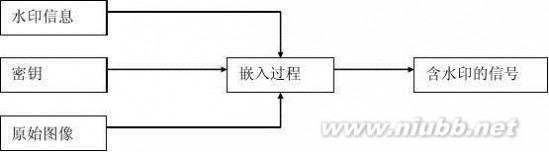
数字水印技术是通过一定的算法将一些标志性信息直接嵌到多媒体内容中,目前大多数水印制作方案都采用密码学中的加密(包括公开密钥、私有密钥)体系来加强,在水印的嵌入,提取时采用一种密钥,甚至几种密钥的联合使用。水印的嵌入和提取方法如图1、图2所示:
图1 数字水印嵌入过程
水印嵌入过程中,首先要产生水印。要嵌入的信息可以是各种性质的,如随机序列、数字、图像、文本等。密钥是用来增强安全性的,可以防止未经授权者读取信息。水印嵌入过程的输出是嵌入了水印的图像。
数字信号处理论文 数字信号处理论文
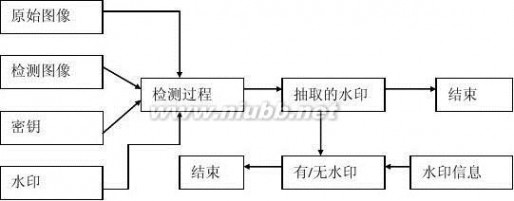
图2 数字水印检测/抽取过程
水印检测过程的输入是被测试的图像,它可能是没有嵌入水印的,也可能是嵌入了水印后又被攻击的图像。(www.61k.com)由于不同的水印算法,水印检测的输入还可能包含密钥、原始图像等。水印检测过程的输出或是检测出的水印,或是一个关于水印是否存在于被检测的信号的置信度值。图2中,水印检测时若不需要原始水印及原始载体图像,则水印为盲水印,否则为非盲水印。
4. 数字水印的实现
数字水印可以分为空间域数字水印和变换域数字水印两大类实现。
较早的数字水印算法从本质上来说都是空间域上的,通过改变某些象素的灰度将要隐蔽的信息嵌入其中,将数字水印直接加载在数据上。空间域方法具有算法简单、速度快、容易实现的优点。特别是它几乎可以无损的恢复载体图象和水印信息,这对于某些应用是必要的,可以细分为如下几种方法:
(1)最低有效位法,该方法就是利用原始数据的最低几位来隐蔽信息的,具体取多少位以人的听觉或视觉系统无法察觉为原则。
(2)Patchwork方法及纹理映射编码方法,该方法是通过任意选择N对图象点,增加一点亮度的同时,降低相应另一点的亮度值来加载数字水印。
(3)文档结构微调方法,在通用文档图象(postscript)中隐藏特定二进制信息的技术,主要是通过垂直移动行距,水平调整字距,调整文字特性等来完成编码。
基于变换域的技术可以嵌入大量比特的数据而不会导致不可察觉的缺陷,往往通过改变频域的一些系数的值,采用类似扩频图象的技术来隐藏数字水印信息。这类技术一般基于常用的图象变换,基于局部或全部的变换,这些变换包括
数字信号处理论文 数字信号处理论文
离散余弦变换(DCT)、小波变换(WT)、付氏变换(FT或FFT)以及哈达马变换(Hadamard Transform)等等。[www.61k.com]其中基于分块的DCT是最常用的变换之一。频域方法具有如下优点:
(1)在频域中嵌入的水印的信号能量可以分布到所有的象素上,有利于保证水印的不可见性;
(2)在频域中可以利用人类视觉系统的某些特性,可以更方便、更有效的进行水印的编码。不过,频域变换和反变换过程中是有损的,同时其运算量也很大,对一些精确或快速应用的场合不太适合。目前常用的方法有平面隐藏法和基于DCT或DFT的系数隐藏法。
5. 数字水印的应用及发展
由于数字水印技术与传统技术手段相比有诸多的优点,使得水印技术有很广的应用需求,为企业和客户提供了很多的商业机会。根据水印技术的功能,可以将数字水印的应用领域归纳为以下几类:
(1)数字作品的版权保护
数字作品的版权保护是数字水印技术最重要的应用方面。它的目标是嵌入有关数据来源的信息,典型的是数据的版权拥有者的特有标识,以阻止他人声明数据的版权。 “数字水印"利用数据隐藏原理使版权标志不可见或不可听,既不损害原作品,又达到了版权保护的目的。这一应用的主要驱动力来自互联网,那里有成百上千万的图像可以免费获得,而合法的拥有者却想要保护自己的版权。目前,用于版权保护的数字水印技术已经进入了初步实用化阶段,IBM公司在其“数字图书馆"软件中就提供了数字水印功能,Adobe公司也在其著名的Photoshop软件中集成了Digimarc公司的数字水印插件。然而实事求是地说,目前市场上的数字水印产品在技术上还不成熟,很容易被破坏或破解,距离真正的实用还有很长的路要走。
(2)商务交易中的票据防伪
随着高质量图像输入输出设备的发展,特别是精度超过1200dpi的彩色喷墨、激光打印机和高精度彩色复印机的出现,使得货币、支票以及其他票据的伪造变得更加容易。数字水印技术可以为各种票据提供不可见的认证标志,从而大大增加了伪造的 数字水印正处在迅速发展的过程中,掌握其发展方向对指导数字水印的研究有着重要的意义,我们认为今后数字水印的技术研究将侧重于完善数字水印理论、提高数字水印算法的稳健性、安全性、研究其在实际网络中的应用及建立相关标准等方面。在网络信息技术迅速发展的今天,数字水印技术的研究
数字信号处理论文 数字信号处理论文
具有明显的意义,数字水印技术将对保护各种形式的数字产品起到重要的作用,但必须认识到数字水印技术并非万能的,必须配合密码学技术及认证技术、数字签名或者数字信封等技术一起使用。(www.61k.com)一个实用的数字水印方案必须有这些技术的配合才能抵抗各种攻击,构成完整的数字产品版权保护解决方案。
(3)真实性验证
数字水印能够验证文档的真实性,这一特性使得数字水印技术可应用于电子商务和多媒体信息分发领域。如可以在身份证、信用卡、AI'M取款卡、银行支票、个人支票中嵌入水印信息用于防伪;在静态图像和视频中嵌入创建时间和创建的设备标识,当扫描仪、打印机、影印机或刻录机发现要拷贝的文档中没有对图像或视频的扫描、打印、拷贝权限时,它们就会拒绝用户进行这些操作。
(4)篡改提示
当数字作品被用于法庭、医学、新闻及商业时,常需要确定它们的内容是否被修改、伪造或特殊处理过。为实现该目的通常将原始图像分成多个独立的块,每个块加入不同的水印。为确定其完整性,可通过检测每个数据块中的水印信号,可确定作品的完整性。与其它水印不同的是,这类水印必须是脆弱的,并且检测水印信号时,不需要原始数据。
(5)完整性认证
传统的基于数字签名信息的完整性认证系统一般将签名与媒体信息捆绑在一起存储或传输,由于签名独立于媒体数据存在,这样既占用一定的存储空间或信道带宽,又很容易被删除。而基于数字水印的认证系统则将水印内嵌于媒体信息中,水印无需占用存储空间或信道带宽,且很难被除去:再者,数字水印技术还可以采用双水印系统(即脆弱性水印与鲁棒性水印相结合)对数字产品进行多重目的的保护。在当今信息认证领域中,数字水印技术因其具有广阔的应用前景而日益为学术界和商业界所关注。
随着数字水印技术的发展,数字水印的应用领域也得到了扩展,数字水印的基本应用领域是版权保护、隐藏标识、认证和安全不可见通信。当数字水印应用于版权保护时,潜在的应用市场在于电子商务、在线或离线地分发多媒体内容以及大规模的广播服务。数字水印用于隐藏标识时,可在医学、制图、数字成像、数字图像监控、多媒体索引和基于内容的检索等领域得到应用。数字水印的认证方面主要ID卡、信用卡、ATM卡等上面数字水印的安全不可见通信将在国防和情报部门得到广泛的应用。
6. 基于奇异值分解的数字水印
数字信号处理论文 数字信号处理论文
6.1 基本原理分析
定义1 对于N?N矩阵A,有N个标量?i(i?1,2,?,N)满足:
A??iI?0
则称这一组?i为矩阵A唯一的特征值.
定义2 如果存在这样一个N?1的向量Vi,有:
AVi??iVi
则称Vi为A的与特征值?i对应的一个特征向量. A一共有N个特征向量.
定义3 (矩阵奇异值分解) 矩阵的奇异值分解(Singular Value
Decomposition,简称SVD)是矩阵所固有的特征,设矩阵A?Rm?n,
rank(A)?r,r?n,那么矩阵A
的奇异值分解定义如下:
??10?0???
?[u1,u2,?,um]?
????00??r??
r
A?UDV
T
[v1,v2,?,vn]?
m?n
T
??
j?1
j
ujvj
m?mn?n
U?[u1,?um]?R其中,和V?[v1,?vn]?R是正交矩阵,其列向量分别为ui和
vi;U,V分别称为矩阵A的左奇异矩阵和右奇异矩阵;D是对角阵;?i(i?1,?,r)
称作矩阵A的奇异值,此处是AAT或ATA的特征值?i的正平方根,满足
?1??2????r??r?
1
??
??m?0。[www.61k.com)矩阵奇异值具有很好的稳定性,当矩阵A
有微小振动时,其奇异值的改变不会大于振动矩阵的2-范数。若矩阵奇异值经过归一化处理,则可实现奇异值的比例不变性。另外,矩阵奇异值还具有旋转不变性,因此,奇异值能有效地反映矩阵的特征,在图像处理中能表现图像的代数特性。矩阵SVD分解在一定程度上可以用来进行图像压缩.对于图像分解得到的奇异值矩阵?,将其较小的一些对角元清为0,再进行SVD反变换即可完成图像的有损压缩.
数字信号处理论文 数字信号处理论文
SVD方法的基本原理是将水印嵌入到图像矩阵的奇异值中。(www.61k.com)在水印的嵌人过程中对图像矩阵Am?n的奇异值分解,得到两个正交矩阵U、V及一个对角阵S。
水印W?Rn?n 被叠加到矩阵S上,对新产生的矩阵S??W进行奇异值分解,得
T到U1、S1和V1(S??W?U1S1V1),其中常数??0调节水印的叠加强度。然后将
矩阵U、S1和VT 相乘,得到处理后的包含水印的图像A 。即如果矩阵A和W 分别表示原始图像矩阵和水印,那么通过以下的四个步骤得到水印图 A:
1) 将图像矩阵A进行奇异值分解
A?USVT??
2) 读取水印图像W,将其迭加到对角阵S上得到新矩阵S'
S?S??W'
3) 将新矩阵S'进行奇异值分解
S?U1S1V1'T
4)得到含水印的图像
?
A?US1VT
V1 和可能损坏的水印图像A*,在水印的检测过程中,如果给出矩阵U1 、S、
那么通过简单的逆过程就可以提取出可能已经失真的水印 W*,即:
1) 可能损坏的水印图像A*进行奇异值分解
A?US1V****T
2) 计算中间矩阵
D?U1S1V1**T
3) 获得水印图像
数字信号处理论文 数字信号处理论文
*W?1
?(D?S) *
计算提取的水印与原水印的相似系数,作为二者的相似程度, 相似系数越接近1就越相似。[www.61k.com)
6.2 Matlab仿真分析
Matlab程序:
I=imread('lena256.bmp'); %读入原图
II=im2double(I); %转化为[0,1)double型 %II为原图像
[m,n]=size(II); %原图像大小
af=0.1; %嵌入强度
[U,S,V]=svd(II); %进行奇异值分解
M=imread('logo.tif'); %读入水印图像
W=im2double(M); %转化为[0,1)double型
[m1,n1]=size(W);
WW=zeros(m,n);
for i=1:m1
for j=1:n1
WW(i,j)=W(i,j);
end
end
S1=S+af*WW;%加入水印后的对角阵
[U1,SS,V1]=svd(S1); %再进行奇异值分解
CWI=U*SS*V'; %嵌入水印后图像
数字信号处理论文 数字信号处理论文
subplot(2,2,1); imshow(II); title('原图像'); %显示原图像
subplot(2,2,2); imshow(CWI); title('嵌入了水印后图像');%显示嵌入了水印后图像 %提取水印
NCWI=zeros(size(CWI));
AA=randn(size(CWI));
NCWI=CWI+AA*0.01; %对含水印的图像加噪声
[UU,S2,VV]=svd(NCWI); %对含有水印的图像进行奇异值分解
SN=U1*S2*V1'; %计算中间矩阵
WN=(SN-S)/af; %提取水印
WNN=zeros(m1,n1);
for i=1:m1
for j=1:n1
WNN(i,j)=WN(i,j);
end
end
subplot(2,2,3);imshow(W); title('原始的水印');
subplot(2,2,4);imshow(WNN); title('提取的水印');
NC=corrcoef(W,WNN);
nc=NC(1,2);
fprintf('原始水印和提取水印的相关系数:%5.4f\n',nc);
6.3 实验结果
数字信号处理论文 数字信号处理论文

图3 水印对比图
7. 总结与展望
数字水印作为一门崭新的版权保护技术,其诞生至今不过数十年,但目前无论是在国内还是在国外,都已经成了一个研究热点。[www.61k.com]不但有大量的论文问世,多次大型会议召开,不少研究机构已经开始研究数字水印的实用性问题了。我国也在此领域投入了大量的人力物力,并已经取得了一些成果。但是无论是国内还是国外,都应该看到数字水印发展的不足。数字水印技术解决了数字产品的版权问题,本论文就数字水印的算法进行了研究,并将混沌理论引入了水印技术,主要完成了以下工作:对数字水印技术研究的背景做了详细分析;给出了数字水印的基本原理;列举现有数字水印实现的算法;最后就是对基于奇异值分解的数字水印技术进行了详细的分析和仿真说明。
数字水印技术作为一种新兴的应用技术,一个尚未完善的科学技术领域,在对研究学者提出严峻挑战的同时,也带来了难得的机遇,因为在一种理论及技术趋于成熟的阶段,正是各种观点百家争鸣的时候,面对这样一个开放的研究体系,真正的突破者往往属于勇往直前、积极探索的先行者。
数字信号处理论文 数字信号处理论文
参考文献
[1] 姚天任,孙洪.现代数字信号处理.武汉:华中科技大学出版社,1999.
[2] 孙圣和,陆哲明等.数字水印技术及应用[M].北京:科学出版社,2004.
[3] 伯晓晨,沈林成,常文森.数字水印技术:概念、应用及现状[J].计算机世界,2000,1(3):
1-4.
[4] 张春田,苏育挺,管晓康。(www.61k.com]多媒体数字水印技术[J].通讯学报,2000,21(9):46-52.
[5] E.Koch, www.61k.com Robust and Hidden Image Copyright Labeling[J].Proc.of
IEEE Workshop on Nonlinear Signal and Image Processing,1995,452-455.
[6] I.J.Cox,J.Killan,T.Leighton et al.A secure,robust watermark for
multimedia[C].In Workshop on information hiding, Cambrige,UK,Number 1174 in lecture notes on computer science.Springer-Verlag.1996,185-246.
[7] I.Pitas.A method for watermark casting on digital images[J].IEEE www.61k.com
Circuits and Systems for Video Technology,1998,8(6):775-780.
[8] A.Piva,M.Barni and www.61k.com protection of digitial images by
means of frequency domian watermarking[C].In Proceedings of SPIE,vol.3456,1998,25-35.
[9] Chandra D V S.Digital image watermarking using singular value
decomposition[A].In:proceedings of 45th IEEE Midest Symposium on Circuits and Systems[C],Tulsa,OK,USA,2002,246-267.
[10] 汪小帆,戴乐伟,茅耀斌.信息隐藏技术方法与应用(第一版)[M].北京:机械工
业出版社,2001.18.
三 : 数字信号处理期末论文15
题 目: 基于DSP的FFT程序设计的研究
作 者
系 别
指导老师
完成时间 2013.06 届 别 专 业 职 称
内容摘要
快速傅里叶变 (Fas Fourier Tranformation,FFT)是将一个大点数N的DFT分解为若干小点的D F T的组合。将用运算工作量明显降低, 从而大大提高 离散傅里叶变换(D F T) 的计算速度。因各个科学技术领域广泛的使用了FFT 技术它大大推动了信号处理技术的进步,现已成为数字信号处理强有力的工具,本论文将比较全面的叙述各种快速傅里叶变换算法原理、特点,并完成了基于MATLAB的实现。
关键词:频谱分析;数字信号处理;MATLAB;DSP281x
引言:
1965年,库利(J.W.Cooley)和图基(J.W.Tukey)在《计算数学》杂志上发表了“机器计算傅立叶级数的一种算法”的文章,这是一篇关于计算DFT的一种快速有效的计算方法的文章。它的思路建立在对DFT运算内在规律的认识之上。这篇文章的发表使DFT的计算量大大减少,并导致了许多计算方法的发现。这些算法统称为快速傅立叶变换(Fast Fourier Transform),简称FFT,1984年,法国的杜哈梅尔(P.Dohamel)和霍尔曼(H.Hollmann)提出的分裂基快速算法,使运算效率进一步提高。FFT即为快速傅氏变换,是离散傅氏变换的快速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。它对傅氏变换的理论并没有新的发现,但是对于在计算机系统或者说数字系统中应用离散傅立叶变换,可以说是进了一大步。
随着科学的进步,FFT算法的重要意义已经远远超过傅里叶分析本身的应用。FFT算法之所以快速,其根本原因在于原始变化矩阵的多余行,此特性也适用于傅里叶变换外的其他一些正交变换,例如,快速沃尔什变换、数论变换等等。在FFT的影响下,人们对于广义的快速正交变换进行了深入研究,使各种快速变换在数字信号处理中占据了重要地位。因此说FFT对数字信号处理技术的发展起了重大推动作用。
信号处理中和频谱分析最为密切的理论基础是傅立叶变换(Fouriertransform,FT)。快速傅立叶变换(FFT)和数字滤波是数字信号处理的基本内容。信号时域采样理论实现了信号时域的离散化,而离散傅里叶变换理论实现了频域离散化,因而开辟了数字技术在频域处理信 号的新途径,推进了信号的频谱分析技术向更广的领域发展。
1.信号的频谱分析
如果信号频域是离散的,则信号在时域就表现为周期性的时间函数;相反信号在时域上是离 散的,则该信号在频域必然表现为周期的频率函数。不难设想,一个离散周期序列,它一定 具有既是周期又是离散的频谱。有限长序列的离散傅里叶变换和周期序列的离散傅里叶级数 本质是一样的。因而有限长序列的离散傅里叶变换的定义为:x(n)和X(k)是一个有限长序列的离散傅里叶变换对。
式(1.1)为x(n)的N点离散傅里叶变换(DFT),式(1.2)为X(k)的N点离散傅里叶反变换(IDFT)。
作为有限长序列的一种傅里叶表示法,离散傅里叶变换除了在理论上相当重要之外,而且由 于存在有效的快速算法—快速离散傅里叶变换(FFT),因而在各种数字信号处理的算法中起着核心作用。快速傅里叶变换是指1965年库力和图基(Cooley-Tukey)算法为基础的一类高 效算法,它的出现和发展对推动信号的数字处理技术的变革和发展起着重大作用。
信号谱分析是数字信号处理的重要内容,对确定的信号其时 域表示是确定的,其频谱可以通 过傅立叶变换得到。但在实际应用中,携带信息的信号本质上都是随机的,随机信号不能用 确定的时间函数表示,只能用概率分布函数、概率密度函数或统计平均特性来描述。通常把 随机信号看作无限长度和无限能量的功率信号,由于不满足绝对可积,其傅立叶变换不存在 ,因此只能研究其功率在频域的分布,即功率谱或功率谱密度。实际应用中人们所能得到的 随机信号的样本函数总是有限长序列,根据有限长度的信号所得的功率谱只是随机信号真实 功率谱的估计,称为功率谱估计。功率谱是平稳随机信号在频域上,描述各频率分量功率分 布情况的基本特征量,由于功率谱与相关函数之间是一对傅立叶变换,经典功率谱估计都依 据DFT,而采用FFT算法,故称之为非参数方法。若间接使用有限数据先估计相关函数,进而 求出功率谱的估计,为自相关法。
2. 利用MATLAB进行随机信号功率谱分析
MATLAB在DSP(数字信号处理)中有着广泛的应用。例如:MATLAB的信号处理工具箱、滤波 器设计工具箱以及Simulink的建模仿真功能,还有针对DSP系统的专用数据库——DSP模块库 和定点DSP模块库。此外,信号处理工具SPTool(Signalprocessingtool)提供了一个于 完成信号处理任务的GUI集成环境。利用他可以从MATLAB工作空间或者文件直接导入已经设 计好的信号、滤波器或频谱;可以分析、聆听和输出时域信号;可以
设计、分析和输出滤波 器;可以完成对信号的滤波;可以对输入输出信号进行各种谱分析并输出结果,等等。
在下面的程序中利用MATLAB分信号频域的幅度谱、相位谱、功率谱。通过
对频谱图的比较, 观察出信号的频域特征。
3. 利用DSP进行随机信号功率谱分析
对信号的数字处理,是利用计算机或专用的数字设备对信号进行采集、变换、滤波、估值、 增强、压缩和识别等加工处理,以得到符合人们需要的信号形式并进行有效的传输与应用。 数字信号处理器,也称DSP芯片,是一种专门用于数字信号处理的微处理器。DSP芯片的内部采用程序和数据分开的哈佛结构,具有专门的硬件乘法器,广泛采用流水线操作,提供特殊 的DSP指令,可以用来快速地实现各种数字信号处理算法。
基2的FFT硬件实现有多种形式,其工作原理主要采用:①顺序处理;②级联处理;③并 行迭代处理;④阵列处理等。
4.matlab结果比较
(1).自编FFT程序与MATLAB调用FFT程序比较
6
4
2
00246810121416
6
4
2
00246810121416
自编函数与调用fft函数结果是一致的。
(2).自编产生多频信号程序及多频信号时序图和调用MATLAB自带FFT程序处理此多频信号及频谱分析图
数字信号处理期末论文15_dsp论文
多频信号
12000
10000
8000
6000
4000
2000
-20000246810121416
184频谱
16
14
12
10
8
6
4
2
5.结论
文章通过对随机信号的功率谱分析,了解信号中的频谱组成,进而对信号特征进行考察。完 成了基于MATLAB的信号在时域和频域的波形仿真。
在CCS环境下,利用汇编语言实现FFT算法和功率谱的估计,通过CCS所包含的画图函数进行相应的频谱观测,最后,通过仿真器在硬件DSP281x上实现了随机信号的功率谱分析。
参考文献
[1] 陈后金,薛健,胡健.数字信号处理[M].北京:高等教育出版社,2004.
[2] 董长虹,余啸海,高成,金涛.MATLAB信号处理与应用[M].北京:国防工业 出版社,2005.
[3] 梁虹,梁洁,陈跃斌.信号与系统分析及MATLAB实现[M].北京:电子工业出 版社,2002.
[4] 张志涌.精通MATLAB6.5版[M].北京:北京航空航天大学出版社,2003.
[5] 彭启琮,李玉柏,管庆.DSP技术的发展与应用[M].北京:高等教育出版社, 2002.
附录1:在利用DSP进行频谱分析的程序设计中,实现的主要程序为:
STM#fft-data,AR2
STM#fft-data,AR3
STM#fft-out,AR4
STM#K-FFT-SIZE*2-1,BRC
RPTBpower-end-1
SQUR*AR2+,A
SQURA*AR2+,A
STHA,*AR4+13-6-18 基于DSP的信号频谱分析与实现
DSP281x
产生一个多频信号,分析其频谱,并和matlab结果比较
FFT程序设计
#include "DSP281x_Device.h" // DSP281x Headerfile Include File
#include "DSP281x_Examples.h" // DSP281x Examples Include File
#include "f2812a.h"
#include"math.h"
#define PI 3.1415926
#define SAMPLENUMBER 128
void InitForFFT();
void MakeWave();
//void FFT(float dataR[SAMPLENUMBER],float dataI[SAMPLENUMBER]);
int INPUT[SAMPLENUMBER],DATA[SAMPLENUMBER];
float fWaveR[SAMPLENUMBER],fWaveI[SAMPLENUMBER],w[SAMPLENUMBER];
float sin_tab[SAMPLENUMBER],cos_tab[SAMPLENUMBER];
void FFT(float dataR[SAMPLENUMBER],float dataI[SAMPLENUMBER])
{
int x0,x1,x2,x3,x4,x5,x6,xx;
int i,j,k,b,p,L;
float TR,TI,temp;
for ( i=0;i<SAMPLENUMBER;i++ )
{
x0=x1=x2=x3=x4=x5=x6=0;
x0=i&0x01; x1=(i/2)&0x01; x2=(i/4)&0x01; x3=(i/8)&0x01;x4=(i/16)&0x01; x5=(i/32)&0x01; x6=(i/64)&0x01;
xx=x0*64+x1*32+x2*16+x3*8+x4*4+x5*2+x6;
dataI[xx]=dataR[i];
}
for ( i=0;i<SAMPLENUMBER;i++ )
{
dataR[i]=dataI[i]; dataI[i]=0;
}
for ( L=1;L<=7;L++ )
{ /* for(1) */
b=1; i=L-1;
while ( i>0 )
{
b=b*2; i--;
} /* b= 2^(L-1) */
for ( j=0;j<=b-1;j++ ) /* for (2) */
{
p=1; i=7-L;
while ( i>0 ) /* p=pow(2,7-L)*j; */
{
p=p*2; i--;
}
p=p*j;
for ( k=j;k<128;k=k+2*b ) /* for (3) */
{
TR=dataR[k]; TI=dataI[k]; temp=dataR[k+b];
dataR[k]=dataR[k]+dataR[k+b]*cos_tab[p]+dataI[k+b]*sin_tab[p]; dataI[k]=dataI[k]-dataR[k+b]*sin_tab[p]+dataI[k+b]*cos_tab[p]; dataR[k+b]=TR-dataR[k+b]*cos_tab[p]-dataI[k+b]*sin_tab[p]; dataI[k+b]=TI+temp*sin_tab[p]-dataI[k+b]*cos_tab[p]; } /* END for (3) */
} /* END for (2) */
} /* END for (1) */
for ( i=0;i<SAMPLENUMBER/2;i++ )
{
w[i]=sqrt(dataR[i]*dataR[i]+dataI[i]*dataI[i]);
}
} /* END FFT */
main()
{
int i;
InitForFFT();
MakeWave();
for ( i=0;i<SAMPLENUMBER;i++ )
{
fWaveR[i]=INPUT[i];
fWaveI[i]=0.0f;
w[i]=0.0f;
}
FFT(fWaveR,fWaveI);
for ( i=0;i<SAMPLENUMBER;i++ )
{
DATA[i]=w[i];
}
while ( 1 ); // break point
}
void InitForFFT()
{
int i;
for ( i=0;i<SAMPLENUMBER;i++ )
{
sin_tab[i]=sin(PI*2*i/SAMPLENUMBER);
cos_tab[i]=cos(PI*2*i/SAMPLENUMBER);
}
}
void MakeWave()
{
int i;
for ( i=0;i<SAMPLENUMBER;i++ )
{
INPUT[i]=sin(PI*2*i/SAMPLENUMBER*3)*1024; }
}
附录2:MATLAB调用FFT程序
x=randn(1,16)
s=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
for k=1:16
for n=1:16
s(k)=s(k)+x(n).*2.718^(-(j*2*pi*k*n)/16)
end
end
subplot(2,1,1), stem(abs(s))
y=fft(x)
subplot(2,1,2), stem(abs(y))
附录3:调用MATLAB自带FFT程序处理此多频信号及频谱分析图 a=0
t=1:0.1:16
for f=1:128
a=a+1024*sin(2*3.14*f*3*t/128)
end
figure,plot(t,a)
title('多频信号')
y=fft(a)
figure,plot(abs(y))
title('频谱')
本文标题:数字信号处理论文-论文数字序号的使用61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1