一 : 圆其说

圆其说

夏夜辗转无眠于床上，却不是因为失眠于斯，而是小区绿化带中的蛙鸣，亦不是受蛙鸣所困，而是我实在舍不得这漫天倘佯的奏鸣！我忖度着——这青蛙们都该是些惊蛰不久的小生命吧！

对，小生命，和多年前受我迫害至死的青蛙一样，都还是小得可怜的生命。

那是二十年前的夏天，我在乡间的路上遇见了一只青蛙，青丝细雨之下，我用一枝树桠结束了它短暂的生命——对着它雪白的肚皮，毫不犹豫地以一种叫现在的我咋舌不已的戾气迫害死了那只青蛙。而我对自己昔日那个残忍的举动，有了一个合理的辩护——都是年少无知惹下的祸害嘛！一个十来岁的娃娃，哪里懂得什么生命的平衡至理啊。而思忆起如今屠杀蛙类不止的商贩之举为，他们却远不满足于“年少”的条件，却也同样有着以此一般无知且“合理”的掩饰——都是为了顾客的朵颐着想啊！

我为剥夺那只青蛙的生命找到了庇护港，屠夫也对此有着不让的借口供以自危，这都是无知惹的祸。而青蛙呢？我反诘道自己。它们也是一样无知吗？平日里一个个的不是叫嚷得不知道比谁都要大声吗，临死了，怎么还学会了用沉默掩饰恐惧的挣扎！就连这低能些的生物，都在与我们一起循环于这自我不断掩饰的怪圈之中吗？

我想，这怪圈还不只一个。( 文章阅读网：www.61k.com )

历史仿佛在无限的空间内循环着极为有限的变动。

那是十岁的我，永远地离开了我的外婆，不对，是我的外婆，在我十岁的时候，永远地离开了我。（现在想来，语法上的这些对或错，又能改变些什么呢？）外婆入棺下葬那天，恰好我也在场，我是目送着她的棺材一尺一尺地降入到墓地的，和人出生时一寸一寸地来到这个世界上是一样的感觉——比起一尺一尺，一寸一寸显然是个更为冗长的过程；而比起一寸一寸，一尺一尺显然是一种更为猛烈快速的疼痛。我可以想像，比起死，生是一个更为漫长的隐痛过程，也不反对有人说比起生，死是一个迅疾的剧痛过程。可是谁又会说生或死都是个不大痛苦的事儿呢？

是的，我和外婆之间这些或隐或烈、或长或短的痛楚，我原以为都是归我一人承受的，直到上个月末，母亲离开了她两岁的小外孙，搬来与我同住，在他们二人离别的那一刻，又叫我警惕住了不小的动静——原来“痛苦”二字素来都不是一个可数名词，你永远都不知道它还有多少未及，你也永远不清楚它会何时再次降临，所以那些说着“我要替你承担一切（一辈子）痛苦”的人，也都是条不小的糊涂虫吧！我不能说我的母亲对这养育两年的小家伙没有甚浓的情感，也不可以说我这个涉世不深的小侄子丝毫感受不到裁剪而断的情线，痛苦，总不单是个体生命的事儿。

这便又是囿于那个怪圈中的怪迹——在无限的历史空间之内，轮回毕露着不断掩饰自身疲敝的人、循环播放着骨肉别离的电影。

可还有什么东西可以不囿于此的？我呆望着眼前卧室窗台上的金鱼缸，那些个在极其有限的空间之内的金鱼，都是只有七秒钟的记忆的（姑且这样掩饰道吧！），每过七秒钟，这些金鱼的眼中便会渐次出现“不同别样”的风景，这便是无限的可能吧！终于让我找到了一个不囿于上述怪圈的生命体，这让我鼓足了十二分的勇气——我要换鱼缸，我要换一个更大的鱼缸，我要不间断地在这个“大的鱼缸”之前加上一个“更”字，从明天起，我要开始为这几条金鱼寻找一个更加广阔，而至无限的空间——我要把它们放生到无限空间的大自然中去，在无限的空间之内，它们亦有无限的记忆，它们可以不再囿于什么“有限”的怪圈之内！

我对此身觉欢畅不已——我可以创造出生物界的奇迹了！怀揣着的这个梦想，它伴我穿透了整个黑夜，直到被那声猛烈的碎声刺破......

我起身四顾，发现母亲把她的小外孙从不远的姐姐家里接了过来打算小住几天，聊戚一番，可年幼的小侄子趁母亲一不留神，打碎了我窗台前的金鱼缸，散落一地的金鱼折腾鱼跃着，我一番以“猎奇”为掩饰，实则怀以私心想霸占金鱼之美的恶贯，也一并被这几条小鱼给搅得零碎不堪，金鱼们在地上痛哭地挣扎，我在床沿边为这金鱼痛苦不堪的命运怜痛着。

我想我还是得自圆其说得好——只要我救起这垂死的金鱼，它们还是有机会重归大自然的！它们可以在无限的空间内创造出无限的可能——它们可以不囿于任何怪圈，不囿于空间的封闭、不囿于生死离别......不，它们不可能！

它们不可能不去面对彼此的死亡与别离，就像我掩饰不住一己猎奇私心一样，它们也都掩饰不住失去水源的痛苦，奋力挣扎着......

这些，这些都是，这些都是些无法掩饰且无力抗拒的痛苦，若这都是某个生命体的单一命运也就罢了......

“儿子，你快些把那些掉在地上的金鱼救起来啊，再不动手，它们就死了！”厨房中的母亲闻声而来道。

“不大干系了！它们迟早都得死！”

“哎哟，我的小外孙啊，你也是的，叫你不要乱动你偏不听，这下好了吧，把舅舅惹伤心了吧！过两天就让你妈妈接你回去......”母亲一阵恍惚之中，接不住自己不已的话茬，惆怅于厨房门前的油烟朦胧之中。

二 : 椭圆及其标准方程A是圆X2+Y2=36上的任意一点，AB垂直X轴

椭圆及其标准方程

A 是圆X2+Y2=36上的任意一点，AB垂直X轴于B，以A为圆心，|AB|为半径的圆交圆于C、D，连接C、D交AB于P，当A在圆上时，求P点的轨迹方程

---

设A（a,b），P（x,y）,则

⊙A的方程（x-a）^2+(y-b)^2=b^2……①,⊙O的方程x^2+y^2=36……②

②-①得公弦CD的方程:2ax+2by=36+a^2

∵x=a时,y∈CD,代入上式得, 2by=36-a^2=b^2 ,∴y=b/2

把a=x,b=2y代入②得x^2+4y^2=36

∴P点的轨迹方程为(x^2)/36+(y^2)/9=1

三 : 椭圆及其标准方程

x2y21＝1的焦点坐标是( ) 25169

A．(±5,0) B．(0，±5)

C．(0，±12) D．(±12,0)

解析：c2＝a2－b2＝169－25＝122，∴c＝12.

又焦点在y轴上，故焦点坐标为(0，±12)．

答案：C

42．设定点F1(0，－2)、F2(0,2)，动点P满足条件|PF1|＋|PF2|＝m＋m(m>0)，则点P的

轨迹是( )

A．椭圆

C．不存在

4解析：m＋≥m B．线段 D．椭圆或线段 4m4. m

44当m＋m＝4即m＝2时，点P轨迹为线段F1F2；当m＋m>4时，点P轨迹为以F1、

F2为焦点的椭圆．

答案：D x2y2

3．已知椭圆1上的一点P到椭圆一个焦点的距离为3，到另一焦点距离为7，m16

则m等于( )

A．10

C．15 B．5 D．25

解析：由椭圆定义知|PF1|＋|PF2|＝2a＝10，

∴a＝5，∴a2＝25，即m＝25.

答案：D

53?的椭圆的标准方程是 4．两个焦点的坐标分别为(－2,0)，(2,0)，并且经过点P?2??2

( )

x2y2

A.1 106

x2y2

＋1 925

44 y2x2B.＋1 106y2x2D.＝1 92544

解析：由椭圆定义知：2a＝?5＋2?2＋?－3?2?2??2??52?2＋?3?2＝310＋1010. ?2??2?22

∴a10.∴b＝a－c＝6.

答案：A

5．椭圆5x2－ky2＝5的一个焦点是(0,2)，那么k＝________.

y2

解析：椭圆方程可化为：x＋＝1， 5－k2

则a2，b2＝1，又c＝2， k

5∴－－1＝4，∴k＝－1. k

答案：－1

x2y26＋＝1的焦点为F1、F2，点P在椭圆上．若|PF1|＝4，则|PF2|＝________，92

∠F1PF2的大小为________．

解析：由题意，a＝3，则|PF2|＝2a－|PF1|，

∴|PF2|＝2.在△F1PF2中，|PF1|＝4，|PF2|＝2，|F1F2|＝27，

|PF1|2＋|PF2|2－|F1F2|2

∴cos∠F1PF2＝2|PF1||PF2|

42＋22－?27?21＝ 22×4×2

∴∠F1PF2＝120°.

答案：2 120°

x227．点P为椭圆＋y＝1上一点，且∠F1PF2＝60°，求△F1PF2的面积． 4

解：由题意，a＝2，b＝1，c＝3，|PF1|＋|PF2|＝4.①

在△F1PF2中，|F1F2|2＝|PF1|2＋|PF2|2－2|PF1||PF2|cos 60°，

即12＝|PF1|2＋|PF2|2－|PF1||PF2|.②

①2得：|PF1|2＋|PF2|2＋2|PF1||PF2|＝16.③

4由②③得：|PF1||PF2|＝. 3

11433∴S△F1PF2＝|PF1||PF2|sin 60°＝×22323

8．求以椭圆9x2＋5y2＝45的焦点为焦点，且经过点M(26)的椭圆的标准方程．

x2y2

解：法一：方程9x＋5y＝45可化为＋1. 5922

则焦点是F1(0,2)，F2(0，－2)．

y2x2

设椭圆方程为1(a>b>0)， ab

∵M在椭圆上，∴2a＝|MF1|＋|MF2|

＝?2－0?2＋?6－2?2?2－0?2＋?6＋2?2 ＝(23－2)＋32)

＝43，

∴a＝3，即a2＝12.

∴b2＝a2－c2＝12－4＝8.

y2x2

∴椭圆的标准方程为1. 128

法二：由题知，焦点F1(0,2)，F2(0，－2)，则

y2x2

设所求椭圆方程为1(λ＞0)， λ＋4λ

64将x＝2，y＝6代入，得1， λ＋4λ

解得λ＝8，λ＝－2(舍去)．

y2x2

所求椭圆方程为1. 128

四 : 椭圆及其标准方程练习题

椭圆及其标准方程练习题

【基础知识】

一．椭圆的基本概念

1.椭圆的定义：我们把平面内与两个定点的距离的和等于常数 （

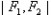
）的点

的轨迹叫做椭圆，用符号表示为这两个定点叫椭圆的 ，两个焦点之间的距离叫做椭圆的 。

椭圆方程的总形式为

[经典例题]：

例1. 根据定义推导椭圆标准方程.

已知B，C是两个定点，｜BC｜＝6，且?ABC的周长等于16，求顶点A

已知F1, F2是定点，| F1 F2|=8, 动点M满足|M F1|+|M F2|=8，则点M的轨迹是 （A）椭圆 （B）直线 （C）圆 （D）线段

1

例2.写出适合下列条件的椭圆的标准方程：

⑴两个焦点坐标分别是(-4,0)、（4，0），椭圆上一点P到两焦点的距离之和等于10；

⑵两个焦点坐标分别是（0，－2）和（0,2）且过（?

例3 求适合下列条件的椭圆的标准方程：

(1)两个焦点坐标分别是(-3，0)，(3，0)，椭圆经过点(5，0).

(2)两个焦点坐标分别是(0，5)，(0，-5)，椭圆上一点P到两焦点的距离和为26.

例4 已知椭圆经过两点（?

35,2235,)与(,) 22

例5 1.椭圆短轴长是2，长轴是短轴的2倍，则椭圆离心率是 ；

2.如果椭圆的焦距、短轴长、长轴长成等差数列，则其离心率为 ；

3.若椭圆的两个焦点F1、F2与短轴的一个端点B构成一个正三角形，则椭圆的离心率为 ；

[典型练习]： x2y2

??1上一点P到一个焦点的距离为5，则P到另一个焦点的距离为（ ） 椭圆259

?A.5 ?B.6 ?C.4 ?D.10

x2y2

??1的焦点坐标是（ ） 2.椭圆25169

?A.(±5，0)? B.(0，±5) ?C.(0，±12)? D.(±12，0)

x2y2

??1，焦点在x轴上，则其焦距为（ ） 3.已知椭圆的方程为8m2

?A.28?m2? B.222?m

?C.2m2?8? D.2m?22

4.a?6,c?1,焦点在y 2

x2y2

5. 椭圆??1的焦点坐标是 m?2m?5

（A）(±7, 0) （B）(0, ±7) （C）(±,0) （D）(0, ±7)

6．设F1,F2为定点，|F1F2|=6，动点M满足|MF1|?|MF2|?6，则动点M的轨迹是 （ ）

A.椭圆 B.直线 C.圆 D.线段?

x2y2

7.椭圆一直线过F1交椭圆于A、B两点，则?ABF2的周长为 （ ） ??1的左右焦点为F1,F2，167

A.32 B.16 C.8 D.4?

x2y2

??1上的一点，F1和F2是其焦点，若∠F1PF2=60°，则△F1PF2的面积为8. P为椭圆10064

9.如果方程x2?ky2?2表示焦点在y轴上的椭圆，则k的取值范围是______.

x2y2

??1表示焦点在y轴上的椭圆，则m的取值范围是______. 10.方程2mm?1

11.在△ABC中，BC=24，AC、AB的两条中线之和为39,求△ABC的重心轨迹方程.?

x2y2

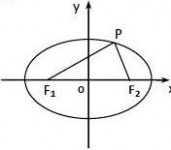
??1上，F1、F2是椭圆的焦点，且PF1⊥PF2，求 12. 已知点P在椭圆4924

（1）| PF1 |·| PF2 | （2）△PF1F2的面积

3

作业

1．判断下列方程是否表上椭圆，若是，求出a,b,c x2y2x2y2x2y2

①??1；②??1；③??1；④4y2?9x2?224242x2y2

椭圆??1的焦距是 ，焦点坐标为 ；若CD为过左焦点F1的弦，则?F2CD的169

3． 方程4x2?ky2?1的曲线是焦点在y上的椭圆 ，求k

x2y2

??1上一点P到焦点F1的距离等于6，则点P到另一个焦点F2的距离是 椭圆10036

动点P到两定点F1 (-4,0)，F2 (4,0)的距离的和是8，则动点P

6.平面内两个定点F1,F2之间的距离为2，一个动点M到这两个定点的距离和为6.建立适当的坐标系，推导出点M的轨迹方程.

4

本文标题：椭圆及其标准方程-圆其说
本文地址： http://www.61k.com/1170545.html