一 : 双曲线的离心率公式
双曲线的离心率公式
椭圆的离心率公式e=√1-(b/a)^2 那双曲线的公式呢 跟椭圆的这个一样吗
e=c/a
=√(a²+b²)/a
=√[1+(b/a)²]

二 : 我们把离心率为的双曲线称为黄金双曲线.如图(图2)给出
我们把离心率为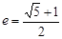 的双曲线 的双曲线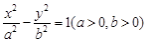 称为黄金双曲线.如图(图2)给出以下几个说法: 称为黄金双曲线.如图(图2)给出以下几个说法: ①双曲线  是黄金双曲线; ②若 是黄金双曲线; ②若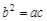 ,则该双曲线是黄金双曲线; ,则该双曲线是黄金双曲线;③若  ,则该双曲线是黄金双曲线;④若 ,则该双曲线是黄金双曲线;④若 ,则该双曲线是黄金双曲线.其中正确的是 ,则该双曲线是黄金双曲线.其中正确的是
|
| D |
双曲线 , , ①正确;若 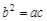 ,则 ,则 即 即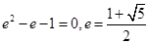 .②正确;若 .②正确;若 ,则 ,则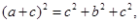 即 即 , ,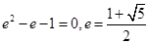 .③正确;若 .③正确;若 ,则 ,则 整理得 整理得 , , .④正确 .④正确 |
考点:
考点名称:双曲线的定义双曲线第一定义:
平面内与两定点F1,F2的距离的差的绝对值等于定长2a(小于|F1F2|)的点的轨迹叫双曲线,即||PF1|-|PF2||=2a(2a<|F1F2|)。若2a=|F1F2|,则轨迹是以F1,F2为端点射线,若2a>|F1F2|,则轨迹不存在;若去掉定义中的绝对值则轨迹仅表示双曲线的一支。
双曲线的第二定义:
平面内与一个定点F和一条定直线l的距离的比是常数e(e>1)的动点的轨迹叫双曲线。
双曲线的理解:
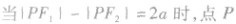 的轨迹为近
的轨迹为近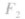 的一支;
的一支; 的一支。
的一支。
注: 的延长线和反向延长线(两条射线);
的延长线和反向延长线(两条射线); 则轨迹不存在;
则轨迹不存在; 的垂直平分线。
的垂直平分线。
三 : 一对共轭双曲线的离心率分别为e1和e2,则e1+e2的最小值
一对共轭双曲线的离心率分别为e1和e2,则e1+e2的最小值为( )
|
双曲线
∵e1=
∵c2=a2+b2,ab≤(
∵(
故选C. |
考点:
考点名称:双曲线的性质(顶点、范围、对称性、离心率)双曲线的离心率的定义:
(1)定义:双曲线的焦距与实轴长的比 叫做双曲线的离心率.
叫做双曲线的离心率.
(2)e的范围:e>l.
(3)e的含义:e是表示双曲线开口大小的一个量,e越大开口越大.
渐近线与实轴的夹角也增大。
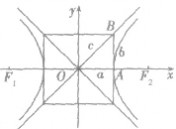
双曲线的性质:
1、焦点在x轴上:顶点:(a,0),(-a,0);焦点:(c,0),(-c,0);
渐近线方程: 或
或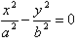 。
。
2、焦点在y轴上:顶点:(0,-a),(0,a);焦点:(0,c),(0,-c);
渐近线方程: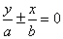 或
或 。
。
3、轴:x、y为对称轴,实轴长为2a,虚轴长为2b,焦距2c。
4、离心率 ;
;
5、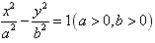 中,取值范围:x≤-a或x≥a,y∈R,对称轴是坐标轴,对称中心是原点。
中,取值范围:x≤-a或x≥a,y∈R,对称轴是坐标轴,对称中心是原点。
双曲线的焦半径:
双曲线上的点 之间的线段长度称作焦半径,分别记作
之间的线段长度称作焦半径,分别记作



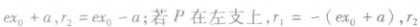



 关于双曲线的几个重要结论:(1)弦长公式(与椭圆弦长公式相同).
关于双曲线的几个重要结论:(1)弦长公式(与椭圆弦长公式相同). 的两个焦点,P为双曲线上一点(异于顶点),
的两个焦点,P为双曲线上一点(异于顶点), 的面积为
的面积为

 (4)双曲线的一个焦点到一条渐近线的距离等于虚半轴长.
(4)双曲线的一个焦点到一条渐近线的距离等于虚半轴长. 上一点P(x0,y0)处的切线方程是
上一点P(x0,y0)处的切线方程是
 ,我们有:P(x0,y0)在双曲线内部(与焦点共区域)
,我们有:P(x0,y0)在双曲线内部(与焦点共区域) P(x0,y0)在双曲线外部(与焦点不其区域) 本文标题:双曲线的离心率-双曲线的离心率公式
P(x0,y0)在双曲线外部(与焦点不其区域) 本文标题:双曲线的离心率-双曲线的离心率公式 61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1