一 : (2014自贡)23.阅读理解:如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC
(2014自贡)
23.(12分)阅读理解:
如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题:
(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.

二 : 如图,在四边形ABCD中,AD∥BC,点E是AB上的一个动点,
如图,在四边形ABCD中,AD∥BC,点E是AB上的一个动点,若∠B=60°,AB=BC,且∠DEC=60°,判断AD+AE与BC的关系并证明你的结论.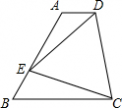 |
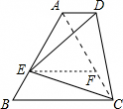 有BC=AD+AE. 连接AC,过E作EF∥BC交AC于F点. ∵∠B=60°,AB=BC,∴△ABC为等边三角形, ∵EF∥BC,∴△AEF为等边三角形. 即AE=EF,∠AEF=∠AFE=60°. 所以∠CFE=120°. (3分) 又AD∥BC,∠B=60°故∠BAD=120°. 又∠DEC=60°,∠AEF=60°. 所以∠AED=∠FEC. (1分) 在△ADE与△FCE中, ∠EAD=∠CFE,AE=EF,∠AED=∠FEC, 所以△ADE≌△FCE. 所以AD=FC. (1分) 则BC=AD+AE. (1分) |
考点:
考点名称:等边三角形等边三角形定义:性质:
①等边三角形是锐角三角形,等边三角形的内角都相等,且均为60°。
②等边三角形每条边上的中线、高线和所对角的平分线互相重合(三线合一)
③等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线 或对角的平分线所在的直线。
④等边三角形重心、内心、外心、垂心重合于一点,称为等边三角形的中心。(四心合一)
⑤等边三角形内任意一点到三边的距离之和为定值(等于其高)
判定方法:
①三边相等的三角形是等边三角形(定义)
②三个内角都相等(为60度)的三角形是等边三角形
③有一个角是60度的等腰三角形是等边三角形
④两个内角为60度的三角形是等边三角形
说明:可首先考虑判断三角形是等腰三角形。
等边三角形的性质与判定理解:
首先,明确等边三角形定义。三边相等的三角形叫做等边三角形,也称正三角形。
其次,明确等边三角形与等腰三角形的关系。等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形。
等比三角形的尺规做法:
可以利用尺规作图的方式画出正三角形,其作法相当简单:先用尺画出一条任意长度的线段(这条线段的长度决定等边三角形的边长),再分别以线段二端点为圆心、线段为半径画圆,二圆汇交于二点,任选一点,和原来线段的两个端点画线段,则这二条线段和原来线段即构成一正三角形。
三 : 如图,在四边形ABCD中,AD∥BC,点E是AB上的一个动
如图,在四边形ABCD中,AD∥BC,点E是AB上的一个动点,若∠B=60°,AB=BC,且∠DEC=60°,判断AD+AE与BC的关系并证明你的结论.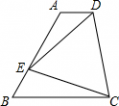 |
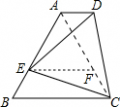 有BC=AD+AE. 连接AC,过E作EF∥BC交AC于F点. ∵∠B=60°,AB=BC,∴△ABC为等边三角形, ∵EF∥BC,∴△AEF为等边三角形. 即AE=EF,∠AEF=∠AFE=60°. 所以∠CFE=120°. (3分) 又AD∥BC,∠B=60°故∠BAD=120°. 又∠DEC=60°,∠AEF=60°. 所以∠AED=∠FEC. (1分) 在△ADE与△FCE中, ∠EAD=∠CFE,AE=EF,∠AED=∠FEC, 所以△ADE≌△FCE. 所以AD=FC. (1分) 则BC=AD+AE. (1分) |
考点:
考点名称:等边三角形等边三角形定义:性质:
①等边三角形是锐角三角形,等边三角形的内角都相等,且均为60°。
②等边三角形每条边上的中线、高线和所对角的平分线互相重合(三线合一)
③等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线 或对角的平分线所在的直线。
④等边三角形重心、内心、外心、垂心重合于一点,称为等边三角形的中心。(四心合一)
⑤等边三角形内任意一点到三边的距离之和为定值(等于其高)
判定方法:
①三边相等的三角形是等边三角形(定义)
②三个内角都相等(为60度)的三角形是等边三角形
③有一个角是60度的等腰三角形是等边三角形
④两个内角为60度的三角形是等边三角形
说明:可首先考虑判断三角形是等腰三角形。
等边三角形的性质与判定理解:
首先,明确等边三角形定义。三边相等的三角形叫做等边三角形,也称正三角形。
其次,明确等边三角形与等腰三角形的关系。等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形。
等比三角形的尺规做法:
可以利用尺规作图的方式画出正三角形,其作法相当简单:先用尺画出一条任意长度的线段(这条线段的长度决定等边三角形的边长),再分别以线段二端点为圆心、线段为半径画圆,二圆汇交于二点,任选一点,和原来线段的两个端点画线段,则这二条线段和原来线段即构成一正三角形。
四 : 如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠C
如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,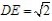 , , 。求CD的长和四边形ABCD的面积。 。求CD的长和四边形ABCD的面积。 |
 |
解:过D作DF AC于F如图, AC于F如图,∵ 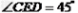 , ,∴ 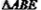 、 、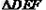 均为等腰直角三角形 均为等腰直角三角形∵DE= 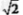 , ,∴EF=DF=1, ∴CD=2DF=2, CF=  , ,又∵BE=2 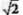 , ,∴AB=AE=2, S四ABCD=S△ABC+S△ACD =  AC(AB+DF) AC(AB+DF)= 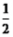 ×(3+ ×(3+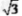 )×3 )×3= 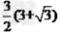 |  |
考点:
考点名称:等腰三角形的性质,等腰三角形的判定定义:等腰三角形的性质:
1.等腰三角形的两个底角度数相等(简写成“等边对等角”)。
2.等腰三角形的顶角的平分线,底边上的中线,底边上的高重合(简写成“等腰三角形的三线合一”)。
3.等腰三角形的两底角的平分线相等(两条腰上的中线相等,两条腰上的高相等)。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(需用等面积法证明)。
7.等腰三角形是轴对称图形,只有一条对称轴,顶角平分线所在的直线是它的对称轴,等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)
等腰三角形的判定:
1.定义法:在同一三角形中,有两条边相等的三角形是等腰三角形。
2.判定定理:在同一三角形中,有两个角相等的三角形是等腰三角形(简称:等角对等边)。
3.顶角的平分线,底边上的中分线,底边上的高的重合的三角形是等腰三角形。
 ;
;
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1