一 : 高一数学集合测试题

高一数学集合测试题 班级姓名

一、单选题：

1．设全集I={0，1，2，3，4}，集合A={0，1，2，3}，集合B={2，3，4}，则CIA∪CIB=

A．{0}

?2x?3y?1B．{0，1} C．{0，1，4} D．{0，1，2，3，4} x?y?3的解的集合是 2．方程组??

A．｛x =8,y=5｝ B．｛8, 5｝ C．｛(8, 5)｝ D．?

3．有下列四个命题： ①?0?是空集； ②若a?Z，则?a?N；

?6?③集合A?x?Rx2?2x?1?0有两个元素；④集合B??x?Q?N?是有限集。(www.61k.com] x??

其中正确命题的个数是

A．0 B．1 C．2 D．3 ??

4．如果集合A={x|ax2＋2x＋1=0}中只有一个元素，则a的值是

A．0 B．0 或1 C．1 D．不能确定

5．已知M?yy?x2?4,x?R?，P??x2?x?4?则M与P的关系是 ?

A．M=P B．M?P C．M∩P=? D． M ?P

6．已知全集I＝N，集合A＝{x|x＝2n，n∈N}，B＝{x|x＝4n，n∈N}，则

A．I＝A∪B B．I＝CIA∪B C．I＝A∪CIB D．I＝CIA∪CIB

7．设集合M={x|x?

A．M =N k1k1?,k?Z},N?{x|x??,k?Z}，则 2442B． M?N ?C． N?M ?D．M∩N??

8．设集合A={x|1＜x＜2}，B={x|x＜a}满足A??B，则实数a的取值范围是

A．?2,??? B．???,1? C．?1,??? D．???,2?

?9．满足{1，2，3} ??M ?{1，2，3，4，5，6}的集合M的个数是

A．8 B．7 C．6 D．5

10．如右图所示，I为全集，M、P、S为I的子集。

则阴影部分所表示的集合为

A．(M∩P)∪S B．(M∩P)∩S

C．(M∩P)∩(I S)

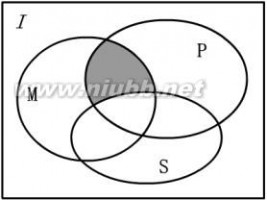
D．(M∩P)∪(I S)

第 1 页 共 5 页

高一数学集合练习题 高一数学集合测试题

11．已知A??y|y?x2?1,x?R,y?R?，全集U?R，则?e UA??N? 12．已知M??a,b?，N??b,c,d?，若集合P满足P

M且P N，则P可是 ．

13．设全集U＝{a，b，c，d，e}，A＝{a，c，d}，B＝{b，d，e}，

则?UA∩?UB＝________.

14．已知?x|x2?2013?(a?2)x?a2?4?0???0?，则a?． 三、解答题：(写出必要的计算步骤，只写最后结果不得分)

15．已知集合A＝｛x｜－1＜x＜3}，A∩B＝?，A∪B＝R，求集合B．

16．已知集合A={x|1≤x＜4}，B={x|x＜a};若AB，求实数a的取值集合．

第 2 页 共 5 页

高一数学集合练习题 高一数学集合测试题

17．已知集合A={－3，4}，B={x|x2－2px＋q=0}，B≠?，且B?A，求实数p，q的值．

第 3 页 共 5 页

高一数学集合练习题 高一数学集合测试题

18．设A＝{x|－2≤x≤5}，B＝{x|m－1≤x≤2m＋1}，

(1)当x∈N*时，求A的子集的个数；

(2)当x∈R且A∩B＝?时，求m的取值范围．

第 4 页 共 5 页

高一数学集合练习题 高一数学集合测试题

高一数学集合周末练习20130907参考答案

一、选择题：CCABD CBACC

二、填空题： 11、?0?． 12、?、?b? 13、解：?UA∩?UB＝?U(A∪B)，而A∪B＝{a，b，c，d，e}＝U. 答案：? ． 14、?2．

三、解答题：

15.解：由A∩B＝?及A∪B＝R知全集为R，CR A＝B，

故B＝CR A＝｛x｜x≤－1或x≥3｝．

16.解： 将数集A表示在数轴上(如图)，要满足A B，表示数a的点必须在4或4的右边，所求a的取值集合为{a|a≥4}.

?9?6p?q?0?p??3?17.解：⑴若B=??3?则B?A,?? ?2???4p?4q?0?q?9

?16?8p?q?0?p?4??⑵若B?{4},则B?A,?? ， 2q?16??4p?4q?0??

⑶若B={－3，4}则B?A 1??9?6p?q?0?p?则???2.16?8p?q?0???q??12

*1??p??3?p?4?p??综上?或?或?2 q?9q?16????q??1218．解：(1)∵x∈N且A＝{x|－2≤x≤5}，

∴A＝{1,2,3,4,5}．故A的子集个数为25＝32个．

(2)∵A∩B＝?，

∴m－1>2m＋1或2m＋1<－2或m－1>5，

∴m<?或m>6.

32第 5 页 共 5 页

二 : 人教版高中数学必修一期末测试题[1]

期末测试题

考试时间：90分钟 试卷满分：100分

一、选择题：本大题共14小题，每小题4分，共56分．在每小题的4个选项中，只有一项是符合题目要求的．

1．设全集U＝R，A＝{x|x＞0}，B＝{x|x＞1}，则A∩UB＝( )．

A．{x|0≤x＜1} B．{x|0＜x≤1} C．{x|x＜0} D．{x|x＞1}

2．下列四个图形中，不是以x为自变量的函数的图象是( )． ．．

A B C D

3．已知函数 f(x)＝x2＋1，那么f(a＋1)的值为( )．

A．a2＋a＋2 B．a2＋1 C．a2＋2a＋2 D．a2＋2a＋1

4．下列等式成立的是( )．

A．log2(8－4)＝log2 8－log2 4

C．log2 23＝3log2 2 B．log88＝log2 log244D．log2(8＋4)＝log2 8＋log2 4

5．下列四组函数中，表示同一函数的是( )．

A．f(x)＝|x|，g(x)＝x2

B．f(x)＝lg x2，g(x)＝2lg x

x2－1C．f(x)＝，g(x)＝x＋1 x－1

1·x－1，g(x)＝x2－D．f(x)＝x＋1

6．幂函数y＝xα(α是常数)的图象( ).

A．一定经过点(0，0)

C．一定经过点(－1，1) B．一定经过点(1，1) D．一定经过点(1，－1)

7．国内快递重量在1 000克以内的包裹邮资标准如下表：

第 1 页 共 6 页

人教版高一数学必修一 人教版高中数学必修一期末测试题[1]

如果某人从北京快递900克的包裹到距北京1 300 km的某地，他应付的邮资是( ). A．5.00元

B．6.00元

C．7.00元

D．8.00元

8．方程2x＝2－x的根所在区间是( ). A．(－1，0)

b

B．(2，3) C．(1，2) D．(0，1)

?1?

9．若log2 a＜0，??＞1，则( ).

?2?

A．a＞1，b＞0

B．a＞1，b＜0 D．0＜a＜1，b＜0

C．0＜a＜1，b＞0

10．函数y＝－4x的值域是( ). A．[0，＋∞)

B．[0，4]

C．[0，4)

D．(0，4)

11．下列函数f(x)中，满足“对任意x1，x2∈(0，＋∞)，当x1＜x2时，都有f(x1)＞f(x2)的是( ).

A．f(x)＝

1 x

B．f(x)＝(x－1)2 D．f(x)＝ln(x＋1)

C ．f(x)＝ex

12．奇函数f(x)在(－∞，0)上单调递增，若f(－1)＝0，则不等式f(x)＜0的解集是( ).

A．(－∞，－1)∪(0，1) C．(－1，0)∪(0，1)

B．(－∞，－1)∪(1，＋∞) D．(－1，0)∪(1，＋∞)

?logx，x＞0

13．已知函数f(x)＝?2，则f(－10)的值是( ).

f(x＋3)，x≤ 0?

A．－2 B．－1 C．0 D．1

14．已知x0是函数f(x)＝2x＋有( ).

A．f(x1)＜0，f(x2)＜0 C．f(x1)＞0，f(x2)＜0

1

的一个零点．若x1∈(1，x0)，x2∈(x0，＋∞)，则1－x

B．f(x1)＜0，f(x2)＞0 D．f(x1)＞0，f(x2)＞0

二、填空题：本大题共4小题，每小题4分，共16分．将答案填在题中横线上．

第 2 页 共 6 页

人教版高一数学必修一 人教版高中数学必修一期末测试题[1]

15．A＝{x|－2≤x≤5}，B＝{x|x＞a}，若A?B，则a取值范围是．

16．若f(x)＝(a－2)x2＋(a－1)x＋3是偶函数，则函数f(x)的增区间是 ．

17．函数y＝log2x－2的定义域是

?1?18．求满足???4?x2－8＞4－2x的x的取值集合是

三、解答题：本大题共3小题，共28分．解答应写出文字说明、证明过程或演算步骤．

19．(8分) 已知函数f(x)＝lg(3＋x)＋lg(3－x)．

(1)求函数f(x)的定义域；

(2)判断函数f(x)的奇偶性，并说明理由．

第 3 页 共 6 页

人教版高一数学必修一 人教版高中数学必修一期末测试题[1]

20．(10分)已知函数f(x)＝2|x＋1|＋ax(x∈R)．

(1)证明：当 a＞2时，f(x)在 R上是增函数．

(2)若函数f(x)存在两个零点，求a的取值范围．

21．(10分)某租赁公司拥有汽车100辆．当每辆车的月租金为3 000元时，可全部租出．当每辆车的月租金每增加50元时，未租出的车将会增加一辆．租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．

(1)当每辆车的月租金定为3 600元时，能租出多少辆车？

(2)当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？

第 4 页 共 6 页

人教版高一数学必修一 人教版高中数学必修一期末测试题[1]

参考答案

一、选择题

1．B

解析：UB＝{x|x≤1}，因此A∩UB＝{x|0＜x≤1}．

2．C

3．C

4．C

5．A

6．B

7．C

8．D

9．D

?1?解析：由log2 a＜0，得0＜a＜1，由??＞1，得b＜0，所以选D项． ?2?b

10．C

解析：∵ 4x＞0，∴0≤16－ 4x＜16，∴－4x∈[0，4)．

11．A

解析：依题意可得函数应在(0，＋∞)上单调递减，故由选项可得A正确．

12．A

13．D

14．B

解析：当x＝x1从1的右侧足够接近1时，

f(x1)＜0；当x＝x2足够大时，

选项是B．

二、填空题

15．参考答案：(－∞，－2)．

16．参考答案：(－∞，0)．

17．参考答案：[4，＋∞)．

第 5 页 共 6 页 1是一个绝对值很大的负数，从而保证 1－x1可以是一个接近0的负数，从而保证f(x2)＞0．故正确1－x

人教版高一数学必修一 人教版高中数学必修一期末测试题[1]

18．参考答案：(－8，＋∞)．

三、解答题

?3＋x＞019．参考答案：(1)由?，得－3＜x＜3， 3－x＞0?

∴ 函数f(x)的定义域为(－3，3)．

(2)函数f(x)是偶函数，理由如下：

由(1)知，函数f(x)的定义域关于原点对称，

且f(－x)＝lg(3－x)＋lg(3＋x)＝f(x)，

∴ 函数f(x)为偶函数．

(a＋2)x＋2，x≥ －1?20．参考答案：(1)证明：化简f(x)＝? (a－2)x－2，x＜－1?

因为a＞2，

所以，y1＝(a＋2)x＋2 (x≥－1)是增函数，且y1≥f(－1)＝－a；

另外，y2＝(a－2)x－2 (x＜－1)也是增函数，且y2＜f(－1)＝－a．

所以，当a＞2时，函数f(x)在R上是增函数．

(2)若函数f(x)存在两个零点，则函数f(x)在R上不单调，且点(－1，－a)在x轴下方，

(a＋2)(a－2)＜0?所以a的取值应满足? 解得a的取值范围是(0，2)． －a＜0?

21．参考答案：(1)当每辆车的月租金定为3 600元时，未租出的车辆数为

＝12，所以这时租出了100－12＝88辆车．

(2)设每辆车的月租金定为x元，则租赁公司的月收益为 3 600－3 00050

1x－3 000?x－3 000?f(x)＝?100－×50＝－(x－4 050)2＋307 050． ?(x－150)－50?5050?

所以，当x＝4 050 时，f(x)最大，其最大值为f(4 050)＝307 050．

当每辆车的月租金定为4 050元时，月收益最大，其值为307 050元．

第 6 页 共 6 页

三 : 高中数学必修2同步测试卷全套

高中数学必修2同步测试卷全套

［新课标人教A版］

目 录 ................................................................................................................................. 错误！未定义书签。

第一章 空间几何体 ................................................................................................................................................. 2

1.1 空间几何体的结构 .................................................................................................................................... 2

1.3 柱体、锥体、台体的表面积 .................................................................................................................... 7

1.3 柱体、锥体与台体的体积 ................................................................................................................. 10

1.4 球的体积和表面积 .................................................................................................................................. 14

第一章 空间几何体 单元测试1 .................................................................................................................. 18

第二章 空间几何体 单元测试2 .................................................................................................................. 21

第一章 空间几何体 检测题3 ...................................................................................................................... 24

第一章 空间几何体 单元测试4 .................................................................................................................. 28

第二章 空间点、直线、平面间的位置关系 ....................................................................................................... 31

2.1空间点、直线、平面间的位置关系 ....................................................................................................... 31

2.2 直线、平面平行的判定及其性质 .......................................................................................................... 39

2.3 直线平面垂直的判定及其性质 .............................................................................................................. 56

第二章点、直线、平面之间的位置 单元测试1 ......................................................................................... 66

第二章 点、直线、平面之间的位置关系 单元测试2 ............................................................................... 68

第二章 点、直线、平面之间的位置关系单元测试3 ................................................................................. 71

第三章 直线与方程 ............................................................................................................................................... 75

3.1.1 直线的倾斜角和斜率 ........................................................................................................................... 75

3.1.2 两条直线平行与垂直的判定 ............................................................................................................... 77

3.1.3 直线的倾斜角和斜率 ........................................................................................................................... 81

3.2.1 直线的方程 ........................................................................................................................................... 84

3.2.2 直线的方程 ........................................................................................................................................... 86

3.2.3 直线的方程 ........................................................................................................................................... 88

3.2.4 直线的方程 ........................................................................................................................................... 90

新课标高一数学同步测试—3.2直线方程 （1） ........................................................................................ 92

3.2 直线的方程 单元测试（2） .................................................................................................................. 98

3.2直线的方程 同步测试（3） ................................................................................................................. 103

3.3 直线的交点坐标与距离公式 同步测试................................................................................................ 111

3.3直线的交点坐标与距离公式 ..................................................................................................................114

第三章 直线与方程 单元测试1 .............................................................................................................. 124

第三章 直线与方程 单元测试2 .............................................................................................................. 129

第三章 直线与方程 单元测试3 ................................................................................................................ 133

第四章 圆的方程 ................................................................................................................................................. 137

4.2 圆的方程 同步测试 .............................................................................................................................. 140

4.2 直线、圆的位置关系测试 .................................................................................................................... 146

4.3空间直角坐标系 ..................................................................................................................................... 152 直线和圆 ....................................................................................................................................................... 158 必修3同步测试卷全套.. 必修4同步测试卷全套.. 必修5同步测试卷全套..

第一章 空间几何体第一章 空间几何体1.1 空间几何体的结构

第1页 共159页

第一章 空间几何体

1.1 空间几何体的结构

一、选择题

1．在棱柱中（ ）

A．只有两个面平行

B．所有的棱都平行

C．所有的面都是平行四边形

D．两底面平行，且各侧棱也互相平行

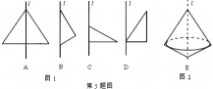
2．将图1所示的三角形线直线l旋转一周，可以得到如图2所示的几何体的是哪一个三角形（ ）

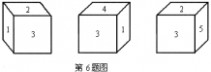
3．如图一个封闭的立方体，它6个表面各标出1、2、3、4、5、6这6个数字，现放成下面3个不同

的位置，则数字l、2、3对面的数字是（ ）

A．4、5、6 B．6、4、5 C．5、4、6 D．5、6、4

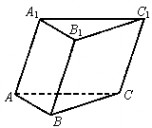
4．如图，能推断这个几何体可能是三棱台的是（ ）

A．A1B1＝2，AB＝3，B1C1＝3，BC＝4

B．A1Bl＝1，AB＝2，BlCl＝1.5，BC＝3，A1C1＝2，AC＝3

C．AlBl＝1，AB＝2，B1Cl＝1.5，BC＝3，AlCl＝2，AC＝4

D．AB＝A1B1，BC＝B1C1，CA＝C1A1

5．有下列命题

（1）在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；

（2）圆锥顶点与底面圆周上任意一点的连线是圆锥的母线；

（3）在圆台上、下底面圆周上各取一点，则这两点的连线是圆台的母线；

（4）圆柱的任意两条母线所在的直线是互相平行的．

其中正确的是（ ）

第一章 空间几何体第一章 空间几何体1.1 空间几何体的结构

第2页 共159页

A．（1）（2） B．（2）（3） C．（1）（3） D．（2）（4）

6．下列命题中错误的是（ ）

A．圆柱的轴截面是过母线的截面中面积最大的一个

B．圆锥的轴截面是所有过顶点的截面中面积最大的一个

C．圆台的所有平行于底面的截面都是圆

D．圆锥所有的轴截面是全等的等腰三角形

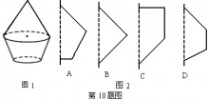
7．图1是由图2中的哪个平面图旋转而得到的（ ）

二、填空题

8如图，长方体ABCD—A1BlClD1中，AD＝3，AAl＝4，AB＝5，则从A点沿表面到Cl的最短距离为______．

9在三棱锥S—ABC中，SA＝SB＝SC＝1，∠ASB＝∠ASC＝∠BSC＝30°，如图，一只蚂蚁从点A出

发沿三棱锥的表面爬行一周后又回到A点，则蚂蚁爬过的最短路程为_____．

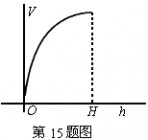
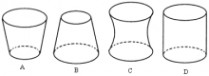
10高为H的水瓶中注水，注满为止，如果注水量V与水深h的函数关系的图象如图所示，那么水瓶的形状是______．

第一章

空间几何体第一章 空间几何体1.1 空间几何体的结构

第3页 共159页

11图，这是一个正方体的表面展开图，若把它再折回成正方体后，有下列命题：

①点H与点C重合；

②点D与点M与点R重合；

③点B与点Q重合；

④点A与点S重合．

其中正确命题的序号是____．（注：把你认为正确的命题的序号都填上）

三、解答题

12请给以下各图分类．

13别画一个三棱锥和一个四棱台．

14面体至少有几个面?这个多面体是怎样的几何体?

15合下图，说说它们分别是怎样的多面体?

第一章 空间几何体第一章 空间几何体1.1 空间几何体的结构

第4页 共159页

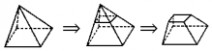
16察以下几何体的变化，通过比较，说出他们的特征．

17一个圆锥截成圆台，已知圆台的上下底面半径的比是1∶4，母线长为10cm，求圆锥的母线长____．

第一章 空间几何体第一章 空间几何体1.1 空间几何体的结构

第5页 共159页

参考答案

巩固练习

一、选择题

1．D 2． B 3C 4C 5D 6。B 7、A

二、填空题

8．74 9、2 10．B 11．②④

三、解答题

12．解：（1）（8）为球体，（2）为圆柱体，（3）为圆锥体

（4）为圆台体，（5）为棱锥体，（6）为棱柱体，（7）为两棱锥的组合体．

13．解：画三棱锥可分三步完成

第一步：画底面——画一个三角形；

第二步：确定顶点——在底面外任一点；

第三步：画侧棱——连结顶点与底面三角形各顶点．

画四棱可分三步完成

第一步：画一个四棱锥；

第二步：在四棱锥一条侧棱上取一点，从这点开始，顺次在各个面内画与底面对应线段平行的线段； 第三步：将多余线段擦去．

14．解：多面体至少有4个面，它是三棱锥．

15．解：第一个图是二十面体，它有二十个面；

第二个图是十二面体，它有十二个面；

第三个图是八面体，它有八个面；

第四个图是六面体，它有六个面

第五个图是四面体，它有四个面．

16．略

40

17．3cm

第一章 空间几何体第一章 空间几何体1.1 空间几何体的结构

第6页 共159页

1.3 柱体、锥体、台体的表面积

一、选择题

1．正四棱柱的对角线长是9cm，全面积是144cm2，则满足这些条件的正四棱柱的个数是（ ）

A．0个 B．1个 C．2个 D．无数个

2．三棱柱ABC—A1B1C1中，AB＝AC，且侧面A1ABB1与侧面A1ACCl的面积相等，则∠BB1C1等于（ ）

A．45° B．60° C．90° D．120°

3．边长为5cm的正方形EFGH是圆柱的轴截面，则从正点沿圆柱的侧面到相对顶点G的最短距离是（ ）

A．10cm B．52cm

52?42 C．5?1cm D．2cm

3

4．中心角为4π，面积为B的扇形围成一个圆锥，若圆锥的全面积为A，则A∶B等于（ ）

A．11∶8 B．3∶8 C．8∶3 D．13∶8

5．正六棱台的上、下底面的边长分别为a、b（a<b），侧面和底面所成的二面角为60°，则它的侧面积是（ ）

A．3（b2－a2） B．2（b2－a2）

C．（b2－a2） D．2（b2－a2）

6．过圆锥的高的三等分点作平行于底面的截面，它们把圆锥的侧面分成的三部分的面积之比为（ ）

A．1∶2∶3 B．1∶3∶5

C．1∶2∶4 D．1∶3∶9

7．若圆台的上、下底面半径的比为3∶5，则它的中截面分圆台上、下两部分面积之比为（ ）

A．3∶5 B．9∶25

C．5∶41 D．7∶9

8．一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是（ ）

1?2?1?2?1?2?1?4?

A．2? B．4? C．? D．2?

9．已知正四面体ABCD的表面积为S，其四个面的中心分别为E、F、G、H，设四面体EFGH的表

T

面积为T，则S等于（ ）

1411

A．9 B．9 C．4 D．3

10．一个斜三棱柱，底面是边长为5的正三角形，侧棱长为4，侧棱与底面三角形两边所成的角都是60°，则这个斜三棱柱的侧面积是（ ）

A．40 B．20(1?3) C．30(1?) D．303

二、填空题

11．长方体的高为h，底面面积是M，过不相邻两侧棱的截面面积是N，则长方体的侧面积是______．

12．正四棱台上、下底面的边长为b、a（a＞b）且侧面积等于两底面面积之和，则棱台的高是______．

13．圆锥的高是10 cm，侧面展开图是半圆，此圆锥的侧面积是_____；轴截面等腰三角形的顶角为______．

14．圆台的母线长是3 cm，侧面展开后所得扇环的圆心角为180°，侧面积为10πcm2，则圆台的高为_____；上下底面半径为_______．

第一章 空间几何体第一章 空间几何体1.3 柱体、锥体、台体的表面积

第7页 共159页

三、解答题

15．已知正三棱台的侧面和下底面所成的二面角为60°，棱台下底面的边长为a，侧面积为S，求棱台上底面的边长．

16．圆锥的底面半径为5 cm，高为12 cm，当它的内接圆柱的底面半径为何值时，圆锥的内接圆柱全面积有最大值？最大值是多少?

17．圆锥底面半径为r，母线长是底面半径的3倍，在底面圆周上有一点A，求一个动点P自A出发在侧面上绕一周到A点的最短路程．

参考答案

一、选择题

1．C 设正四棱柱的底面边长为a，高为c，由题意

2a2＋c2＝81①

2a2＋4ac2＝144 即a2＋2ac2＝72②

①×8－②×9得7a2－18ac＋8c2＝0即（7a－4c）（a－2c）＝0，因此7a－4c＝0或a＝2c，由此可见由①②构成方程组有两组满足条件的解，故正确答案选C．

2．C 3．D 4．A 5．A 6．B 7．D

8．A设底面圆半径为r，母线即高为h．∴h＝2πr． 2?r2＋2?rhr＋hr＋2?r1＋2?

2?rh∴S侧＝＝h＝2?r＝2?．

∴应选A．

9．A

10．B 可计算出直截面的周长为5＋5，则S侧＝4（5＋53）＝20（1＋）．另解：如图，若∠A1AC＝∠A1AB＝60°，则可证明□BB1C1C为矩形，因此，S侧＝2S□AA1B1B＋

×5＝20（1＋）．

S全S矩形BB1C1C＝2×4×5×sin60°＋4

二、填空题

11．2N＋2Mh． 22

设长方体的长和宽分别为a，b则有a·b＝M，a＋b·h＝N， 22

N2

22＋2M222a＋b）h2（a＋b）h＝2·h＝·h＝2N＋2Mh．

11293ab200?12．a＋b 13．3；60° 14．2cm；2cm，2cm

三、解答题．

15．设O，O1分别为下，上底面中心，连接OO1，则OO1⊥平面ABC，上底面边长为x，连接AO，A1O1并延长交BC，B1C1分别于D、D1两点．

则AD⊥BC，连接DD1，则DD1⊥BC，∠ADD1为二面角A－BC－D1的平面角，即∠ADD1＝60°，过D1作D1E∥OO1交AD于E，则D1E⊥平面ABC．

第一章 空间几何体第一章 空间几何体1.3 柱体、锥体、台体的表面积

第8页 共159页

3ax在正△ABC，△A1B1C1中，AD＝2，A1D1＝2．

1

在Rt△D1ED中，ED＝OD－OE＝3（AD－A1D1）＝6（a－x）．

（x＋aa－x）2则D1D＝2ED＝3（a－x），由题意S＝3·．

233a2－S223即S＝2（a－x）．解得x＝．

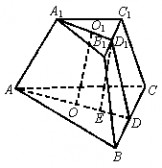
16．如图SAB是圆锥的轴截面，其中SO＝12，OB＝5．设圆锥内接圆柱底面半径为O1C＝x，由△SO1C∽

△SOB， SO1SOSO12xOC则1＝OB，SO1＝OB·O1C＝5，

1212xx55∴OO1＝SO－SO1＝12－，则圆柱的全面积S＝S侧＋2S底＝2π（12－）x＋2πx2＝2π（12x－

72x5）．

36030?2当x＝7cm时，S取到最大值7cm．

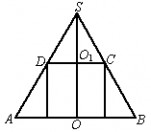
r

17．如图扇形SAA′为圆锥的侧面展开图，AA′即为所求的最知路程，由已知SA＝SA′＝3r，θ＝SA360°＝120°，在等腰△SAA′中可求得AA′＝3r．

第一章 空间几何体第一章 空间几何体1.3 柱体、锥体、台体的表面积

第9页 共159页

1.3 柱体、锥体与台体的体积

一、选择题

1．若正方体的全面积增为原来的2倍，那么它的体积增为原来的（ ）

A．2倍 B．4倍 C．2倍 D．22倍

2．一个长、宽、高分别为a、b、c长方体的体积是8cm2，它的全面积是32 cm2，且满足b2＝ac，那么这个长方体棱长的和是（ ）

A、28cm B．32 cm C．36 cm D．40 cm

3．正六棱台的两底面的边长分别为a和2a，高为a，则它的体积为（ ）

2133333733aaa373a222 A． B． C． D．

4．若球的体积与其表面积的数值相等，则球的半径为（ ）

1

A．1 B．3 C．2 D．2

5．一个球的外切正方体的全面积的数值等于6cm2，则此球的体积为（ ）

6641?cm3?cm3?cm3?cm3

A．3 B．8 C．6 D．6

33a 6．正六棱锥的底面边长为a，体积为2，那么侧棱与底面所成的角为（ ）

5????

A．6 B．4 C．3 D．12

7．正四棱锥的底面面积为Q，侧面积为S，则它的体积为（ ）

11QSQ(S2?Q2) A、3 B．2

11S(S2?Q2)Q(S2?Q2) C、2 D、6

8．棱台上、下底面面积之比为1∶9，则棱台的中截面分棱台成两部分的体积之比是（ ）

A．1∶7 B．2∶7 C．7∶19 D．3∶16

9．正方体、等边圆柱与球它们的体积相等，它们的表面积分别为S1、S2、S3，下面关系中成立的是（ ）

A．S3＞S2＞S1 B．S1＞S3＞S2

C．S1＞S2＞S3 D．S2＞Sl＞S3

10．沿棱长为1的正方体的交于一点的三条棱的中点作一个截面，截得一个三棱锥，那么截得的三棱锥的体积与剩下部分的体积之比是（ ）

A．1∶5 B．1∶23 C．1∶11 D．1∶47

二、填空题

11．底面边长和侧棱长都是a的正三棱锥的体积是_______．

第一章 空间几何体第一章 空间几何体1.3柱体、锥体与台体的体积

第10页 共159页

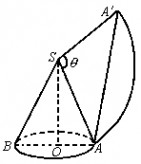
12．将4×6的矩形铁皮作为圆柱的侧面卷成一个圆柱，则圆柱的最大体积是_______．

13．半径为1的球的内接正方体的体积是________；外切正方体的体积是_______．

14．已知正三棱台上、下底面边长分别为2、4，且侧棱与底面所成角是45°，那么这个正三棱台的体积等于_______．

三、解答题

15．三棱锥的五条棱长都是5，另一条棱长是6，求它的体积．

16．两底面边长分别是15cm和10cm的正三棱台，它的侧面积等于两底面积的和，求它的体积．

17．一个圆锥形容器和一个圆柱形容器，它们的轴截面尺寸如图所示，两容器内所盛液体的体积正好相等，且液面高度h正好相同，求h．

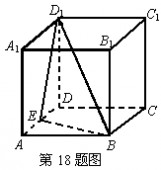
18．如图所示，已知正方体ABCD—A1B1ClDl的棱长为a，E为棱AD的中点，求点A1到平面BED1

的距离．

参考答案

一、选择题

1．D

b·c＝8?a·?16?ab＋bc＋ca＝

?22．B解：由已知?b＝ac①②③

③代入①得b3＝8，b＝2，ac＝4，代入②a＋c＝6．

∴长方体棱长的和为4（a＋b＋c）＝4×8＝32（cm2）．

3．D 4．B 5．C 6．B

7．D 设正四棱锥的底面边长和高分别为a，h，斜高为h′， 2a2a12h＋（）h＋4解得 2，S＝2（4a）h′＝2a则h′＝2

2S2Q1S2a－－24Q4＝24＝h＝4aS2－Q2Q．

111

V＝3h·Q＝3（2S2－Q2122（S－Q）Q）Q＝6．

8．C 9．B

10．D由E、F、G分别为BB1，B1C1，B1A1的中点，可证明平面EFG∥平面BC1A1，因此

第一章

空间几何体第一章 空间几何体1.3柱体、锥体与台体的体积

第11页 共159页

本文标题：高中数学必修一测试题-高一数学集合测试题
本文地址： http://www.61k.com/1145906.html