一 : 代数式经典练习题

知识点1代数式

1、用运算符号把数或表示数的字母连结而成的式子，叫做代数式。[www.61k.com]

单独的一个数或字母也是代数式。

2、代数式求值的一般步骤：

（1）代数式化简

（2）代入计算

（3）对于某些特殊的代数式，可采用“整体代入”进行计算。

知识点2、单项式的概念

式子3x,?a2,xy,?2.6t3,?m它们都是数或字母的积，象这样的式子叫做单项式， 单独的一个数或一个字母也是单项式。

注意：单项式是一种特殊的式子，它包含一种运算、三种类型。一种运算是指数与字母、字母与字母之间只能是乘法的一种运算，不能有加、减、除等运算符号；三种类型是指：一是数字与字母相乘组成的式子，如2ab;二是字母与字母组成的式子，如xy3;三是单独的一个数或字母，如2，?a,m。

知识点3、单项式的系数

单项式中的数字因数叫做这个单项式的系数。

注意：（1）单项式的系数可以是整数，也可能是分数或小数。如2x4的系数是2；数是1ab3的系

3

（2）单项式的系数有正有负，确定一个单项式的系数，要注意包含在它前面的符号， ，2.7m的系数是2.7。 如－?2xy?的系数是－2

（3）对于只含有字母因素的单项式，其系数是1或－1，不能认为是0，如－xy的系数是－1；xy的系数是1。

（4）表示圆周率的?，在数学中是一个固定的常数，当它出现在单项式中时，应将其作为系数的一部分，而不能当成字母。如2?xy的系数就是2?

知识点4、单项式的次数

一个单项式中，所有字母的指数和叫做这个单项式的次数。

注意：（1）计算单项式的次数时，应注意是所有字母的指数和，不要漏掉字母指数是1的情况。如单项式2xyz的次数是字母x,y,z的指数和，即4＋3＋1=8，而不是7次，应注意字母Z的指数是1而不是0.

（2）单项式是一个单独字母时，它的指数是1，如单项式m的指数是1，单项式是单独的一个常数时，一般不讨论它的次数。

（3）单项式的指数只和字母的指数有关，与系数的指数无关。如单项式－2xyz的次数是2＋3＋4=9而不是13次。

（4）单项式通常根据实验室的次数进行命名。如6x是一次单项式，2xyz是三次单项式。 知识点5、多项式的有关概念

（1）多项式：几个单项式的和叫做多项式。

（2）多项式的项：多项式中的每个单项式叫做多项式的项。

（3）常数项：不含字母的项叫做常数项。

（4）多项式的次数：多项式里次数最高项的次数叫做多项式的次数。

（5）整式：单项式与多项式统称整式。 42344322

代数式练习题 代数式经典练习题

注意：a、概念中“几个单项式的和”是指两个或两个以上的单项式相加。（www.61k.com）如2a?3a?4x,2＋3－7等这样的式子都是多项式。

b、多项式的每一项都包含前面的符号，如多项式－2xy3?6a?9共有三项，它们分别是－

332xy,6a,－9,一个多项式中含有几个单项式就说这个多项式是几项式如－2xy?6a?9共有三项，所以就叫三项式。

c、多项式的次数不是所有项的次数之和，也不是各项字母的指数和，而是组成这个多项式的单项式中次数最高的那个单项式的次数，如多项式－2xy3?6a?9是由三个单项式－

332xy,6a,－9组成，而在这三个单项式中－2xy的次数最高，且为4次，所以这个多项式的次数就是4.这是一个四次三项式。对于一个多项式而言是没有系数这一说法的。 知识点6、整式的书写

（1）书写含乘法运算的式子

a、省乘号要小心。当式子中出现乘法运算时，有些乘号可以省略不写。字母与字母相乘、数字与字母相乘、数字（字母）与带括号的式子相乘、带括号的式子之间相乘时，其乘号可以不写或写作“?”，但对于数字与数字相乘时乘号则不能省略，也不能用“?”。

b、数字在前，字母在后。数字与字母相乘，数字与带括号的式子相乘时除中间乘号可以省略不写之外，还必须把数字写在字母或括号的前面。

c、带分数一定要化成假分数。

（2）书写含除法运算的式子

当式子中出现含有字母的除法运算时，结果一般不用“÷”，而改成分数线，如ab?4应写a?3ab作，?a?3??7应写作 47（3）书写含单位名称的式子 a、遇和差，括号加 b、是积商，直接放

知识点7、同类项的概念

像25m与－40m,4ab2与2ab这样，所含字母相同，并且相同字母的指数也相同的2

3项，叫做同类项。

注意：a、同类项必须具备两个条件：所含字母相同；相同字母的指数也分别相同。二者缺一不可。

b、同类项与系数、字母的排列顺序无关。

c、所有的常数项都是同类项，单独的一项不能说是同类项，同类项至少针对两项而言。 知识点8、合并同类项

（1）定义：把多项式中的同类项合并成一项，叫做合并同类项。

（2）法则：合并同类项后，所得系数是合并前各同类项系数的和，且字母部分不变。它可以用“一变”、“两不变”来概括。“一变”是指同类项的系数变；“两不变”是指相同字母和相同字母的指数不变。

口诀：同类项，需判断，两相同，是条件。

合并时，需计算，系数加，两不变。

注意：a、系数相加时，一定要带上各项前面的符号。

b、合并同类项一定要完全、彻底，不能有漏项。

c、只有是同类项才能合并。

d、合并同类项的结果可能是单项式也可能是多项式。

知识点9、去括号

法则：括号前面是正号，去掉括号不变号；括号前面是负号，去掉括号要变号。

代数式练习题 代数式经典练习题

代数式经典练习题

1. 在式子m+5,ab,a=1,0,π,3(x+y),

n?k

2

180

,x>3中，是代数式的有( )

A 6个 B 5个 C 4个 D 3个 2. 下列式子中不是整式的是（ ）

A －23x B

xy

2

1x

C 12x＋5x D 0

x?y3

1?xx

3．下列判断：（1）?

?

不是单项式；（2）是多项式；（3）0不是单项式；（4）

是整式，其中正确的有（ ）

A 1个 B 2个 C 3个 D 4个 4. 在下列代数式：

ab3,?4,?

23

abc,0,x?y,

3x

中，单项式有( )

A 3个 B 4个 C 5个 D 6个 5. 单项式?

2xy7

3

4

的次数是( )

A 8次 B 3次 C 4次 D 5次 6. 下列说法中正确的是( )

A 代数式一定是单项式 B 单项式一定是代数式 C 单项式x的次数是0 D单项式－π2x2y2的次数是6 7. 在下列代数式：

12

?2

A 2个 B 3个 C 4个 D 5个 8.下列说法正确的是( )

2

ab,

1

a?b,ab

2

?b?1,??3,

2

?

1

,x?x?1中，多项式有

2

A．单项式?C．

1x

x

2

3

的系数是?3 B．单项式?

2πab

2

324

的指数是7

是单项式 D．单项式可能不含有字母

9. 下列多项式次数为3的是( )

A －5x2＋6x－1 B πx2＋x－1 C a2b＋ab＋b2 D x2y2－2xy－1 10. 下列说法正确的是（ ）

A 3x－5的项是3x和5 B C

x?yz

x?12

xy3

和都是单项式

ab7

和x?2xy?y都是多项式 D

22

2x?12

和都是整式

11. 若m、n都是自然数，多项式am?b2n?2m?2n的次数是( )

A m B 2n C m?2n D m、2n中较大的数 12. 多项式8x2+mxy-5y2+xy-8中不含xy项，则m的值为（ ）

A 0 B 1 C -1 D -5

13. 当x＝1时，代数式px3＋qx＋1的值为2003，则当x＝－1时，代数式px3＋qx＋1的值

代数式练习题 代数式经典练习题

A －2001 B －2002 C －2003 D 2001

14.甲数为a ，甲数是乙数的8倍小3，用甲数表示乙数 ，

乙数是甲数的8倍小3，用甲数表示乙数 。（www.61k.com）

15.若?abm?1

是四次单项式，则m的值是 ，系数是 。

6

16. 单项式?a2b3的系数是，次数是。

17. 单项式?abc

324的系数是 ，次数是 ，多项式3x2y?8x2y2?9的最高次项为 。

18. 若单项式?n?2?x2y?n是关于x，y的三次单项式，则n?

19. 当2y－x＝5时，5(x?2y)2?3(?x?2y)?100的值是＿＿＿＿＿＿

20. 已知a?b

a?b?3，代数式2(a?b)

a?b?4(a?b)

3(a?b)的值为 。

21. 当x?1，时 ax5?bx3?cx?1?3，当x??1，时 ax5?bx3?cx?1?。

22. 写出系数是－2，且含有字母a、b的所有4次单项式：＿＿＿＿＿

23. 已知关于x的多项式(a－1)x5＋x|b＋2|－2x＋b是二次三项式，则a＝____，b＝____。

24. 受洪水影响，我国南方某市有x人急需转移到安全地带，原计划转移时间是a小时，由

于天气原因，必须提前2小时转移完毕，那么每小时需多转移______人.

4xy225. 已知多项式-6xy-7x3m-1y2+-xy-5是七次多项式，求m值. 33

26．已知式子9?6y?4y2?7，求2y2?3y?7的值

27. 当x?2时，代数式ax3?bx?1的值等于?17，那么当x??1时，求代数式12ax?3bx3?5

的值。

28. 已知代数式ax4?bx3?cx2?dx?3，当x?2时它的值为20；当x??2时它的值为16，

求x?2时，代数式ax4?cx2?3的值

29. 已知

30. 若多项式5x2y

31. 已知单项式?1

2

2xyx?y?3，求代数式3x?5xy?3y?x?3xy?y的值。 ??n?3?y?22是关于x，y的四次二项式，求m2?2mn?n2的值 xy43的次数与多项式a2?8am?1b?a2b2的次数相同，求m的值。 232. 当多项式?5x??2m?1?x??2?3n?x?1不含二次项和一次项时，求m、n的值。

33. 有一串单项式：－x，2x，－3x，4x，?，－19x，20x.①你能说出它们的规律是什

么吗？ ② 写出第2007个单项式； ③写出第n个，第(n＋1)个单项式。 2341920

二 : 代数式典型练习题

百度搜索：61阅读，发现并分享更多精彩生活。

第三讲：代数式同步练习及单元检测

课标要求

1.掌握用字母表示数，建立符号意识.

2.会列代数式表示简单的数量关系，会正确书写代数式，会求代数式的值.

3.在数学活动中，体会抽象概括的数学思想方法和“特殊?一般”相互转化的辨证关系.

典型例题

例1 某市出租车收费标准为：起步价5元，3千米后每千米价1.2元，则乘坐出租车走x(x﹥3)千米应付_______元.

例2 下列代数式中，书写正确的是（ ）

A. ab·2 B. a÷4 C. -4×a×b D. 3

例3 下列各题中，错误的是（ ）

A、代数式x2?y2的意义是x,y的平方和. B、代数式5(x+y)的意义是5与(x+y)的积

C、x 的5倍与y的和的一半，用代数式表示为5x?y

212xy E. 53mn F. -3×6 D、比x的2倍多3的数，用代数式表示为2x+3

友情提示：数学语言有文字语言、符号语言、图形语言.进行数学思维时，同学们要学会恰当使用各种语言推理分析，各种语言的互译是一种数学基本功.

例4 当x=1时，代数式px3?qx?1的值为2005，求x=－1时，代数式px3?qx?1 的值.

分析：当x=1时，px3?qx?1=p?q?1?2005，p+q=2004,

当x=－1时，px3?qx?1=－p?q?1?－（p+q）+1=－2004+1=－2003.

解：

提示：“整体”思想在数学解题中经常用到，请同学们在解题时恰当使用.

例5 下图是一个数值转换机的示意图，请你用x、y表示输出结果，并求输入x

的值为3，y的值为-2时的输出结果.

解：

提示：把图形语言翻译为符号语言的关键是识图，弄清图中运算顺序.

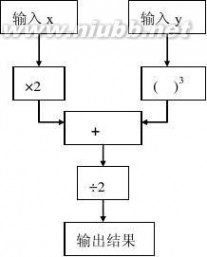
第 1 页 共 5 页

代数式 代数式典型练习题

例6

例7：观察：2=1×2，2+4=2×3，2+4+6=3×4，?，试推算2+4+6+?+2n的公式，并利用推算公式计算100+102+?+200．

强化练习

一、填空题

1. 代数式2a-b表示的意义是_____________________________.

2. 列代数式：⑴设某数为x,则比某数大20%的数为__________.⑵a、b两数的和的平方与它们差的平方和__________.

3. 有一棵树苗，刚栽下去时，树高2.1米，以后每年长0.3米，则n年后的树高为_____，计算10年后的树高为___米.

4. 某音像社对外出租光盘的收费方法是：每张光盘在出租后的头两天每天收0.8元，以后每天收0.5元，那么一张光盘在出租后第n天（n＞2的自然数）应收租金_________________________元.

5. 观察下列各式：12+1=1×2，22+2=2×3，32+3=3×4------请你将猜想到的规律用自然数n(n≥1)表示出来______________________.

6. 一个两位数，个位上的数是a，十位上的数字比个位上的数小3，这个两位数为______，当a=5时，这个两位数为______.

二、选择题

1. 某品牌的彩电降价30%以后，每台售价为a元，则该品牌彩电每台原价为（ ）

A. 0.7a元 B.0.3a元 C.10

3a 元 D. 10

7a元

2. 根据下列条件列出的代数式，错误的是（ ）

A. a、b两数的平方差为a2-b2 B. a与b两数差的平方为(a-b)2

C. a与b的平方的差为a2-b2 D. a与b的差的平方为(a-b)2

3. 如果a?2?(b?1)?0,那么代数式(a+b)2005的值为（ ） 2

A. –2005 B. 2005 C. -1 D. 1

4. 笔记本每本m元，圆珠笔每支n元，买x本笔记本和y支圆珠笔，共需（ ）

A. （ mx+ny）元 B. (m+n)(x+y) C. （nx+my ）元 D. mn(x+y) 元

5. 当x=-2,y=3时,代数式4x-2y的值为（ ） A. 14 B. –50 C. –14 D. 50

三、解答题

第 2 页 共 5 页 32

代数式 代数式典型练习题

1. 已知代数式3a-2a+6的值为8, 求23

2a?a?1的值. 2. 当a=-1,b=-212,c=11

2时，求代数式b-4ac的值，2

并指出求得的这个值是哪些数的平方.

3. 人在运动时的心跳速率通常和人的年龄有关.如果用a表示一个人的年龄，用b表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数，那么b=0.8(220-a).

⑴ 正常情况下,在运动时一个14岁的少年 ⑵ 一个45岁的人运动时10秒心跳的

所能承受的每分钟心跳的最高次数是多少？ 次数为22次，请问他有危险吗？为什么？

单元检测

一、填空题（每小题5分，共25分）

1. 某机关原有工作人员m人，现精简机构，减少20%的工作人员，则剩下_____人.

2. 结合生活经验作出具体解释：a-b__________________________________.

3. 甲以a千米/小时、乙以b千米/小时（a＞b）的速度沿同一方向前进，甲在乙的后面8千米处开始追乙，则甲追上

乙需_____________小时.

4. 若梯形的上底为a，下底为b，高为h，则梯形的面积为____________;当a=2cm，b=4cm，h=3cm时，梯形的面积

为____________.

5. 按下列程序计算x=3时的结果__________.

二、选择题（每小题5分，共25分）

1. 下列式子中符合代数式的书写格式的是（ ）

A. x·1

2y

B.m?3n C.x?y

4 D.23

4ab

2. 一个长方形的周长是45cm，一边长acm，这个长方形的面积为（ ）cm2

A.a(45?a)

2

22 B.45a2 C.(452?a) D.a(452?a) 3. 代数式x-7y用语言叙述为（ ）

A.x与7y的平方差 B.x的平方减7的差乘以y的平方

C.x与7y的差的平方 D. x的平方与y的平方的7倍的差

4. 当a=-2,b=4时，代数式(a?b)(a?ab?b)的值是（ ）

A.56 B.48 C. –72 D.72

5. 一个正方体的表面积为54 cm2，它的体积是（ ）cm3

A. 27 B.9 C.

三、解答题（每题10分，共50分）

第 3 页 共 5 页 22278 D. 36

代数式 代数式典型练习题

1. 列代数式

⑴ 若一个两位数十位上的数是a，个位上的数是b，这个两位数是_________.

若一个三位数百位上的数为a,十位上的数是b，个位上的数c，这个三位数是_________.

⑵ 某品牌服装以a元购进，加20%作为标价.由于服装销路不好，按标价的八五折出售，降价后的售价是__________元，这时仍获利________________________元.

⑶电影院第一排有a个座位，后面每排比前一排多2个座位，则第x排的座位有____________个.

⑷A、B两地相距s千米，某人计划a小时到达，如果需要提前2小时到达，每小时需多走___________________千米.

2. 已知代数式x2?x?3的值为7，求代数式3x2?3x?7的值. 3. 当

4. 若x?1?(y?3)?0，求1?xy?xy2的值 .5. 如图，大正方形边长为a，小正方形边长为b，求阴影部分的面积。［www.61k.com）

补充内容：

1、 已知2x2?xy?10,3y2?2xy?6， 2、如果关于字母x的代数式?3x2?mx?nx2?x?10

求4x?8xy?9y的值； 的值与x的取值无关，求m、n值。

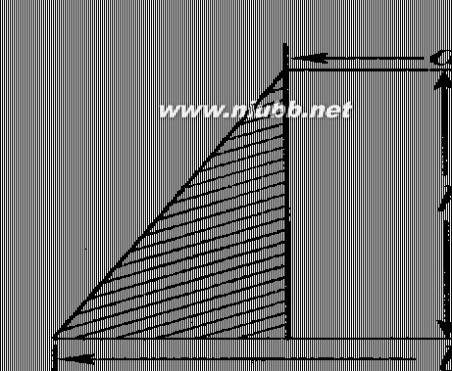
3、(1)用代数式表示图中阴影部分的面积S．(2)请你求出当a=2，b=5，h=4时，S的值．

4、问题：你能比较两个数2006

形式，即比较nn?1n22a?ba?b?14时，求代数式2(a?b)a?b?a?ba?b的值. 22007与20072006的大小吗？为了解决问题，首先把它抽象成数学问题，写出它的一般与(n?1)的大小（n是正整数），然后，从分析n?1，n?2，n?3，?，这些简单情形入手，从中发现规律，经过归纳，猜想出结论。

（1）通过计算，比较下列各组中两个数的大小（填“＞”，“＜”，“＝”）

①1221 ； ②233③343 ； ④455⑤56 ； ??

（2）从第（1）题的结果经过归纳，可以猜想出nn?124465与(n?1)的大小关系是2007n（3）根据上面的归纳猜想得到的一般结论，试比较下面两个数的大小：2006

第 4 页 共 5 页

2007

200

代数式 代数式典型练习题

强化练习参考答案

一、1.2a与b的差 2.⑴(1+10%)x ⑵(a+b)2 +(a-b)2 3. 2.1+0.3n 5.1 4.1.6+0.5(n-2) 5.n2+n=n(n+1) 6.10(a-3)+a 25

二、1.D 2.C3.C 4.A 5.B 三、1. ∵3a2-2a +6=8 2. b2-4ac=(- ∴ 3a2-2a=2 ∵(±

∴

∴

3232a

2

1

252

)2-4×(-1)×)2=

25452

32

=

254

的平方.

?a?1 ∴

254

是±

a?a?1?1?1?2.

2

3. ⑴b=0.8(220-14)=164.8

答：正常情况下,在运动时一个14岁的少年所能承受的每分钟心跳的最高次数164次. ⑵b=0.8(220-45)=140, ∵22×6=132 132＜140 ∴他没有危险. 单元检测参考答案

一、１．(1-20%)m 2．答案不唯一 ３．二、１C ２D ３B ４C ５A

三、1．⑴ 10a+b,100a+10b+c ⑵ (1+20%)a·85%,0.2a ⑶ a+(x-1) ⑷ (

sa?2

?sa

8a?b

(a?b)h

2

４．

，9cm2 ５．15

) ２．19 ３．-3.5 ４. -5 ５．4.

第 5 页 共 5 页

三 : 代数式典型练习题

第三讲：代数式同步练习及单元检测

课标要求

1.掌握用字母表示数，建立符号意识.

2.会列代数式表示简单的数量关系，会正确书写代数式，会求代数式的值.

3.在数学活动中，体会抽象概括的数学思想方法和“特殊?一般”相互转化的辨证关系.

典型例题

例1 某市出租车收费标准为：起步价5元，3千米后每千米价1.2元，则乘坐出租车走x(x﹥3)千米应付_______元.

例2 下列代数式中，书写正确的是（ ）

A. ab·2 B. a÷4 C. -4×a×b D. 3

例3 下列各题中，错误的是（ ）

A、代数式x2?y2的意义是x,y的平方和. B、代数式5(x+y)的意义是5与(x+y)的积

C、x 的5倍与y的和的一半，用代数式表示为5x?y

212xy E. 53mn F. -3×6 D、比x的2倍多3的数，用代数式表示为2x+3

友情提示：数学语言有文字语言、符号语言、图形语言.进行数学思维时，同学们要学会恰当使用各种语言推理分析，各种语言的互译是一种数学基本功.

例4 当x=1时，代数式px3?qx?1的值为2005，求x=－1时，代数式px3?qx?1 的值.

分析：当x=1时，px3?qx?1=p?q?1?2005，p+q=2004,

当x=－1时，px3?qx?1=－p?q?1?－（p+q）+1=－2004+1=－2003.

解：

提示：“整体”思想在数学解题中经常用到，请同学们在解题时恰当使用.

例5 下图是一个数值转换机的示意图，请你用x、y表示输出结果，并求输入x

的值为3，y的值为-2时的输出结果.

解：

提示：把图形语言翻译为符号语言的关键是识图，弄清图中运算顺序.

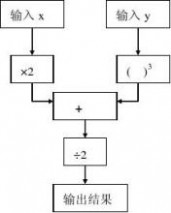
第 1 页 共 5 页

例6

例7：观察：2=1×2，2+4=2×3，2+4+6=3×4，?，试推算2+4+6+?+2n的公式，并利用推算公式计算100+102+?+200．

强化练习

一、填空题

1. 代数式2a-b表示的意义是_____________________________.

2. 列代数式：⑴设某数为x,则比某数大20%的数为__________.⑵a、b两数的和的平方与它们差的平方和__________.

3. 有一棵树苗，刚栽下去时，树高2.1米，以后每年长0.3米，则n年后的树高为_____，计算10年后的树高为___米.

4. 某音像社对外出租光盘的收费方法是：每张光盘在出租后的头两天每天收0.8元，以后每天收0.5元，那么一张光盘在出租后第n天（n＞2的自然数）应收租金_________________________元.

5. 观察下列各式：12+1=1×2，22+2=2×3，32+3=3×4------请你将猜想到的规律用自然数n(n≥1)表示出来______________________.

6. 一个两位数，个位上的数是a，十位上的数字比个位上的数小3，这个两位数为______，当a=5时，这个两位数为______.

二、选择题

1. 某品牌的彩电降价30%以后，每台售价为a元，则该品牌彩电每台原价为（ ）

A. 0.7a元 B.0.3a元 C.10

3a 元 D. 10

7a元

2. 根据下列条件列出的代数式，错误的是（ ）

A. a、b两数的平方差为a2-b2 B. a与b两数差的平方为(a-b)2

C. a与b的平方的差为a2-b2 D. a与b的差的平方为(a-b)2

3. 如果a?2?(b?1)?0,那么代数式(a+b)2005的值为（ ） 2

A. –2005 B. 2005 C. -1 D. 1

4. 笔记本每本m元，圆珠笔每支n元，买x本笔记本和y支圆珠笔，共需（ ）

A. （ mx+ny）元 B. (m+n)(x+y) C. （nx+my ）元 D. mn(x+y) 元

5. 当x=-2,y=3时,代数式4x-2y的值为（ ） A. 14 B. –50 C. –14 D. 50

三、解答题

第 2 页 共 5 页 32

1. 已知代数式3a-2a+6的值为8, 求23

2a?a?1的值. 2. 当a=-1,b=-212,c=11

2时，求代数式b-4ac的值，2

并指出求得的这个值是哪些数的平方.

3. 人在运动时的心跳速率通常和人的年龄有关.如果用a表示一个人的年龄，用b表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数，那么b=0.8(220-a).

⑴ 正常情况下,在运动时一个14岁的少年 ⑵ 一个45岁的人运动时10秒心跳的

所能承受的每分钟心跳的最高次数是多少？ 次数为22次，请问他有危险吗？为什么？

单元检测

一、填空题（每小题5分，共25分）

1. 某机关原有工作人员m人，现精简机构，减少20%的工作人员，则剩下_____人.

2. 结合生活经验作出具体解释：a-b__________________________________.

3. 甲以a千米/小时、乙以b千米/小时（a＞b）的速度沿同一方向前进，甲在乙的后面8千米处开始追乙，则甲追上

乙需_____________小时.

4. 若梯形的上底为a，下底为b，高为h，则梯形的面积为____________;当a=2cm，b=4cm，h=3cm时，梯形的面积

为____________.

5. 按下列程序计算x=3时的结果__________.

二、选择题（每小题5分，共25分）

1. 下列式子中符合代数式的书写格式的是（ ）

A. x·1

2y

B.m?3n C.x?y

4 D.23

4ab

2. 一个长方形的周长是45cm，一边长acm，这个长方形的面积为（ ）cm2

A.a(45?a)

2

22 B.45a2 C.(452?a) D.a(452?a) 3. 代数式x-7y用语言叙述为（ ）

A.x与7y的平方差 B.x的平方减7的差乘以y的平方

C.x与7y的差的平方 D. x的平方与y的平方的7倍的差

4. 当a=-2,b=4时，代数式(a?b)(a?ab?b)的值是（ ）

A.56 B.48 C. –72 D.72

5. 一个正方体的表面积为54 cm2，它的体积是（ ）cm3

A. 27 B.9 C.

三、解答题（每题10分，共50分）

第 3 页 共 5 页 22278 D. 36

1. 列代数式

⑴ 若一个两位数十位上的数是a，个位上的数是b，这个两位数是_________.

若一个三位数百位上的数为a,十位上的数是b，个位上的数c，这个三位数是_________.

⑵ 某品牌服装以a元购进，加20%作为标价.由于服装销路不好，按标价的八五折出售，降价后的售价是__________元，这时仍获利________________________元.

⑶电影院第一排有a个座位，后面每排比前一排多2个座位，则第x排的座位有____________个.

⑷A、B两地相距s千米，某人计划a小时到达，如果需要提前2小时到达，每小时需多走___________________千米.

2. 已知代数式x2?x?3的值为7，求代数式3x2?3x?7的值. 3. 当

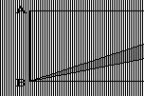
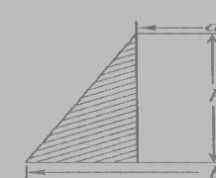
4. 若x?1?(y?3)?0，求1?xy?xy2的值 .5. 如图，大正方形边长为a，小正方形边长为b，求阴影部分的面积。

补充内容：

1、 已知2x2?xy?10,3y2?2xy?6， 2、如果关于字母x的代数式?3x2?mx?nx2?x?10

求4x?8xy?9y的值； 的值与x的取值无关，求m、n值。

3、(1)用代数式表示图中阴影部分的面积S．(2)请你求出当a=2，b=5，h=4时，S的值．

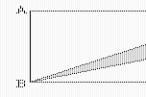
4、问题：你能比较两个数2006

形式，即比较nn?1n22a?ba?b?14时，求代数式2(a?b)a?b?a?ba?b的值. 22007与20072006的大小吗？为了解决问题，首先把它抽象成数学问题，写出它的一般与(n?1)的大小（n是正整数），然后，从分析n?1，n?2，n?3，?，这些简单情形入手，从中发现规律，经过归纳，猜想出结论。

（1）通过计算，比较下列各组中两个数的大小（填“＞”，“＜”，“＝”）

①1221 ； ②233③343 ； ④455⑤56 ； ??

（2）从第（1）题的结果经过归纳，可以猜想出nn?124465与(n?1)的大小关系是2007n（3）根据上面的归纳猜想得到的一般结论，试比较下面两个数的大小：2006

第 4 页 共 5 页

2007

200

强化练习参考答案

一、1.2a与b的差 2.⑴(1+10%)x ⑵(a+b)2 +(a-b)2 3. 2.1+0.3n 5.1 4.1.6+0.5(n-2) 5.n2+n=n(n+1) 6.10(a-3)+a 25

二、1.D 2.C3.C 4.A 5.B 三、1. ∵3a2-2a +6=8 2. b2-4ac=(- ∴ 3a2-2a=2 ∵(±

∴

∴

3232a

2

1

252

)2-4×(-1)×)2=

25452

32

=

254

的平方.

?a?1 ∴

254

是±

a?a?1?1?1?2.

2

3. ⑴b=0.8(220-14)=164.8

答：正常情况下,在运动时一个14岁的少年所能承受的每分钟心跳的最高次数164次. ⑵b=0.8(220-45)=140, ∵22×6=132 132＜140 ∴他没有危险. 单元检测参考答案

一、１．(1-20%)m 2．答案不唯一 ３．二、１C ２D ３B ４C ５A

三、1．⑴ 10a+b,100a+10b+c ⑵ (1+20%)a·85%,0.2a ⑶ a+(x-1) ⑷ (

sa?2

?sa

8a?b

(a?b)h

2

４．

，9cm2 ５．15

) ２．19 ３．-3.5 ４. -5 ５．4.

第 5 页 共 5 页

本文标题：代数式练习题-代数式经典练习题
本文地址： http://www.61k.com/1141823.html