一 : 成考数学选择题怎么考40分

成考数学选择题怎么考40分

成考数学选择题怎么考40分的参考答案

背公式.多做题,

二 : 2013高考数学选择题已知点A(-1，0)，B(1，0),C(0

2013高考数学选择题

已知点A(-1，0)，B(1，0),(0，1),直线y=ax+b（a大于0），将三角形ABC分割为面积相等的两部分，则b的取值范围是？

---

这是哪个省的高考题，题目很灵活，好

三 : 2014年高考数学经典选择题

2014年数学高考经典选择题

1. 设f(x)的定义域为D，若f(x)满足下面两个条件则称f(x)为闭函数：①f(x)是D上单调函数；②存在[a,b]?D，使f(x)在[a,b]上值域为[a,b].

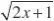
现已知

f(x)??k为闭函数，则k的取值范围是（ ）

A

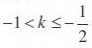
．k?1 C

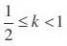
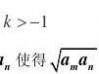
2.已知正项等比数列{an}满足a7?a6?2a5。若存在两项am,?4a1，则

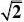
19?的最小值为( )

mn

A 8111417 B C D 3456

3.平面四边形ABCD中，,且AD?AB，现将?ABD沿着对角线

BD翻折成?A/BD，则在?A/

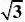
BD折起至转到平面BCD内的过程中，直线A/C与平面BCD所成的最大角的正切值为( )

A 1 B 1 C 32

4.已知f(x)、g(x)都是定义在R上的函数，g(x)?0，f?(x)g(x)?f(x)g?(x)，f(x)?

axg(x)，5f(1)f(?1)5??，则关于x的方程abx2???0(b?(0,1))有2g(1)g(?1)2

2 53 5两个不同实根的概率为（ ） A1 5BCD4 5

时，0,1]5.已知f(x)是定义在[?1,1]上的奇函数，当x1?x2时，f(x1)?f(x2)。当x?[x2f()?f(x),f(x)?1?f(1?x)，则 5

f(? 150151170171)?f(? )???f(? )+f(? )?( ) 2014201420142014

A ?

1127B?5 C?6 D? 52

6. 平面?外有两条直线m和n，如果m和n在平面?内的射影分别是m1和n1，给出下列四个命题：①m1?n1?m?n ②m?n?m1?n1 ③m1与n1相交?m与n相交或重合 ④m1与n1平行?m与n平行或重合，其中不正确的命题的个数是（ ）

A.4个 B.3个 C .2个 D. 1

7．已知方程组??x?2y?z?2u对此方程组的每一组正实数解(x,y,z,u)，其中z?y，都2yz?ux?

存在正实数M，且满足M?

A. 1

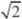
z，则 M的最大值是 （ ） yC .6?

D. 3? B. 3?

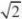
8．已知函数f(x)??

围是（ ） ?0,x?0?e,x?0x，则使函数g(x)?f(x)?x?m有零点的实数m的取值范

A. [0,1) B.(??,1)

C. (??,0]?(1,??) D. (??,1]?(2,??)

9．若某棱锥的三视图(单位：cm)如图所示，

则该棱锥的体积等于（ ）

A．10 cm B．20 cm

C．30 cm D．40 cm

3333

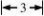
俯视图

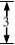
(8题图)

10. 若抛物线y?4x的焦点是F，准线是l，点M（4，4）是抛物线上一点，则经过点F、 2

M且与l相切的圆共有（ ）

A．0个 B．1个 C．2个 D．4个

11．中心在原点，焦点在x轴上的双曲线C的离心率为2，直线l与双曲线C交于A,B两 点，线段AB中点M在第一象限，并且在抛物线y?2px?p?0?上，且M到抛物线焦点2

的距离为p，则直线l的斜率为（ ）

A．1

12．把曲线C：y?Ｂ． 2 Ｃ．3 2Ｄ．5 27???x)?cos(x?)的图像向右平移a(a?0)个单位，得到曲线C?88

?2b?13b?2的图像，且曲线C?的图像关于直线x?对称，当x?[时，?,?]（b为正整数）488

过曲线C?上任意两点的斜率恒大于零，则b的值为（ ）

A．1 Ｂ． 2 Ｃ．3

Ｄ．4

?x?016?1．已知x，y满足约束条件?3x?4y?4,则x2?y2的最小值是 25?y?0?

2.数列{an}的首项为1，数列{bn}为等比数列且bn?

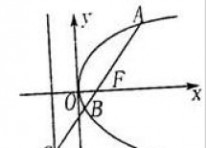
2an?1，若b10?b11?2，则a21?1024 an3．如图，过抛物线y?2px(p?0)的焦点F的直线l依次交抛物线及

其准线于点A、B、C，若|BC|=2|BF|，且|AF|=3，则抛物线的方程是

4.已知正四面体ABCD的棱长为1，M为AC的中点，P在线段DM上，则(AP?BP)的最小值为_____________

；1?2 3

5.已知偶函数f(x)满足对任意x?R，均有f(1?x)?f(3?x)且

?m(1?x2),x?[0,1]f(x)??，若方程3f(x)?x恰有5个实数解，则实数m的取值范围x?1,x?(1,2]?

是_______.4884?m?或??m?? 3333

6.已知平行六面体ABCD?A1B1C1D1，AC1与平面A1BD，CB1D1交于E,F两点。给出以下命题，其中真命题有________(写出所有正确命题的序号) ①⑤

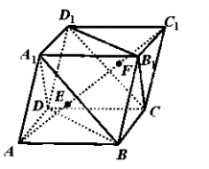
①点E,F为线段AC1的两个三等分点； ??????1?????2????1???②ED1??DC?AD?AA1； 333

③设A1D1中点为M，CD的中点为N，则直线MN与面A1DB有一个交点； ④E为?A1BD的内心；

⑤设K为?B1CD1的外心，则VK?BED为定值. VA1?BFD

7. 若正数x,y满足2x?y?3?0，则x?2y的最小值为 ．3 xy

8．有6名同学参加两项课外活动，每位同学必须参加一项活动且不能同时参加两项，每项活动最多安排4人，则不同的安排方法有_____种．（用数字作答）50

y2x2

9．若F1,F2分别为双曲线2?2?1的下，上焦点，O为坐标原点，点P在双曲线的下支ab

??????????????????????F1PF1O上，点M在上准线上，且满足F2O?MP,F1M??(?)(??0)，则双曲线F1PF1O

的离心率__________.2

10.如图，已知球O是棱长为1的正方体ABCD?A1B1C1D1

的内切球，则平面ACD1截球O的截面面积为．? 6

11. 设函数f(x)的定义域为D，如果存在正实数k，使对任意x?D，都有x+k?D，且

f(x+k)>f(x) 恒成立，则称函数f(x)为D上的“k型增函数”。已知f(x)是定义在R上的

?

1007 3

四 : 2014年高考数学经典选择题

2014年数学高考经典选择题

1. 设f(x)的定义域为D，若f(x)满足下面两个条件则称f(x)为闭函数：①f(x)是D上单调函数；②存在[a,b]?D，使f(x)在[a,b]上值域为[a,b].

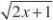
现已知

f(x)??k为闭函数，则k的取值范围是（ ）

A

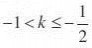
．k?1 C

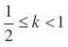
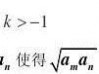
2.已知正项等比数列{an}满足a7?a6?2a5。（www.61k.com］若存在两项am,?4a1，则

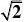
19?的最小值为( )

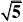
mn

A 8111417 B C D 3456

3.平面四边形ABCD中，,且AD?AB，现将?ABD沿着对角线

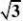
BD翻折成?A/BD，则在?A/

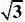
BD折起至转到平面BCD内的过程中，直线A/C与平面BCD所成的最大角的正切值为( )

A 1 B 1 C 32

4.已知f(x)、g(x)都是定义在R上的函数，g(x)?0，f?(x)g(x)?f(x)g?(x)，f(x)?

axg(x)，5f(1)f(?1)5??，则关于x的方程abx2???0(b?(0,1))有2g(1)g(?1)2

2 53 5两个不同实根的概率为（ ） A1 5BCD4 5

时，0,1]5.已知f(x)是定义在[?1,1]上的奇函数，当x1?x2时，f(x1)?f(x2)。当x?[x2f()?f(x),f(x)?1?f(1?x)，则 5

f(? 150151170171)?f(? )???f(? )+f(? )?( ) 2014201420142014

A ?

1127B?5 C?6 D? 52

高考数学选择题 2014年高考数学经典选择题

6. 平面?外有两条直线m和n，如果m和n在平面?内的射影分别是m1和n1，给出下列四个命题：①m1?n1?m?n ②m?n?m1?n1 ③m1与n1相交?m与n相交或重合 ④m1与n1平行?m与n平行或重合，其中不正确的命题的个数是（ ）

A.4个 B.3个 C .2个 D. 1

7．已知方程组??x?2y?z?2u对此方程组的每一组正实数解(x,y,z,u)，其中z?y，都2yz?ux?

存在正实数M，且满足M?

A. 1

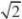
z，则 M的最大值是 （ ） yC .6?

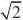
D. 3? B. 3?

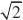
8．已知函数f(x)??

围是（ ） ?0,x?0?e,x?0x，则使函数g(x)?f(x)?x?m有零点的实数m的取值范

A. [0,1) B.(??,1)

C. (??,0]?(1,??) D. (??,1]?(2,??)

9．若某棱锥的三视图(单位：cm)如图所示，

则该棱锥的体积等于（ ）

A．10 cm B．20 cm

C．30 cm D．40 cm

3333

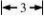
俯视图

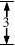
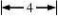
(8题图)

高考数学选择题 2014年高考数学经典选择题

10. 若抛物线y?4x的焦点是F，准线是l，点M（4，4）是抛物线上一点，则经过点F、 2

M且与l相切的圆共有（ ）

A．0个 B．1个 C．2个 D．4个

11．中心在原点，焦点在x轴上的双曲线C的离心率为2，直线l与双曲线C交于A,B两 点，线段AB中点M在第一象限，并且在抛物线y?2px?p?0?上，且M到抛物线焦点2

的距离为p，则直线l的斜率为（ ）

A．1

12．把曲线C：y?Ｂ． 2 Ｃ．3 2Ｄ．5 27???x)?cos(x?)的图像向右平移a(a?0)个单位，得到曲线C?88

?2b?13b?2的图像，且曲线C?的图像关于直线x?对称，当x?[时，?,?]（b为正整数）488

过曲线C?上任意两点的斜率恒大于零，则b的值为（ ）

A．1 Ｂ． 2 Ｃ．3

Ｄ．4

?x?016?1．已知x，y满足约束条件?3x?4y?4,则x2?y2的最小值是 25?y?0?

2.数列{an}的首项为1，数列{bn}为等比数列且bn?

2an?1，若b10?b11?2，则a21?1024 an3．如图，过抛物线y?2px(p?0)的焦点F的直线l依次交抛物线及

其准线于点A、B、C，若|BC|=2|BF|，且|AF|=3，则抛物线的方程是

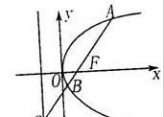
高考数学选择题 2014年高考数学经典选择题

4.已知正四面体ABCD的棱长为1，M为AC的中点，P在线段DM上，则(AP?BP)的最小值为_____________

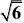
；1?2 3

5.已知偶函数f(x)满足对任意x?R，均有f(1?x)?f(3?x)且

?m(1?x2),x?[0,1]f(x)??，若方程3f(x)?x恰有5个实数解，则实数m的取值范围x?1,x?(1,2]?

是_______.4884?m?或??m?? 3333

6.已知平行六面体ABCD?A1B1C1D1，AC1与平面A1BD，CB1D1交于E,F两点。［www.61k.com）给出以下命题，其中真命题有________(写出所有正确命题的序号) ①⑤

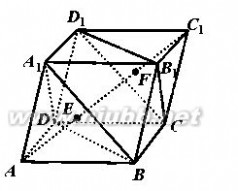
①点E,F为线段AC1的两个三等分点； ??????1?????2????1???②ED1??DC?AD?AA1； 333

③设A1D1中点为M，CD的中点为N，则直线MN与面A1DB有一个交点； ④E为?A1BD的内心；

⑤设K为?B1CD1的外心，则VK?BED为定值. VA1?BFD

高考数学选择题 2014年高考数学经典选择题

7. 若正数x,y满足2x?y?3?0，则x?2y的最小值为 ．3 xy

8．有6名同学参加两项课外活动，每位同学必须参加一项活动且不能同时参加两项，每项活动最多安排4人，则不同的安排方法有_____种．（用数字作答）50

y2x2

9．若F1,F2分别为双曲线2?2?1的下，上焦点，O为坐标原点，点P在双曲线的下支ab

??????????????????????F1PF1O上，点M在上准线上，且满足F2O?MP,F1M??(?)(??0)，则双曲线F1PF1O

的离心率__________.2

10.如图，已知球O是棱长为1的正方体ABCD?A1B1C1D1

的内切球，则平面ACD1截球O的截面面积为．? 6

11. 设函数f(x)的定义域为D，如果存在正实数k，使对任意x?D，都有x+k?D，且

f(x+k)>f(x) 恒成立，则称函数f(x)为D上的“k型增函数”。（www.61k.com)已知f(x)是定义在R上的

?

1007 3

五 : 数学选择

1在空间直角坐标系中，与点（3,1,7）关于x0y面对称的点是--（3,1，-7）
2在空间直角坐标系中，和点（3,1,2）关于ox轴对称的点是--（3，-1，-2）
3下列各点在zox面上的点是--（2,0,3）
4点（a，b，c）到x轴的距离为--更号（b方+c方）
5向量a=-2i+3j+nk与B=mi-6j+2k平行，则m与n的取值应为--（m=4，n=-1）
6设a，b为非零向量，若axb=0，则--（a ll b）
7平面Ax+By+Cz+D=0过x轴则--（A=D=0)
8平面3x-5z+1=0--（平行于y轴）
9平面x-2y+3z-8=0与平面2x+y-3=0的位置关系--（垂直）
10直线l1；x-1=y=-（z+1）与l2；x=-（y-1）=（z+1）/0的位置关系是--（垂直）
11设空间直线的标准方程是x/0=y/1=z/2则该直线过原点，且--（垂直于x轴）
12方程 x方+y方+z方=0在空间直角坐标系表示--（一点）
13 lim下（x，y）-（0,0） xy/（x方+y方）--（不存在）
14函数z=f（x，y）在点（x0，y0）处连续是它在该点偏导数存在的--（既非充分又非必要条件）
15函数z=f（x，y）在点（x0，y0）处具有偏导数是它在该点存在全微分的--（必要而非充分条件）
16函数z=f（x，y）的二阶混合偏导数fxy（x，y）及fxy（x，y）在区域D内连续是在该区域D内fxy（x，y）=fyx（x，y）的--（充分而非必要条件）
17设函数z=1-更号（x方+y方）则点（0,0）是函数z的--（极大值点且是最大值点）
18fx（x0，y0）=0，fy（x0，y0）=0是可微函数f（x，y）在点（x0，y0)取得极值的--（必要而非充分条件）
19设函数z=f（x，y）具有二阶连续偏导数，在点P0（x0，y0）处----（点P0非函数z的极值点）
20函数f（x，y）=（6x-x方）（4y-y方）的驻点个数为---（5个）
21函数f（x，y）在有界闭域D上连续是二重积分[[f（x，y）d6存在的---（充分条件，但非必要条件）
22设I1=[[e的xy方d6，I2=[[e的2xy方d6，其中D是矩形区域{0,1}x{0,1}则I1与I2的大小关系是---（I1<I2)
23设积分区域D是矩形区域{0，派/4}x{0，派/4}，根据二重积分的估值不等式，----（p=0）
24二重积分I={上2下0 dx{上更号（4-x方）下0 （x方+y方）dy-----（{上派/2下0 d8{上2下0 r三次方dr）
25设级数西格玛（上无穷下n=1）an收敛，和为S-----（S-a1）
26下列命题中正确的是---（A un=0）
27下列命题不正确的是---（B 不一定发散）
28若级数西格玛（上无穷下n=1）a/q的n次方收敛，则q满足---（绝对的q>1）
29下列级数收敛的是---（A）
30设收敛级数西格玛（上无穷下n=1）Un的和为S,前n-1项，n项，n+1项----(D lim下n到无穷Sn+1不等S）
32设西格玛（上无穷下n=1）Un是正项级数----（C）
33函数项级数lnx+ln方x+---+ln方x+==的收敛域为---（1/e<x<e）
34设幂级数 西格玛（上无穷下n=1）anx的N次方当x=x0时收敛---（B)

本文标题：高考数学选择题-成考数学选择题怎么考40分
本文地址： http://www.61k.com/1136771.html