一 : 椭圆面积公式的推导
椭圆面积公式的推导
韩贞焱 (贵州省遵义四中 563000)
椭圆面积公式S=?ab(其中a、b分别是椭圆的长半轴、短半轴的长).在中学数学教材中,仅在高中《平面解析几何》的习题中作为已知公式给出过,直到高等数学的定积分学习时才给出定积分推导.现用初等数学方法作两种推导,供读者参考.
定理1. 若夹在两条平行直线间的两个平面图形,被平行于两条平行直线的任一直线所截,如果截得的两条线段长的比例总相等,那么这两个平面图形的面积比等于截得线段长的比 .
注:此定理相当于祖暅原理的推论,故证明从略.
x2y2方法一:设椭圆C的方程为2?2?1(a>b>0),辅助圆C'的方程ab
为x2+y2=b2,且一直线L:y = m(?b?m?b)与两曲线相交,交点分别为M(x1 , m)、 N(x2 , m)及P(x3 , m)、Q(x4, m),如图1. ?y?ma??b2?m2, 由?x2y2解得 x1、=2b?2?2?1b?a
此时,x1?x2 =2a2b?m2; b
?y?m22由?2 解得x=±, (图1)
b?m3,422?x?y?b
第 1 页
椭圆的面积公式 椭圆面积公式的推导
此时, x3?x4=2b2?m2.
10、当b2?m,即b=|m|时,交点为(0,b)或(0,-b); 2、当b?m,即b≠|m|时,有022x1?x2
x3?x4?a . b
显然10是一种特殊情况,即直线L与两曲线C、C' 交于一点,此时与求椭圆C的面积无影响,故可忽略;在情况20下,即椭圆C的弦长|MN|与圆C'的弦长|PQ|比恒为定值a时,则当设椭圆C与圆C'的面积分别为S、b
S'时,由定理1得
b2=πab . Saa'a''2=,又圆C的面积S=πb,故有 S =S=πbbS'b
所以椭圆C的面积公式为S =πab (其中a、b分别是椭圆的长半轴、短半轴的长).
注:此法适应于类似夹在两条平行直线间的平面图形,若被平行于两平行直线的任一条直线所截得的线段长成相等比例,当已知线段长的比值时,则可利用定理1由一已知平面图形面积求另一平面图形面积.
定理2.若一平面图形M'是另一凸平面图形M的射影,且凸平面图形M与射影平面图形M'所成角为?, 则射影平面图形M'的面积与凸平面图形M的面积比为cos?.
证明:设平面图形M'是平面图形M的射影 .10当平面图形M是凸
第 2 页
椭圆的面积公式 椭圆面积公式的推导
1'
曲边行时,如图2,将平面图形M的边缘进行n+1等分, 设分点分别为A1、A2、A3、…、Ai、Ai?1、 …、An 、An?1,它们分别在平
'
面图形M'上的射影为A1、A'2
…、Ai'、Ai'?1、…、A'n、A'n?1 , 则分别连结点A1、A2、A3、… 、Ai、Ai?1、…、An 、An?1,然 后再将点A1分别与点 A2、A3、
…、Ai、Ai?1、…、An 、An?1 (图2)
连结得△A1A2A3、△A1A3A4、…△A1AiAi?1、…、△A1AnAn?1.显然
''''它们在平面图形M' 上的射影分别是对应的△A1A'2A3、△A1A3A'4、…、''△A1Ai'Ai'?1、…、△A1A'nA'n?1 由于平面M与平面M'所成角为?,则
△A1A2A3、△A1A3A4、…、△A1AiAi?1、…、△A1AnAn?1 所在平
''''''面与△A1A'2A3、△A1A3A'4、…、△A1Ai'Ai'?1、…、△A1A'nA'n?1 所
在平面所成角均为?,现分别记△A1A2A3、△A1A3A4、…、△
''''A1AiAi?1、…、△A1AnAn?1 及△A1A'2A3、△A1A3A'4、…、△'''A1Ai'Ai'?1、…、△A1A'n A'n?1 的面积为S1 、S2、…、Si、…、Sn及 S1、
S'2、…、Si'、…、S'n. 则有S= S1con? 、S'2 = S2 con?、…、 Si'= Sicon?、…、S'n = Sncos? .
' 当分点无限增加时, 则S1 、S2、…、Si、…、Sn 及S1、S'2、…、
第 3 页
椭圆的面积公式 椭圆面积公式的推导
Si'、…、S'
n 的和就分别无限地接近凸曲边形M的面积和射影平面图形M'的面积, 故有
' S'=lim( S1 +S'
2 +…+Si' +…+S'
n) n??
=lim( S1cos? + S2 cos?+…Si+cos?+…+Sncos?) n??
=lim( S1 +S2+…+Si+…+Sn) cos? n??
=S cos?.
20当平面图形M是凸多边形时,则在凸多边形M内取适当的点连结出不重叠的三角形,仿上易证,故略 .
方法二:我们知道,在一
圆柱上作一斜截面可得一椭圆面,
如图3. 设圆柱oo1的底面直径
A B'=2 b, 斜截面椭圆的长轴长
A B =2a, 椭圆面M'与圆柱底面
M所成角为?,将椭圆周n+1等
'分,设其分点分别为P1、P'
2、…
、Pi'、Pi'?1、…、P'
n、P'
n?1, 在底 (图3)
面圆周上的 射影分别为P1、P2、…、Pi、Pi?1、…、Pn、Pn?1,分别连结
''点A、P1、P'
2;A、 P'
2、P3;、…;A、Pi'、Pi'?1;…;A 、 P'
n、P'
n?1及
点A、P1、P2;A、P2、P3;…;A、Pi、Pi?1;…; A、Pn、 Pn?1。(www.61k.com)设
第 4 页
椭圆的面积公式 椭圆面积公式的推导
椭圆面的面积及圆柱底面面积分别为 S'、S,因为圆柱底面面积S'=?b2.
aS'
且b =a cos?,则仿定理2可证 S= =? b2 =?ab . 故椭圆的面bcos?
积公式为 S=?ab . (其中a、b分别是椭圆的长半轴、短半轴的长).
注:此法还适应于可展为平面图形的曲面图形与其射影平面图形间,当已知一曲面图形形成的侧面母线与其射影平面图形所成定角的大小时,则可利用定理2由一已知图形面积求另一图形面积(如圆锥、圆台的侧面面积亦可由底面面积求得).
第 5 页
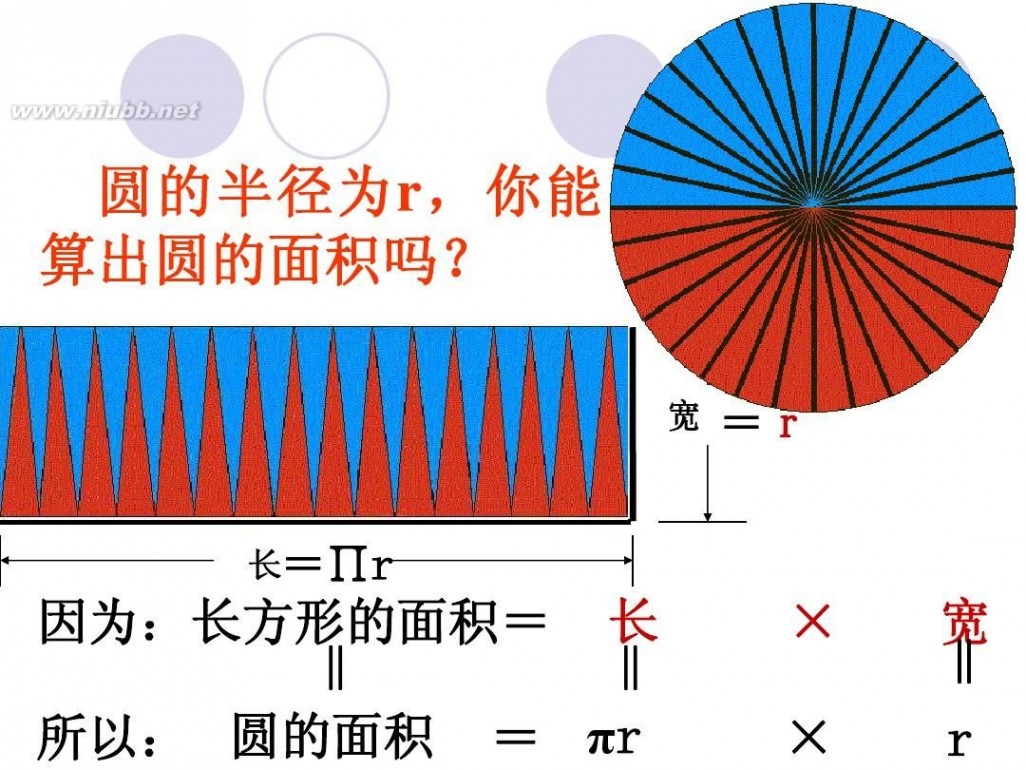
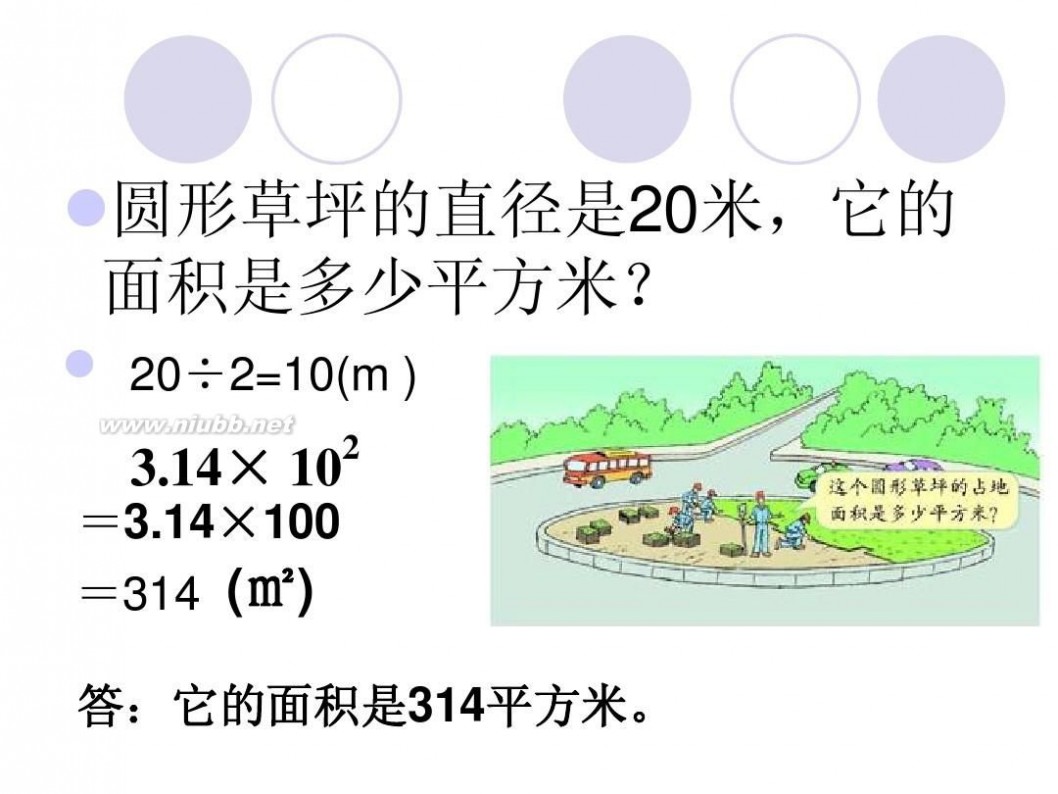
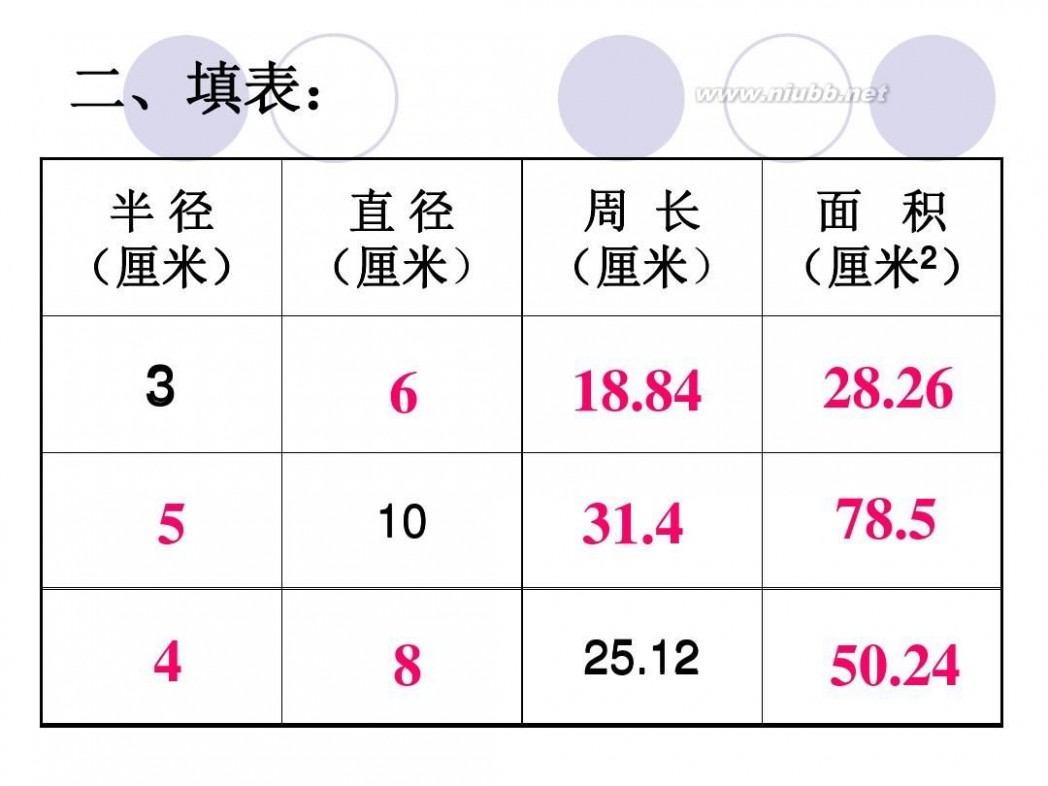
二 : 圆的面积公式是如何推导出来的?
网友蒙面大侠对[圆面积公式]圆的面积公式是如何推导出来的?给出的答复:
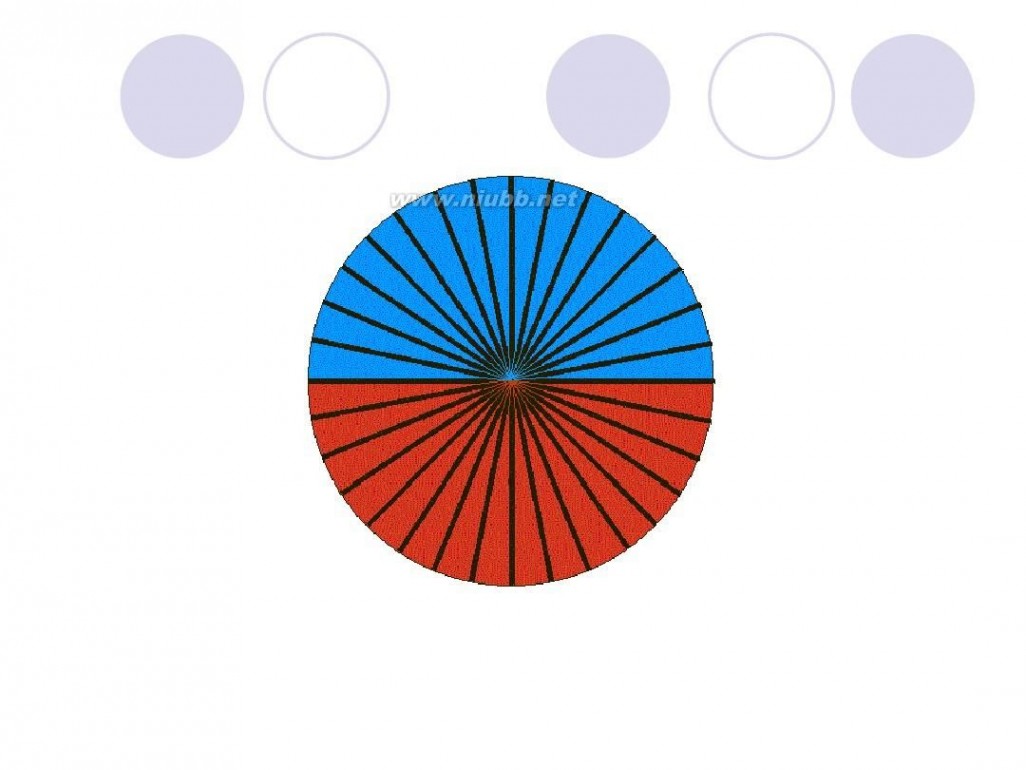
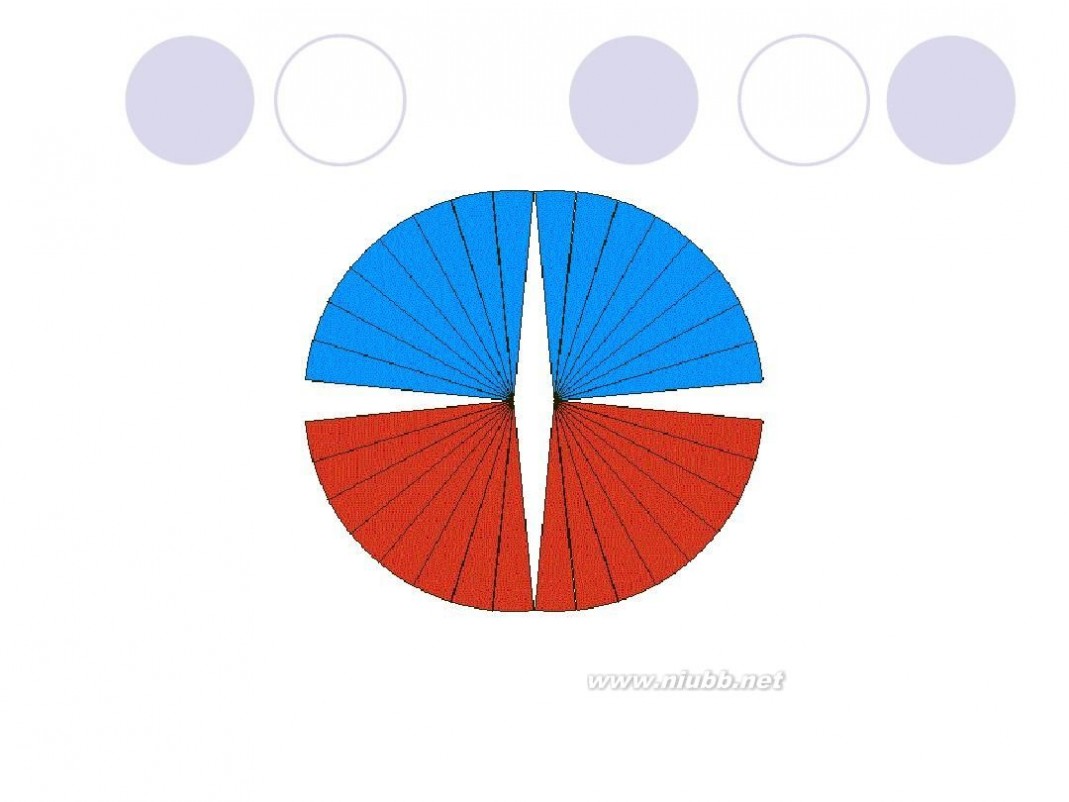
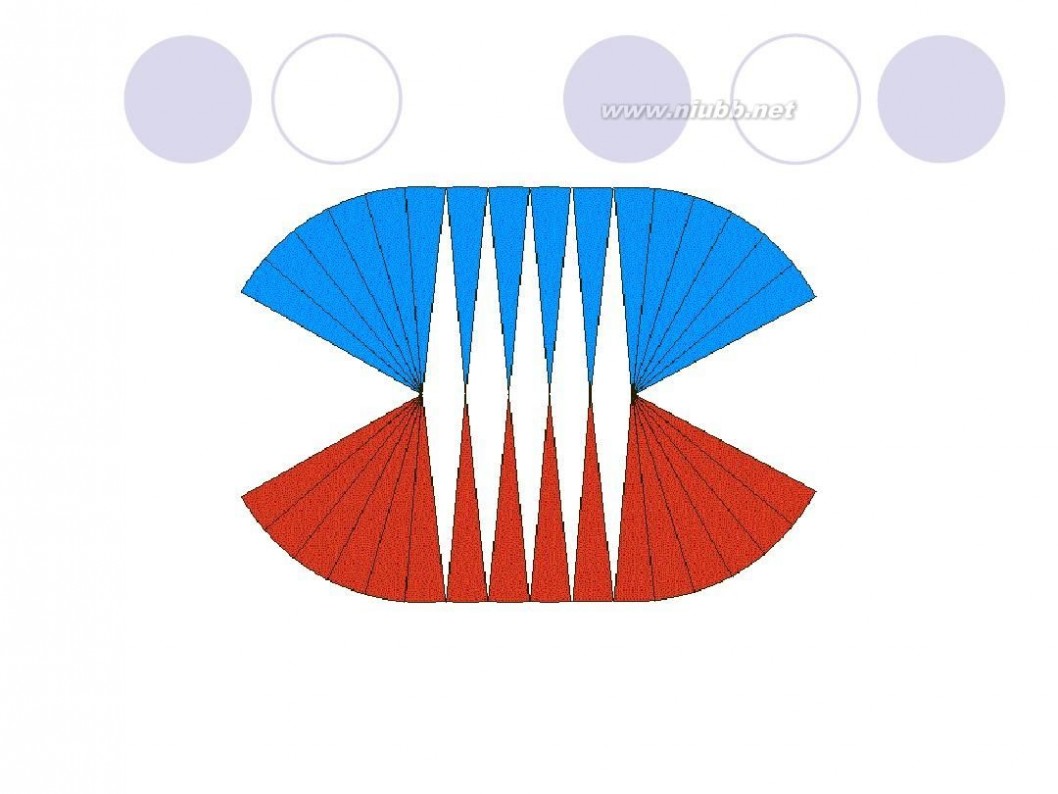
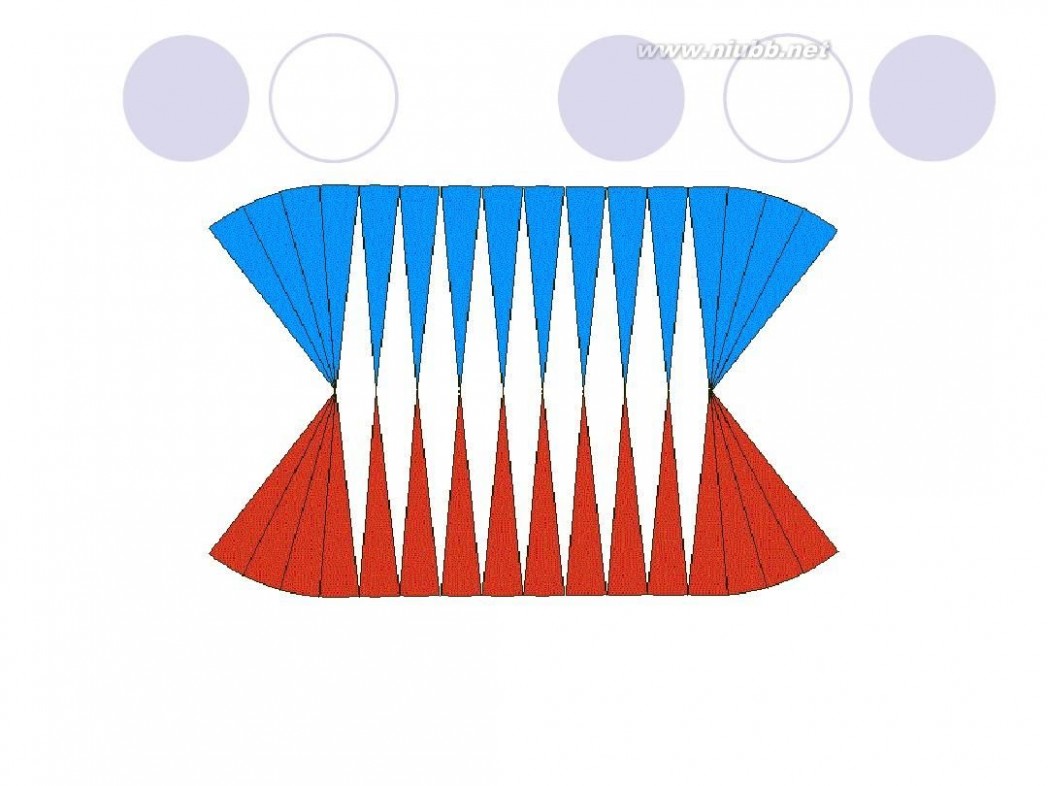
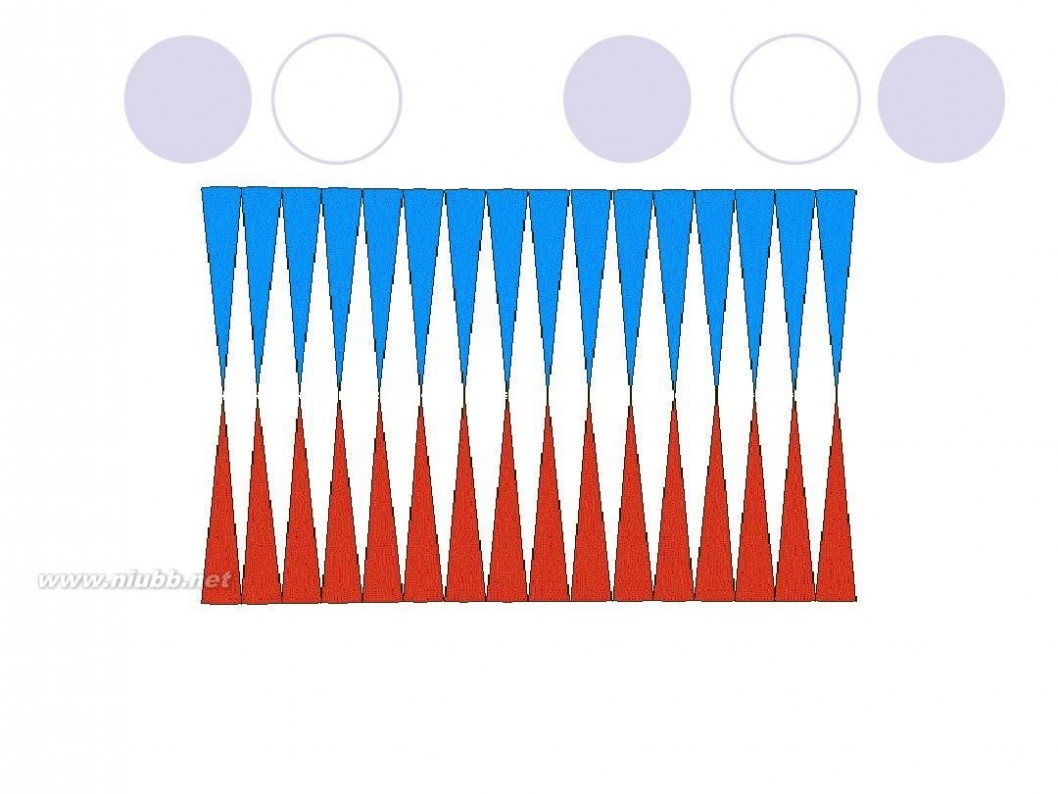
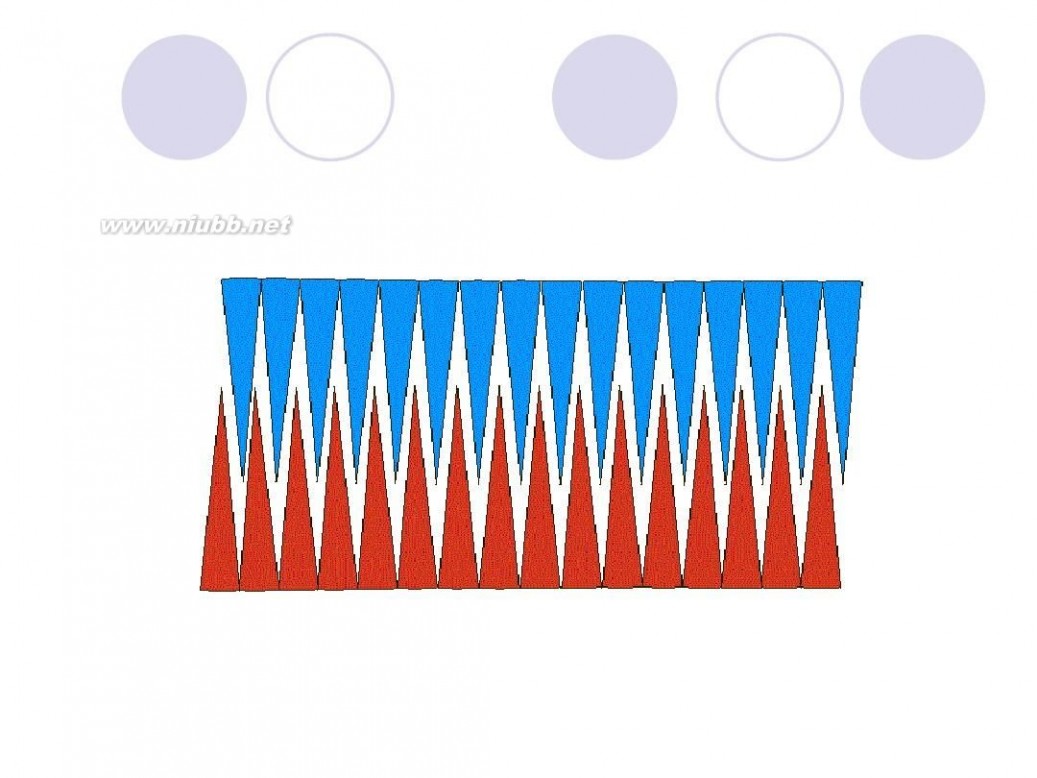
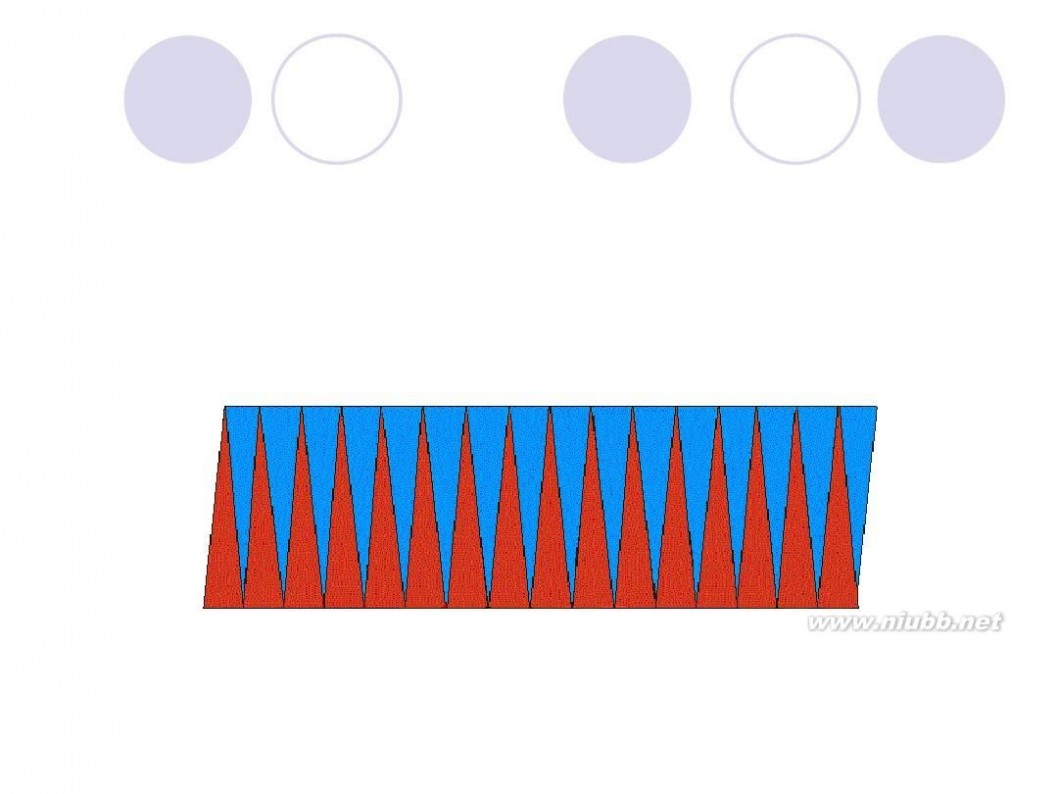
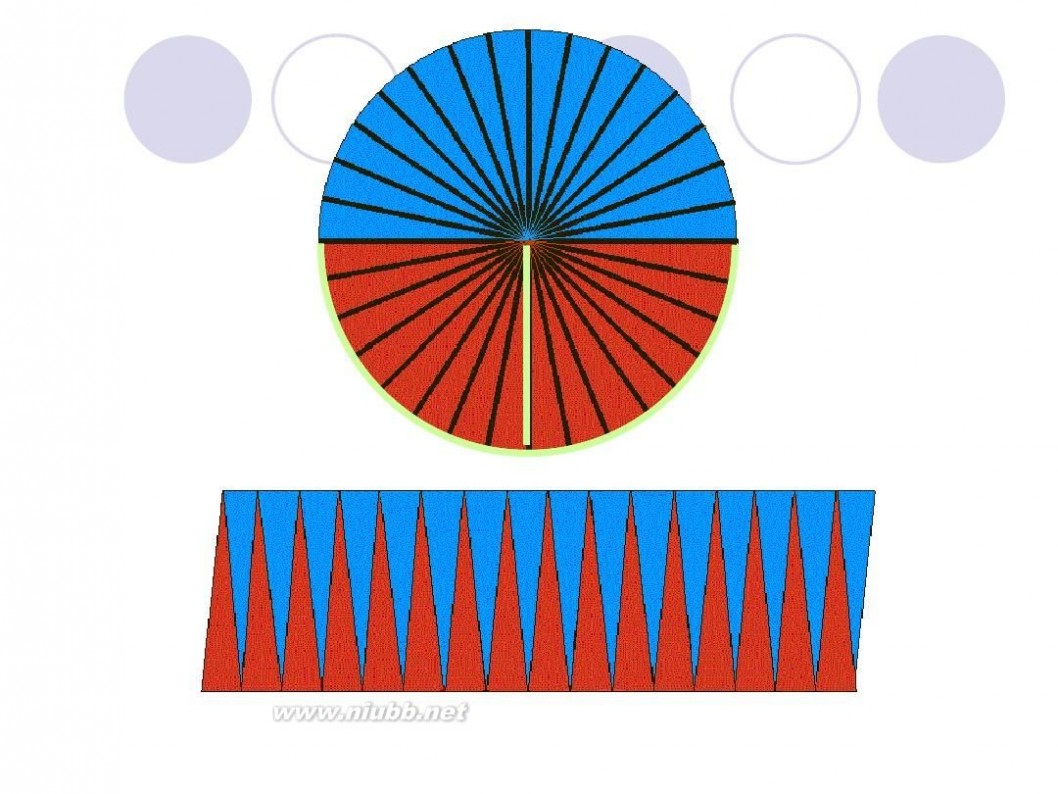
把圆用切蛋糕的方法切成无数多个小扇形,扇形的顶角无穷小,这时候可以近似认为扇形的曲线边是直线,近似认为扇形是等腰三角形,腰是半径,底边是很短很短的线段。把这些小三角形正一个倒一个的拼起来,就成了一个长方形啦~ 长方形的长为 圆周长的一半(因为有两条长边~),宽为圆的半径 面积相等,所以有 r*(r+6.42)=3.14*r*r 解方程就行了~ 或者由题设可列方程 3.14*r=r+6.42 两个方程都可以 ===========================================================
详情参考小学六年级课本,圆那一章,购书地址:http://product.dangdang.com/product.aspx?product_id=22807328
网友Snorri对[圆面积公式]圆的面积公式是如何推导出来的?给出的答复:
给一个不同的想法:
1.由于确定一个圆只需要圆心和半径,而圆心的位置和面积是没有关系的(图形的平移不变性),所以圆的面积应该是一个关于半径 r 的函数:S = S ( r )。
2.等比例的坐标放缩变换对一维对象的作用是等比放缩,对二维对象的作用是平方放缩,因此各种平面图形的面积S如果满足S = S (d1, d2, ... , dk),那么S (k.d1, k.d2, ... , k.dm) = k^2 . S (d1, d2, ... , dk). 所以圆的面积S ( r ) = r^2 S ( 1 ),它正比于r^2。
3.假设圆的面积S ( r ) = C r^2,那么考虑圆中一个扇形的面积。假设这个扇形的弧边长度是 ar,那么由于圆形的对称性,扇形的面积和整个圆形面积的比值应该等于弧长和圆周长的比值
S(扇形)/S(圆形) = ar/圆周长
4.在弧长趋于0的时候,可以将扇形看成是以弧长ar为高,半径 r 为底的三角形,面积约等于 ar^2/2,
所以a趋于0的时候,
ar^2/2Cr^2 ~ ar/圆周长
也就是说,圆周长/2r = C
所以C等于圆周率π。
网友匿名用户对[圆面积公式]圆的面积公式是如何推导出来的?给出的答复:
圆心在原点,半径为 的圆方程为
的圆方程为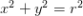
当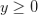 时,
时, 和
和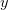 是一一对应关系,可以看出函数
是一一对应关系,可以看出函数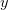
基本微积分知识告诉我们,当我们求积分 时,就是求半圆的面积,于是利用对称性,我们可知
时,就是求半圆的面积,于是利用对称性,我们可知
可以利用第一换元积分法等方法求出该积分的值,最后结果就是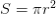
网友ssd swift对[圆面积公式]圆的面积公式是如何推导出来的?给出的答复:
圆面积 = (圆周/2) x 半径 = (π x 半径) x 半径 = π x 半径2
如下图所示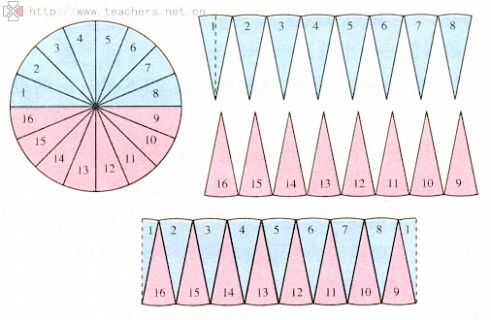
三 : 圆的面积公式是如何推导出来的?
【Snorri的回答(0票)】:四 : 椭圆面积公式的几种推导方法


五 : 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导
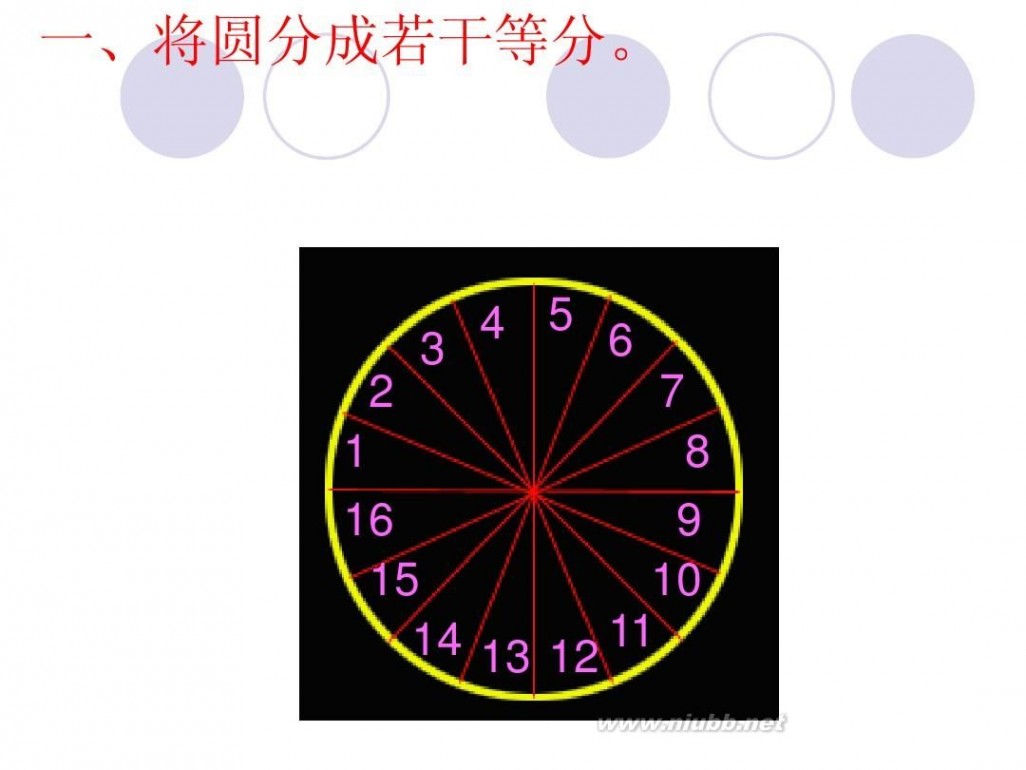
圆面积的推导过程 圆的面积公式推导
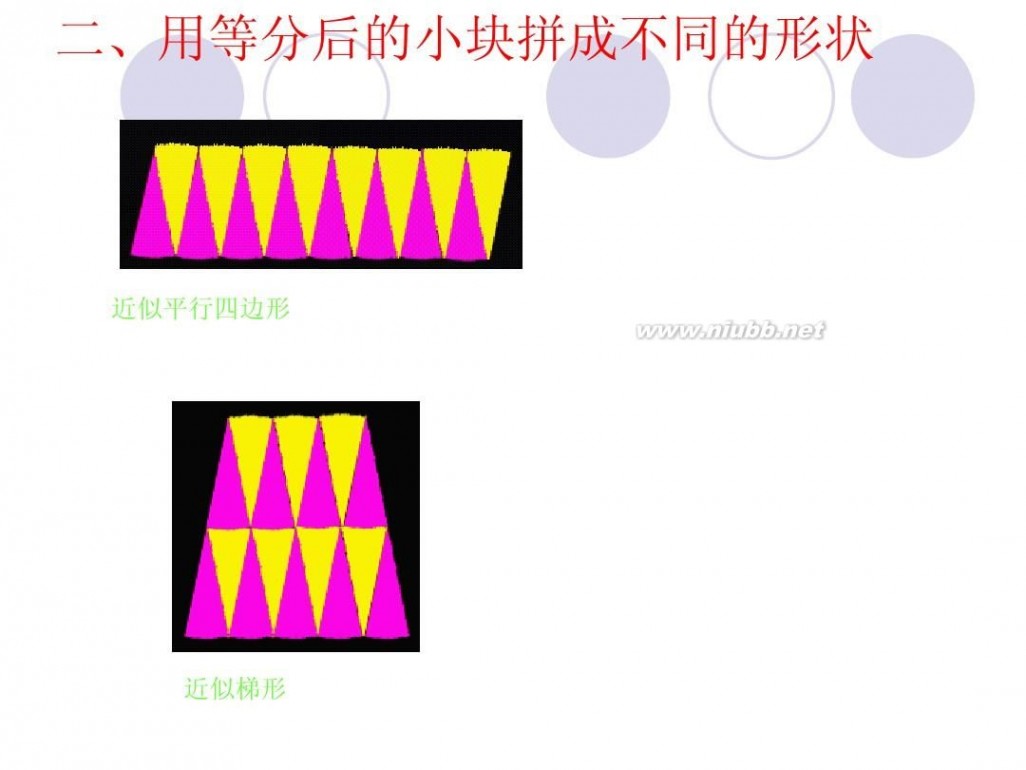
圆面积的推导过程 圆的面积公式推导
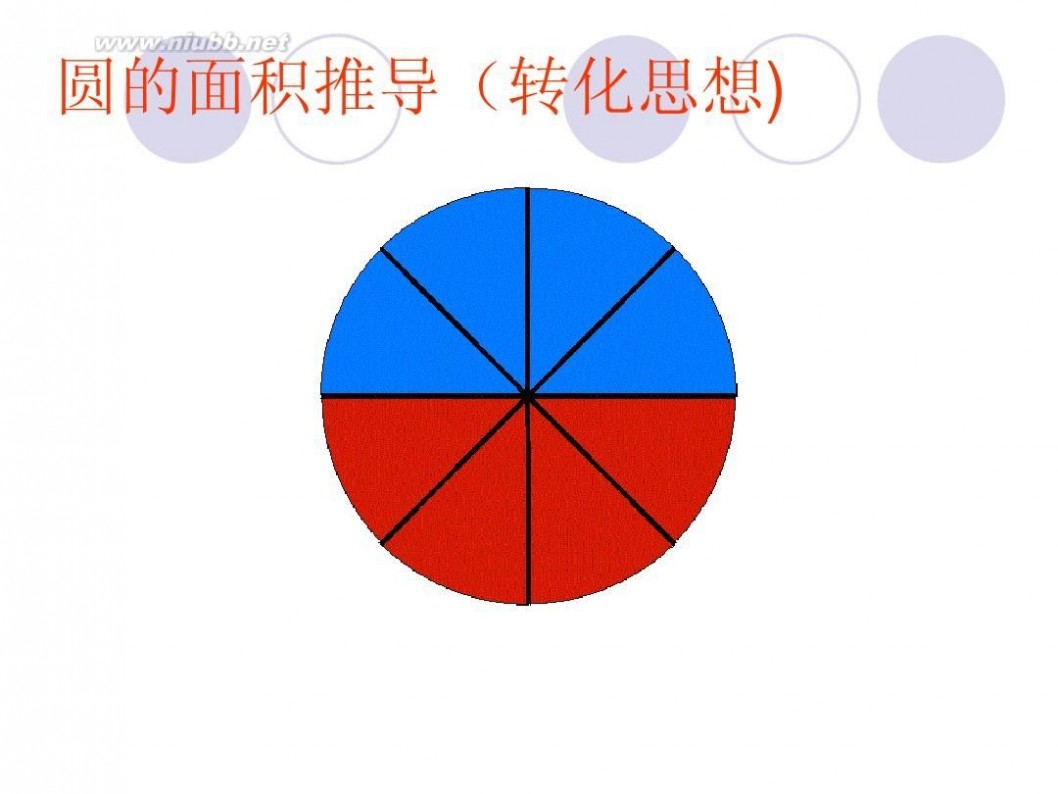
圆面积的推导过程 圆的面积公式推导
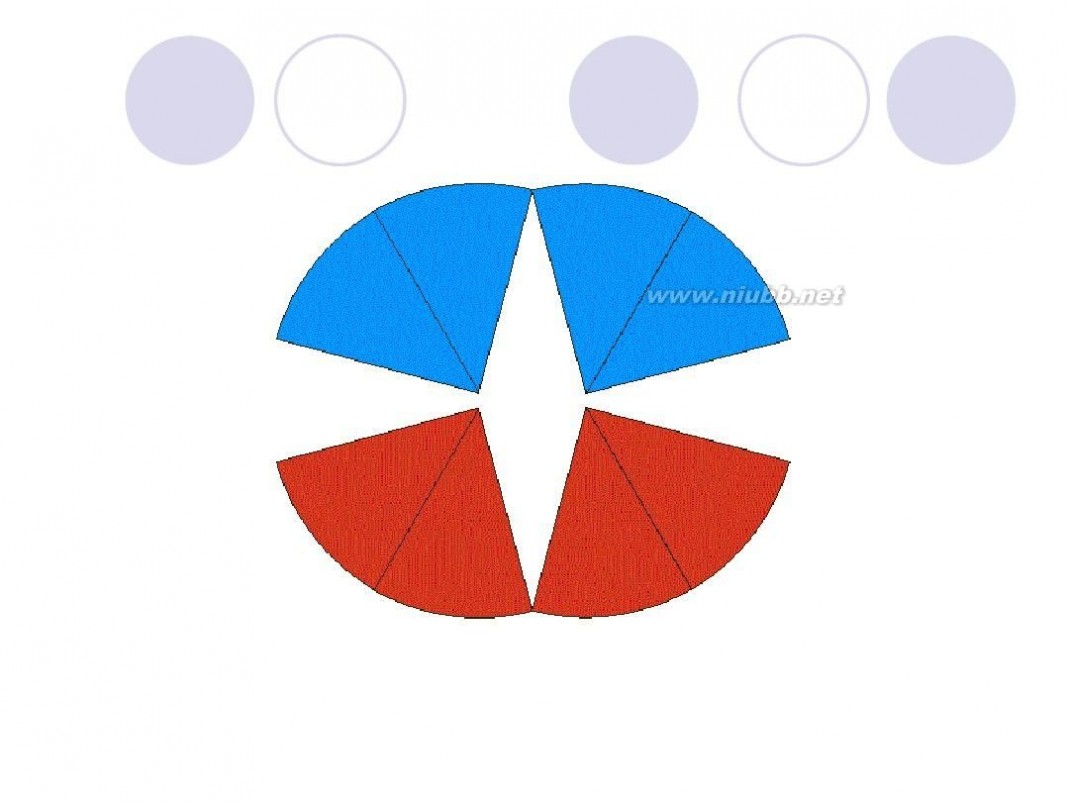
圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导
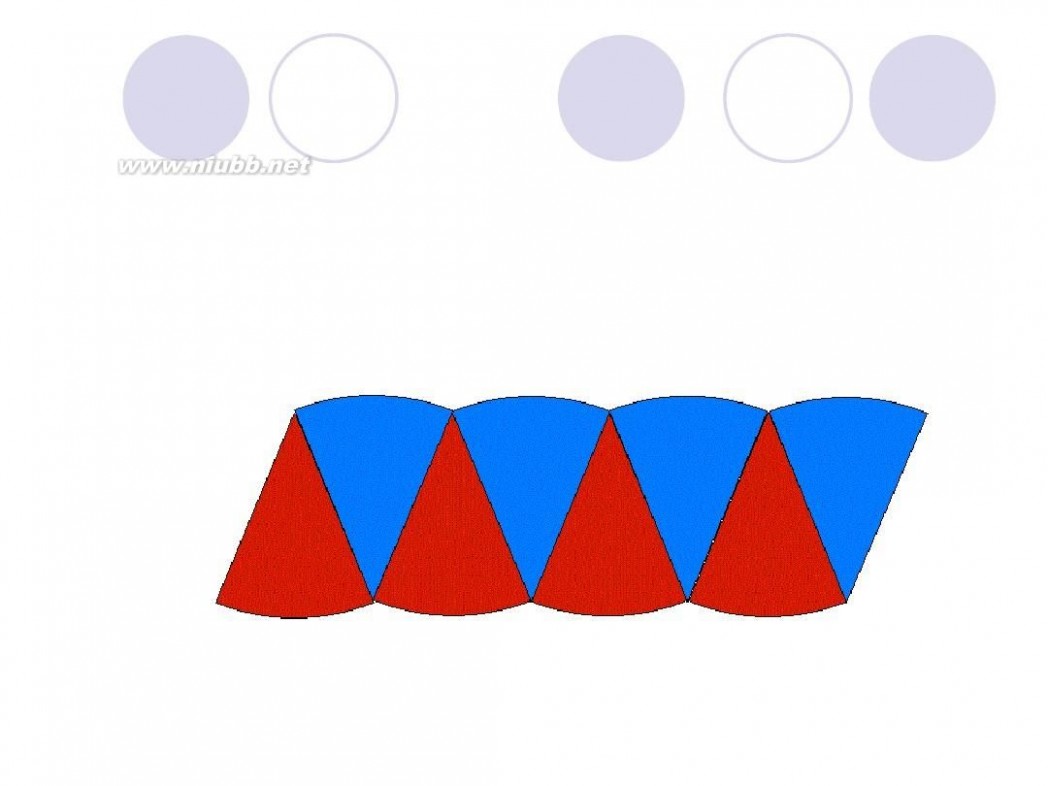
圆面积的推导过程 圆的面积公式推导
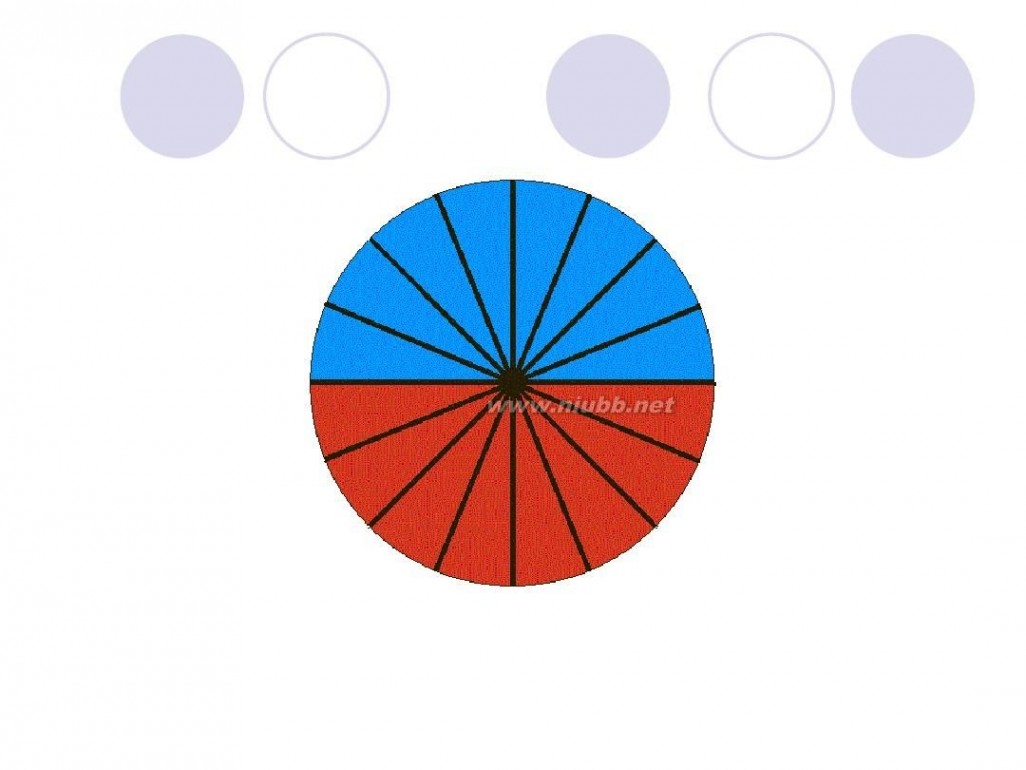
圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导
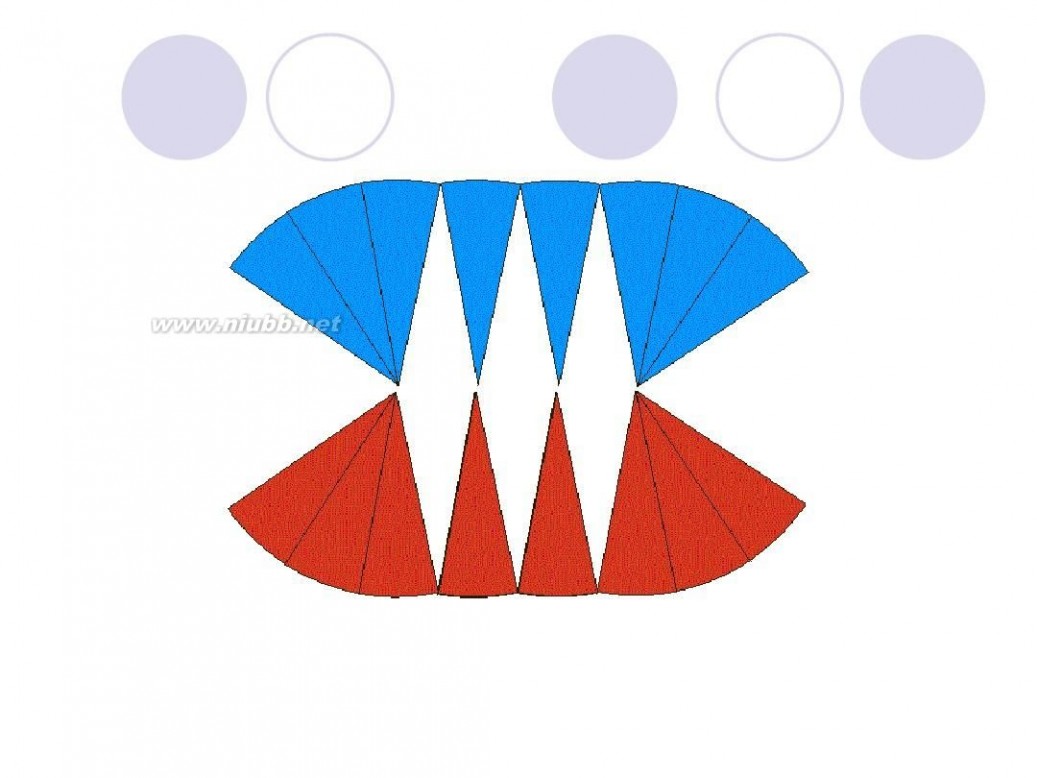
圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导
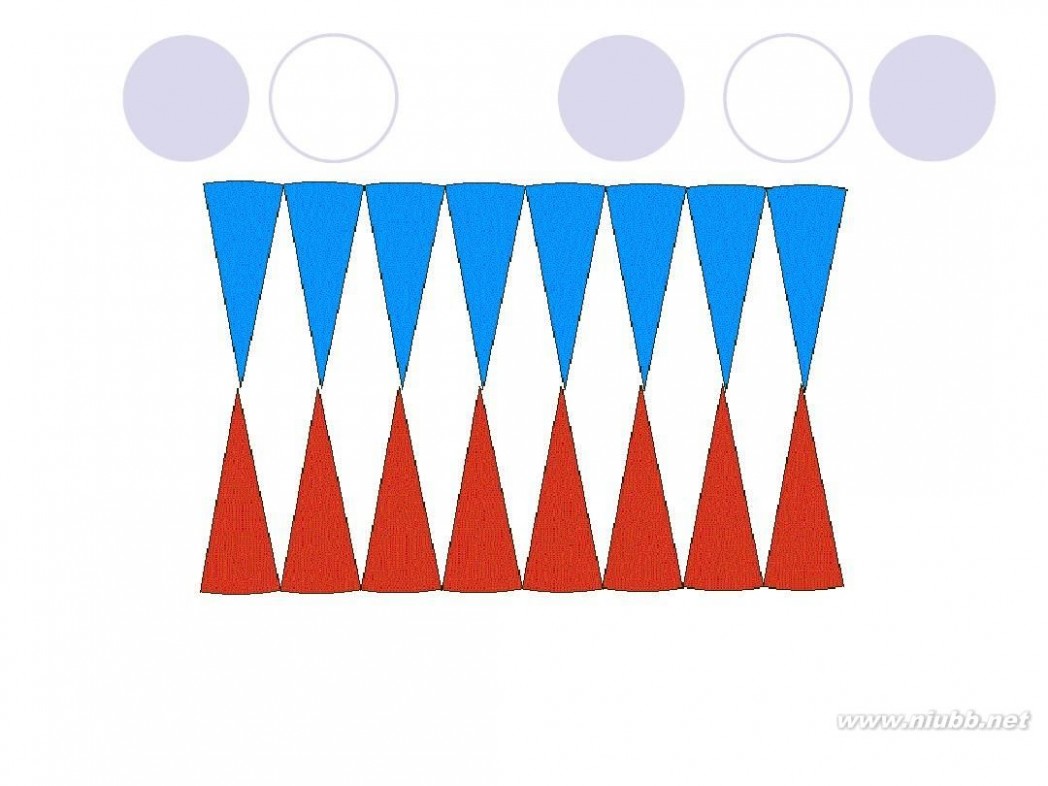
圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导
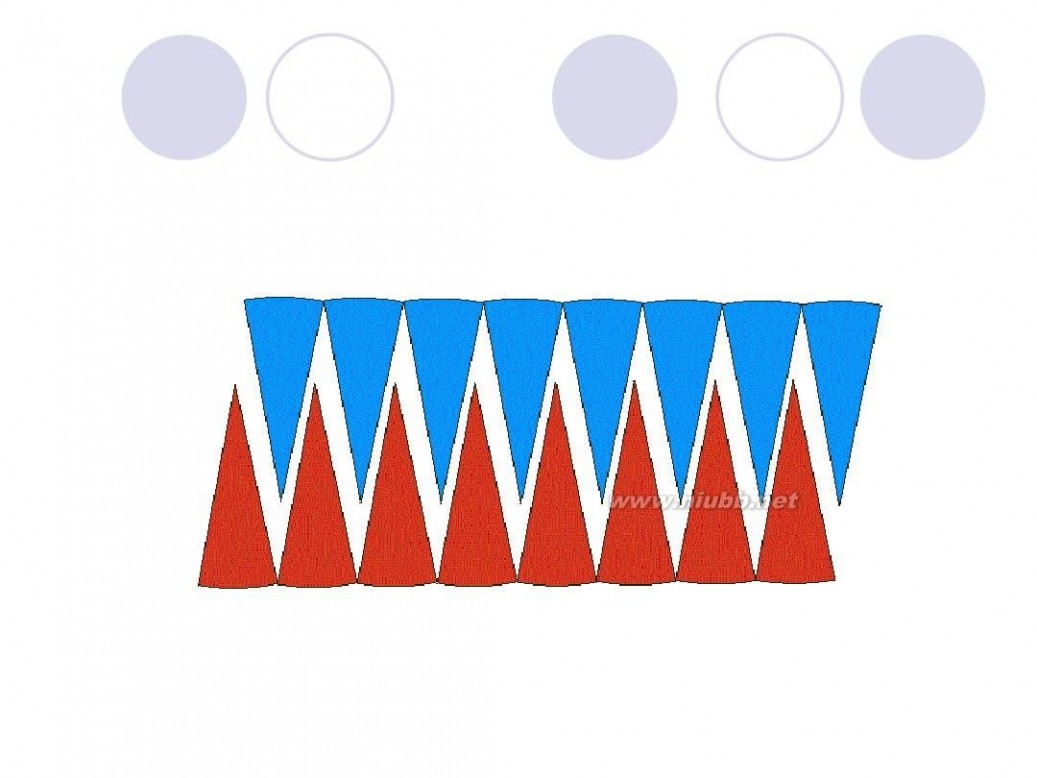
圆面积的推导过程 圆的面积公式推导
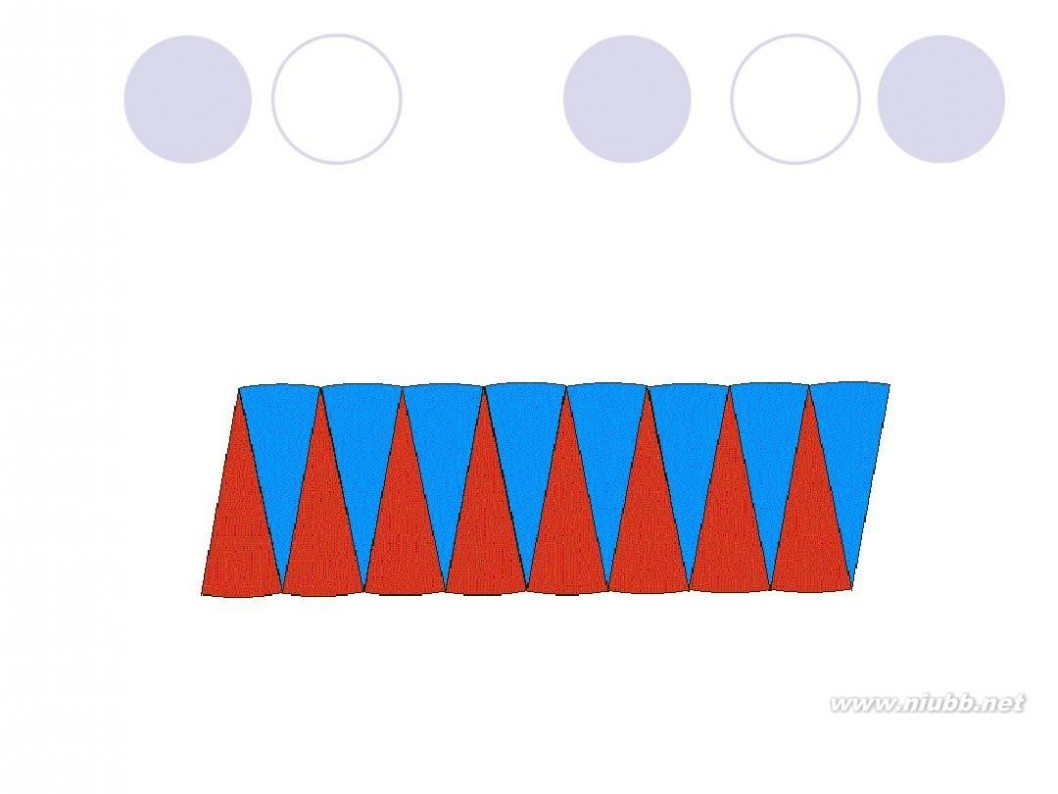
圆面积的推导过程 圆的面积公式推导
圆面积的推导过程 圆的面积公式推导
圆面积的推导过程 圆的面积公式推导
圆面积的推导过程 圆的面积公式推导
圆面积的推导过程 圆的面积公式推导
圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导
圆面积的推导过程 圆的面积公式推导
圆面积的推导过程 圆的面积公式推导
圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导
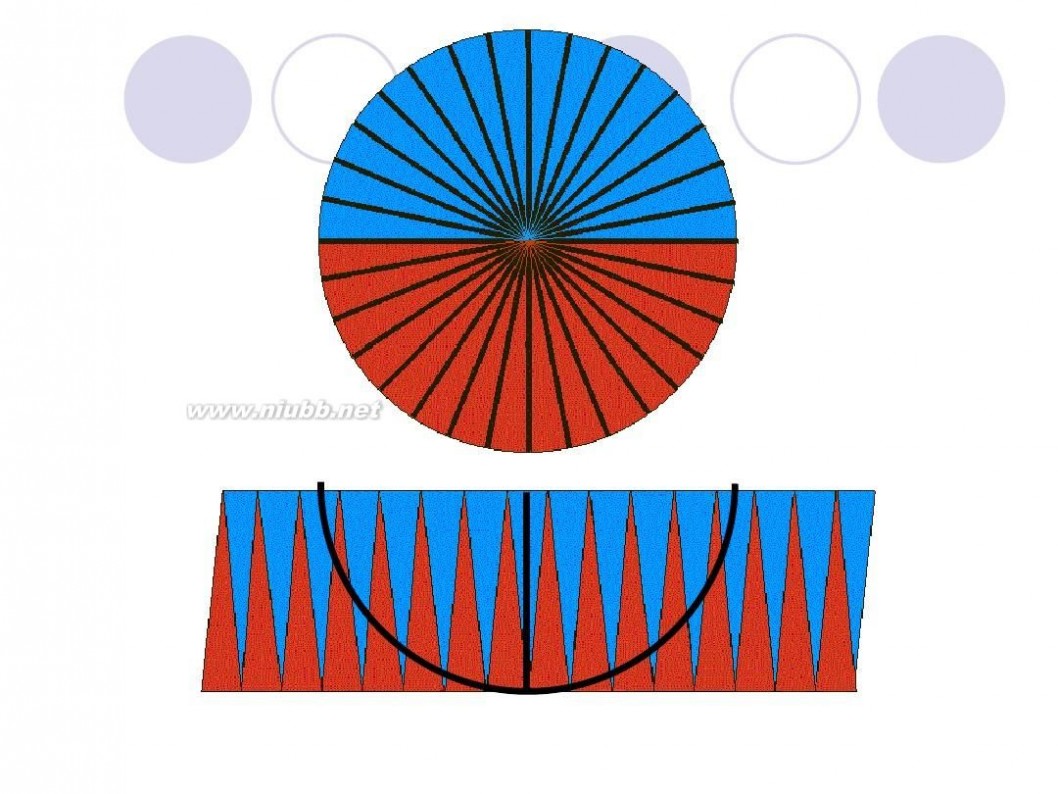
圆面积的推导过程 圆的面积公式推导
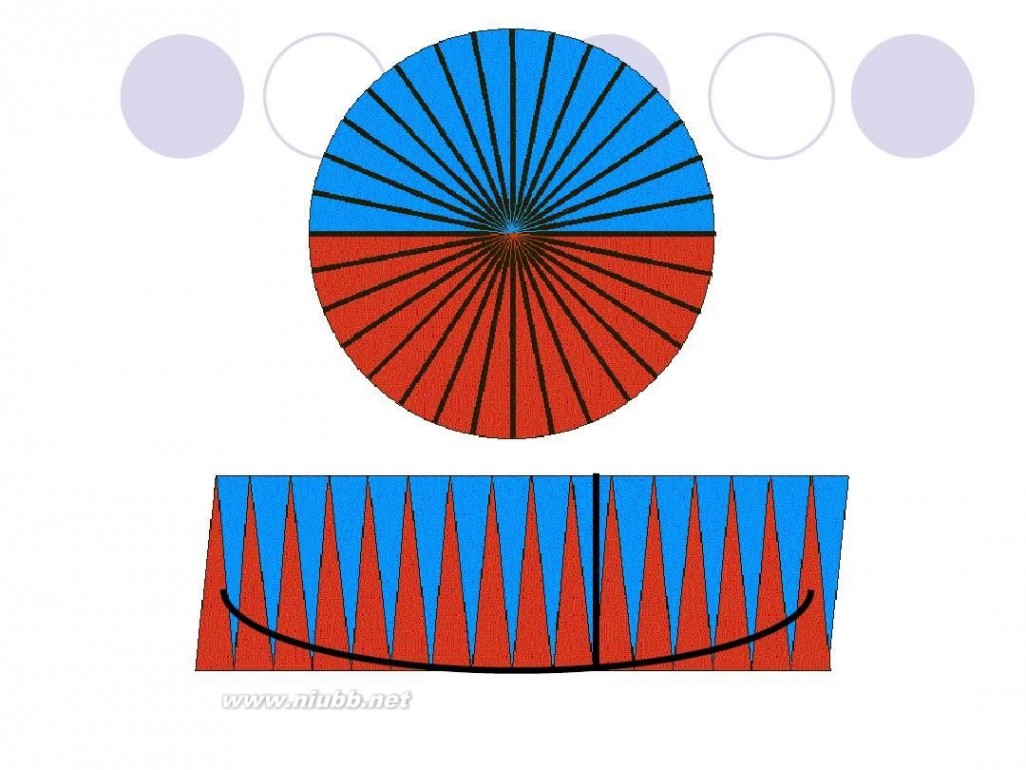
圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导
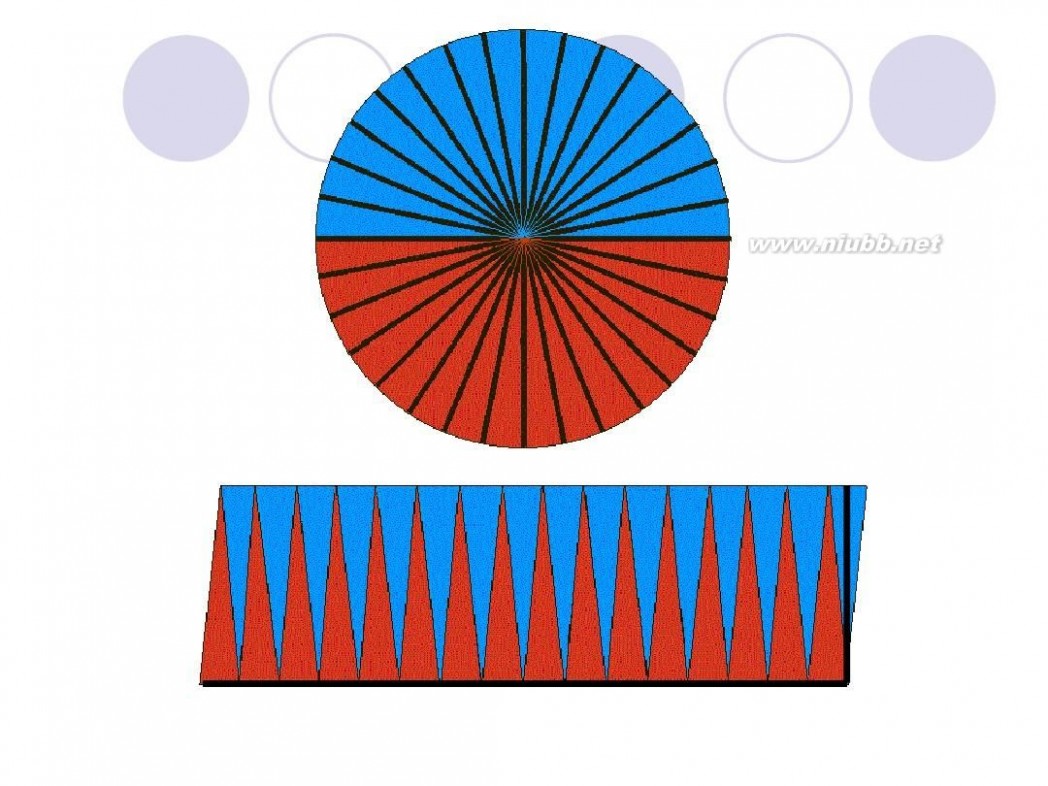
圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导
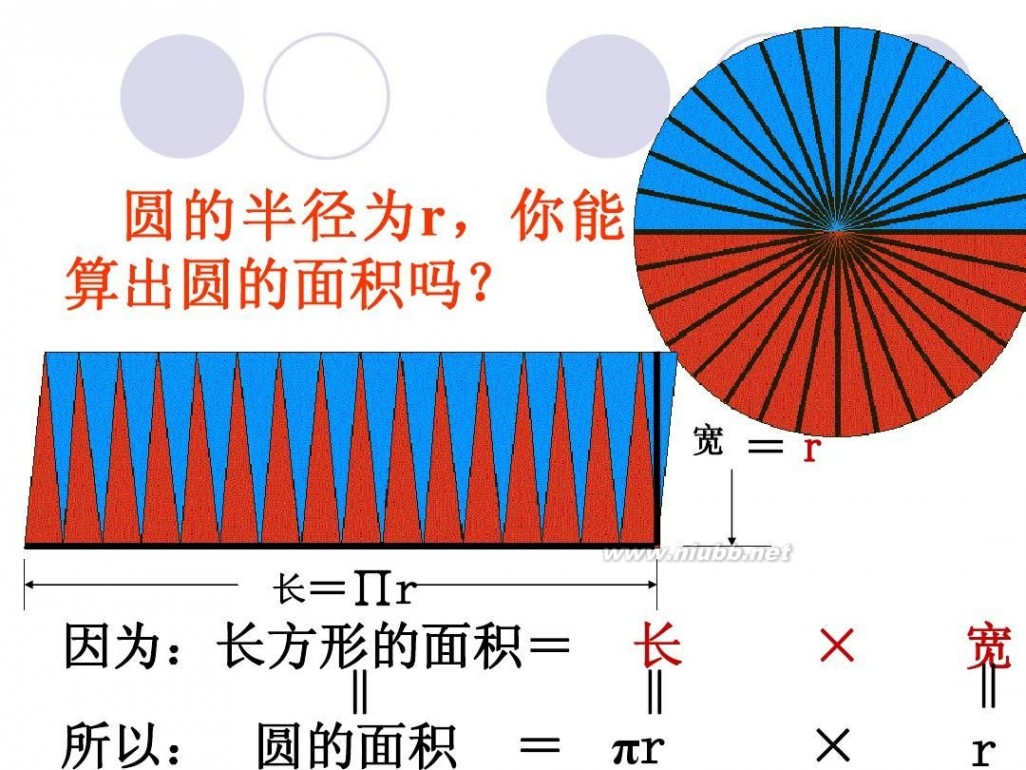
圆面积的推导过程 圆的面积公式推导
圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导
圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导
圆面积的推导过程 圆的面积公式推导

圆面积的推导过程 圆的面积公式推导

61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1