一 : 假设乒乓球团体比赛的规则如下：进行5场比赛，除第3场为双打外，其余各场为单打，参赛的每个队选出3名运

假设乒乓球团体比赛的规则如下：进行5场比赛，除第3场为双打外，其余各场为单打，参赛的每个队选出3名运动员参加比赛，每个队员打两场，且第1、2场与第4、5场不能是某个运动员连续比赛．某队有4名乒乓球运动员，其中A不适合双打，则该队教练安排运动员参加比赛的方法共有（　　）种． A．48 B．56 C．60 D．72

题型：单选题难度：偏易来源：不详

将4名运动员分别记为A、B、C、D： 分两种情况考虑，第一种是4选3时没有选到A，第二种是4选3时选到了A 1、第一种情况：4选3时没有选到A，则B、C、D参加比赛 第一场单打比赛的安排方法有3种， 第二场单打比赛的安排方法有2种， 第三场双打比赛的安排方法有2种（因为打了一二场的两名选手不能组合打双打，否则第4、5两场就是一人连打了）， 第四场单打比赛的安排方法有2种， 第五场单打比赛的安排方法有1种 共有3×2×2×2×1=24种安排方法． 2、第二种情况：4选3时选到了A，则有ABC、ABD、ACD三种选法，对于每一种选法，都有： 第三场双打比赛的安排方法有1种， A必在1、2场中选一场，有两种选法，再在4、5场中选一场，有两种选法， 当A选择了1、2场后，剩下一场有两种选法，4、5中剩下的一场只有一种选法了． 共有3×2×2×2×1=24种安排方法． 故总的安排方法有24+24=48种． 故选A

考点：

考点名称：排列与组合

排列：

1、排列的概念：从n个不同元素中取出m（m≤n）个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列。
2、全排列：把n个不同元素全部取出的一个排列，叫做这n个元素的一个全排列。
3、排列数的概念：从n个不同元素中取出m（m≤n）个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号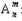表示。
4、阶乘：自然数1到n的连乘积，用n!=1×2×3×…×n表示。
规定：0！＝1
5、排列数公式：=n（n-1）（n-2）（n-3）…（n-m+1）=。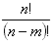

组合：

1、组合的概念：从n个不同元素中取出m个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合。
2、组合数的概念：从n个不同元素中取出m个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数用符号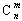表示。
3、组合数公式：；
4、组合数性质：（1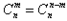）；（2）。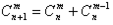
5、排列数与组合数的关系：。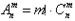

排列与组合的联系与区别：

从排列与组合的定义可以知道，两者都是从n个不同元素中取出m个（m≤n，n，m∈N）元素，这是排列与组合的共同点。它们的不同点是：排列是把取出的元素再按顺序排列成一列，它与元素的顺序有关系，而组合只要把元素取出来就可以，取出的元素与顺序无关．只有元素相同且顺序也相同的两个排列才是相同的排列，否则就不相同；而对于组合，只要两个组合的元素相同，不论元素的顺序如何，都是相同的组合，如a，b与b，a是两个不同的排列，但却是同一个组合。

排列应用题的最基本的解法有：

（1）直接法：以元素为考察对象，先满足特殊元素的要求，再考虑一般元素，称为元素分析法，或以位置为考察对象，先满足特殊位置的要求，再考虑一般位置，称为位置分析法；
（2）间接法：先不考虑附加条件，计算出总排列数，再减去不符合要求的排列数。

排列的定义的理解：

①排列的定义中包含两个基本内容，一是取出元素；二是按照一定的顺序排列；
②只有元素完全相同，并且元素的排列顺序也完全相同时，两个排列才是同一个排列，元素完全相同，但排列顺序不一样或元素不完全相同，排列顺序相同的排列，都不是同一个排列；
③定义中规定了m≤n，如果m<n，称为选排列；如果m=n，称为全排列；
④定义中“一定的顺序”，就是说排列与位置有关，在实际问题中，要由具体问题的性质和条件进行判断，这一点要特别注意；
⑤可以根据排列的定义来判断一个问题是不是排列问题，只有符合排列定义的说法，才是排列问题。

排列的判断：

判断一个问题是否为排列问题的依据是是否与顺序有关，与顺序有关且是从n个不同的元素中任取m个(m≤n)不同元素的问题就是排列问题，否则就不是排列的问题，而检验一个问题是否与顺序有关的依据就是变换不同元素的位置，看其结果是否有变化，若有变化就与顺序有关，就是排列问题；若没有变化，就与顺序无关，就不是排列问题．

写出一个问题中的所有排列的基本方法:

写出一个问题中的所有排列的基本方法是字典排序法或树形图法或框图法。

组合规律总结：

①组合要求n个元素是不同的，被取出的m个元素也是不同的，即从n个不同元素中进行m次不放回的抽取；
②组合取出的m个元素不讲究顺序，也就是说元素没有位置的要求，无序性是组合的本质属性；
③根据组合的定义，只要两个组合中的元素完全相同，那么不论元素的顺序如何，都是相同的组合，而只有两个组合中的元素不完全相同，才是不同的组合．

排列组合应用问题的解题策略：

1.捆绑法：把相邻的若干特殊元素“捆绑”成一个“大元素”，然后再与其余“普通元素”全排列，而后“松绑”，将特殊元素在这些位置上全排列，这就是所谓相邻问题“捆绑法”．
2.插空法：对于不相邻问题用插空法，先排其他没有要求的元素，让不相邻的元素插产生的空．
3.优先排列法：某些元素（或位置）的排法受到限制，列式求解时，应优先考虑这些元素，叫元素分析法，也可优先考虑被优待的位置，叫位置分析法．
4.排除法：这种方法经常用来解决某些元素不在某些位置的问题，先总体考虑，后排除不符合条件的。
5.特殊元素优先考虑，特殊位置优先安排的策略；
6.合理分类和准确分步的策略；
7.排列、组合混合问题先选后排的策略；
8.正难则反，等价转化的策略；
9相邻问题捆绑处理的策略；
10.不相邻问题插空处理的策略；
11.定序问题除法处理的策略；
12.分排问题直接处理的策略；
13.构造模型的策略，

排列的应用：

(1)-般问题的应用：求解排列问题时，正确地理解题意是最关键的一步，要善于把题目中的文字语言翻译成排列的相关术语；正确运用分类加法计数原理和分步乘法计数原理也是十分重要的；还要注意分类时不重不漏，分步时只有依次做完各个步骤，事情才算完成，解决排列应用题的基本思想是：

解简单的排列应用问题，首先必须认真分析题意，看能否把问题归结为排列问题，即是否有顺序，如果是，再进一步分析n个不同的元素是指什么以及从n个不同的元素中任取m个元素的每一种排列对应着什么事情，最后再运用排列数公式求解．
(2)有限制条件的排列问题：在解有限制条件的排列应用题时，要从分析人手，先分析限制条件有哪些，哪些是特殊元素，哪些是特殊位置，识别是哪种基本类型，在限制条件较多时，要抓住关键条件（主要矛盾），通过正确地分类、分步，把复杂问题转化为基本问题，解有限制条件的排列问题的常用方法是：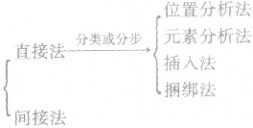

常见类型有：①在与不在：在的先排、不在的可以排在别的位置，也可以采用间接相减法；②邻与不邻：邻的用”，不邻的用”；③间隔排列：有要求的后排（插空）．

组合应用题：

解决组合应用题的基本思想是“化归”，即由实际问题建立组合模型，再由组合数公式来计算其结果，从而得出实际问题的解．
（1）建立组合模型的第一步是分析该实际问题有无顺序，有顺序便不是组合问题．
（2）解组合应用题的基本方法仍然是“直接法”和“间接法”．
（3）在具体计算组合数时，要注意灵活选择组合数的两个公式以及性质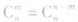的运用．

排列、组合的综合问题：

(1)应遵循的原则：先分类后分步；先选后排；先组合后排列，有限制条件的优先；限制条件多的优先；避免重复和遗漏．
(2)具体途径：在解决一个实际问题的过程中，常常遇到排列、组合的综合性问题．而解决问题的关键是审题，只有认真审题，才能把握问题的实质，分清是排列问题，还是组合问题，还是综合问题，分清分类与分步的标准和方式，并且要遵循两个原则：①按元素的性质进行分类；②按事情发生的过程进行分析．
(3)解排列、组合的综合问题时要注意以下几点：
①分清分类计数原理与分步计数原理：主要看是，还是分步完成；
②分清排列问题与组合问题：主要看是否与序；
③分清是否有限制条件：被限制的元素称为特殊元素，被限制的位置称为特殊位置。
解这类问题通常从以下三种途径考虑：
a．以元素为主考虑，即先满足特殊元素的要求，再考虑其他元素；
b．以位置为主考虑，即先满足特殊位置的要求，再考虑其他位置；
c．先不考虑限制条件，计算出排列或组合数，再减去不合要求的排列或组合数．
前两种叫直接解法，后一种叫间接解法，不论哪种，都应“特殊元素（位置）优先考虑”．
④要特别注意既不要重复，也不要遗漏．

(4)排列、组合应用问题的解题策略：①特殊元素优先考虑，特殊位置优先安排的策略；②合理分类和准确分步的策略；③排列、组合混合问题先选后排的策略；④正难则反，等价转化的策略；⑤相邻问题捆绑处理的策略；⑥不相邻问题插空处理的策略；⑦定序问题除法处理的策略；⑧分排问题直接处理的策略；⑨；⑩构造模型的策略，

二 : 乒乓球男女混双的规则

乒乓球男女混双的规则

---

乒乓球规则

双击自动滚屏 发布者：公体部 发布时间：2005-5-9 阅读：1449次

计分

乒乓球比赛包括男女单打、男女双打和混合双打。双打比赛以两名运动员为一方，单打比赛以一名运动员为一方。有发球权的一方叫发球方，对方叫接发球方。

1.1一分

除被判重发球的回合，下列情况运动员得一分:

(1)对方运动员未能合法发球；

(2)对方运动员未能合法还击；

(3)运动员在发球或还击后，对方运动员在击球前，球触及了除球网装置以外的任何东西；

(4)对方击球后，该球越过本方端线而没有触及本方台区；

(5)对方阻挡；

(6)对方连击；

(7)对方运动员或他穿戴的任何东两使球台移动；

(8)对方运动员或他穿戴的任何东西触及球网装置；

(9)对方运动员不执拍手触及比赛台面；

(10)双打时，对方运动员击球次序错误；

(11)执行轮换发球法时，接发球运动员或其双打同伴，包括接发球一击，完成了13次合法还击；

1.2一局比赛

在一局比赛中，先得21分的一方为胜方，20平后，先多得2分的一方为胜方。

1.3一场比赛

(1)奥运会乒乓球比赛采用五局三胜制，但双打预选赛采用三局两胜制；

(2)一场比赛应连续进行.但在局与局之间，任何一名运动员都有权要求不超过两分钟的休息时间；

2. 发球

2.1发球、接发球和方位的选择

(1)选择发球，接发球和这一方，那一方的权力应由抽签来决定，中签者可 以 选择先发球或先接发球，或选择先在某一方；

(2)当一方运动员选择了先发球或先接发球，或选择先在某一方后，另一方运 动员应有另一个选择的权力.；

(3)在获得每2分之后，接发球方即成为发球方，依此类推，直至该局比赛结束，或者直至双方比分都达到10分或实行轮换发球法，这时，发球和接发次序仍然不变，但每人只轮发一分球；

4)在双打的第一局比赛中，先发球方确定第一发球员，再由先接发球方确定第一接发球员.在以后的各局比赛中，第一发球员确定后，第一接发球员应是前一局发球给他的运动员；

(5)在双打中，每次换发球时，前面的接发球员应成为发球员，前面的发球员的同伴应成为接发球员；

(6)一局中首先发球的一方，在该场下一局应首先接发球。在双打决胜局中，当一方先得10分时，接发球方应交换接发球次序；

(7)一局中，在某一方位比赛的一方，在该场下一局应换到另一方位。在决胜局中，一方先得10分时，双方应交换方位；

2.2合法发球

(1)发球时，球应放在不执拍的手掌上，手掌张开和伸平。球应是静止的，在发球方的端线之后和比赛合面的水平面之上；

(2)发球员须用手把球几乎垂直地向上抛起，不得使球旋转，并使球在离开不执拍手的手掌之后上升不少于16厘米；

(3)当球从抛起的最高点下降时，发球员方可击球，使球首先触及本方台区，然后越过或绕过球网装置，再触及接发球员的台区。在双打中，球应先后触及发球员和接发球员的右半区；

(4)从抛球前球静止的最后一瞬间到击球时，球和球拍应在比赛台面的水平面之上；

(5)击球时，球应在发球方的端线之后，但不能超过发球员身体(手臂、头或腿除外)离端线最远的部分；

(6)运动员发球时，有责任让裁判员或副裁判员看清他是否按照合法发球的规定发球；

(7)如果裁判员怀疑发球员某个发球动作的正确性，并且他或者副裁判员都不能确信该发球动作不合法，一场比赛中此现象第一次出现时，裁判员可以警告发球员而不予判分；

(8)在同一场比赛中，如果运动员发球动作的正确性再次受到怀疑，不管是否出于同样的原因，不再警告而判失一分；

(9)无论是否第一次或任何时候，只要发球员明显没有按照合法发球的规定发球，他将被判失一分，无需警告；

(10)运动员因身体伤病而不能严格遵守合法发球的某些规定时，可由裁判员做出决定免予执行，但须在赛前向裁判员说明；

3. 其它规则

(1)球触网后落在对方台上，判好球；

(2)球擦在对方台边上，判好球；

三 : 对阵表》《男女乒乓球混双比赛对阵表》

男女羽毛球混双比赛对阵表

于莱菏李蠲

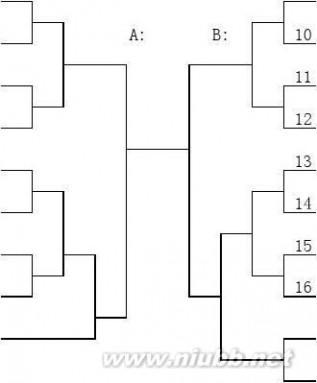
梁东孝张蕾舒一飞黄芬刘勇杨湘洪刘郁王红林李志坚陈畅梁奇峰胡玲霞徐利谋雷英文戈白静该项赛分A,B两组进行单淘汰制取前两名，胜者进总决赛争冠亚军，负者争季军。［www.61k.com］

男女乒乓球混双比赛对阵表王群李亭陈璐肖丽平王丽荣付文亭黄群玲彭莉高艳飞

乒乓球混双 对阵表》《男女乒乓球混双比赛对阵表》

1陈小明

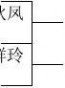
2张立3胡梦湘4邓体俊

5刘庆伦6马跃新7罗红希

8盛传新

9柳孟良

61阅读提醒您本文地址：

本文标题：乒乓球双打比赛规则-假设乒乓球团体比赛的规则如下：进行5场比赛，除第3场为双打外，其余各场为单打，参赛的每个队选出3名运
本文地址： http://www.61k.com/1122896.html