一 : 连续时间信号的卷积42
实验名称 连续时间信号的卷积
一、实验目的:
1、掌握两个连续时间信号卷积的计算方法和编程技术。
2、进一步熟悉用MATLAB描绘二维图像的方法。
二、实验原理:
卷积积分在信号与线性系统分析中具有非常重要的意义,是信号与系统分析的基本方法之一。
(一)卷积的定义
连续时间信号 f1(t)和 f2(t)的卷积积分(简称为卷积)f(t)定义为:
f(t)?f1(t)*f2(t)??f1(?)f2(t??)d? ???
(二)线性时不变(LTI)系统的单位冲激响应
给定一个连续时间LTI系统,在系统的初始条件为零时,用单位冲激信号?(t)作用于系统,此时系统的响应信号称为系统的单位冲激响应(Unit impulse response),一般用h(t)来表示。需要强调的是,系统的单位冲激响应是在激励信号为? (t)时的零状态响应(Zero-state response)。
系统的单位冲激响应是一个非常重要的概念,如果已知一个系统的单位冲激响应,那么,该系统对任意输入信号的响应信号都可以求得。
(三)卷积的意义
对于LTI系统,根据系统的线性和时不变性以及信号可以分解成单位冲激函数可得,任意LTI系统可以完全由它的单位冲激响应h(t)来确定,系统的输入信号x(t)和输出信号y(t)之间的关系可以用卷积运算来描述,即:
y(t)??x(?)h(t??)d? ???
由于系统的单位冲激响应是零状态响应,故按照上式求得的系统响应也是零状态响应。它是描述连续时间系统输入输出关系的一个重要表达式。
(四)函数说明
利用MATLAB的内部函数conv( )可以很容易地完成两个信号的卷积积分运算。其语法为:y = conv(x,h)。其中x和h分别是两个参与卷积运算的信号,y为卷积结果。
为了正确地运用这个函数计算卷积,这里对conv(x,h)做一个详细说明。conv(x,h)函数实际上是完成两个多项式的乘法运算。例如,两个多项式p1和p2分别为:p1?s3?2s2?3s?4 和 p2?4s3?3s2?2s?1
这两个多项式在MATLAB中是用它们的系数构成一个行向量来表示的,用x来表示多项式p1,h表示多项式p2,则x和h分别为
x = [1 2 3 4]
h = [4 3 2 1]
在MATLAB命令窗口依次键入
>> x = [1 2 3 4];
>> h = [4 3 2 1];
>> y=conv(x,h)
在屏幕上得到显示结果:
y = 4 11 20 30 20 11 4
这表明,多项式p1和p2的乘积为:
p3?4s6?11s5?20s4?30s3?20s2?11s?4
用MATLAB处理连续时间信号时,时间变量t的变化步长应该很小,假定用符号dt表示时间变化步长,那么,用函数conv( )作两个信号的卷积积分时,应该在这个函数之前乘以时间步长方能得到正确的结果。也就是说,正确的语句形式应为:y = dt*conv(x,h)。
对于定义在不同时间段的两个时限信号x(t),t1 ≤ t ≤ t2,和h(t),t3 ≤ t ≤ t4。 如果用y(t)来表示它们的卷积结果,则y(t)的持续时间范围应为t0+t2 ≤ t ≤ t1+t3,这个结论很重要。在处理卷积结果的时间范围时,要利用这个结论,将结果的函数值与时间轴的位置和长度关系保持一致。
另,用函数conv( )计算得到的卷积结果的长度为参与卷积的两函数长度之和减1。
可参考以下程序得到卷积结果的时间变量:
%计算卷积结果的非零样值的起点位置,
%k1,k2分别为参与卷积的两函数的时间向量
k0=k1(1)+k2(1);
%计算卷积结果的非零样值的宽度
k3=length(f);
%确定卷积结果的非零样值的时间向量
k=k0:p:k0+(k3-1)*p;
有时候,参与卷积运算的两个函数,可能有一个或者两个都很长,甚至是无限长,MATLAB处理这样的函数时,总是把它看作是一个有限长序列,具体长度由编程者确定。实际上,在信号与系统分析中所遇到的无限函数,通常都是满足绝对可积条件的信号,因此,对信号采取这种截断处理尽管存在误差,但是通过选择合理的信号长度,能够将误差减小到可以接受的程度。
三、实验内容:
1、已知两连续时间信号如下图所示,绘制信号f1(t)、f2(t)及卷积结果f(t)的波形;设时间变化步长dt分别取为0.5、0.1、0.01,当dt取多少时,程序的计算结果就是连续时间卷积的较好近似?
程序为:
t1=0:0.5:2
t2=-1:0.5:1
y1=0.5.*t1.*[ut(t1)-ut(t1-2)]
y2=0.5.*(t2+1).*[ut(t2+1)-ut(t2-1)]
y=0.5.*conv(y1,y2)
t0=t1(1)+t2(1)
t3=length(y)
t=t0:0.5:t0+(t3-1)*0.5
subplot(221)
plot(t1,y1)
title('y1=f(t)')
xlabel('t')
subplot(222)
plot(t2,y2)
title('y2=f(t)')
xlabel('t')
subplot(223)
plot(t,y)
title('y=f1(t)*f2(t)')
xlabel('t')
%定义阶跃函数,以供调用
function x=ut(t)
x=(t>0)
截图为
2、计算信号f1(t)?e?atu(t)和f2(t)?sintu(t)的卷积f(t), f1(t)、f2(t)的时间范围取为0~5,步长值取为0.1。绘制三个信号的波形。 程序为:
t1=0:0.1:5
y1=exp(-0.5*t1).*ut(t1)
y2=sin(t1).*ut(t1)
y=0.1.*conv(y1,y2)
t0=2.*t1(1)
t2=length(y)
t=t0:0.1:t0+(t2-1).*0.1
subplot(131)
plot(t1,y1)
title('y=f1(t)')
subplot(132)
plot(t1,y2)
title('y=f2(t)')
subplot(133)
plot(t,y)
title('y=f1(t)*y2(t)')
%定义阶跃函数,以供调用 function x=ut(t) x=(t>0)
截图为:
二 : 《信号与系统》中卷积积分教学探讨
摘要:卷积积分是信号与系统中用来求解系统零状态响应的重要工具。通过一道题目使用不同的方法求解:根据卷积的定义求、根据卷积的延时性质求、根据卷积的微积分性质求,最后用MATLAB语言编程验证,表明四种方法求出的结果是一致的。在教学中,鼓励学生一题多解,灵活选用方法,注意各种方法的使用注意点及适用范围,做到举一反三。
关键词:卷积积分;定义法;延时性质法;微积分性质法;MATLAB
中图分类号:G642.4 文献标志码:A 文章编号:1674-9324(2013)51-0058-02
在电子信息类专业《信号与系统》、《数字信号处理》等课程中,卷积积分的概念和计算非常重要。卷积积分是一种重要的数学方法[1],在线性时不变系统中卷积可以用来求取系统的零状态响应。在教学过程中,学生反映卷积概念抽象,计算烦琐。面对高职高专类学生数学基础课课时减少,推导运算能力较薄弱的现状及理论够用的原则,在课堂教学中淡化数学推导,主要讲清卷积的物理意义、作用等,关键是如何应用卷积的定义、性质等计算出卷积结果。卷积积分的计算有多种方法,如根据卷积的定义求、根据卷积的性质(延时性质、微、积分性质)求、图解法、算子计算法[2]、用变换域法求解等。
下面通过教材[3]上一个练习题来探讨卷积积分的求法。
一、例题求解
信号f1(t)和f2(t)的波形如图1所示,试求卷积积分y(t)=f1(t)*f2(t),画出y(t)的波形,并用MATLAB验证之。
(一)根据卷积的定义求
卷积的定义为:设有定义在(-∞,∞)区间上的两个函数f1(t)和f2(t),则其卷积为:
y(t)=f1(t)*f2(t)=■f1(τ)f2(t-τ)dτ
分析求解:使用定义求卷积,需先将f1(t)和f2(t)的解析式写出来。通常我们借助阶跃函数ε(t)和ε(t-t0)延时阶跃函数 来表示信号的闭式解析式,主要是确定非零函数值的区间。
f1(t)=ε(t)-ε(t-2) f2(t)=2[ε(t)-ε(t-1)]
根据卷积的定义知
y(t)=f1(t)*f2(t)=■f1(τ)f2(t-τ)dτ=■[ε(τ)-ε(τ-2)]g2[ε(t-τ)-ε(t-τ-1)]dτ
学生在计算到了这一步犯了难,不知如何往下计算。
这里的关键是要简化被积函数和确定积分的上、下限,紧紧抓住单位阶跃函数ε(t)的定义,在自变量t>0时,取值为1,其他都为0。
综合知:当0≤τ≤2时ε(τ)-ε(τ-2)=1;当t-1≤τ≤t时,ε(t-τ)-ε(t-τ-1)=1,即当0≤τ≤2且t-1≤τ≤t时,被积函数为2。为确定积分上、下限,需要分情况讨论t的范围。
思考过程:0≤τ≤2的范围是固定的,确定在τ轴上,而t-1≤τ≤t的范围随着t的变化在τ轴上移动,但是其长度保持为1不变。可以找出t的5种情况,其对应的积分上、下限和卷积积分结果分别为:
(1)t<0,y(t)=0;(2)0≤t<1,y(t)=■2dτ=2t
(3)1≤t<2,y(t)=■2dτ=2;(4)2≤t<3,y(t)=■2dτ=2-(t-1)=3-t
(5)t>3,y(t)=0
画出y(t)的图形为图2(d)所示。
说明:这道题目若利用卷积的定义求解,在确定积分上、下限和被积函数时比较烦琐。若在写出两个信号的解析式后借助卷积的性质求解会简单些。
(二)根据卷积的延时性质求
卷积的延时性质为:若y(t)=f1(t)*f2(t),有
f1(t-t1)ε(t-t1)*f2(t-t2)ε(t-t2)=y(t-t1-t2)ε(t-t1-t2)
分析求解:y(t)=f1(t)*f2(t)=[ε(t)-ε(t-2)]*[ε(t)-ε(t-1)]=ε(t)*2ε(t)-ε(t)*2ε(t-1)-ε(t-2)*2ε(t)+ε(t-2)*2ε(t-1),
已知ε(t)*ε(t)=tε(t),根据延时性质有
y(t)=2tε(t)-2(t-1)ε(t-1)-2(t-2)ε(t-2)+2(t-3)ε(t-3)
画出波形后与图2(d)相同。
(三)根据卷积的微、积分特性求
卷积的微分特性:若y(t)=f1(t)*f2(t)则:y'1(t)=f1(t)*f'2(t)=f1'(t)*f2(t)
卷积的积分特性:若y(t)=f1(t)*f2(t),则y(-1)(t)=f1(-1)(t)*f2(t)=f1(t)*f2(-1)(t)
分析求解:由卷积的微、积分特性有y(t)=f1(t)*f2(t)=f1(-1)(t)*f2'(t)
f2'(t)由两个冲激信号组成,由任意函数与冲激函数的卷积是任意函数本身及卷积的延时性质知f(t)*δ(t)=f(t)
f(t)*δ(t-t0)=f(t-t0)。
所以任意信号与冲激函数或延时的冲激函数相卷积,相当于将信号波形复制、平移、叠加。其过程为:
f1(-1)(t)*f2'(t)=f1(-1)(t)*[2δ(t)-2δ(t-1)]=2f1(-1)(t)-2f1(-1)(t-1)
注意:使用卷积的微积分性质求解,需要满足f1(-∞)=f2(-∞)=0。
(四)利用MATLAB语言编程求
使用MATLAB语言编程运行结果与上述三种方法求出的结果一致。
此题还可以利用图解法或算子计算法求解,此处不再赘述。
二、结论
通过一道求解卷积的练习题,使用三种方法:根据定义求解、根据卷积的延时性质和微积分性质求解,并利用MATLAB语言编程验证。表明:定义求解需要确定积分的上下限和化简被积函数;根据延时性质求解需要知道最基本的信号卷积的结果;根据微、积分性质求解,适用于其中有一个信号是阶跃信号或斜变信号,通过求导后会出现(www.61k.com]冲激信号,并且另外一个信号的积分比较容易得出的情况。在教学中尽力开拓学生的思路,让其选择自己擅长的方法求解,并能够举一反三。
参考文献:
[1]杨林耀.信号与系统[M].北京:中国人民大学出版社,2000.
[2]唐建锋,杨辉罗,湘南.信号与系统中卷积计算方法探讨[J].科技信息,2012,(04):16.
[3]周昌雄.信号与系统[M].西安:西安电子科技大学出版社,2008.
基金项目:2011年江苏省教育教学改革重点课题《依托省工程中心的太阳能光伏发电高技能人才培养模式的研究与实践》(课题编号:2011JSJG091)
作者简介:陈光红(1979-),女,江苏海安人,讲师,工程师,硕士,研究方向:信号与系统、电子技术的教学与研究。
三 : 信号系统 卷积积分

卷积积分 信号系统 卷积积分

卷积积分 信号系统 卷积积分

卷积积分 信号系统 卷积积分

卷积积分 信号系统 卷积积分

卷积积分 信号系统 卷积积分

卷积积分 信号系统 卷积积分
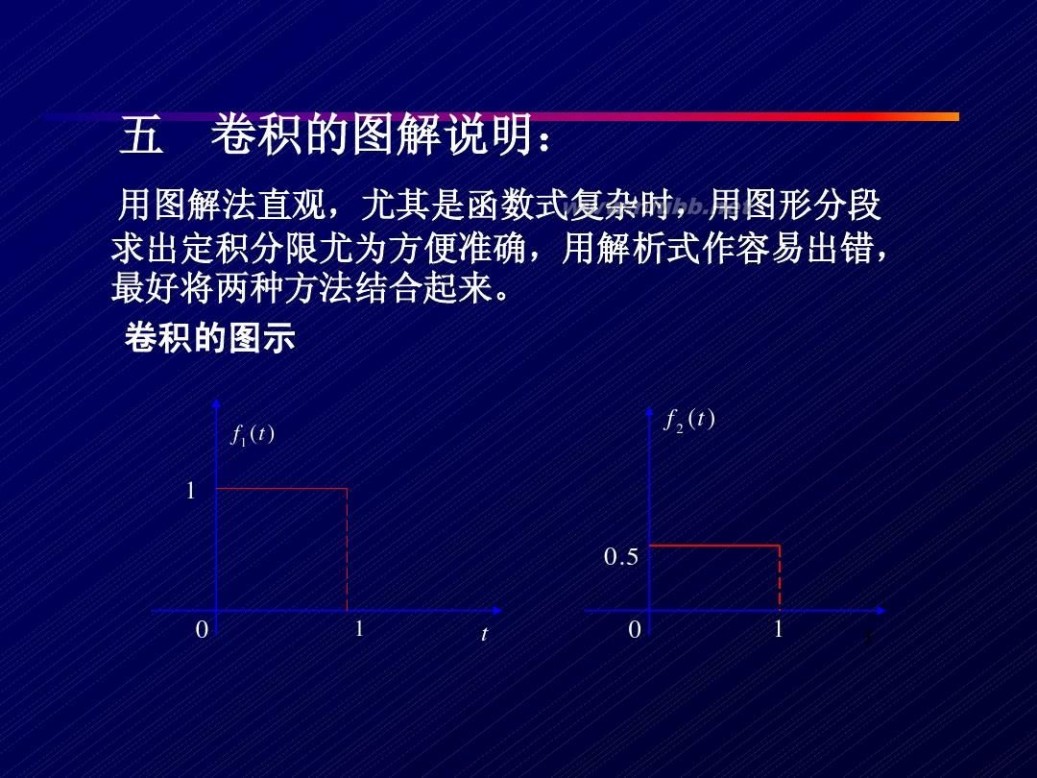
卷积积分 信号系统 卷积积分

卷积积分 信号系统 卷积积分
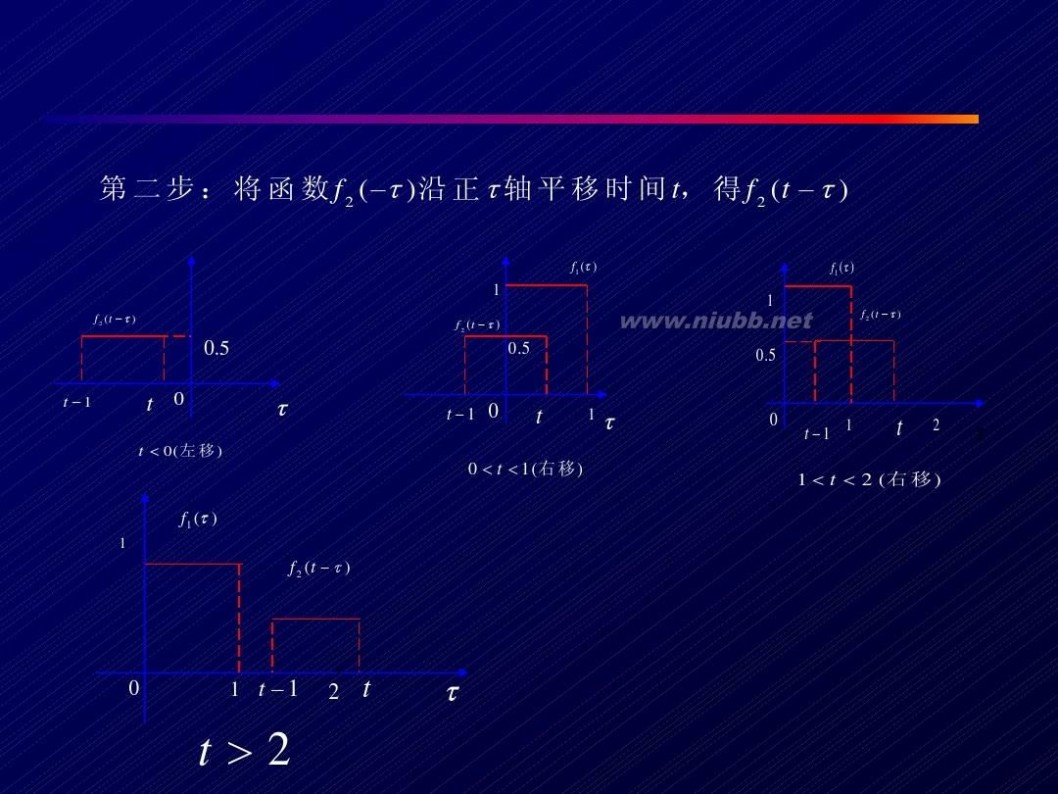
卷积积分 信号系统 卷积积分

卷积积分 信号系统 卷积积分
卷积积分 信号系统 卷积积分
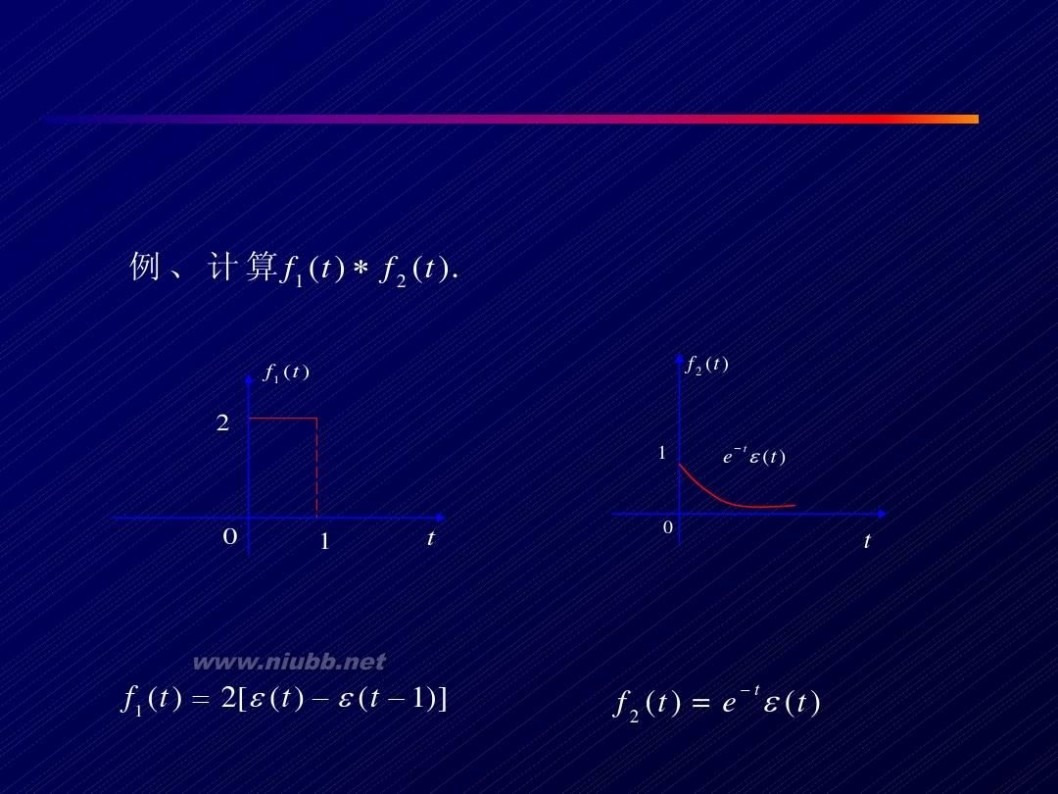
卷积积分 信号系统 卷积积分

卷积积分 信号系统 卷积积分

61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1