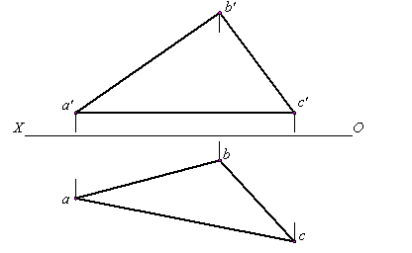
一 : 在三角形ABC内作一直线平行于V面,且距V面20毫米

在三角形ABC内作一直线平行于V面,且距V面20毫米

在三角形ABC内作一直线平行于V面,且距V面20毫米的参考答案

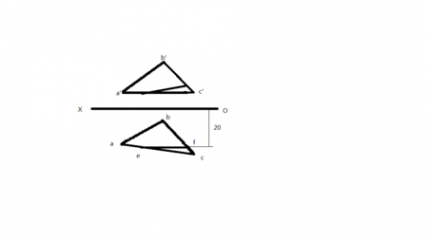
如图做《犇_嫑》线EF//XO轴并使H面的线EF距离X轴20毫米

二 : 在四面体P-ABC中，PA垂直面ABC,三角形ABC为正三角形,?

在四面体P-ABC中，PA垂直面ABC,三角形ABC为正三角形,D,E分别为BC,AC中点,设

AB=2PA=2.
1)如何在B上找一点F,使AD平行面PEF
2)求B到面PEF
3)对于问题1)中F,二面角P-EF-A的大小

---

如图所示：

(1) 设F为DC的中点, 则EF∥AD, EF在面PEF内,AD不在面PEF内, ∴ AD∥面PEF .

(2) 延长FE到H,使FH=AD,△ABC为正三角形,D,BC中点, ∴ AD∥BC, FH∥AD, ∴ FH⊥BC,ADFH是矩形,FH⊥AH, PA⊥面ABC,AH是PH在面ABC的射影, 由三垂线逆定理,FH⊥PH, FH⊥PA, ∴ FH在面PEF内, ∴ 面PAH⊥面PEF, 面PAH∩面PEF=PH,作AG⊥PH,则AG⊥面PEF, 又∵ AD∥面PEF,

∴ AG=D到面PEF的距离=PA×AH/PH=√5/5,则B到面PEF的距离=1+(√5/5)

(3) 由(2)知AH⊥EF,PH⊥EF , ∴ ∠AHP是二面角P-EF-A的平面角,

tan∠AHP=PA/AH=2, ∴ 二面角P-EF-A的大小arctan2

(4) 点B到面PEC的距离更简单:

∵ PA⊥面ABC,PA在面PEC内,∴ 面ABC⊥面PEC,面ABC∩面PEC=EC,而BE⊥EC,∴ BE⊥面ABC⊥面PEC,BE=√3就是点B到面PEC的距离.

本文标题：在直角三角形abc中-在三角形ABC内作一直线平行于V面,且距V面20毫米
本文地址： http://www.61k.com/1092842.html