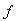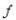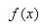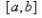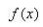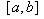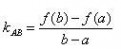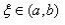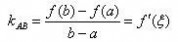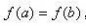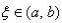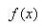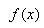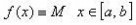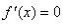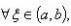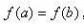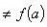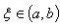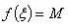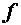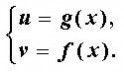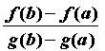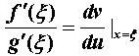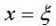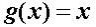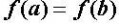一 : 中值定理的应用有哪些

中值定理的应用有哪些

中值定理的应用有哪些的参考答案

零点定理是一个大家平时生活中用惯了以至于反而觉得很陌生的一个定理.若函数f(x)在区间[a,b]连续,并且f(a)与f(b)异号,那在(a,b) 之间一定存在某个x,使得f(x)=0.如果你从海拔为-100的地方走到海拔为400的地方,那不管你是怎么走的,你一定会有经过了海平面的一瞬间.另一个比较隐蔽一些的应用便是,对任意一个凸多边形,总存在一条直线把它分成面积相等的两份.考虑一条竖直直线从左至右扫过整个凸多边形,则凸多边形位于直线左边的那部分面积由0逐渐增大为整个凸多边形的面积,直线右侧的面积则由最初的整个凸多边形面积渐渐变为0.若把直线左侧的面积记为f(x),直线右侧的面积记为g(x),则随着直线位置x的变化,f(x)-g(x)的值由一个负数连续地变为了一个正数,它一定经过了一个零点.这表明,在某一时刻一定有 f(x)=g(x).

二 : 中值定理：中值定理-概述，中值定理-应用

微分中值定理是反映函数与导数之间联系的重要定理，也是微积分学的理论基础，在许多方面它都有重要的作用，在进行一些公式推导与定理证明中都有很多应用。

中值定理_中值定理 -概述

函数与其导数是2个不同的的函数；而导数只是反映函数在一点的局部特征；如果要了解函数在其定义域上的整体性态，就需要在导数及函数间建立起联系，微分中值定理就是这种作用。微分中值定理，包括罗尔定理、拉格朗日定理、柯西定理、泰勒定理。是沟通导数值与函数值之间的桥梁，是利用导数的局部性质推断函数的整体性质的工具。以罗尔定理、拉格朗日中值定理和柯西中值定理组成的一组中值定理是一整个微分学的理论基础。拉格朗日中值定理，建立了函数值与导数值之间的定量联系，因而可用中值定理通过导数去研究函数的性态；中值定理的主要作用在于理论分析和证明；同时由柯西中值定理还可导出1个求极限的洛必达法则。中值定理的应用主要是以中值定理为基础，应用导数判断函数上升，下降，取极值，凹形，凸形和拐点等项的重要性态。从而能把握住函数图象的各种几何特征。在极值问题上也有重要的实际应用。

［www.61k.com]中值定理_中值定理 -应用

（一）对于不等式与等式证明中的应用

在一些等式的证明中，我们往往容易思维定式，只是对于原来的式子要从哪去证明，很不容易去联系其它，只从式子本身所表达的意思去证明。已知有这样1个推论，若函数

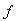
中值定理在区间I上可导，且
中值定理，则
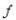
中值定理为I上的1个常量函数。它的几何意义为：斜率处处为0的曲线一定是平行于y轴的直线。这个推论的证明应用拉格朗日中值定理。

（二）关于方程根的讨论（存在性与根的个数）

中值定理

（三）在洛比达法则中证明的应用

无穷小（大）量阶的比较时，看到2个无穷小（大）量之比的极限可能存在，也可能不存在。如果存在，其极限值也不尽相同。称2个无穷小量或2个无穷大量之比的极限为

中值定理型或
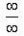
中值定理型不定式极限。解决这种极限的问题通常要用到洛比达法则。这是法则的内容，而在计算时往往都是直接的应用结论，没有注意到定理本身的证明，而这个定理的证明也应用到了中值定理。

（四）定理之间的关系应用

在一元函数微分学中，微分中值定理是应用函数的局部性质研究函数在区间上整体性质的重要工具，它在数学分析中占有重要的地位，其中拉格朗日中值定理是核心，罗尔定理是其特殊情况，柯西定理是起推广。拉格朗日微分中值定理有许多推广，这些推广有一些基本的特点，这就是把定理条件中可微性概念拓宽，然后推广微分中值表达公式。微分中值定理的应用为数学的进1步发展提供了广阔的天地，在以后的学习中还会有其他的应用，再做更为全面的总结。

中值定理_中值定理 -拉格朗日中值定理

拉格朗日，法国数学家、物理学家，19岁时就当上了教授，二十岁为普鲁士科学院院士。他在数学、力学和天文学3个学科领域中都有历史性的贡献。

中值定理
该定理的证明不难，关键是构造1个辅助函数，这里就不作证明了，只给出它的几何说明：
将代数语言 翻译成几何图形语言：
1.
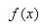
中值定理在
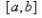
中值定理上连续； ------曲线是连续的、光滑的、不间断的。

2.

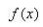
中值定理在
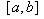
中值定理上可导； ------ 曲线上点点切线都存在（除端点外，处处具有不垂直于X轴的切线）曲线在几何图形上表现为圆弧的，顺的，没有尖点。
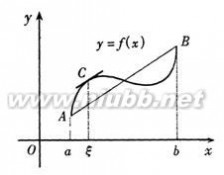
中值定理

满足条件1，2的这样一条曲线过两端点的割线存在，其斜率

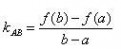
中值定理。割线存在，可以经过平移，可平移到与曲线相切的位置，切点为
中值定理，其中
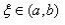
中值定理这样的 点是存在的。

此时切线与原割线平行，斜率相同 ：

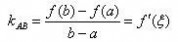
中值定理即结论。
定理中至少存在一点
中值定理， 如果向下平移，图中就有2个这样的点，也有可能3、4、5…个

中值定理_中值定理 -罗尔定理

设

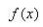
中值定理在闭区间［a，b］ 上连续， 在开区间（a，b）内可导，且
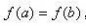
中值定理，则至少存在一点
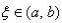
中值定理，使
中值定理

证明：因

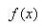
中值定理在［a，b］上连续，据闭区间上连续函数最大值和最小值定理，
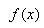
中值定理在［a，b］上必取得最大值M和最小值m，这样有2种可能的情形：

（1） M=m，这时

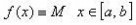
中值定理， 所以
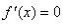
中值定理故：
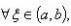
中值定理都有
中值定理，定理成立。

（2） M >m，这时M和m中至少有1个不等于

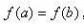
中值定理。不妨设M
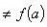
中值定理，则至少存在一点
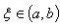
中值定理使
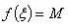
中值定理

中值定理_中值定理 -柯西中值定理

柯西简洁而严格地证明了微积分学基本定理即牛顿－莱布尼茨公式。他利用定积分严格证明了带余项的泰勒公式，还用微分与积分中值定理表示曲边梯形的面积，推导了平面曲线之间图形的面积、曲面面积和立体体积的公式。

中值定理

1.柯西中值定理有着与前2个中值定理相类似的几何意义。只是现在要把

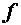
中值定理，
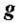
中值定理这2个函数写作以x为参数的参量方程
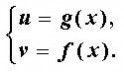
中值定理在uov平面上表示一段曲线（图）。
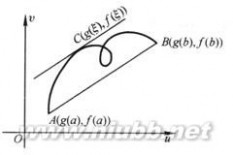
中值定理

由于（1）式右边的

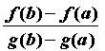
中值定理表示连接该曲线两端的弦AB的斜率，而（1）式左边的
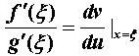
中值定理则表示该曲线上与
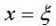
中值定理相对应的一点
中值定理处的切线的斜率。因此（1）式即表示上述切线与弦AB互相平行。

2.a>b时，Cauchy中值定理的结论仍成立。

3.如果取函数

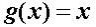
中值定理，Cauchy中值定理就变成Lagrange中值定理了，所以Cauchy中值定理是Lagrange中值定理的推广，Rolle中值定理是Lagrange中值定理的特殊情况（要求
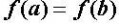
中值定理）；Lagrange中值定理是中值定理的核心定理，故称之为微分学中值定理。

中值定理_中值定理 -参考文献

[1]刘广云：《数学分析选讲》 黑龙江教育出版社2000年
[2]齐民友：《微积分学习指导》 武汉大学出版社 2004年
[3]赵树原：《微积分》 中国人民大学出版社2001年

三 : F与F0值在灭菌中的应用

灭菌法是指杀死或除去所有衍生物的方法。

F值表示在变温条件下t分钟灭菌的效果与在温度T0为时灭菌F分钟的效果是相同的。即F值可把变温条件下的灭菌时间转化在T0时灭菌的等效的时间值。F值常用于干热灭菌。

F0是任意温度湿热灭菌过程以Z=10度，理想灭菌温度（121度）为参比标准的杀菌效果医学教育|网收集整理（以时间为单位）的量值，它包括了灭菌过程中升温、恒温、冷却三个阶段热能对衍生物的总致死效果，所以，它是用时间作单位表示湿热灭菌效果的量值。一般要求F0≥8。

近年来对灭菌过程无菌检验中存在的问题引起人们的注意。一方面灭菌温度多系测量灭菌器内的温度不是灭菌物体内的温度，同时无菌检验方法也在局限性。在检品存在微量的微生物时，往往难以用现行的无菌检验法检出。因此，人们对认识到对灭菌方法的可靠性进行验证是很必要的。F（或F0）值可作用验证灭菌可靠性的参数。

（一）微生物致死间曲线与D值人们对微生物死亡的动力学研究表明，其死亡速度属一级过程。为原始微生物数，Nt为残存的微生物t时残存的微生物。残存数的对数时间作图，得一条直线，直线的斜率＝K／2.303，K为速度常数，单位为时间。为了方便起见，引用D，并定义D为一定温度下杀死被灭菌物品中微生物99％所需时间。

因此，D也可定义为降低微生物一个十位数（）或一个对数值（如log100降低到log10）所需的时间。D值因微生物的种类、环境、灭菌温度不同而各异（表1）。

（二）Z值一旦在不同温度下对特定的微生物的在特定介质或环境中求得D值后，就可用logD值对温度作图，在一定温度范围内，logD与T呈直线关系，直线的斜率＝logD2－logD1／T2－T1。由于此斜率为负值，为避免引入负数，而提出Z值的概念，Z＝T－T1／logD2－logD1，故定义Z值为降低一个logD值需的温度数，如单位为度，也可以认为Z值是降低微生物数90％所需要的温度数。表2是一些药物溶液的Z值

表1不同灭菌法不同微生物的D值

灭菌方法

微生物

温度（℃）

介质或样品

D值（min）

蒸气灭菌

嗜热脂肪芽孢杆菌

105

5％葡萄糖水溶液

87.8

蒸气灭菌

嗜热脂肪芽孢杆菌

121

5％葡萄糖水溶液

2.4

蒸气灭菌

嗜热脂肪芽孢杆菌

121

注射用水

3.0

蒸气灭菌

产芽胞梭状芽孢杆菌

105

5％葡萄糖水溶液

1.3

干热灭菌

枯草芽胞杆菌

135

纸

16.6

红外线灭菌

枯草芽胞杆菌

160

玻璃板

18秒

表2不同溶液以嗜热脂肪芽孢村菌测定Z值

溶液

Z值℃

5％葡萄糖水溶液

10．3

注射用水

8．4

5％葡萄糖乳酸盐林格氏溶液

11．3

PH7磷酸缓冲液

7．6

（三）F值与Fo值

1. F值的数学表达或可表示如下：

F＝DT×（log100－log10－6）（1-1）

△t是测量被灭菌物温度的时间间隔，一般为0.5－1.0或更小，T是每个△t测量被灭菌的温度，To是参比温度。医学教育网搜集整理按此表达式，F为在一定温度（T），给Z值所产生的灭菌效力与参比温度（To）给定Z值所产生的灭菌效果相同时所相当的时间（equivalent time）以分为单位。例如干热灭菌的参比温度用170，消毁大肠杆菌内毒素（endotoxin of E.Coli）的Z值为54℃，则采用250℃干热灭菌消毁上述内毒素的F值为750℃分。

根据式（1-1），若Nt确定为灭菌效果。同时D＝2.303／K，故也可将在一定温度（T）下杀死容器中全部微手物所需的时间称为F值，它等于D值与微生物数降低值的乘积，F值的意义就更明确了。

2.Fo值为一定灭菌温度（T）Z值为121℃，并假设特别耐湿热的微生物指示剂（嗜热脂肪芽胞杆菌）的Z值为10℃，则显然，Fo值为一定灭菌温度（T）Z值为10 ℃所产生的灭菌效果力相同时所相当的时间（分）。也就是说Fo是将各种灭菌温度使微生物的致死力转换为灭菌物品完全暴露于121℃使微生物致死效力。

灭菌过程中，只需记录被来菌物的温度与时间，就可算出Fo，假设如下数据，△t取0.5分。

时间(min)

0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

温度(℃)

100

102

104

106

108

110

115

114

115

并假设4.0min以后，维持115℃30 min不变，则Fo还可以看作P（2）值与微生物的对数降低值的乘积。Fo＝D121×（logNo－logNt）同样，Nt为灭菌后希望达到微生物残存数，一般取10-6如将含有200个嗜热脂肪芽胞杆菌的5％葡萄糖水溶液以121℃热压灭菌时杀死容器中全部微生物所需要的时间。

Fo值的计算对于验证灭菌效果极为有用，当产品以121℃湿热灭菌时，灭菌器内的温度虽能迅速升到121℃，而被菌物品内部则不然，通过由于包装材料性能及其他因素影响而使。升温度各异，而Fo将随着产品温度（T）变化而呈指数的变化。故温度即使很小的差别（如 0.1-1），将对Fo值产生显著的影响。同时要求测定灭菌物品内的实际温度，故用Fo来监测难灭菌效果肯有重要的意义。由于Fo是将不同灭菌温度折算到相当于121℃湿热灭菌时的效力，故Fo值可作为灭菌过程的比较参数。

为了使Fo测定准确，先应选择灵敏度高，重现性好，精密度为0.1的热电偶，并对热电偶进行校验。灭菌时应将热电偶的探针置于被测物的内部，经灭菌器通向柜外的湿度记录仪，有些灭菌记录仪（digistrip recolder）附有Fo计算器，在灭菌过程中和灭菌后，自动显示Fo值。

另外，还应考虑一些其他因素对Fo值的影响，有人对溶液粘度，容器充填量及容器在灭菌器内的数量与排布进行了研究。结果发现对Fo均有影响，而以后者影响最大。故要注意灭菌器内各层、四角、中间位置热分布是否均匀，并进行实际测定，作出合理排布，以便测得Fo值更可靠。

为了确保灭菌效果，还应注意两个问题，根据Fo＝D121×（logNo－logNt），若N越大，即被灭菌物中微生物越多，则灭菌时间越长，故生产过程中应尽量减少微生物的污染，应采取各种措施使每个容器的含菌数控制在10以下（即（log10≤1）。其次计算Fo时，应适当考虑增加安全因素，一般增加5％，如规定Fo为8分，则实际操作应控制Fo12分为好。 本文标题：中值定理的应用-中值定理的应用有哪些
本文地址： http://www.61k.com/1091400.html