一 : 减肥瘦身的计算公式和标准

所有减肥方法均是直接或间接围绕热量为中心,有效指标为减少热量,健康指标为保护基础代谢 ,持续指标为食欲控制中的饱腹感和满足感。(www.61k.com)
其公式为:体质指数(BMI)=体重(千克,kg)/身高的平方(米,m)
BMI指数是Bo dy Mass Index 的缩写,BMI中文是“体质指数”的意思,是以你的身高体重计算出来的。BMI是世界公认的一种评定 肥胖程 度的分级方法,世界卫生组织(WHO)也以BMI来对肥胖或超重进行定义。BMI具体计算方法是以体 重 的千克 数除以身高平方(米为单位)。
理想体重(Kg)=(18.5~23.9)×身高的平方 (单位m)
例如:一个人的身高为 1 .75米,体重为68千克,他的BMI=68/(1.75^2)=22.2(千克/米^2)当BMI指数为18.5~23.9时属 正常。 B MI是与体内脂肪总量密切相关的指标,该指标考虑了体重和身高两个因素。BMI指数简单、实 用、可反映 全身性超重和肥胖。在测量身体因超重而面临心脏病、高血压等风险时,比单纯的以体重来认定,更具准确性。
不过需要 注意的是,并不是每个人都适用BMI指数的。如:
⒈未满 18岁;
⒉是运动员;
⒊正在做 重量训练;
⒋怀孕或哺乳中;
⒌身体虚 弱或久坐不动的老人。
减肥方法网提示:要减肥瘦身需先知道你的体重和身高,先确定你是否超重了,超了多少。建议从三个方面下手:运动,均衡饮食和改变现有的生活方式.
二 : 标准差的概念与计算方法
标准差的概念与计算方法
标准差(Standard Deviation)是一组数值自平均值分散开来的程度的一种测量观念。[www.61k.com)一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
例如,两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ,但第二个集合具有较小的标准差。
标准差可以当作不确定性的一种测量。例如在物理科学中,做重复性测量时,测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值,测量值的标准差占有决定性重要角色:如果测量平均值与预测值相差太远(同时与标准差数值做比较),则认为测量值与预测值互相矛盾。这很容易理解,因为值都落在一定数值范围之外,可以合理推论预测值是否正确。
标准差的简易计算公式
假设有一组数值 x1, ..., xN (皆为实数),其平均值为:
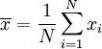
此组数值的标准差为:
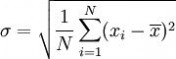
一个较快求解的方式为:
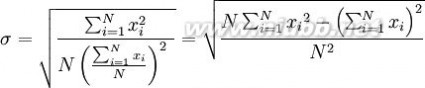
一随机变量X 的标准差定义为:
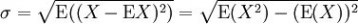
须注意并非所有随机变量都具有标准差,因为有些随机变量不存在期望值。 如果随机变量 X 为 x1,...,xN 具有相同机率,则可用上述公式计算标准差。从一大组数值当中取出一样本数值组合 x1,...,xn ,常定义其样本标准差:
标准差的计算公式 标准差的概念与计算方法
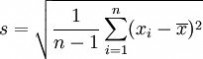
范例
这里示范如何计算一组数的标准差。(www.61k.com)例如一群孩童年龄的数值为 { 5, 6, 8, 9 } : 第一步,计算平均值
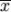

n = 4 (因为集合里有 4 个数),分别设为:
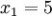
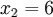
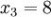
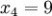

用 4 取代 N

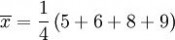
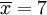
此为平均值。
第二步,计算标准差
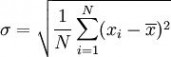

用 4 取代 N
标准差的计算公式 标准差的概念与计算方法
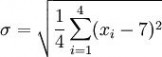
用 7 取代
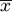
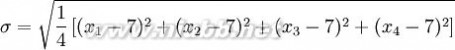
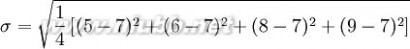
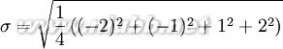
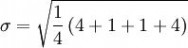
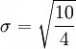
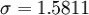
1.2.5试件在规定温度下保湿养生6d,浸水1d后,进行无侧限抗压强度试验,并计算抗压强度试验结果的平均值和偏差系数。(www.61k.com)计算公式为:
R =(R1+R2+R3+......+Rn) (1)
Cv = σ/R (2)
其中:R—混合料所侧强度平均值,MPa;
Ri—各侧定强度值,MPa;
n— 实验样本数;
Cv—偏差系数;
σ—实验结果标准差。[4]
试件的养生规定的温度为:冰冻地区 20±2℃ 非冰冻地区 25±2℃。
1.2.6不同交通类别道路上,水泥稳定混合料的7d浸水抗压强度应符合表-2的规定。
1.2.7根据表-2的强度标准,限定合适的水泥剂量。此剂量试件室内试验结果的平均抗压强度(R`)公式(3)的要求:
R` ≥ Rd /(1- Zа.Cv) (3)
式中:Rd—设计抗压强度;
Cv—试验结果的偏差系数(以小数计);
标准差的计算公式 标准差的概念与计算方法
Zа—标准正态分布表中随保证率而变的系数:高速公路和一级公路应取保证率95%,此时Zа=1.645;一般公路取保证率90%,即Zа=1.282。[www.61k.com]
三 : 标准差的概念与计算方法
标准差的概念与计算方法
标准差(Standard Deviation)是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
例如,两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ,但第二个集合具有较小的标准差。
标准差可以当作不确定性的一种测量。例如在物理科学中,做重复性测量时,测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值,测量值的标准差占有决定性重要角色:如果测量平均值与预测值相差太远(同时与标准差数值做比较),则认为测量值与预测值互相矛盾。这很容易理解,因为值都落在一定数值范围之外,可以合理推论预测值是否正确。
标准差的简易计算公式
假设有一组数值 x1, ..., xN (皆为实数),其平均值为:

此组数值的标准差为:

一个较快求解的方式为:

一随机变量X 的标准差定义为:

须注意并非所有随机变量都具有标准差,因为有些随机变量不存在期望值。 如果随机变量 X 为 x1,...,xN 具有相同机率,则可用上述公式计算标准差。从一大组数值当中取出一样本数值组合 x1,...,xn ,常定义其样本标准差:

范例
这里示范如何计算一组数的标准差。例如一群孩童年龄的数值为 { 5, 6, 8, 9 } : 第一步,计算平均值


n = 4 (因为集合里有 4 个数),分别设为:

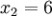

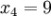
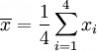
用 4 取代 N

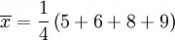

此为平均值。
第二步,计算标准差
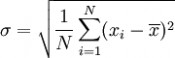

用 4 取代 N

用 7 取代





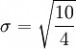
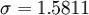
1.2.5试件在规定温度下保湿养生6d,浸水1d后,进行无侧限抗压强度试验,并计算抗压强度试验结果的平均值和偏差系数。计算公式为:
R =(R1+R2+R3+......+Rn) (1)
Cv = σ/R (2)
其中:R—混合料所侧强度平均值,MPa;
Ri—各侧定强度值,MPa;
n— 实验样本数;
Cv—偏差系数;
σ—实验结果标准差。[4]
试件的养生规定的温度为:冰冻地区 20±2℃ 非冰冻地区 25±2℃。
1.2.6不同交通类别道路上,水泥稳定混合料的7d浸水抗压强度应符合表-2的规定。
1.2.7根据表-2的强度标准,限定合适的水泥剂量。此剂量试件室内试验结果的平均抗压强度(R`)公式(3)的要求:
R` ≥ Rd /(1- Zа.Cv) (3)
式中:Rd—设计抗压强度;
Cv—试验结果的偏差系数(以小数计);
Zа—标准正态分布表中随保证率而变的系数:高速公路和一级公路应取保证率95%,此时Zа=1.645;一般公路取保证率90%,即Zа=1.282。
四 : 标准差的概念与计算方法
标准差的概念与计算方法
标准差(Standard Deviation)是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
例如,两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ,但第二个集合具有较小的标准差。
标准差可以当作不确定性的一种测量。例如在物理科学中,做重复性测量时,测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值,测量值的标准差占有决定性重要角色:如果测量平均值与预测值相差太远(同时与标准差数值做比较),则认为测量值与预测值互相矛盾。这很容易理解,因为值都落在一定数值范围之外,可以合理推论预测值是否正确。
标准差的简易计算公式
假设有一组数值 x1, ..., xN (皆为实数),其平均值为:

此组数值的标准差为:

一个较快求解的方式为:

一随机变量X 的标准差定义为:

须注意并非所有随机变量都具有标准差,因为有些随机变量不存在期望值。 如果随机变量 X 为 x1,...,xN 具有相同机率,则可用上述公式计算标准差。从一大组数值当中取出一样本数值组合 x1,...,xn ,常定义其样本标准差:
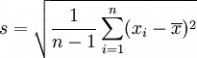
范例
这里示范如何计算一组数的标准差。例如一群孩童年龄的数值为 { 5, 6, 8, 9 } : 第一步,计算平均值


n = 4 (因为集合里有 4 个数),分别设为:
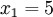


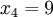

用 4 取代 N


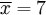
此为平均值。
第二步,计算标准差


用 4 取代 N
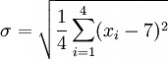
用 7 取代
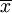

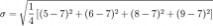




61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1