一 : A present for mother
today is march 28th, my mother’s birthday. today is also sunday. i wanted to make her happy. i gave her a special present. i helped her do some chores and made her have rest all day. i sweep the floor and did the dishes. i also made meal for my mother. that tasted good. my mother was very happy and she told me with tears in her eyes: “ you’re a good kid!” i was very happy too.
1. i sweep the floor and did the dishes. 改为 i swept the floor and did the dishes.
2. i also made meal for my mother改为i also made meals for my mother
3.描述作者母亲生日那天给她的礼物,替母亲干家务,字里行间透出对母亲的爱。
二 : my song for you
故事走到了,这里
该遗忘的事情,都已遁入岁月的深处
我只是不经意的放飞了,手中的那个纸飞机
它便朝着不同的方向飞去
五月的时候,我们曾经站在夕阳下的走廊上
看着纸飞机飞行的航道,划出歪歪扭扭的弧线( 文章阅读网:www.61k.com )
夕阳下,你闪烁着希冀的瞳孔
有些隐隐的哀愁
我亦知晓
许多事,我们都不曾说出口,可是都已经承载在飞机的双翼
飞越千山万水沧海桑田
冷暖自知
在这个冬天即将肆虐来临的时候,我告诉自己
南方的城市,季节早已退去。原来拥有的美丽
四季模糊,服饰无法成为区分温度的标签
长袖短裤,裙子五彩缤纷美丽的如同花朵的颜色
我甚至有点分不清秋夏之间的区别,季节之间的转换,像电影里的镜头
等我们醒悟过来的时候冷风已经过境
潮湿的空气扑面而来。朝南开的那扇窗户关上了就此也再没有人开启过
六月的时候我们有点焦炉不安为了那些即将来到黑暗岁月的人
我看到有人站在走廊里吹起了白色的棉絮
纷纷的棉絮点缀在黑色的天幕下
六月飞雪,我只能用这样毫无创意词语来做比喻
对面的走廊,有人欢呼雀跃
然而置身其中的我们。却只能苦笑着迎接
对于那些无关痛痒的笑颜,早已经成为了那段时间黑白相间的胶片
在我的记忆里它们经不起时间的放映
有时候回想一个人的成长是不是真的循序渐进
为什么我的生命的年轮即将转入第二十圈得时候
还是无法像当初一样,以纯粹和隐忍之心来善待一切
潮水汹涌击打这我的双脚好痛好痛
让人有点不禁皱起眉头
时间也是这样汹涌澎湃
迫不得已的,让我们急需跨过青春的门槛
迈着颠簸的脚步,走向未知的方向
一些人,一些事停留在那个时代透明清澈的宛如你的瞳孔,
时间拉扯着我们一路狂奔
不经意间,我已经走的太远太远
而当我即将离开你的视线时
你会不会站在我的面前还会不会在原地等我?
我不知道自己将走向哪个方向
是沿着朝南的那条铁轨
还是一直延伸
脚印踏在季节的心脏
铿锵的跳动时间狠狠的抽了我一巴掌
可我还是捂着一边脸,然后对他说,麻烦你在扇另一边
如此的自我凌迟
原谅我重视摆出一副阳光灿烂的青春逼人的面孔
总是寻觅借口来排挤忧伤,让自己忙得团团转像一颗疯狂的陀螺
可是只有自己会知道忧伤依然没有停止生长滋生
它们野草般的
塞满了我单薄的肺叶和胸膛
我们说好会一起努力
是吧
那么一切的一切
都变得会有意义
会有意义……
三 : A quantum Monte Carlo algorithm for softcore boson syste
AquantumMonteCarloalgorithmforsoftcorebosonsystems
1,?ˇJurijSmakov,KenjiHarada,2,?andNaokiKawashima3,?
arXiv:cond-mat/0301416v1 [cond-mat.stat-mech] 22 Jan 20032CondensedMatterTheory,DepartmentofPhysics,RoyalInstituteofTechnology,AlbaNovaUniversityCenter,SE-10691Stockholm,SwedenDepartmentofAppliedAnalysisandComplexDynamicalSystems,KyotoUniversity,Kyoto606-8501,Japan3DepartmentofPhysics,TokyoMetropolitanUniversity,Tokyo192-0397,Japan(Dated:February2,2008)Ane?cientQuantumMonteCarloalgorithmforthesimulationofbosonicsystemsonalatticeinagrandcanonicalensembleisproposed.Itisbasedonthemappingofbosonicmodelstothespinmodelsinthelimitofthein?nitetotalspinquantumnumber.Itisdemonstrated,howthislimitmaybetakenexplicitlyinthealgorithm,eliminatingthesystematicerrors.Thee?ciencyofthealgorithmisexaminedforthenon-interactinglatticebosonmodelandcomparedwiththestochasticseriesexpansionmethodwiththeheat-bathtypescatteringprobabilityoftherandomwalker.1Duringthelastfewyearstherewasanincreasingnum-berofreportsonstronglycorrelatedquantumsystems.Alotofattentionhasbeenfocusedonquantumphasetransitions[1]atzerotemperature,whichcanbeob-servedwhenparameterssuchastheparticleconcentra-tionand/ortheinteractionconstantsarevaried.Inordertoobservethequantumphasetransitionexperimentally,onemustbeabletopreciselycontroltheparameter(s),drivingthetransition,whichisusuallyverydi?cultinrealexperimentalsituations.Therefore,onlyanalyti-caltheoriesandnumericalsimulationshavebeenabletoprovideanaccuratedescriptionofthecriticalbehav-ior,associatedwithquantumphasetransitions.Quiterecently,however,averyprecisetuningofparameterswasachievedinasystemofultra-coldatomstrappedinanopticallattice,formedbytheintersectionoflaserbeams[2].AtransitionfromMottinsulatingphasetoasuper?uidphasewasobserved.ItwasarguedthatthesystemiswelldescribedbythebosonicHubbardmodelonad-dimensionallattice,andcomparisonsweremadewithnumericalsimulations[3,4].Thisisjustoneexam-pleofanexperimentalrealizationofastronglycorrelatedquantumsystem,andalotofexperimentalworkwillbedonealongtheselinesinthenearestfuture.Webelievethatitisveryimportantinsuchstudiestobeabletopro-videanaccurateandsimpletheoreticaldescriptionoftheexperimentalsystem.Sincetheanalyticalsolutionofthemodelsofstronglycorrelatedsystemsisusuallyimpos-sible,suchadescriptionmaybeinmostcasesprovidedonlybythenumericalsimulations.Whilee?cientandpowerfulQuantumMonteCarlo(QMC)algorithmsexistforgeneralquantumspinsys-tems,theprogressinthedevelopmentofthealgorithms
forthenumericalsimulationsofbosonicsystemswithno
hardcoreismuchmoremodest.Inthepresentpaper
wedescribeanovelQMCalgorithm,allowinge?cient
simulationsofthebosonicmodelswithshort-rangein-
transformationwhichleavesuswith
b=
1
S?2S
andb?=
1
2S
S+.(1)
Mapping(1)

allows

torewritetheHamiltonianofa
bosonicmodelintermsofspinoperators.Thus,ifthereisanalgorithmforspinsystemswitharbitraryS,andifthein?niteSlimitofthisalgorithmexists,wecaneasilyobtainanalgorithmforthebosonicsystems.
Todemonstratethisidea,weconsiderasimplemodelofnon-interactingsoftcorebosonsonad-dimensionalhy-percubiclatticeoflinearsizeLwiththeHamiltonian
H=?
t
4S
????S+iS?j+S+jS?i???μ??Sz
i.
(3)
??ij??
i
SincethisisanXYspinmodel,ane?cientalgorithm
isavailableforanyS[5].Ourtaskis,therefore,totakethein?niteSlimitofthealgorithm.Itturnsoutthatalltheparametersde?ningthecoarse-grainedalgorithmhavewell-de?nedvaluesinthislimitaswell.Belowwedescribetheprocedureoftakingthislimitandgiveade-taileddescriptionofthesoftcorebosonalgorithmforthenon-interactingmodel.Generalizationstomodelswithinteractions,suchastheon-siterepulsiveinteractionandshortrangedrepulsiveand/orattractiveinteractions,arestraightforward.This,forinstance,makesthepresentideareadilyapplicabletothebosonHubbardmodel.Naturally,bosonoccupationnumbermustbepositive,whichleadstoarestrictiononthepossiblevaluesofchemicalpotential:μ<?dtor|μ|>dt.Toapplythecoarse-grainedalgorithmwecanusethevaluesofparam-eters,derivedforthegeneralXXZmodelinTableIofRef.5.RelationshipbetweentheparametersinRef.5andtheparametersofourmodelis
h=?
|μ|
2S,J′=0.
(4)
OnehastousetheresultsofRef.5withcaution,sincetheyaregivenforthecaseofpositiveh.Therefore,inordertousethemforthepresentproblem,weneedtochangethesignofthe?eldin(4)andatthesametimereinterpretparticlenumbersdenotedbylandminRef.5.Namely,inthepresentarticleldenotesthenumberofholes,whereasˉl≡2S?ldenotesthenumberofparticles.Accordingly,whiletakingthein?niteSlimitwith?xeddensityofparticleswehavetoassumethatlandmarecloseto2S,whereasˉlandmˉareoforderunity.
2
Probabilityofcreationofapairofspin-raisingorparticle-number-decreasing(PND)wormsinthecoarse-grainedalgorithmisˉl/2Sandthatofapairofloweringorparticle-number-increasing(PNI)onesisl/2S.BytakingthelimitS→∞we?nd,thattheprobabilitytocreateapairofPNDwormsiszero.CorrespondingprobabilityforapairofPNIwormsisthenunity,indicatingthatourcyclewillalwaysstartwithapairofPNIworms.That,however,doesnotmeanthatthenumberofparticleswillbeconstantlyincreasing,sincethewormchangesitstypetotheoppositeoneeverytimeitchangesdirectionasaresultofscatteringonavertex.Oncethetravelingwormreturnstothepointoforigin,itcaneitherannihilatethere,endingthecycle,orpassthrough.TheprobabilityofannihilationofapairofPNDwormsis1/ˉlandzeroforthePNIones.
Remainingparameters,suchasdensityofverticesandthevertexscatteringprobabilities,neededforthecon-structionofthealgorithm,canbederivedbyexaminingthevaluesinTableIofRef.5forregionIVandtakingthevalueofStoin?nity.Firstofˉall,thevertexdensityBisgivenbyB=h(lm+lmˉ+lm)/2.Tolistnon-zeroscatteringprobabilities,usingthenotationofRef.5,wehave
PP????↓??
??????lm
??
l?m??=2S(h?J)/(2B),(5)??lm
??=mJ/P???????(2B),(6)??
l?m??lm
??=mJ/ˉ(2B),(7)P??→???
????????l++1??l?mm
l??=1/ˉl,(8)P??→??
m+1??l?1m
??=1/l.(9)wehave????l?m?1
HeresetJ′=0andthesuperscript+or?indi-catesthatthetypeoftheincomingwormisPNDorPNI
respectively.Seemingly,thereisaproblemwithdensityofverticesbecomingin?niteinthein?niteSlimit.How-ever,itshouldbenotedthatallnon-trivialprobabilitiesofthescatteringeventsareproportionalto1/B,sothatthedensityofthescatteringeventsremains?nite.Inotherwords,inthelimitofin?niteSthesituationisiden-ticaltotheonethatoccurswhentakingthecontinuousimaginarytimelimitinaconventionalloopalgorithm[7].Exploitingtheanalogytothecontinuousimaginarytimeloopalgorithm,wecaneasilyconstructaprocedurefor?ndingthetimeofthenextscatteringevent.Namely,in-steadofexaminingeachvertex,itispossibletogeneratethetimeofnexteventasaPoisson-distributedrandomnumberwheretheaveragetimeintervalorthedensitydependsonthelocalspincon?gurationandthetypeofthescatteringprocess.
Wecanreadilyobtainthedensityofsucheventsbymultiplyingthescatteringprobabilities(5),(6)and(7)byBandtakethein?niteSlimit.SinceEq.(7)yields
3
3
zero,wehavetwonon-zeroscatteringdensitiesforinter-valsthathavenokinksinit:
Λ??↓??
??????lml?m
??=|μ|?dt
2.
(11)
Forthescattering

probabilityatkinks,onlythescat-teringprobability(8)willremainnon-zero,sincetheprobability(9)vanishesinthein?niteSlimit.
Inordertodescribethealgorithmindetail,weintro-duceaconceptofaconstantenvironmentinterval(CEI)onwhichthemovingwormresides.ACEIisde?nedasanintervalaheadoftheworminwhichtheenvironmentofthewormdoesnotchangeintheimaginarytimedi-rection,i.e.,theworldlinestatechangesneitheronthecurrentsitenoronanyoftheneighboringsites.Thisintervalisboundedbyoneofthreeevents,closesttotheworm:a)akinkonthecurrentsite,b)akinkononeoftheneighboringsites,orc)thepointoforigin,wheretheotherwormwaitsforthemovingworm.
Worldlinecon?gurationupdatecycleforthenon-interactingmodelmaybesummarizedasfollows:1)Chooseanarbitraryspace-timepointtoplaceapairofworms,oneofwhichwillmove,producingthechangesinthecon?guration,andanotheronewillmarkthepointoforigin.AlwaysstartwithaPNI(spin-lowering)worm.Choosethearbitrarydirection(upordown)fortheworm’sinitialmovement.2)DeterminetheCEI.
3)Foreachtypeofscatteringandforeachnearestneigh-borsite,whichisacandidateforthe?nalscatteringdes-tination,generatethetimeofthenextpossiblescatteringeventstochasticallyaccordingtothePoissondistributionwiththedensities(10)and(11).
4)IftheadvancementofthewormbythesmallestofthesetimesdoesnottakethewormoutofCEI,imple-mentthecorrespondingscatteringevent.Incaseofaback-scatteringevent,changethetypeofthewormtotheoppositeone.Gobackto2.
4’)IftheadvancementofthewormgetthewormoutofCEI,advancethewormtotheendoftheCEI.
5)IftheendpointoftheCEIisnotakinkortheoriginalstartingpoint,gobackto2.
5’)IftheendpointoftheCEIisakink,attempttoscat-teronitaccordingto(8).Ifthescatteringfailsornotapplicable,letthewormskipthekinkandgoon.Gobackto2.
5”)IftheendpointoftheCEIistheoriginalstartingpoint,stochasticallydetermine,whethertheywillanni-hilatewiththeprobability1/ˉlwhereˉlistheparticlenumberontheCEI.Ifitannihilates,theupdatecycleisterminated.Otherwisegobackto2.
10102
101
κ100
10?1
10
?2
00.20.4
0.60.81
n
FIG.1:Thecompressibilityplottedagainsttheaverageoc-cupationnumberforthree-dimensionalfreelatticebosonsys-tematkBT/t=2.0.Thelinesaretheexactanalyticalvalues,whilethesymbolsaretheresultsofQMCsimulation.Uncer-taintyintheoccupationnumberisinallcasessmallerthanthewidthofthesymbols.DataforL=16and??n??>0.4iscomputedwiththestandardnumberofcycles(soliddia-monds),whilethedatafor??n??≤0.4wasobtainedwitha100timeslongersimulation(opendiamonds).Errorbarsareinallcasessmallerthanthesizeofthesymbols.
Afteranumberoffullupdatecycles(resultinginwormannihilation)theobservablesaremeasured.
Totestthevalidityandevaluatethee?ciencyofthealgorithmwehaveperformedanumberoftests,compar-ingtheresultsofQMCsimulationofthenon-interactingbosonmodelinthreedimensionstotheexactresults.Al-thoughthemodeldoesnothaveanyinteractionterms,itisnon-trivialenoughtoprovideuswithexcellentgroundsfortestingbecauseitdisplaysBose-Einsteincondensation(BEC)andtheobservablesmaybecalculatedanalyti-cally.
WehaveperformedsimulationsatkBT=2tat10dif-ferentvaluesofthechemicalpotential,chosensothattheresultingaverageoccupationnumberwouldben≡??areN??/Vconsidered:=0.1,0.2L,...=,14.,0.8,16.ThreeIfdi?erentnotstatedsystemotherwise,sizesforeachvalueofsystemsizeandchemicalpotentialwehaveperformed50,000cyclesforequilibration,andan-other50,000cyclesformeasurement.The50,000mea-surementscyclesweredividedinto10binsoftheequallengthforestimatingthestatisticalerror.
Inallcasesweinvestigated,includingcasesclosetocriticalityandonesdeepinsidethesuper?uidphase,wefoundanexcellentagreementbetweenthenumeri-calQMCdataandtheexactanalyticalresults.Asanexample,Fig.1showsthedependence2ofthecompress-ibilityκ≡(?n/?μ)T=(kBT)?1(??Nofnata?xedtemperature??k?BT??N=??2)/Ldasafunction2t.The
4
inprinciple,toanyquantumsystem.However,itisuptotheuserto?ndasetofscatteringprobabilities,opti-mizingthee?ciencyofthealgorithmforagivenmodel.Duetoahugefreedominthechoiceofalgorithmpa-rameters,inmostcasesthisisahighlynontrivialtask.Inaddition,toapplythedirectedloopalgorithmtothesoftcorebosonsystems,onehastosetanarti?cialup-perboundforthesiteoccupationnumber.Thisupperboundmustbetakenlargeenoughtomakethesimu-lationfreefromthesystematicerror.Thiscouldbeaseriousdisadvantageespeciallyforbosonicsystemwitharandomchemicalpotentialwherealargenumberofparticlesmayresideonthesamesite.Thepresentalgo-rithmisfreefromthesedisadvantages.Forcomparisonpurposeswehaveusedthedirectedloopalgorithmwithasetofsimpleheat-bathscatteringprobabilitiesandthesiteoccupationnumberwaslimitedbyni≤20.
Whileitishardtomakeaquantitativecomparisonoftwoessentiallydi?erentalgorithms,wehaveestablishedthatourproposedalgorithminallconsideredcasesper-formsbetter,i.e.inallcasessmallercomputationaltimewasneededtoreachthesameerrorbars.Whilethecom-parisonofcomputationaltimesdoesnotinequivocallyprovethatouralgorithmismoree?cient,wenotethatinthevicinityofthecriticalpointandinthesuper?uidphasewehavefailedtoobtainthereliableestimatesfortheobservableswiththedirectedloopalgorithmwithinreasonablecomputationaltime.
Insummary,wehavedescribedaconstructionofane?cientQMCalgorithmforthesimulationofsoftcorebosonmodelsonthelattice,basedonthecoarse-grainedalgorithmsforthespinmodels.Byestablishingthere-lationshipbetweenthebosonandspinoperatorsinthein?niteS(totalspinquantumnumber)limit,wehavemappedthemodelofnon-interactingbosonsonalatticetoaspinXY-modelinamagnetic?eld.Wehavedemon-strated,thatthelimitofin?niteSmaybetakendirectlyinthealgorithm,leadingtoimprovedperformanceandabsenceofsystematicerrors.Theresultingalgorithmwasfoundtoperformbetterthanexistingalgorithms.Theresultofapplicationsofthepresentalgorithmtoothermodels,suchastheBoseHubbardmodel,willbereportedelsewhere[10].
WearegratefultotheSwedishNationalAllocationCommittee(SNAC)andNationalSupercomputerCenterinLink¨oping(Sweden)forprovidingcomputertimeusedforamajorpartoftestingandsimulations.NK’sworkissupportedbyGrants-in-AidforScienti?cResearchPro-ˇgrate-gram(#14540361)fromMonka-sho,Japan.JS
fullyacknowledges?nancialsupportfromtheSwedishFoundationforStrategicResearch.
0.6
0.4ρS
0.20n
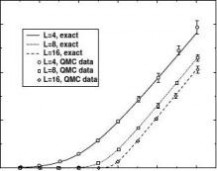
FIG.2:Thesuper?uiddensityplottedagainsttheaverageoccupationnumberforthree-dimensionalfreelatticebosonsystem.Standardsimulationparameterswereusedforalldatapoints.ThelinesaretheexactanalyticalvalueswhilethesymbolsaretheresultsofQMCsimulation.
observationofthedivergentbehaviorofcompressibilityatBECtransitioniswellwithinthereachofnumericalsimulation.ForlowvaluesofnandL=16wehadtoin-creasethenumberofcycles100timesinordertoobtainagoodstatisticsbecausethetypicallifetimeofawormbecomestooshortinthiscase.Evenafterthisincrease,theCPUtimespentforthiscaseissmallerthanthatforthesuper?uidcases.
InFig.2,weplotthesuper?uiddensityρSagainsttheaverageoccupationnumber.ρSisde?ned[8]as??2???d2
ρS≡LkBTdF(θ)/dθθ=0whereF(θ)isthefreeenergyofasystemtwistedbytheangleθperlatticespac-ing.InQMCsimulationthisquantitycanbemeasured
2
byρS=L2?dkBT??Wx??whereWxisthesumofwindingnumbersofallworldlinesinthex-direction.Thepossi-bilityofmeasuringthewindingnumber?uctuationisoneoftheadvantagesofthepresentapproach,comparedtothealgorithms,suchastheoneusedinRef.4,thatworksinthe?xedwindingnumberensemble.InFig.2,wecanagainseethattheonsetofthecondensationiscapturedbytheQMCsimulationwiththepresentalgorithm.Wehavealsocomparedtheperformanceofthenewal-gorithmwiththedirectedloopalgorithm[9],oneofthebestQMCalgorithmscurrentlyavailableforthesimula-tionofsoftcorebosonsystems.Thedirectedloopalgo-rithmisquitegeneralandpowerfulmethod,applicable,
[1]S.Sachdev,QuantumPhaseTransitions(Cambridge
UniversityPress,1999).
[2]M.Greineretal.,Nature415,39(2002).
[3]V.A.Kashurnikov,N.V.Prokof’ev,andB.V.Svistunov,arXiv:cond-mat/0202510.
[4]G.G.Batrounietal.,arXiv:cond-mat/0203082.
[5]K.HaradaandN.Kawashima,Phys.Rev.E66,056705
(2002).
5
[6]J.HolsteinandN.Primako?,Phys.Rev.58,1098(1940).
[7]B.B.BeardandU.-J.Wiese,Phys.Rev.Lett.77,5130
(1996).
[8]E.L.PollockandD.M.Ceperley,Phys.Rev.B36,8343
(1987).[9]O.F.Sylju?asenandA.W.Sandvik,Phys.Rev.E66,046701(2002).ˇ[10]J.Smakov,K.Harada,andN.Kawashima(unpublished).
本文标题:a song for mama-A present for mother61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1