一 : 大学数学公式总结大全
高等数学公式大全 此系列公式适合现行大学高等数学通用教材
导数公式:
(tgx)??sec2x(arcsinx)??1(ctgx)???csc2x?x2(secx)??secx?tgx(arccosx)???1(cscx)???cscx?ctgx?x2(ax)??axlna(arctgx)??1
1?x2
(log1
ax)??xlna(arcctgx)???1
1?x2
基本积分表:
?tgxdx??lncosx?CC??dxctgxdx?lnsinx?Ccos2x??sec2xdx?tgx??secxdx?lnsecx?tgx?C?dx2
sin2x??cscxdx??ctgx?C
?cscxdx?lncscx?ctgx?C?secx?tgxdx?secx?C?dx?cscx?ctgxdx??cscx?Ca2?x2?1aarctgx
a?C
?dx1x??axdx?ax
lna?C
x2?a2?2alna
x?a?C?shxdx?chx?C?dx
a2?x2?1a?x2alna?x?C?chxdx?shx?C?dx
a2?x2?arcsinxa?C?dx
x2?a2?ln(x?x2?a2)?C
??
22
In
n??sinxdx??cosnxdx?n?100nIn?2
?x2?a2dx?x22a2
2x?a?2ln(x?x2?a2)?C?x?adx?x22222a
2x?a?2lnx?x2?a2?C?a2?x2dx?x22a2x
2a?x?2arcsina?C
三角函数的有理式积分:
sinx?2u1?u2x2du
1?u2cosx?1?u2u?tg2, dx?1?u2 - 1 -
高等数学公式大全
此系列公式适合现行大学高等数学通用教材
一些初等函数:
两个重要极限:
x?x
双曲正弦:shx?e?e
2limsinx
x?0x?1
chx?ex?e?x
双曲余弦:2limx??(1?1x)x?e?2.718281828459045...
双曲正切:thx?shxex?e?x
chx?ex?e?x arshx?ln(x?x2?1)
archx??ln(x?x2?1) arthx?11?x
2ln1?x
三角函数公式:
·诱导公式:
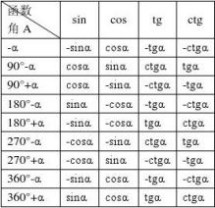
·和差角公式: ·和差化积公式: sin(???)?sin?cos??cos?sin?sin??sin??2sin???cos(???)?cos?cos??sin?sin?2cos???
2
tg(???)?tg??tg?sin??sin??2cos??????
1?tg??tg?2sin2
cos??cos??2cos??????
ctg(???)?ctg??ctg??12cos2
ctg??ctg?cos??cos??2sin??????
2sin2
- 2 -
高等数学公式大全
此系列公式适合现行大学高等数学通用教材
·倍角公式:
sin2??2sin?cos?
cos2??2cos2??1?1?2sin2??cos2??sin2?sin3??3sin??4sin3?ctg2??ctg2??1cos3??4cos3??3cos?
2ctg?tg3??3tg??tg3?
tg2??2tg?1?3tg2?
1?tg2?
·半角公式:
sin??cos?1
2??2 cos2???cos2
tg???1?cos?1?cos?sin??1?cos?1?cos?
21?cos??sin??1?cos? ctg2??1?cos??sin??sin?
1?cos?
·正弦定理:a?b
sinB?c
sinC?2R·余弦定理:c2
sinA?a2?b2?2abcosC
·反三角函数性质:arcsinx??
2?arccosx arctgx??
2?arcctgx
高阶导数公式——莱布尼兹(Leibniz)公式:
(uv)(n)n
??Cku(n?k)v(k)
n
k?0 ?u(n)v?nu(n?1)v??n(n?1)(n?2)n(n?1)?(n?k?
2!uv?????1)(n?k)(k)
k!uv???uv(n)
中值定理与导数应用:
拉格朗日中值定理:f(b)?f(a)?f?(?)(b?a)
f(b)?f(a)f?(?)
F(b)?F(a)?F?(?)
当F(x)?x时,柯西中值定理就是拉格朗日中值定理。
曲率:
弧微分公式:ds??y?2dx,其中y??tg?平均曲率:K???
?s??:从M点到M?点,切线斜率的倾角变化量;?s:MM?弧长。M点的曲率:K??lim??s?0?s?d?
ds?y??
(1?y?2)3.
直线:K?0;
半径为a的圆:K?1
a.
- 3 -
高等数学公式大全 此系列公式适合现行大学高等数学通用教材
定积分的近似计算:
b
矩形法:?f(x)?b?a
n(y0?y1???yn?1)
a
b
梯形法:?f(x)?b?a
an[12(y0?yn)?y1???yn?1]
b
抛物线法:?f(x)?b?a
a3n[(y0?yn)?2(y2?y4???yn?2)?4(y1?y3???yn?1)]
定积分应用相关公式:
功:W?F?s
水压力:F?p?A
引力:F?km1m2
r2,k为引力系数
函数的平均值:y?1b
b?a?f(x)dx
a
b
1
b?a?f2(t)dt
a
空间解析几何和向量代数:

空间2点的距离:d?M1M2?(x2?x1)2?(y2?y22
1)?(z2?z1)
向量在轴上的投影:Prju?cos?,?是与u轴的夹角。Prj??a???
u(a12)?Prja1?Prja
a??b??a??b?2
cos??axbx?ayby?azbz,是一个数量,两向量之间的夹角:cos??axbx?ayby?azbz
a2222
x?ay?az?bx?b22
y?bz
ijk
c??a??b??axaya,c??a??b?sin?.例:线速度:v??w??r?
z.bxbybz
ay
向量的混合积:[a?b?axaz
c?]?(a??b?)?c??bxbyba??b??c?
z?cos?,?为锐角时,cxcycz
代表平行六面体的体积。
- 4 -
高等数学公式大全
此系列公式适合现行大学高等数学通用教材
平面的方程:
1、点法式:A(x?x(y?y,其中n?
0)?B0)?C(z?z0)?0?{A,B,C},M0(x0,y0,z0)
2、一般方程:Ax?By?Cz?D?0
3xyz
a?b?c?1
平面外任意一点到该平面的距离:d?Ax0?By0?Cz0?D
A2?B2?C2
x?x0
m?y?y?x?x0?mt
n?z?z0
p?t,其中?s?{m,n,p};参数方程:??y?y
?0?nt
?z?z0?pt
二次曲面:
x2y2z2
1a2?b2?c2?1
x2y2
22p?2q?z(,p,q同号)
3、双曲面:
x2y2z2
a2?b2?c2?1
x2y2z2
a2?b2?c2?(马鞍面)1
多元函数微分法及应用
全微分:dz??z
?xdx??z
?ydy du??u?u?u
?xdx??ydy??zdz
全微分的近似计算:?z?dz?fx(x,y)?x?fy(x,y)?y多元复合函数的求导法:
z?f[u(t),v(t)]dz?z?u?z?v
dt??u??t??v??t
z?f[u(x,y),v(x,y)]?z?z?u?z?v
?x??u??x??v??x
当u?u(x,y),v?v(x,y)时,
du??u
?xdx??u
?ydy dv??v
?xdx??v
?ydy
隐函数的求导公式:
隐函数F(x,y)?0dyFxd2y?F?Fdy
dx??Fx
2?(?+(?x?
ydx?xFy?yFydx
隐函数F(x,y,z)?0?zFx?zFy
?x??F??
z?yFz
- 5 -
高等数学公式大全
此系列公式适合现行大学高等数学通用教材
?F
?F(x,y,u,v)?0?(F,G)?u
隐函数方程组: J????GG(x,y,u,v)?0?(u,v)?
?u
?u1?(F,G)?v1?(F,G)???????xJ?(x,v)?xJ?(u,x)?u1?(F,G)?v1?(F,G)???????yJ?(y,v)?yJ?(u,y)
微分法在几何上的应用:
?F
?v?Fu?GGu?v
FvGv
?x??(t)
x?xy?y0z?z0?
空间曲线?y??(t)在点M(x0,y0,z0)0??
??(t0)??(t0)??(t0)?z??(t)
?
在点M处的法平面方程:??(t0)(x?x0)???(t0)(y?y0)???(t0)(z?z0)?0??FyFzFzFxFx?F(x,y,z)?0
若空间曲线方程为:,则切向量T?{,,?
GGGxGGG(x,y,z)?0?yzzx?
曲面F(x,y,z)?0上一点M(x0,y0,z0),则:
?
1、过此点的法向量:n?{Fx(x0,y0,z0),Fy(x0,y0,z0),Fz(x0,y0,z0)}x?x0y?y0z?z0
3??
Fx(x0,y0,z0)Fy(x0,y0,z0)Fz(x0,y0,z0)
方向导数与梯度:
FyGy
2、过此点的切平面方程:Fx(x0,y0,z0)(x?x0)?Fy(x0,y0,z0)(y?y0)?Fz(x0,y0,z0)(z?z0)?0
?f?f?f
函数z?f(x,y)在一点p(x,y)沿任一方向l?cos??sin?
?l?x?y其中?为x轴到方向l的转角。
函数z?f(x,y)在一点p(x,y)的梯度:gradf(x,y)?
?f??f?i?j?x?y
???f??
它与方向导数的关系是?gradf(x,y)?e,其中e?cos??i?sin??j,为l方向上的
?l
单位向量。
?f
是gradf(x,y)在l上的投影。?l
?
多元函数的极值及其求法:
设fx(x0,y0)?fy(x0,y0)?0,令:fxx(x0,y0)?A, fxy(x0,y0)?B, fyy(x0,y0)?C??A?0,(x0,y0)为极大值2AC?B?0时,??
?A?0,(x0,y0)为极小值??2
则:?AC?B?0时, 无极值?AC?B2?0时, 不确定???
- 6 -
高等数学公式大全
此系列公式适合现行大学高等数学通用教材
重积分及其应用:
??f(x,y)dxdy???f(rcos?,rsin?)rdrd?
D
D?
曲面z?f(x,y)的面积A???
D
??z???z????????y??dxdy?x????
2
2
?
Mx?M
??x?(x,y)d?
D
???(x,y)d?
D
D
, ?
MyM
?
??y?(x,y)d?
D
???(x,y)d?
D
D
平面薄片的转动惯量:对于x轴Ix???y2?(x,y)d?, 对于y轴Iy???x2?(x,y)d?平面薄片(位于xoy平面)对z轴上质点M(0,0,a),(a?0)的引力:F?{Fx,Fy,Fz},其中:Fx?f??
D
?(x,y)xd?
(x?y?a)
2
2
22
Fy?f??3
D
?(x,y)yd?
(x?y?a)
2
2
22
Fz??fa??3
D
?(x,y)xd?
(x?y?a)
2
2
3
22
柱面坐标和球面坐标:
?x?rcos??
柱面坐标:f(x,y,z)dxdydz????F(r,?,z)rdrd?dz,?y?rsin?, ??????z?z
?
其中:F(r,?,z)?f(rcos?,rsin?,z)
?x?rsin?cos??2
球面坐标:?y?rsin?sin?, dv?rd??rsin??d??dr?rsin?drd?d?
?z?rcos??
2?
?r(?,?)
???f(x,y,z)dxdydz????F(r,?,?)r
?
?
2
sin?drd?d???d??d?
?F(r,?,?)r
2
sin?dr
?
1M
???x?dv, ?
?
?
1M
???y?dv, ?
?
?
1M
???z?dv, 其中M??????dv
?
?
?
转动惯量:Ix????(y2?z2)?dv, Iy????(x2?z2)?dv, Iz????(x2?y2)?dv
曲线积分:
第一类曲线积分(对弧长的曲线积分):
?x??(t)
设f(x,y)在L上连续,L的参数方程为:, (??t??),则:?
?y??(t)
?
L
?x?t22
??f(x,y)ds??f[?(t),?(t)](t)??(t)dt (???) 特殊情况:?
?y??(t)?
?
- 7 -
高等数学公式大全
此系列公式适合现行大学高等数学通用教材
第二类曲线积分(对坐标的曲线积分):
?x??(t)设L的参数方程为?,则:y??(t)?
?
?P(x,y)dx?Q(x,y)dy?
??{P[?(t),?(t)]??(t)?Q[?(t),?(t)]??(t)}dtL
两类曲线积分之间的关系:?Pdx?Qdy??(Pcos??Qcos?)ds,其中?和?分别为
LL
L上积分起止点处切向量的方向角。
格林公式:??(
D?Q?P?Q?P?)dxdy?Pdx?Qdy格林公式:(?dxdy?Pdx?Qdy???x?y?x?yLDL
?Q?P1当P??y,Q?x??2时,得到D的面积:A???dxdy?xdy?ydx?x?y2LD
·平面上曲线积分与路径无关的条件:
1、G是一个单连通区域;
2、P(x,y),Q(x,y)在G内具有一阶连续偏导数,且
减去对此奇点的积分,注意方向相反!
·二元函数的全微分求积:
?Q?P在时,Pdx?Qdy才是二元函数u(x,y)的全微分,其中:?x?y
(x,y)?Q?P(0,0),应?x?y
u(x,y)?
(x0,y0)?P(x,y)dx?Q(x,y)dy,通常设x0?y0?0。
曲面积分:
22对面积的曲面积分:f(x,y,z)ds?f[x,y,z(x,y)]?z(x,y)?z(x,y)dxdyxy????
?Dxy
对坐标的曲面积分:??P(x,y,z)dydz?Q(x,y,z)dzdx?R(x,y,z)dxdy,其中:
?
??R(x,y,z)dxdy????R[x,y,z(x,y)]dxdy,取曲面的上侧时取正号;?Dxy
??P(x,y,z)dydz????P[x(y,z),y,z]dydz,取曲面的前侧时取正号;?Dyz
??Q(x,y,z)dzdx????Q[x,y(z,x),z]dzdx,取曲面的右侧时取正号。?Dzx
两类曲面积分之间的关系:??Pdydz?Qdzdx?Rdxdy???(Pcos??Qcos??Rcos?)ds
??
高斯公式:
- 8 -
高等数学公式大全
此系列公式适合现行大学高等数学通用教材
???(
??P?Q?R??dv?Pdydz?Qdzdx?Rdxdy?(Pcos??Qcos??Rcos?)ds?x?y?z??
高斯公式的物理意义——通量与散度:
??P?Q?R?散度:div????,即:单位体积内所产生的流体质量,若div??0,则为消失...通量:??A??x?y?z
?n?ds???Ands???(Pcos??Qcos??Rcos?)ds,
???
因此,高斯公式又可写成:???divA?dv?Ands
??
斯托克斯公式——曲线积分与曲面积分的关系:
??(?R?Q?P?R?Q?
??y??z)dydz?(?z??x)dzdx?(?x?P?y)dxdy?Pdx?Qdy?Rdz?
dydzdzdxcos?cos?cos?
上式左端又可写成:????????
??x?y?z????x?y?zPQR?PQR
空间曲线积分与路径无?R?Q?P?R?Q?P
?y??z?z??x?x??y
旋度:rotA?ijk
????
?x?y?z
PQ
向量场A?R沿有向闭曲线?Pdx?Qdy?Rdz?A???tds
??
常数项级数:
?q?q2???qn?1?1?qn
等比数列:11?q
等差数列:1?2?3???n?(n?1)n
2
调和级数:1?111
2?3???n是发散的
级数审敛法:
- 9 -
高等数学公式大全
此系列公式适合现行大学高等数学通用教材
1、正项级数的审敛法——根植审敛法(柯西判别法):
???1时,级数收敛?设:??limn,则???1时,级数发散n?????1时,不确定?
2、比值审敛法:
???1时,级数收敛U?设:??limn?1???1时,级数发散n??Un???1时,不确定?
3、定义法:
sn?u1?u2???un;limsn存在,则收敛;否则发散。n??
交错级数u1?u2?u3?u4??(或?u1?u2?u3??,un?0)的审敛法——莱布尼兹定理:
? ?un?un?1如果交错级数满足?,那么级数收敛且其和s?u1,其余项rn的绝对值rn?un?1。limu?0??n??n
绝对收敛与条件收敛:
(1)u1?u2???un??,其中un为任意实数;
(2)u1?u2?u3???un??
如果(2)收敛,则(1)肯定收敛,且称为绝对收敛级数;如果(2)发散,而(1)收敛,则称(1)为条件收敛级数。
1(?1)n
调和级数:?n发散,而?n1 级数:?n2收敛;
?1时发散1 p级数:?npp?1时收敛
幂级数:
- 10 -
高等数学公式大全
此系列公式适合现行大学高等数学通用教材
1x?1时,收敛于1?x1?x?x2?x3???xn??x?1时,发散
对于级数(3)a0?a1x ?a2x2???anxn??,如果它不是仅在原点收敛,也不是在全
x?R时收敛
数轴上都收敛,则必存在R,使x?R时发散,其中R称为收敛半径。
x?R时不定
1 ??0时,R?
求收敛半径的方法:设liman?1??,其中an,an?1是(3)??0时,R???n??an????时,R?0?函数展开成幂级数:
f??(x0)f(n)(x0)2函数展开成泰勒级数:f(x)?f(x0)(x?x0)?(x?x0)???(x?x0)n??2!n!
f(n?1)(?)余项:Rn?(x?x0)n?1,f(x)可以展开成泰勒级数的充要条件是:limRn?0 n??(n?1)!
f??(0)2f(n)(0)nx0?0时即为麦克劳林公式:f(x)?f(0)?f?(0)x?x???x??2!n!
一些函数展开成幂级数:
m(m?1)2m(m?1)?(m?n?1)nx???x?? (?1?x?1)2!n! 352n?1xxxsinx?x?????(?1)n?1?? (???x???)3!5!(2n?1)!(1?x)m?1?mx?
欧拉公式:
?eix?e?ix
cosx???2eix?cosx?isinx 或? ix?ix?sinx?e?e
?2?
三角级数:
a0?
f(t)?A0??Ansin(n?t??n)???(ancosnx?bnsinnx)2n?1n?1
其中,a0?aA0,an?Ansin?n,bn?Ancos?n,?t?x。正交性:1,sinx,cosx,sin2x,cos2x?sinnx,cosnx?任意两个不同项的乘积在[??,?]上的积分=0。
傅立叶级数: ?
- 11 -
高等数学公式大全
此系列公式适合现行大学高等数学通用教材
a0?
f(x)???(ancosnx?bnsinnx),周期?2?2n?1
??1(n?0,1,2?)?an??f(x)cosnxdx ????其中???b?1f(x)sinnxdx (n?1,2,3?)?n?????
11?2
1?2?2???835 111?2
?2?2???224246
正弦级数:an?0,bn?
余弦级数:bn?0,an?111?21?2?2?2???6234111?21?2?2?2???12234f(x)sinnxdx n?1,2,3? f(x)??b??02?nsinnx是奇函数2?
??0f(x)cosnxdx n?0,1,2? f(x)?a0??ancosnx是偶函数2
周期为2l的周期函数的傅立叶级数:
a0?n?xn?xf(x)???(ancos?bnsin),周期?2l2n?1ll
l?1n?xdx (n?0,1,2?)?an??f(x)cosl?ll?其中?l?b?1f(x)sinn?xdx (n?1,2,3?)?nl?l?l?
微分方程的相关概念:
阳光怡茗工作室http://ygymlove.taobao.com
一阶微分方程:y??f(x,y) 或 P(x,y)dx?Q(x,y)dy?0
可分离变量的微分方程:一阶微分方程可以化为g(y)dy?f(x)dx的形式,解法:?g(y)dy??f(x)dx 得:G(y)?F(x)?C称为隐式通解。
dyy?f(x,y)??(x,y),即写成的函数,解法:
dxx
ydydududxduy设u??u?x,u???(u),??分离变量,积分后将代替u,xdxdxdxx?(u)?ux齐次方程:一阶微分方程可以写成即得齐次方程通解。
一阶线性微分方程:
- 12 -
高等数学公式大全
此系列公式适合现行大学高等数学通用教材
dy1?P(x)y?Q(x)dx
?P(x)dx当Q(x)?0时,为齐次方程,y?Ce?
P(x)dx?P(x)dx当Q(x)?0时,为非齐次方程,y?(?Q(x)e?dx?C)e?
dy2?P(x)y?Q(x)yn,(n?0,1)dx
全微分方程:
如果P(x,y)dx?Q(x,y)dy?0中左端是某函数的全微分方程,即:
?u?udu(x,y)?P(x,y)dx?Q(x,y)dy?0?P(x,y)?Q(x,y) ?x?y
?u(x,y)?C应该是该全微分方程的通解。
二阶微分方程:
f(x)?0时为齐次d2ydy?P(x)?Q(x)y?f(x) dxdx2f(x)?0时为非齐次
二阶常系数齐次线性微分方程及其解法:
(*)y???py??qy?0,其中p,q为常数;
求解步骤:
1、写出特征方程:(?)r2?pr?q?0,其中r2,r的系数及常数项恰好是(*)式中y??,y?,y的系数;
2、求出(?)式的两个根r1,r2

3、根据r1,r2的不同情况,按下表写出(*)式的通解:
二阶常系数非齐次线性微分方程
y???py??qy?f(x),p,q为常数
f(x)?e?xPm(x)型,?为常数;
f(x)?e?x[Pl(x)cos?x?Pn(x)sin?x]型
- 13 -
高等数学公式大全
此系列公式适合现行大学高等数学通用教材
概率公式部分
1.随机事件及其概率
A????A???A
吸收律:A???AA???? A?(AB)?AA?(A?B)?A
A?B?A?A?(AB)
反演律:A?B?AB??
nnnn
?Ai??Ai?Ai??Ai
i?1i?1i?1i?1
2.概率的定义及其计算
P(?1?P(A)
若A?B?P(B?A)?P(B)?P(A)
对任意两个事件A, B, 有P(B?A)?P(B)?P(AB)
加法公式:对任意两个事件A, B, 有
P(A?B)?P(A)?P(B)?P(AB)
P(A?B)?P(A)?P(B)
n
P(?nn
Ai)??P(Ai)?An?1
iAj)?jkP(A1A2?An)
i?1i?11?i?P(?j?n1?i??P(AiAA)???(?1)j?k?n
3.条件概率
P?BA??P(AB)
P(A)
乘法公式
- 14 -
二 : 高中数学公式总结
数学公式贯穿于整个高中数学的学习过程中,学好数学公式是学好数学的关键。但是高中数学公式在课本中的位置可以说是分布的比较分散,很多同学嫌麻烦懒得整理,结果导致考试的时候因为公式的原因失分。为了方便大家,小编为大家整理了高中数学公式总结。
一、数学知识口诀
1、集合与函数
内容子交并补集,还有幂指对函数。性质奇偶与增减,观察图象最明显。
复合函数式出现,性质乘法法则辨,若要详细证明它,还须将那定义抓。
指数与对数函数,两者互为反函数。底数非1的正数,1两边增减变故。
函数定义域好求。分母不能等于0,偶次方根须非负,零和负数无对数;
正切函数角不直,余切函数角不平;其余函数实数集,多种情况求交集。
两个互为反函数,单调性质都相同;图象互为轴对称,Y=X是对称轴;
求解非常有规律,反解换元定义域;反函数的定义域,原来函数的值域。
幂函数性质易记,指数化既约分数;函数性质看指数,奇母奇子奇函数,
奇母偶子偶函数,偶母非奇偶函数;图象第一象限内,函数增减看正负。
2、三角函数
三角函数是函数,象限符号坐标注。函数图象单位圆,周期奇偶增减现。
同角关系很重要,化简证明都需要。正六边形顶点处,从上到下弦切割;
中心记上数字1,连结顶点三角形;向下三角平方和,倒数关系是对角,
顶点任意一函数,等于后面两根除。诱导公式就是好,负化正后大化小,
变成税角好查表,化简证明少不了。二的一半整数倍,奇数化余偶不变,
将其后者视锐角,符号原来函数判。两角和的余弦值,化为单角好求值,
余弦积减正弦积,换角变形众公式。和差化积须同名,互余角度变名称。
计算证明角先行,注意结构函数名,保持基本量不变,繁难向着简易变。
逆反原则作指导,升幂降次和差积。条件等式的证明,方程思想指路明。
万能公式不一般,化为有理式居先。公式顺用和逆用,变形运用加巧用;
1加余弦想余弦,1减余弦想正弦,幂升一次角减半,升幂降次它为范;
三角函数反函数,实质就是求角度,先求三角函数值,再判角取值范围;
利用直角三角形,形象直观好换名,简单三角的方程,化为最简求解集;
3、不等式
解不等式的途径,利用函数的性质。对指无理不等式,化为有理不等式。
高次向着低次代,步步转化要等价。数形之间互转化,帮助解答作用大。
证不等式的方法,实数性质威力大。求差与0比大小,作商和1争高下。
直接困难分析好,思路清晰综合法。非负常用基本式,正面难则反证法。
还有重要不等式,以及数学归纳法。图形函数来帮助,画图建模构造法。
4、数列
等差等比两数列,通项公式N项和。两个有限求极限,四则运算顺序换。
数列问题多变幻,方程化归整体算。数列求和比较难,错位相消巧转换,
取长补短高斯法,裂项求和公式算。归纳思想非常好,编个程序好思考:
一算二看三联想,猜测证明不可少。还有数学归纳法,证明步骤程序化:
首先验证再假定,从K向着K加1,推论过程须详尽,归纳原理来肯定。

二、三角函数
两角和公式
sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosA
cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB
tan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)
cot(A+B)=(cotAcotB-1)/(cotB+cotA)cot(A-B)=(cotAcotB+1)/(cotB-cotA)
倍角公式
tan2A=2tanA/(1-tan2A)cot2A=(cot2A-1)/2cota
cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a
sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0
cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2
tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0
四倍角公式
sin4A=-4*(cosA*sinA*(2*sinA^2-1))
cos4A=1+(-8*cosA^2+8*cosA^4)
tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)
五倍角公式
sin5A=16sinA^5-20sinA^3+5sinA
cos5A=16cosA^5-20cosA^3+5cosA
tan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)
六倍角公式
sin6A=2*(cosA*sinA*(2*sinA+1)*(2*sinA-1)*(-3+4*sinA^2))
cos6A=((-1+2*cosA^2)*(16*cosA^4-16*cosA^2+1))
tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA^2-15*tanA^4+tanA^6)
七倍角公式
sin7A=-(sinA*(56*sinA^2-112*sinA^4-7+64*sinA^6))
cos7A=(cosA*(56*cosA^2-112*cosA^4+64*cosA^6-7))
八倍角公式
sin8A=-8*(cosA*sinA*(2*sinA^2-1)*(-8*sinA^2+8*sinA^4+1))
cos8A=1+(160*cosA^4-256*cosA^6+128*cosA^8-32*cosA^2)
九倍角公式
sin9A=(sinA*(-3+4*sinA^2)*(64*sinA^6-96*sinA^4+36*sinA^2-3))
cos9A=(cosA*(-3+4*cosA^2)*(64*cosA^6-96*cosA^4+36*cosA^2-3))
万能公式
sinα=2tan(α/2)/[1+tan^2(α/2)]
cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]
tanα=2tan(α/2)/[1-tan^2(α/2)]
半角公式
sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2)
cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2)
tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))
cot(A/2)=√((1+cosA)/((1-cosA))cot(A/2)=-√((1+cosA)/((1-cosA))
三、相关推论及定理
1过两点有且只有一条直线
2两点之间线段最短
3同角或等角的补角相等
4同角或等角的余角相等
5过一点有且只有一条直线和已知直线垂直
6直线外一点与直线上各点连接的所有线段中,垂线段最短
7平行公理经过直线外一点,有且只有一条直线与这条直线平行
8如果两条直线都和第三条直线平行,这两条直线也互相平行
9同位角相等,两直线平行
10内错角相等,两直线平行
11同旁内角互补,两直线平行
12两直线平行,同位角相等
13两直线平行,内错角相等
14两直线平行,同旁内角互补
15定理三角形两边的和大于第三边
16推论三角形两边的差小于第三边
17三角形内角和定理三角形三个内角的和等于180°
18推论1直角三角形的两个锐角互余
19推论2三角形的一个外角等于和它不相邻的两个内角的和
20推论3三角形的一个外角大于任何一个和它不相邻的内角
21全等三角形的对应边、对应角相等
22边角边公理(sas)有两边和它们的夹角对应相等的两个三角形全等
23角边角公理(asa)有两角和它们的夹边对应相等的两个三角形全等
24推论(aas)有两角和其中一角的对边对应相等的两个三角形全等
25边边边公理(sss)有三边对应相等的两个三角形全等
26斜边、直角边公理(hl)有斜边和一条直角边对应相等的两个直角三角形全等
27定理1在角的平分线上的点到这个角的两边的距离相等
28定理2到一个角的两边的距离相同的点,在这个角的平分线上
29角的平分线是到角的两边距离相等的所有点的集合
30等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角)
31推论1等腰三角形顶角的平分线平分底边并且垂直于底边
32等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合
33推论3等边三角形的各角都相等,并且每一个角都等于60°
希望上面的公式总结对大家的学习有所帮助。
三 : 高二数学公式总结之向量公式
四 : 高等数学公式总结
本文标题:高中数学公式总结-大学数学公式总结大全61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1