一 : 小学四年级奥数题及答案

小学四年级奥数题及答案

1、甲、乙两人相距10千米，甲在前，乙在后，甲每小时行5千米，乙每小时行6千米。两人同时出发同向而行，乙几小时能追上甲？

2、书架上放有3本不同的数学书，5本不同的语文书，6本不同的英语书。

（1）若从这些书中任取一本，有多少种不同的取法？

（2）若从这些书中取数学书、语文书、英语书各一本，有多少种不同的取法？

（3）若从这些书中取不同的科目两本，有多少种不同的取法？

3、学校进行篮球比赛， 上场时10名队员互相握了一次手，一共握了多少次手？

4、小林为家里做饭，他择菜要5分钟，淘米要2分钟，煮饭要15分钟，切菜花4分钟。如果只有单火头煤气灶，做完这些事情至少需要多少分钟？

5、24辆卡车一次能运货物192吨，同样的卡车36辆，一次能运货物多少吨？

6、张师傅计划加工552个零件，前五天加工345个，照这样计算，这批零件还要几天加工完？

7、修一条长1944米的 水渠，54人12天修好。若增加18人，天数缩小到原来的一半，可以修水渠多少米？

1、[解答]10/(6-5)=10(小时)

答：乙10小时能追上甲

2[解答]（1）3+5+6=14（种）答。。。

（2）3*5*6=90（种）

（3）3*5+3*6+5*6=63（种）

3【解答】9+8+7+6+5+4+3+2+1=45

4【解答】小林先淘米2分钟，接着煮饭15分钟，在煮饭的同时，可以择菜8分钟，洗菜5分钟，接着用2分钟切完菜花，取下饭后再用2分钟切菜花，最后炒菜用时6分钟。一共2+15+2+6=25（分钟） 5【解答】一份量：192/24=8（吨），

总数量：8*36=288（吨），

综合算式：192/24*36=288（吨）

6【解答】552-345=207（个）

345/5=69（个/天）

207/69=3（天）答：------

7【解答】1944/54/12=3米/（人*天）

54+18=72（人）

12/2=6（天）

3*72*6=1296（米）

二 : 第十届中环杯四年级决赛试题及答案

2010年3月20日第十届“中环杯”小学生思维能力训练活动

四年级决赛

一、填空题：（每题5分，共50分。）

1、 自然数1，2，3，……，1010的所有数码之和是_______。

2、 在200~300之间，有三个连续的自然数，其中最小的数是3的倍数，中间的数有约数5，最大的数能被7整除，这三个数的和是_______。

3、 今年世博会将于5月1日开始，10月31日结束。将这几个数字连接起来构成一串数字：05011031。紧接05011031后面写一串数字，写下的每一个数字都是它前面两个数字乘积的个位数，例如3?1?3，在1的后面写3；1?3?3，在3的后面写3；3?3?9，在3后面写9；3?9?27，在9的后面写7……这样得到一串数字为050110313397……。世博会一共持续184天，问这串数字从0开始往右数，第184个数字是_______。

4、 四位数1234可通过下面的变换变成1541：

12?1?21234????1541 34?3?4

现在有一个四位数，通过以上方法变换成3779，那么原来的这个四位数是_______。

5、 四⑴班共有47人，要从甲、乙、丙三人中投票选举出一人担任班长。已知每个人都投了一票给三人中的一人，并且在计票过程中的某一时刻，甲得到15票，乙得到13票，丙得到8票。如果得票数比其他两人都多的候选人将成为班长，那么甲最少再得_______票就能够保证当选。

6、 四年级同学春游时租船游湖。如果每条船坐14人，有一条船上多2个座位没人坐；如果每条船多坐4人，可以少租一条船，这时每人可节省1元。租一条船需要_______元。

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

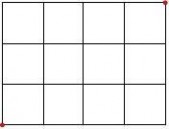
7、 灰太狼住在A处，它收到消息，喜洋洋现在在B处睡觉。图中的横线和竖线均表示道路，横线和竖线的交点表示道路的交叉处。灰太狼只能沿着道路走，若他要在最短的时间里抓到喜洋洋，则他共有_______种不同的走法。

8、 图书馆的阅览室里有若干张3条腿的凳子和4条腿的椅子，且每张凳子和椅子上都坐着一个人，每个人有2条腿。小红数了一下，阅览室里凳子的腿、椅子的腿和人的腿的总数为44，那么有_______张凳子，_______张椅子，_______个人。

9、 亮亮骑着自行车，以每分钟400米的速度，从46路汽车的始发站出发，沿46路车的线路前进。当他骑出1400米时，一辆46路车从始发站开出。已知这辆车每分钟行600米，每4分钟到达一站并停车1分钟。那么汽车开出_______分钟后能追上亮亮。

10、 如图，ABCD是边长为18厘米的正方形，M、N分别为AB边与BC边上的点，AM:MB?CN:NB?2:1，AN与CM相交于点O。四边形AOCD的面积是_______平方厘米。

DC

ON

AMB

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

二、动手动脑题：（每题10分，共50分。）

1、 能否用7个图1所示的卡片拼成一个图2所示的图形？如果能，请画出拼法；如果不能，请说明理由。

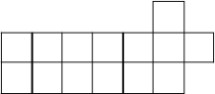
图1图2

2、 一个两位数，加上45以后，十位数字正好与个位数字互换位置。原来的这个两位数是多少？请写出所有可能。

3、 一块长方形铁皮，长130厘米，宽90厘米。现在要把这块铁皮制成一个深为10厘米的无盖长方体铁盒（焊接处与铁皮厚度忽略不计），求这个长方体铁盒的容积最大是多少立方厘米？并请你画出铁皮的分割方法，标上数据。

4、 一个小孩在沙滩上把16个贝壳分成8个，3个，5个共三堆。按照下面的规则进行移动：取其中的任意两堆贝壳，记为1号堆和2号堆，且1号堆的贝壳不少于2号堆，然后从1号堆拿取与2号堆相同数量的贝壳，放入2号堆。经若干次这样的移动，使所有的贝壳成为一堆。以下是一种移动方法：（8，3，5）?（8，6，2）?（8，4，4）?（8，8，0）?（16，0，0），共移动了4次。现在把16个贝壳分成9个，5个，2个共三堆，那么按照上面的规则，最少移动多少次，就能使所有的贝壳成为一堆？请写出移动过程。

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

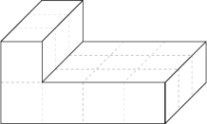
5、 图一中编号①~④的立体图形，分别是由3个或4个棱长为1的小正方体组成的，请你按照提供给你的卡纸上的折叠方法，制作出这4个几何体，并将它们拼成如图二的立体图形。每个几何体必须且只能用一次，可翻转拼搭。请在图二上用粗线条画出你的拼法，并标上每个几何体的编号。

①

②

③

图一④

图二

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

2010年3月20日第十届“中环杯”小学生思维能力训练活动

四年级决赛

一、填空题：（每题5分，共50分。）

1、 自然数1，2，3，……，1010的所有数码之和是_______。

【分析与解】

（方法一）

因为000~999的所有的数码和为?0?1?2?3?4?5?6?7?8?9???100?3??13500；

又因为0的数码为0，1000的数码之和为1?0?0?0?1，1001的数码之和为1?0?0?1?2， 1002的数码之和为1?0?0?2?3，1003的数码之和为1?0?0?3?4，1004的数码之和为1?0?0?4?5， 1005的数码之和为1?0?0?5?6，1006的数码之和为1?0?0?6?7，1007的数码之和为1?0?0?7?8， 1008的数码之和为1?0?0?8?9，1009的数码之和为1?0?0?9?10，1010的数码之和为1?0?1?0?2； 所以自然数1，2，3，……，1010的所有数码之和是

13500?0??1?2?3?4?5?6?7?8?9?10?2??13557。

（方法二）

因为?0?999???1?998?????499?500?在运算中未产生进位；

所以以上各数数码和就是自然数0，1，2，3，……，999的所有数码和；

所以自然数0，1，2，3，……，999的所有数码之和是?9?9?9??500?13500；

因为?1000?1009???1001?1008?????1004?1005?在运算中未产生进位；

所以以上各数数码和就是自然数1000，1001，……，1009的所有数码和；

所以自然数1000，1001，……，1009的所有数码之和是?2?0?0?9??5?55；

又因为0的数码为0，1010的数码之和为1?0?1?0?2；

所以自然数1，2，3，……，1010的所有数码之和是13500?55?0?2?13557。

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

2、 在200~300之间，有三个连续的自然数，其中最小的数是3的倍数，中间的数有约数5，最大的数能被7整除，这三个数的和是_______。

【分析与解】

?3,5,7??3?5?7?105；

105?3?108是3的倍数；

105?5?110有约数5；

105?7?112能被7整除；

故三个连续的自然数，满足最小的数是3的倍数，中间的数有约数5，最大的数能被7整除，

其中最小的一组是108?2?54，110?2?55，112?2?56；

又因为这三个在200~300之间；

所以这三个数是54?105?2?264，55?105?2?265，56?105?2?266；

这三个数的和是264?265?266?795。

3、 今年世博会将于5月1日开始，10月31日结束。将这几个数字连接起来构成一串数字：05011031。紧接05011031后面写一串数字，写下的每一个数字都是它前面两个数字乘积的个位数，例如3?1?3，在1的后面写3；1?3?3，在3的后面写3；3?3?9，在3后面写9；3?9?27，在9的后面写7……这样得到一串数字为050110313397……。世博会一共持续184天，问这串数字从0开始往右数，第184个数字是_______。

【分析与解】

因为紧接05011031后面写一串数字，写下的每一个数字都是它前面两个数字乘积的个位数；

所以从第1个3开始出现连续2个数相同，即可判断出周期性变化规律；

05011031339731??；

从第1个3开始出现周期性变化规律，以“313397”循环；

第1个3之前有050110这6个数字；

?184?6??6?29??4；

故第184个数字与“313397”中第4个数字相同，是3。

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

4、 四位数1234可通过下面的变换变成1541：

12?1?21234????1541 34?3?4

现在有一个四位数，通过以上方法变换成3779，那么原来的这个四位数是_______。

【分析与解】 设原来的四位数是abcd； 则变换后新的四位数前两位是ab?a?b，后两位是cd?c?d；

?a?3ab?a?b??10a?b??a?b?11a?2b?37；解得?； ?b2??c?7cd?c?d??10c?d??c?d?11c?2d?79；解得?； ?d?1

故abcd?3271，即原来的这个四位数是3271。

5、 四⑴班共有47人，要从甲、乙、丙三人中投票选举出一人担任班长。已知每个人都投了一票给三人中的一人，并且在计票过程中的某一时刻，甲得到15票，乙得到13票，丙得到8票。如果得票数比其他两人都多的候选人将成为班长，那么甲最少再得_______票就能够保证当选。

【分析与解】

现在还剩下47?15?13?8?11张选票没有统计。

如果甲再得4张，乙再得7张，则乙当选为班长；

如果甲再得5张选票，则无论剩余6张选票投给谁，甲必定当选为班长；

所以甲最少再得5票就能够保证当选。

6、 四年级同学春游时租船游湖。如果每条船坐14人，有一条船上多2个座位没人坐；如果每条船多坐4人，可以少租一条船，这时每人可节省1元。租一条船需要_______元。

【分析与解】

如果每条船坐14人，有一条船上多2个座位没人坐，即少2人；

如果每条船多坐4人，即每条船坐14?4?18人，可以少租一条船，即少18人；

原来准备租?18?2??4?4条船；

四年级同学一共有14?4?2?54或18??4?1??54人；

每人节省1元，则四年级同学一共节省1?54?54元；

所有四年级同学节省下来的钱相当于租一条船的费用；故租一条船需要54元。

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

7、 灰太狼住在A处，它收到消息，喜洋洋现在在B处睡觉。图中的横线和竖线均表示道路，横线和竖线的交点表示道路的交叉处。灰太狼只能沿着道路走，若他要在最短的时间里抓到喜洋洋，则他共有_______种不同的走法。

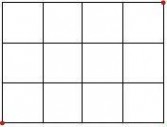
【分析与解】

（方法一）

灰太狼要在最短的时间里抓到喜洋洋；

则灰太狼从A处到B处要走最短路线；

故只能向右或者向上走；

从A处走到某个点的最短路线的条数

?其左边一个点的最短路线的条数?其下边一个点的最短路线的条数；

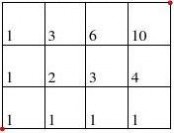
B

由标数法，灰太狼要在最短的时间里抓到喜洋洋，则他共有35种不同的走法。 （方法二）

灰太狼要在最短的时间里抓到喜洋洋；

则灰太狼从A处到B处要走最短路线；

故只能向右或者向上走；

无论哪一种走法都需要走过4步向右和3步向上；

那么可以从4?3?7个步骤中，任选4个向右，而其它均向上；或者任选3个向上，而其它均向右； 灰太狼要在最短的时间里抓到喜洋洋，则他共有C74?7?6?5?47?6?53?35或C7??35种不同的走法。 4?3?2?13?2?1

【说明】题目中“喜洋洋”正确的写法是“喜羊羊”。

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

8、 图书馆的阅览室里有若干张3条腿的凳子和4条腿的椅子，且每张凳子和椅子上都坐着一个人，每个人有2条腿。小红数了一下，阅览室里凳子的腿、椅子的腿和人的腿的总数为44，那么有_______张凳子，_______张椅子，_______个人。

【分析与解】

设有x张凳子，y张椅子，则有?x?y?个人；

?x?4由题意，得3x?4y?2?x?y??44，5x?6y?44，自然数解为?； ?y4?

故有4张凳子，4张椅子，4?4?8个人。

9、 亮亮骑着自行车，以每分钟400米的速度，从46路汽车的始发站出发，沿46路车的线路前进。当他骑出1400米时，一辆46路车从始发站开出。已知这辆车每分钟行600米，每4分钟到达一站并停车1分钟。那么汽车开出_______分钟后能追上亮亮。

【分析与解】

汽车开出4分钟后，亮亮和汽车相距1400??600?400??4?600分钟；

之后每5分钟，汽车先停1分钟，再行驶4分钟，汽车追近亮亮600?4?400?5?400米；

600?400?1??200；

即汽车开出4分钟后，再过5分钟，汽车和亮亮相距200米；

汽车第2次停车1分钟后，汽车和亮亮相距200?400?1?600米；

汽车第2次停车后行驶600??600?400??3分钟追上亮亮；

故汽车开出4?5?1?3?13分钟后能追上亮亮。

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

10、 如图，ABCD是边长为18厘米的正方形，M、N分别为AB边与BC边上的点，AM:MB?CN:NB?2:1，AN与CM相交于点O。四边形AOCD的面积是_______平方厘米。 D

C

O

N

AMB

【分析与解】 D

C

O

N

AMB

连接OB；

因为正方形ABCD中，AB?CB；又因为AM:MB?CN:NB?2:1；

所以由对称性可得S?ABN?S?CBM，S?BOM?S?BON，S?AOM?S?CON，S?AOB?S?COB； 因为AM:MB?2:1；所以S?AOM:S?BOM?2:1；所以S?AOM:S?BOM:S?BON?2:1:1； 因为S?ABN?AB?BN?2?AB??BC?3??2?18??18?3??2?54平方厘米；

所以S?BOM?S?ABN?4?54?4?13.5平方厘米，S?AOM?S?ABN?4?2?54?4?2?27平方厘米； 所以S?AOB?S?AOM?S?BOM?27?13.5?40.5平方厘米；所以S?COB?S?AOB?40.5平方厘米； 因为Ssquare

ABCD

?asquare

AOCD

2ABCD

?182?324平方厘米；

?S?COB?S?AOB?324?40.5?40.5?243平方厘米。

第十届“中环杯”小学生思维能力训练活动

四年级决赛

所以Squadrilateral?Ssquare

ABCD

城隍喵

二、动手动脑题：（每题10分，共50分。）

1、 能否用7个图1所示的卡片拼成一个图2所示的图形？如果能，请画出拼法；如果不能，请说明理由。

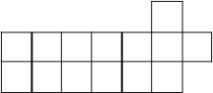
图1图2

【分析与解】

将图2中的这14

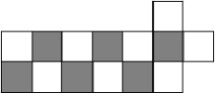
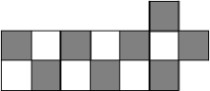
个小方格黑、白相间染色；

图3图4

如图3所示，有6个黑格，8个白格（或如图4所示，有6个白格，8个黑格）； 黑格与白格的数量不相等；

而相邻两个方格必然是一黑一白；

如果用7个图1所示的卡片拼成一个图2所示的图形，那么14个格应当是黑、白各7个； 所以不能用7个图1所示的卡片拼成一个图2所示的图形。

2、 一个两位数，加上45以后，十位数字正好与个位数字互换位置。原来的这个两位数是多少？请写出所有可能。

【分析与解】 设这个两位数是ab；

由题意，得ab?45?ba，?10a?b??45?10b?a，9b?9a?45，9?b?a??45，b?a?5；

?a?1?a?2?a?3?a?4

或?或?或?； 小于10的正整数解为?

??b?6b?7b8b9????所以这个两位数是16或27或38或49。

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

3、 一块长方形铁皮，长130厘米，宽90厘米。现在要把这块铁皮制成一个深为10厘米的无盖长方体铁盒（焊接处与铁皮厚度忽略不计），求这个长方体铁盒的容积最大是多少立方厘米？并请你画出铁皮的分割方法，标上数据。

【分析与解】

设这个长方体铁盒的长为a厘米，宽为b厘米；

a?b????a?b??2???10?130?90，

a?b?20a?20b?11700，

当V?a?b?10?10ab一定时，底面S底?a?b也为定值；

铁皮所用的面积为a?b????a?b??2???10?a?b??a?b??20；

面积一定长方形中，正方形的周长最小；

故当a?b时，铁皮所用的面积a?b????a?b??2???10?a?b??a?b??20最小；

反之，要使容积V?a?b?10?10ab达到最大时，a?b；

a?b?20a?20b?a?a?20a?20a?a??a?40??11700；

经尝试，当a?90时，a??a?40??90??90?40??11700；

故当a?b?90时，Vmax?10ab?10?90?90?81000；

这个长方体铁盒的容积最大是81000立方厘米； 铁皮的分割方法如图所示。

9010101010

90

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

4、 一个小孩在沙滩上把16个贝壳分成8个，3个，5个共三堆。按照下面的规则进行移动：取其中的任意两堆贝壳，记为1号堆和2号堆，且1号堆的贝壳不少于2号堆，然后从1号堆拿取与2号堆相同数量的贝壳，放入2号堆。经若干次这样的移动，使所有的贝壳成为一堆。以下是一种移动方法：（8，3，5）?（8，6，2）?（8，4，4）?（8，8，0）?（16，0，0），共移动了4次。现在把16个贝壳分成9个，5个，2个共三堆，那么按照上面的规则，最少移动多少次，就能使所有的贝壳成为一堆？请写出移动过程。

【分析与解】

采用倒推法。

最后一步是（16，0，0）；

倒数第二步必定是（8，8，0）；

倒数第三步是（12，4，0）或（8，4，4）；

倒数第四步是（14，2，0）或（12，2，2）或（10，6，0）

或（6，6，4）或（10，4，2）或（8，6，2）；

发现（9，5，2）可以变成（10，4，2）；

所以至少要移动4次，移动方法如下：

（9，5，2）?（10，4，2）?（8，4，4）?（8，8，0）?（16，0，0）

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

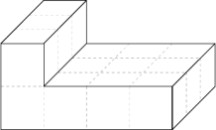
5、 图一中编号①~④的立体图形，分别是由3个或4个棱长为1的小正方体组成的，请你按照提供给你的卡纸上的折叠方法，制作出这4个几何体，并将它们拼成如图二的立体图形。每个几何体必须且只能用一次，可翻转拼搭。请在图二上用粗线条画出你的拼法，并标上每个几何体的编号。

①

②

③

图一④

图二

【分析与解】

答案如图三所示；答案不惟一。

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

④

图三

第十届“中环杯”小学生思维能力训练活动

四年级决赛

城隍喵

三 : 小学三年级奥数题及答案

小学三年级奥数题及答案

1.一条路长100米，从头到尾每隔10米栽1棵梧桐树，共栽多少棵树？ 路分成100÷10＝10段，共栽树10+1＝11棵。［www.61k.com］

12棵柳树排成一排，在每两棵柳树中间种3棵桃树，共种多少棵桃树？ 3×（12－1）＝33棵。

一根200厘米长的木条，要锯成10厘米长的小段，需要锯几次？ 200÷10＝20段，20－1＝19次。

4.蚂蚁爬树枝，每上一节需要10秒钟，从第一节爬到第13节需要多少分钟？

从第一节到第13节需10×（13－1）＝120秒，120÷60＝2分。

5.在花圃的周围方式菊花，每隔1米放1盆花。花圃周围共20米长。需放多少盆菊花？ 20÷1×1＝20盆

6.从发电厂到闹市区一共有250根电线杆，每相邻两根电线杆之间是30米。从发电厂到闹市区有多远？

30×（250－1）＝7470米。

7.王老师把月收入的一半又20元留做生活费，又把剩余钱的一半又50元储蓄起来，这时还剩40元给孩子交学费书本费。他这个月收入多少元？

[(40+50) ×2+20] ×2=400(元)答：他这个月收入400元。

8.一个人沿着大提走了全长的一半后，又走了剩下的一半，还剩下1千米，问：大提全长多少千米？

1×2×2＝4千米

9.甲在加工一批零件，第一天加工了这堆零件的一半又10个，第二天又加工了剩下的一半又10个，还剩下25个没有加工。问：这批零件有多少个？

（25+10）×2＝70个，（70+10）×2＝160个。综合算式：【（25+10）×2+10】×2＝160个

10.一条毛毛虫由幼虫长到成虫，每天长一倍，16天能长到16厘米。问它几天可以长到4厘米？ 16÷2÷2＝4（厘米），16-1-1＝14（天）

11.一桶水，第一次倒出一半，然后倒回桶里30千克，第二次倒出桶中剩下水的一半，第三次倒出180千克，桶中还剩下80千克。桶里原来有水多少千克？ 180+80＝260（千克），260×2-30＝490（千克），490×2＝980（千克）。

12.甲、乙两书架共有图书200本，甲书架的图书数比乙书架的3倍少16本。甲、乙两书架上各有图书多少本？ 答案：乙：（200+16）÷（3+1）=54（本）；甲：54×3-16=146（本）。

13.小燕买一套衣服用去185元，问上衣和裤子各多少元？

裤子：（185-5）÷（2+1）=60（元）； 上衣：60×2+5=125（元）。

14.甲、乙、丙三人年龄之和是94岁，且甲的2倍比丙多5岁，乙2倍比丙多19岁，问：甲、乙、丙三人各多大？

如果每个人的年龄都扩大到2倍，那么三人年龄的和是94×2=188。如果甲再减少5岁，乙再减少19岁，那么三人的年龄的和是188-5-19=164（岁），这时甲的年龄是丙的一半，即丙的年龄是甲的两倍。同样，这时丙的年龄也是乙两倍。所以这时甲、乙的年龄都是164÷（1+1+2）=41（岁），即原来丙的年龄是41岁。甲原来的年龄是（41+5）÷2=23（岁），乙原来的年龄是（41+19）÷2=30（岁）。

15.小明、小华捉完鱼。小明说：“如果你把你捉的鱼给我1条，我的鱼就是你的2倍。如果我给你1条，咱们就一样多了。“请算出两个各捉了多少条鱼。

小明比小华多1×2=2（条）。如果小华给小明1条鱼，那么小明比小华多2+1×2=4（条），这时小华有鱼4÷（2-1）=4（条）。原来小华有鱼4+1=5（条），原来小明有鱼5+2=7（条）。

小学三年级数学题 小学三年级奥数题及答案

16.小芳去文具店买了13本语文书，8本算术书，共用去10元。(www.61k.com)已知6本语文本的价钱与4本算术本的价钱相等。问：1本语文本、1本算术本各多少钱？ 8÷4×6=12，即8本算术本与12本语文体价钱相等。所以1本语文本值10×100÷（13+12）=40（分），1本算术本值40×6÷4=60（分），即1本语文本4角，1本算术本6角。

17.找规律，在括号内填入适当的数. 75，3，74，3，73，3，（），（）。 答案：72，3。

18找规律，在括号内填入适当的数. 1，4，5，4，9，4，（），（）。

奇数项构成数列1，5，9……，每一项比前一项多4；偶数项都是4，所以应填13，4

19.找规律，在括号内填入适当的数. 3，2，6，2，12，2，（），（）。 24，2。

20.找规律，在括号内填入适当的数. 76，2，75，3，74，4，（），（）。

答案：将原数列拆分成两列，应填：73，5。

21.找规律，在括号内填入适当的数. 2，3，4，5，8，7，（），（）。

答案：将原数列拆分成两列，应填：16，9。

22.找规律，在括号内填入适当的数. 3，6，8，16，18，（），（）。

答案：6＝3×2，16＝8×2，即偶数项是它前面的奇数项的2倍；又8＝6＋2，18＝16＋2，即从第三项起，奇数项比它前面的偶数项多2.所以应填：36，38。

23.找规律，在括号内填入适当的数. 1，6，7，12，13，18，19，（），（）。

答案：将原数列拆分成两列，应填：24，25。

24.找规律，在括号内填入适当的数. 1，4，3，8，5，12，7，（）。

答案：奇数项构成数列1，3，5，7，…，每一项比前一项多2；偶数项构成数列4，8，12，…，每一项比前一项多4，所以应填：16。

25.找规律，在括号内填入适当的数. 0，1，3，8，21，55，（），（）。 答案：144，377。

26.A、B、C、D四人在一场比赛中得了前4名。已知D的名次不是最高，但它比B、C都高，而C的名次也不比B高。问：他们各是第几名？ 答案：D名次不是最高，但比B、C高，所以它是第2名，A是第1名。C的名次不比B高，所以B是第3名，C是第4名。

27.一头象的重量等于4头牛的重量，一头牛的重量等于3匹小马的重量，一匹小马的重量等于3头小猪的重量。问：一头象的重量等于几头小猪的重量？

答案：4×3×3=36，所以一头象的重量等于36头小猪的重量。

28.甲、乙、丙三人，一个人喜欢看足球，一个人喜欢看拳击，一个人喜欢看篮球。已知甲不爱看篮球，丙既不喜欢看篮球又不喜欢看足球。现有足球、拳击、篮球比赛的入场券各一张。请根据他们的爱好，把票分给他们。

答案：丙不喜欢看篮球与足球，应将拳击入场券给丙。甲不喜欢看篮球，应将足球入场券给甲。最后，应将篮球入场券给乙。

29.有一堆铁块和铜块，每块铁块重量完全一样，每块铜块的重量也完全一样。3块铁快和5块铜块共重210克。4块铁块和10块铜块共重380克。问：每一块铁块、每一块铜块各重多少？ 答案：4块铁块和10块铜块共重380克，所以2块铁块和5块铜块共重380÷2=190（克）。而3块铁块和5块铜块共重210克，所以1块铁块重210-190=20（克）。1铜块重（190-20×2）÷5=30（克）。

30.甲、乙、丙三人中有一人做了一件好事。他们各自都说了一句话，而其中只有一句是真的。甲说：“是乙做的。” 乙说：“不是我做的。” 丙说：“也不是我做的。” 问：到底是谁做的好事？ 答案：如果是甲做的好事，那么乙、丙的话都是真的，与只有一句是真的矛盾。如果是乙做的好事，那么甲、丙的话都是真的，也产生矛盾。好

小学三年级数学题 小学三年级奥数题及答案

事是丙做的，这时甲、丙的话都是错的，只有乙的话是真的，所以好事是丙做的。[www.61k.com］

31.一张长8分米、宽3分米的长方形纸板，在四个角落上各截去一个边长为2分米的正方形，所剩下的部分的周长是多少？ 答：（8+3）×2=22（分米）

32.计算 ：18+19+20+21+22+23 原式=（18+23）×6÷2=123

33.计算 ：100+102+104+106+108+110+112+114

原式=(100+114) ×8÷2=856

34.995+996+997+998+999 原式=(995+999) ×5÷2=4985

35.：（1999+1997+1995+…+13+11）-（12+14+16+…+1996+1998）

第一个括号内的项数为（1999-11）÷2+1=995，所以原式=(1999-1998)+(1997-1996)+…+（13-12）+11=1×994+11=1005

三年级奥数

1、40个梨分给3个班，分给一班20个，其余平均分给二班和三班，二班分到( )个。

2、7年前，***年龄是儿子的6倍，儿子今年12岁，妈妈今年( )岁。

3、同学们进行广播操比赛，全班正好排成相等的6行。小红排在第二行，从头数，她站在第5个位置，从后数她站在第3个位置，这个班共有( )人

4、有一串彩珠，按“2红3绿4黄”的顺序依次排列。第600颗是( )颜色。

5、用一根绳子绕树三圈余30厘米，如果绕树四圈则差40厘米，树的周长有( )厘米，绳子长( )厘米。

6、一只蜗牛在12米深的井底向上爬，每小时爬上3米后要滑下2米，这只蜗牛要( )小时才能爬出井口。

7、锯一根10米长的木棒，每锯一段要2分钟。如果把这根木棒锯成相等的5段，一共要( )分钟。

8、3只猫3天吃了3只老鼠，照这样的效率，9只猫9天能吃( ) 只。

9、 ┖┴┴┴┴┴┴┴┴┴┚图中共有( )条线段。 10、 鸡兔共有23个头，有86只脚，那么鸡有（ ）只，兔有（ ）只。

二、应用题。(每小题5分，共50分)

1、文具店有600本练习本，卖出一些后，还剩4包，每包25本，卖出多少本？

2、三年级同学种树80颗，四、五年级种的棵树比三年级种的2倍多14棵，三个年级共种树多少棵？

3、学校有808个同学，分乘6辆汽车去春游，第一辆车已经接走了128人，如果其余5辆车乘的人数相同，最后一辆车乘了几个同学？

4、学校里组织兴趣小组，合唱队的人数是器乐队人数的3倍，舞蹈队的人数比器乐队少8人，舞蹈队有24人，合唱队有多少人？

5、小强在计算除法时，把除数76写成67，结果得到的商是15还余5。正确的商应该是几？

6、一个书架有3层书，共有270本，从第一层拿出20本放到第二层，从第三层拿出17本放到第二层，这时三层书架中书的本数相等，原来每层各有几本书？

小学三年级数学题 小学三年级奥数题及答案

7、箱里放着同样个数的铅笔盒，如果从每只里拿出60个，那么5只箱里剩下铅笔盒的个数的总和等于原来2只箱里个数的和。(www.61k.com)原来每只箱里有多少个铅笔盒？

8、参加四年级数学竞赛同学中，男同学获奖人数比女同学多2人，女同学获奖人数比男同学人数的一半多2人，男女同学各有多少人获奖？

9、两块同样长的布，第一块用去32米，第二块用去20米，结果所余的米数第二块是第一块的3倍。两块布原来各长多少米？

10、一个正方形，被分成5个相等的长方形，每个长方形的周长是60厘米，正方形的周长是多少厘米？

设原正方形边长5x，也就是长方形的长，则长方形的宽为x

得方程 2(5x+x)=60,

解得x=5厘米

所以正方形边长=5*5=25厘米，周长=4*25=100厘米

1、10 2、72 3、42 4、黄 5、70 6、8 7、8 8、27 9、19 10、3,20 应用题

1、600-25*4=500 2、设三年级共种x棵树 X+2x+14=80 X=22

3、（808-128）/ 5=136 4、（24+8）*3=64

5、（15*67+5）/76=13.。。。22 6、设第一层x本 （x+20+17）*3=270 X=53

第一层有73本 第二层有53本 第三层有70

7、5×60÷（5-2）=100（个） 8、设男同学获奖人数为x 则x=x/2+2+2 解之得 x=8

男同学8人获奖，女同学6人获奖。9、设第一块布为x米 3*（X-32 ）=x-20 2x=76 X=38 10、

本文标题：四年级奥数题及答案-小学四年级奥数题及答案
本文地址： http://www.61k.com/1074644.html