短时傅里叶变换-短时傅里叶变换：短时傅里叶变换-基本内容

发布时间：2017-11-15 所属栏目：信息与通信

一 : 短时傅里叶变换：短时傅里叶变换-基本内容

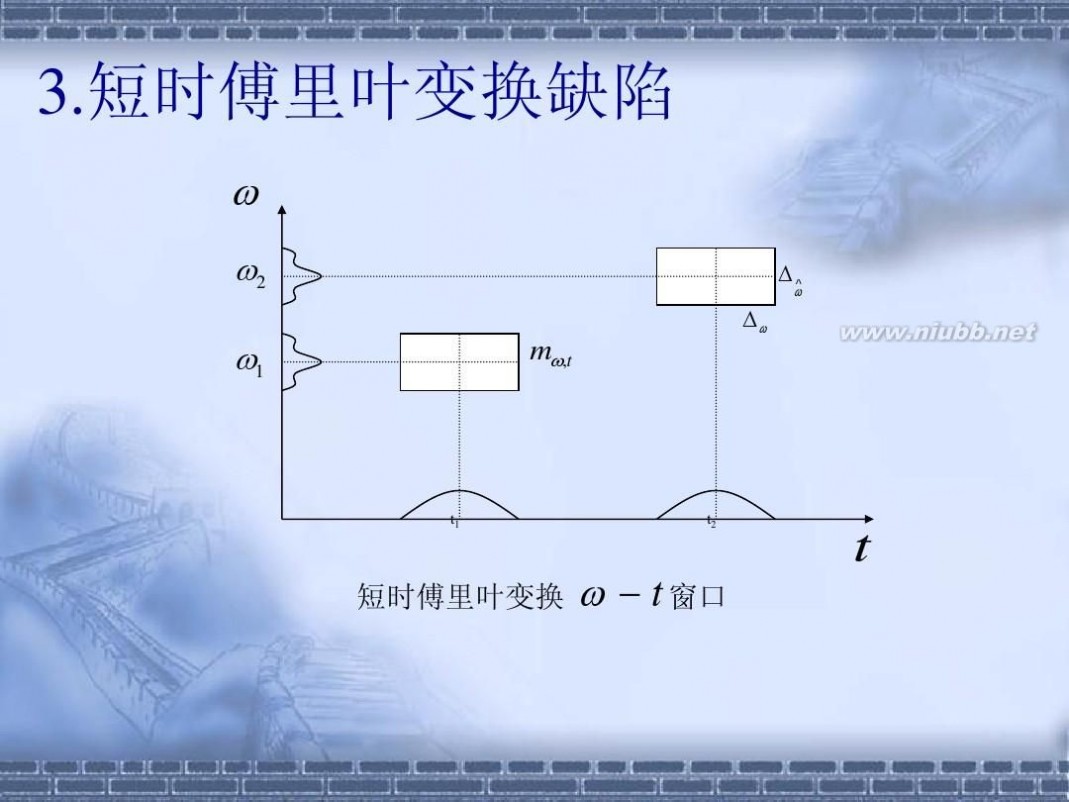
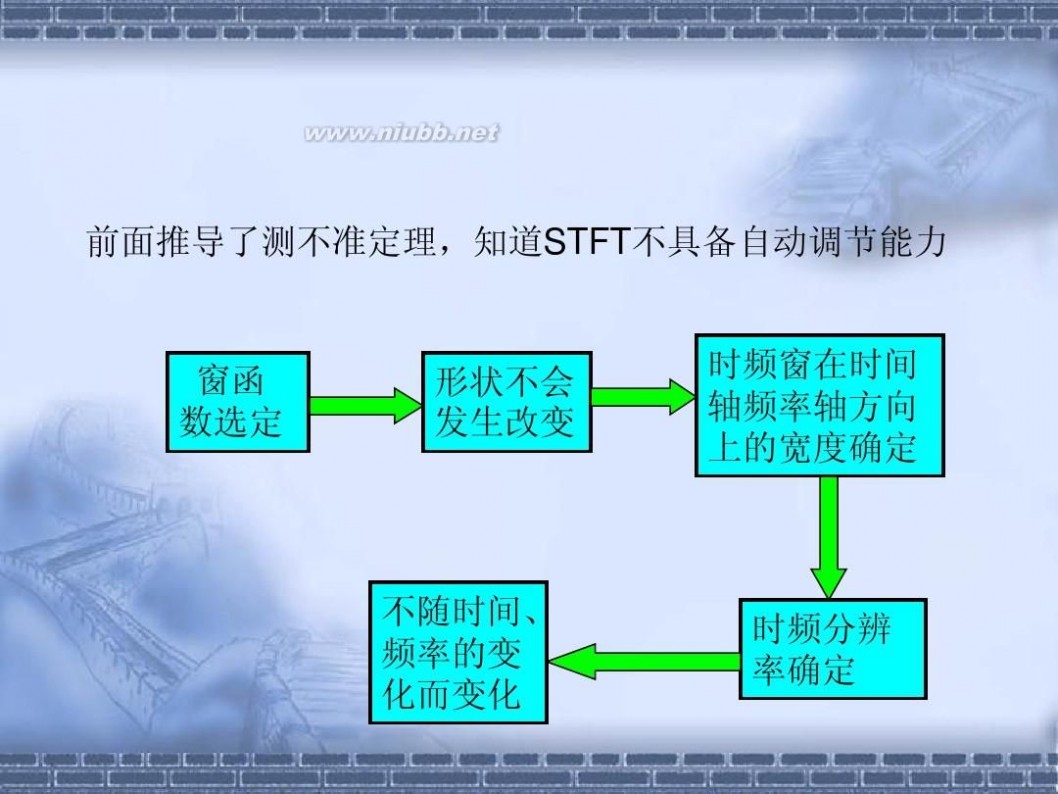
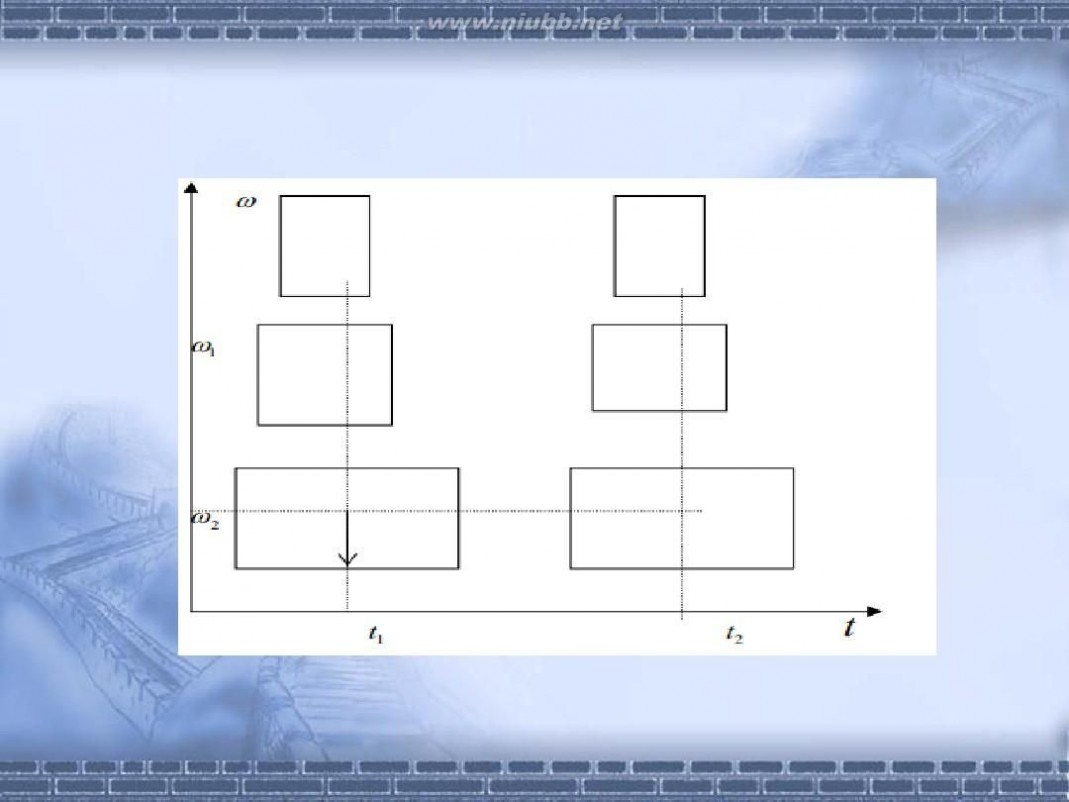
短时傅里叶变换（STFT，short-time Fourier transform，或 short-term Fourier transform)）是和傅里叶变换相关的一种数学变换，用以确定时变信号其局部区域正弦波的频率与相位。短时傅里叶变换用来分析分段平稳信号或者近似平稳信号犹可，但是对于非平稳信号，当信号变化剧烈时，要求窗函数有较高的时间分辨率;而波形变化比较平缓的时刻，主要是低频信号，则要求窗函数有较高的频率分辨率。短时傅里叶变换使用一个固定的窗函数，窗函数一旦确定了以后，其形状就不再发生改变，短时傅里叶变换的分辨率也就确定了。

短时傅里叶变换_短时傅里叶变换 -基本内容

[www.61k.com］短时傅里叶变换(STFT，short-time Fourier transform，或 short-term Fourier transform))是和傅里叶变换相关的1种数学变换，用以确定时变信号其局部区域正弦波的频率与相位。

它的思想是:选择1个时频局部化的窗函数，假定分析窗函数g(t)在1个短时间间隔内是平稳(伪平稳)的，移动窗函数，使f(t)g(t)在不同的有限时间宽度内是平稳信号，从而计算出各个不同时刻的功率谱。短时傅里叶变换使用1个固定的窗函数，窗函数一旦确定了以后，其形状就不再发生改变，短时傅里叶变换的分辨率也就确定了。如果要改变分辨率，则需要重新选择窗函数。短时傅里叶变换用来分析分段平稳信号或者近似平稳信号犹可，但是对于非平稳信号，当信号变化剧烈时，要求窗函数有较高的时间分辨率;而波形变化比较平缓的时刻，主要是低频信号，则要求窗函数有较高的频率分辨率。短时傅里叶变换不能兼顾频率与时间分辨率的需求。短时傅里叶变换窗函数受到W.Heisenberg不确定准则的限制，时频窗的面积不小于2。这也就从另1个侧面说明了短时傅里叶变换窗函数的时间与频率分辨率不能同时达到最优。

二 : STFT短时傅里叶变换08

4.1 短时傅立叶变换--概述

4.2.1 短时傅立叶变换--定义

? 定义：短时傅立叶变换也叫短时谱（加窗的方式）

X n (e ) ? ? x(m) w(n ? m)e ? j?m

j? m ? ??

? 短时谱的特点： 1)时变性：既是角频率ω 的函数又是时间n的函数 2)周期性：是关于ω 的周期函数，周期为2π

短时傅立叶变换主要用于语音分析合成系统，由其逆变换可以精确地恢复语音波形；

4.2.1 短时傅立叶变换--定义

? 短时傅里叶变换是窗选语音信号的标准傅里叶变换。下标n区别于标准的傅里叶变换。w(n-m)是窗口函数序列。不同的窗口函数序列，将得到不同的傅里叶变换的结果。 ? 短时傅里叶变换有两个自变量：n和ω，所以它既是关于时间n的离散函数，又是关于角频率ω的连续函数。 ? 与离散傅里叶变换和连续傅里叶变换的关系一样，若令 ω＝2πk/N，则得离散的短时傅里叶变换,它实际上是在频域的取样。

X n (e

2 k? N

) ? X n (k ) ?

m? ??

? x(m)w(n ? m)e

2 k?m N

0 ? k ? N ?1

4.2.1 短时傅立叶变换--定义

? 这两个公式都有两种解释：

? ① 当n固定不变时，它们是序列w(n-m)x(m) (-∞＜m＜∞)的标准傅里叶变换或标准的离散傅里叶变换。此时与标准傅里叶变换具有相同的性质，而Xn(k)与标准的离散傅里叶变换具有相同的特性。 ? ② 当ω或k固定时，和Xn(k)看做是时间n的函数。它们是信号序列和窗口函数序列的卷积，此时窗口的作用相当于一个滤波器。?

4.2.1 短时傅立叶变换--定义

? 频率分辨率Δf、取样周期T、加窗宽度N三者关系：

1 ?f ? NT

? 窗形状对短时傅立叶变换的影响－矩形窗——主瓣窄，衰减慢；－汉明窗——主瓣宽，衰减快； ? 窗宽对短时频谱的影响－窗宽长——频率分辨率高，能看到频谱快变化；－窗宽短——频率分辨率低，看不到频谱的快变化；

4.2.2 短时傅立叶变换--标准傅里叶变换的解释

? 短时傅里叶变换可写为?

X n (e j? ) ?

? ? 当n取不同值时窗w(n-m)沿着x(m)序列滑动，所以w(n-m)是一个“滑动的”窗口。 ? 由于窗口是有限长度的，满足绝对可和条件，所以这个变换是存在的。与序列的傅里叶变换相同，短时傅里叶变换随着ω作周期变化，周期为2π。

m ? ??

[ x(m)w(n ? m)]e ? j?m ?

4.2.2 短时傅立叶变换--标准傅里叶变换的解释

? 根据功率谱定义，可以写出短时功率谱与短时傅里叶变换之间的关系? S (e j? ) ? X (e j? ) ? X * n (e j? ) ?| X (e j? ) |2 n n n ? ? 式中*表示复共轭运算。同时功率谱是短时自相关函数? ? Rn (k ) ? ? w(n ?

m) x(m)w(n ? k ? m) x(m ? k ) ? 的傅里叶变换。? m??? ? 下面将短时傅里叶变换写为另一种形式。设信号序列和窗口序列的标准傅里叶变换为?

X (e ) ?

j? m ? ??

? x(m)e

? j?m

W (e ) ?

m ? ??

? w(m)e

? j?m

均存在。当n取固定值时，w(n-m)的傅里叶变换为?

m ? ??

? w(n ? m)e

? j?m

? e ? j?n ? W (e ? j? )

4.2.2 短时傅立叶变换--标准傅里叶变换的解释

? 根据傅里叶变换的频域卷积定理，有?

X n (e j? ) ? X (e j? ) *[e ? j?n ? W (e ? j? )]

4.2.2 短时傅立叶变换--标准傅里叶变换的解释

? 用波形乘以窗函数，不仅为了在窗口边缘两端不引起急剧变化，使波形缓慢降为零，而且还相当于对信号谱与窗函数的傅里叶变换进行卷积。 ? 为此窗函数应具有如下特性：?

? ① 频率分辨率高，即主瓣狭窄、尖锐；?（矩形窗） ? ② 通过卷积，在其他频率成分产生的频谱泄漏少，即旁瓣衰减大。?（海明窗） ? 这两个要求实际上相互矛盾，不能同时满足。?

? 窗口宽度N、取样周期T和频率分辨率Δf之间存在下列关系?Δf＝1/NT ? ? 可见：

? 窗口宽度↑→频率分辨率↑ 时间分辨率↓ ? 窗口宽度↓→频率分辨率↓ 时间分辨率↑，因而二者是矛盾的。?

4.2.2 短时傅立叶变换--标准傅里叶变换的解释

? 第一个零点位置为2π/N，显然它与窗口宽度成反比。

? 矩形窗，虽然频率分辨率很高，但由于第一旁瓣的衰减只有13.2dB，所以不适合用于频谱成分动态范围很宽的语音分析中。 ? 海明窗在频率范围中的分辨率较高，而且由于旁瓣的衰减大于42dB，具有频谱泄漏少的优点，频谱中高频分量弱、波动小，因而得到较平滑的谱。 ? 汉宁窗是高次旁瓣低，第一旁瓣衰减只有30dB。

? 对语音波形乘以海明窗，压缩了接近窗两端的部分波形，等效于用作分析的区间缩短40%左右，因此，频率分辨率下降40%左右。所以，即使在基音周期性明显的浊音频谱分析中，乘以合适的窗函数，也能抑制基音周期与分析区间的相对相位关系的变动影响，从而得到稳定的频谱。因为乘以窗函数将导致分帧区间缩短，所以为跟踪随时间变化的频谱，要求一部分区间重复移动。

4.2.2 短时傅立叶变换--标准傅里叶变换的解释

给出了N＝500时(取样率10 kHz，窗持续时间50 ms)时直角窗及海明窗下浊音语音的频谱。

? 其中图(a)是海明窗的窗选信号，图(b)是其对数功率谱；图 (c) 是矩形窗下的窗选信号，图(d) 是其对数功率谱。 ? 从图 (a)可以明显看出时间波形的周期性

，此周期性同样在图(b)中表现出来。图中基频及其谐波在频谱中表现为等频率间隔的窄峰。图(b)中的频谱大约在300～400Hz附近有较强的第一共振峰，而约在 2000Hz附近有一个对应于第二、三共振峰的宽峰。此外，还能在3 800Hz附近看到第四个共振峰。最后，由于声门脉冲谱的高频衰减特性，频谱在高频部分表现出下降的趋势。 ? 13

4.2.2 短时傅立叶变换--标准傅里叶变换的解释

? 将图(b)和图(d)比较可看出它们在基音谐波、共振峰结构以及频谱粗略形状上的相似性，同样也能看到其频谱之间的差别。 ? 最明显的是图(d)中基音谐波尖锐度增加，这主要是由于矩形窗频率分辨率较高。 ? 另一差别是矩形窗较高的旁瓣产生了一个类似于噪声的频谱。这是由于相邻谐波的旁瓣在谐波间隔内的相互作用(有时加强有时抵消)，因而在谐波间产生了随机变化。这种相邻谐波间不希望有的“泄漏”抵消了其主瓣较窄的优点， ? 因此在语音频谱分析中极少采用矩形窗。?

给出了N＝500时(取样率10 kHz，窗持续时间50 ms)时直角窗及海明窗下浊音语音的频谱。

4.2.2 短时傅立叶变换--标准傅里叶变换的解释

? 图4-3给出了N＝50的比较结果(取样率与图 4-2中相同，因而窗口持续时间为5ms)。 ? 由于窗口很短，因而时间序列(图(a)和(c))及信号频谱(图(b)和(d)) 均不能反映信号的周期性。 ? 与图4-2相反，图4-3只大约在400、1 400及2 200Hz频率上有少量较宽的峰值。它们与窗内语音段的前三个共振峰相对应。比较图4-3(b) 及(d)的频谱后，再次表明矩形窗可以得到较高的频率分辨率。?

4.2.2 短时傅立叶变换--标准傅里叶变换的解释

? 结论:

? 窗口宽度与短时傅里叶变换特性之间的关系 ? 用窄窗可得到好的时间分辨率 ? 用宽窗可以得到好的频率分辨率。 ? 但由于采用窗的目的是要限制分析的时间以使其中波形的特性没有显著变化，因而要折衷考虑。

4.2.3 短时傅立叶变换--滤波器的解释一

X n (e ) ?

? ? ? ?

w(n) ----------一个滤波器的单位函数响应 X n (e j? ) -----该滤波器的输出 x(n)------滤波器的输入过程:调制+滤波

m ? ??

?[ x(m)e

? j?m

]w(n ? m)

图4-4 短时傅里叶变换滤波器解释的第一种形式(a)复数运算

4.2.3 短时傅立叶变换--滤波器的解释二

X n (e ) ?| X n (e ) | e

j?n (? )

? an (?) ? jbn (?)

图4-4 短时傅里叶变换滤波器解释的第一种形式 (b)只有实数运算

4.2.3 短时傅立叶变换--滤波器的解释三

? 令m=n-m′

X n (e ) ?

j? m' ? ??

? w(m )x(n ? m )e

' '

? j? ( n ? m' )

? j?n

m' ? ??

? w(m '

)x(n ? m' )e j?m

令 : X n (e ) ?

m' ???

? w(m )x(n ? m )e

' '

j?m'

所以: X n (e ) ? e

? j?n

~ j? ? X n (e )

4.2.3 短时傅立叶变换--滤波器的解释

? 为窄带低通滤波器。第一种形式为低通滤波器； ? 由于第二种形式中的滤波器单位函数响应为 w(n)(e ) ，所以它为带通滤波器。

j?n

W (e j? )

4.2.3 短时傅立叶变换--滤波器的解释

~ 2 2 | X n (e j? ) |? [a n (? ) ? bn (? )]1 / 2 ?| X n (e j? ) | ? | e ? j?n | ~ ~ j? ~ 2 (? ) ? b 2 (? )]1 / 2 | X n (e ) |? [a n n

? 如果将w(n)的滤波运算除外，短时傅里叶变换实际上是对信号的幅度调制。

e ? j?n 相当于 ? 第一种形式是在输入端进行调制，x(n)乘以

将x(n)的频谱从ω移到零频处；而w(n)(直角窗或海明窗等)为窄带低通滤波器。 ? 后一种形式是在输出端进行调制，此时先对信号进行带通滤波，滤波器的单位函数响应为w(n) e ? j?n ,而调制后输出的是中心频率为ω的短时谱。?

4.3 短时傅立叶变换的取样率

恢复出x(n)的过程称为短时傅里叶反变换，是由短时谱合成语音信号的问题 X n (e j? )是n和ω的二维函数，因而必须对 ? 由于 X n (e j? ) 在所涉及的两个变量，即时域及频域内进行取样，取样率的选取应保证 X n (e j? ) 不产生混叠失真，从而能够恢复原始语音信号x(n)。

X n (e j? )

4.3 短时傅立叶变换的取样率---时间取样率

? 当ω为固定值时，是一个单位函数响应为w(n)的低通滤波器的输出。设低通滤波器的带宽为BHz，则 X (e ) 具有与窗相同的带宽。根据取样定理，X (e ) 的取样率至少为 2B才不致混叠。 ? 低通滤波器的带宽由w(n)的傅里叶变换W (e ) 的第一个零点位置ω01决定，因而B值取决于窗的形状与长度。 ?

X n (e j? )

j? n j? n

4.3 短时傅立叶变换的取样率---时间取样率

? 正弦序列的表达式为

f (k ) ? A sin(?0 k ? ? )

? 幅值A、初相φ的含义与模拟正弦信号相同 ? 正弦序列的数字角频率Ω0的含义与一般模拟信号模拟角频率ω0的概念不同。 ? 离散信号定义的时间为kT，显然有Ω0 =ω0 T，模拟角频率ω0的单位是rad/s， ? 数字角频Ω0的单位为rad/s · = rad。Ω0表示 s 相邻两个样值间弧度的变化量。

4.3 短时傅立叶变换的取样率---时间取样率

? 以直角窗和海明窗为例，其第一个零点位置分别为 2π ／N和4π／N ? 数字角频率与模拟频率F之间的关系为ω＝2πFT＝2πF ／fs(其中T是信号取样周期，fs是取样率)，因而用模拟频率表示的 W (的带宽为 e j? )

4.3 短时傅立叶变换的取样率---频率取样率

4.3 短时傅立叶变换的取样率---总取样率

4.4 语音信号的短时综合--滤波器组求和法

hk(n)是一个带通滤波器，其中心频率为ωk。yk(n)是第k个滤波器hk(n)的输出。

4.4 语音信号的短时综合--滤波器组求和法

L≥N时，y(n)正比于x(n)且与窗口w(n)的形状无关 L＜N时，通过合理地选取窗函数，也可以使y(n)得以精确地恢复。

4.4 语音信号的短时综合--滤波器组求和法

4.4 语音信号的短时综合--快速傅里叶变换求和法

4.5 语谱图

? 语音的时域分析和频域分析是语音分析的两种重要方法。

? 这两种方法均有局限性： ? 时域分析对语音信号的频率特性没有直观的了解； ? 频域特性中又没有语音信号随时间的变化关系。

? 时间依赖于傅里叶分析的显示图形称为语谱图。

? 语谱图中显示了大量的与语音的语句特性有关的信息，它综合了频谱图和时域波形的优点，明显地显示出语音频谱随时间的变化情况。

4.5 语谱图

? 语谱图实际上是一种动态的频谱。 ? 语谱图的纵轴为频率，横轴为时间。任一给定频率成分在给定时刻的强弱用点的黑白度来表示，频谱值大则记录得浓黑一些，反之则浅淡一些。? ? 用语谱图分析语音又称为语谱分析，记录语谱图的仪器就是语谱仪。 ? 语谱仪实际上是使一个带通滤滤器的中心频率发生连续变化，来进行语音的频率分析。 ? 带通滤波器有两种带宽：窄带为45 Hz，宽带为300 Hz。窄带语谱图有良好的频率分辨率及较差的时间分辨率；而宽带语谱图具有良好的时间分辨率及较差的频率分辨率。 ? 窄带语谱图中的时间座标方向表示的是基音及其各次谐波；而宽带语谱图给出语音的共振峰频率及清辅音的能量汇集区；这里，共振峰呈现为黑色的条纹。?

4.5 语谱图

? 所有元音的特征都是强度变化的规则的垂直条纹。

? 条纹的起点相当于声门脉冲的起点，条纹之间的距离表示基音周期。 ? 条纹越密表示基音频率越高，例如“Ten”中的［ε?］音；而基音周期在“the”字中［e］音时达到最大。 41

4.5 语谱图

? 声道的共振峰表示基音脉冲的某些频率成分被加强，这在语谱图上呈现为条纹区更宽更黑。 ? 摩擦音如［ｓ］、［ｚ］呈现不规则的条纹，主要在2.5 kHz 以上；这些条纹表示存

三 : 短时傅里叶变换STFT

短时傅里叶变换短时傅里叶变换STFT