一 : 云南最美自驾游路线推荐
云南历史 文化悠久,自然风光绚丽,去云南旅游,最适合就是自驾游,盘点云南十条超美自驾游线路,你喜欢哪一条。
自驾云南,你将欣赏到美丽神奇的自然风光,体验到绚丽多姿的民族风情,探索到源远流长的历史文化,感受到多元包容的宗教信仰;自驾云南,你的身心会全部融入到这片和谐、闲适的度假胜地,并找寻到心灵回归自然的乐园。
滇南线路
自驾线路一:昆明—建水—元阳—蒙自—屏边—河口—昆明(950公里)
沿途景点:朝阳楼、建水孔庙、燕子洞、双龙桥、指林寺、纳楼长官司署、朱家花园、小桂湖、观音山省级风景名胜区、元阳梯田、蒙自南湖、碧色寨景区、缘狮洞、龙宝洞、观音殿、大围山国家级自然保护区、河口
自驾时间:6天

自驾线路二:昆明—泸西—弥勒—昆明(360公里)
沿途景点:泸西阿庐古洞、歹鲁瀑布、九溪山休闲胜地、城子古村、南盘江峡谷风光、生态湖温泉、锦屏山
自驾时间:2天
自驾线路三:昆明—建水—开远—弥勒—昆明(590公里)
沿途景点:朝阳楼、建水孔庙、燕子洞、双龙桥、南洞风景区、泸江公园、热带植物园、灵芝湖、森林公园、生态湖温泉、锦屏山
自驾时间:2天
滇西路线
自驾线路四:昆明—武定—元谋人—永仁—大姚—姚安—南华—楚雄—昆明(570公里)
沿途景点:禄丰恐龙谷世界旅游区、楚雄紫溪山、彝族十月太阳历文化园、彝人古镇博物馆、咪依噜风情谷、三潭景区、永安方山、元谋土林、武定狮子山
自驾时间:3天
自驾线路五:昆明—楚雄—大理(云南驿)—保山—从隆阳区分线,沿滇缅公路到施甸、龙陵、德宏,沿史迪威公路北线到腾冲、缅甸密支那。
沿途景点:惠通桥、松山大战遗址、龙陵抗战纪念广场、国殇墓园、滇缅抗战博物馆、梁金山故居、光尊寺、李根源故居、密支那二战机场遗址
自驾时间:4天
自驾线路六:昆明—楚雄—巍山(324公里)
沿途景点:巍山古城、鸟道雄关、红河源、东莲花村、回族村落清真寺、群山龙山于图城遗址
自驾时间:2天
滇东北路线
自驾线路七:昆明—曲靖市—宣威市—会泽县(310公里)
沿途景点:江西会馆、大海草山风景区、会泽大地缝风景区、会泽古城、国家级大桥黑颈鹤自然保护区
自驾时间:1天
滇西南路线
自驾线路八:昆明—大理—潞江坝—和顺侨乡—土司署—盈江—瑞丽—芒市—怒江坝—大理—昆明(1800公里)
沿途景点:腾冲火山公园、叠水河瀑布、热海、北海湿地、和顺侨乡、艾思奇故居、和顺图书馆、和顺民居、文昌宫抗战博物馆、盈江允燕塔、苏典诗蜜瓦底风光、畹町中缅友谊桥、莫里热带雨林、中缅友谊街、宝石谷、姐告320国道纪念碑、天涯海角、仰光大金塔、云峰寺大佛、芒市树包塔
自驾时间:7天
自驾线路九:昆明—玉溪—玉元高速—213国道—思小高速—214国道—宣慰大道—西双版纳(760公里)
沿途景点:勐远仙境、望天树热带雨林景区、易武、磨憨
自驾时间:4天

滇东路线
自驾线路十:昆明—昆石高速—石林—西石高速—西桥—召夸—江召高速—师宗—英武山—凤凰谷—五龙
沿途景点 凤凰谷:典型的亚热带气候、喀斯特地型合力创造力一副天然的生命文化画卷。集峡谷、飞瀑、溶洞、湖泊、壮乡风情为一体,荟萃世界第一高洞、世界第一天然大佛、世界第一生命文化雕塑群,是国内首家生命文化主题风景区。
英武山:是集森林与喀斯特自然景观为一体的山岳型度假区。
壮乡五龙:全省60个旅游小镇之一,五条河流自东西南北在这里相聚,孕育了壮乡山水田园的风光。
自驾时间:4天
二 : 寻深圳回湖南邵阳的最佳路线,春节假期,自驾。。。
寻回湖南邵阳 的最佳路线,春节假期,自驾。。。
深圳到广州走广深高速--->广清高速----清连高速--宜凤高速--京珠高速--衡邵高速,这条不错,而且还挺快的。
三 : 云南自驾游最优路线设计
云南自驾游最优路线设计
摘要:大众旅游时代的到来,使旅游日益成为现代人类社会主要的生活方式和社会经济活动,旅游业以其强劲的势头成为全球经济产业中最具活力的“朝阳产业”。(www.61k.com)随着社会生产力不断发展,劳动生产率不断提高,以及人们生活水平的迅速提高和带薪假期的增加,旅游业将持续高速度发展,成为世界最重要的经济部门之一。
目前旅游业在我省得到了迅速健康的发展,并极大的促进了我省经济的发展。随着我国国民可支配收入和闲暇时间的增多,国内旅游需求日益扩大。这将为我省旅游业提供更大的发展空间。本文对云南几大著名旅游景区的消费等方面进行了讨论,在满足相关约束条件的情况下,设计线路最短、费用最低的旅游线路。基于对此的研究,建立数学模型(运用图论模型得出最短路程,再运用非线性规划软件进行求解),从而设计出最佳的旅游路线。
关键词:最短路线 最少费用 最优设计 lingo求解 决策变量
云南自驾游 云南自驾游最优路线设计
一、问题重述
云南是我国的旅游大省,拥有丰富的旅游资源,吸引了大批的省外游客,旅游业正在成为云南的支柱产业。(www.61k.com]随着越来越多的人选择到云南旅游,旅行社也推出了各种不同类型的旅行路线,使得公众面临多条线路的选择问题。
问题:某一个从没有到过云南的人准备在假期带家人到云南旅游,预计从昆明出发,并最终返回昆明。请你选择以下两种旅行方式之一为他设计一条在云南旅游的最佳路线(要有清晰的评价说明)。
1、旅行者采取自驾游的旅行方式。
2、旅行者可以根据不同情况自由选择交通方式,比如乘飞机、乘汽车、乘火车。
二、问题分析
时间允许的情况下,着重分析昆明、楚雄、大理、丽江、香格里拉、临沧、思茅、西双版纳、玉溪、曲靖几大旅游景区之间的距离,找出最短的旅游路线达到用时最短,花钱最少的目的,由此得出最佳的旅游路线。根据(附录1)可大致得出云南各旅游景区分布图的距离赋权图(如图1所示)。进而得出最短旅游路线,运用非线性规划求出用时最短,花钱最少的旅游路线即可。
把每个旅游景区看作是图1中的顶点vi,i=1,2,?,10,把每个旅游景区间的公路看成边,两景区间的距离看作边上的权值,则云南的 1
云南自驾游 云南自驾游最优路线设计
旅游路线图可看成是一个赋权图或网络。[www.61k.com)求最佳旅游路线就转化成了对应旅游路线图中的闭路径。此题为一推销员问题,可将其转化为求一赋权完全图的最优哈密尔顿回路问题。
三、模型假设
1)我们只考虑这10个旅游景区的情况,到达每个旅游景区可以游览全部的旅游景点,也可以不全部游览,但游览景点总数不少于20;
2)假设旅游者在云南旅游的时间最多不超过一个月,时间不允许情况下不超过10天;
3)假定油价7.5元/升,每升油可供汽车行驶20公里;
4)没有阴雨天气,汽车匀速行驶,且时速为80公里/小时;
5)旅游者每次都能正确到达下一旅游景区,没有迷路的情况;
6)路上没有车抛锚现象,且不计加油时间;
7)在考虑最短路线时,所截取的路线均是直线,不涉及实际路线要求;
8)到达每个旅游景区只游览一次,可重复经过同一条路线;
9)忽略景区内4个景点间的距离,即:不计景点间的交通费;
10)本文只考虑自驾的旅游路线。
2
云南自驾游 云南自驾游最优路线设计
四、符号说明
i,j——第i个或者第j个景点,i,j=1,2,??,10;
分别表示昆明、楚雄、大理、丽江、香格里拉、临沧、思茅、西双版纳、玉溪、曲靖;
vi,vj——网络中任意两个顶点;
jdij
vim
tij——vi到v的距离; ——第i个景区的第m个景点; ——表示从第i个景区到第j个景区路途中所需时间;
个景点的逗留时间; tim——表示旅游者在第i个景区的第m
ti——表示旅游者在第i个景区的逗留时间
c?k?——任一条旅游路线;
w——每个旅游者的旅游总花费;
wi——每个旅游者在第i个景区的总消费;
wim——每个旅游者在第i个景区的第m个景点的总费用;
wij——从第i个景点到第j个景点所需的交通费用; ?1旅游者到第i个景区的第m个景点旅游rim?其他?0
?1旅游者直接从第rij?? ?0; 。(www.61k.com] i个景点到达第其他j个景点
五、模型建立
方案一:消费最少路线。根据给定的时间约束,以费用最小为目 3
云南自驾游 云南自驾游最优路线设计
标,我们建立了一个最优规划模型。[www.61k.com)再根据引入的0—1变量表示是否游览某个景区,从而推出交通费用和景区花费的函数表达式,给出相应的约束条件,使用lingo编程对模型求解,得到最优规划。
游览的总费用由2部分组成,分别为交通总费用和在旅游景点的花费。我们定义:
w——每个旅游者的旅游总花费;
w?——每个旅游者在旅游景点的花费; w??——每个旅游者的交通总费用;
从而得到目标函数: Min w=w??+w? (1)旅游景区的总花费
w表示旅游者在i个景区和在第j个景区的总消费,w,因为wi,
j
im
wjm表示旅游者在第irim,rjm
个景区和在第j个景区的第m个景点的花费,
表示出旅游者是否去第i个景区和在第j个景区的第m个景点
的0—1变量,则
4
wi?
?w
m?1
imim
r
,wj
4
?
?w
m?1
jm
rjm
,
即旅游者在旅游景区的总花费为:
w??
12
10
?
?
i?1
?4
?rij???wimrim?j?1?m?1
104
?w
m?1
jm
?
rjm?
?
(2)交通总花费
由于w表示从第i个景区到第j个景区所需的交通费用,而r表示
ij
ij
旅游者是否从第i个景区直接到达第j个景区的0—1变量,因此可以得到交通总费用为:
4
云南自驾游 云南自驾游最优路线设计
1010
ij
w???
??r
i?1
j?1
?wij
(w
ij
?30tij
)
从而我们可以得到目标函数为:
Min w=w?+w??
=??rij
i?1
j?110
10
?wij
+
12
10
?
?
i?1
?4
?rij???wimrim?j?1?m?1
10
?
wr?jmjm?m?1?
4
①时间约束
时间包括在路途中需要的时间和在旅游景点逗留的时间。(www.61k.com] 因为t表示从第i个景区直达第j个景区路途中所需时间,所以路
ij
途中所需总时间为??rij
i?1
j?1
1010
?tij
;
im
jm
ti
表示旅游者在第i个景区的逗留时间, t,t表示旅游者在第
个景点的逗留时间,r,r表示出旅游
im
jm
i个景区和第j个景区的第m
者是否去第i个景区和第j个景区的第m个景点的0—1变量, 则 ti
4
?
?r
m?1
imim
t
,tj
4
?
?r
m?1
jm
tjm
故旅游者在旅游景区的总逗留时间为
12
10
10
?
??
i?1
j?1
?4
rij???rimtim?
?m?1
?
rt?jmjm? m?1?
4
因此,总的时间约束为:
10
10
??
i?1
j?1
rij?tij
+
12
1010
?
??
i?1
j?1
?4
rij???rimtim?
?m?1
?
rt?jmjm??m?1?
4
240
②旅游景区数约束
根据题目假设知,旅游者从昆明出发最终要回到昆明,整个旅游路线是环形,故旅游者旅游的景区数为??rij,这里我们假定要旅
i?1
j?110
10
5
云南自驾游 云南自驾游最优路线设计
游的景区数为n(n=2,3,??,10)。[www.61k.com] 因此旅游景区数约束为:
??rij=n (n=2,3,??,10)
i?1
j?110
10
③0——1变量约束
我们可以把所有的景区连成一个圈,而把每一个景区看做圈上一个点。对于每个点来说,只允许最多一条边进入,同样只允许最多一条边出来,并且只要有一条边进入就要有一条边出去。因此可得约束:
?r
i
ij
?
?r
j
ij
?1 (i,j=1,2,??,10)
?1;
?1。
i?1
当i?1时,因为昆明是出发点,所以?rij
当j?1时,因为代表们最终要回到昆明,所以?rij
j?1
综合以上可知,
?r
i
ij
?
?r
j
ij
?1 (i,j=1,2,??,10)
?r
i?1
ij
?1 ?rij?1
j?1
同样,当i,j?2时,假设不可能出现r
ij
?rji?1,即不可能出
现旅游者在两地间往返旅游,因为这样显然不满足游览景点尽量多的原则。因此我们可得约束:
rij?rji?0
(i,j=2,3,??,10)
综上所述,我们可以得到总的模型为:
Min w=w?+w??
=??rij
i?1
j?110
10
?wij
+
12
10
?
?
i?1
?4
?rij???wimrim?j?1?m?1
104
?w
m?1
jm
?
rjm?
?
6
云南自驾游 云南自驾游最优路线设计
约束条件:
1) ??rij
i?1
j?110
1010
10
?tij
+
12
1010
?
??
i?1
j?1
?4
rij???rimtim?
?m?1
?
rt?jmjm??m?1?
4
240
2) ??rij=n (n=2,3,??,10)
i?1
j?1
3) ?rij
i
?
?r
j
ij
?1 (i,j=1,2,??,10)
4) ?rij
i?1
?1 ?rij?1
j?1
5) r
ij
?rji?0
(i,j=2,3,??,10)
方案二:线路最短方案。(www.61k.com)放松时间约束,旅游者可以游遍所有的景区,该思路也就成了典型的推销员(TSP)问题。以游览的景点多,用时最少,消费最低为目标,建立模型,使用lingo软件求解得到最佳旅游路线。
要完成所有景区的旅游,而目标函数是求最少的交通费。由方案一的结论可知,旅游者所要出的总交通费用为:
10
10
ij
w???
??r
i?1
j?1
?wij
(w
ij
?30tij
)
因此,该问题的目标函数为:
Min w?????rij
i?1
j?110
10
?wij
(w
ij
?30tij
)
①时间约束
在这我们放松对时间的要求,我们不妨假定时间限制为一个月(720个小时),因此可得时间约束为:
10
10
ij
??r
i?1
j?1
?tij
+
12
1010
?
??
i?1
j?1
?4
rij???rimtim?
?m?1
4
?r
m?1
?tjmjm??
?
720
②旅游景区数约束
7
云南自驾游 云南自驾游最优路线设计
假定旅游者时间充裕,因此旅游者可以游览完全部10个景区。(www.61k.com]由方案一知道??rij表示旅游者游览的景区总数,因此该约
i?1j?11010
束为:
??rij
i?1j?11010?10 (i,j=1,2,??,10)
③旅游景点数约束
假定在旅游者游览10个景区的前提下必须游览的总景点数必须不小于于20,因为r表示出旅游者是否去第i个景区的第m个景im
点的0—1变量,故得到此约束为:
??rim
i?1m?1104?20;
总的旅游景区有10个,而一个景区有4个景点,所以旅游者游览的景点数不会超过40,即又得约束为:
104
im??r
i?1m?1?40.
④0——1变量约束
根据假设,整个旅游路线是环形,即最终旅游者要回到昆明,因此我们可以把整个路线看做一个Hamilton(哈密尔顿)圈,这样该问题就归结为货郎担(TSP)(哈密尔顿)问题,当然前提是我们已经知道了要旅游所有的景点。因此,对于Hamilton圈中的每个点来说,只允许有一条边进入,同样,也只允许有一条边出去。问题的重点在于找出最小权Hamilton圈,称这种圈为最优圈(H圈)。
设G=(V(G),E(G))是一无向连通图,其中 8
云南自驾游 云南自驾游最优路线设计
V(H)?(v1,v2,v3,v4,v5,v6,v7,v8,v9,v10),E(H)?(e1,e2,e3,e4,e5,e6,e7,e8,e9,e10),
我们将无向网络用三角不等式法转化为最优哈密尔顿回路(如图2所示)。(www.61k.com]
由附录4可知e8
圈G的一个改进。
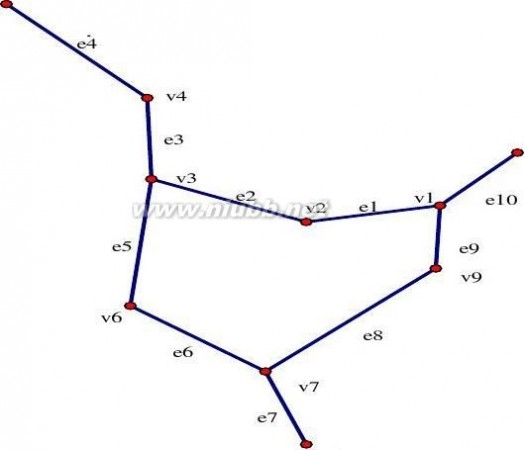
?e6?e5?e3?e4?2?e1?e10?e7?e9,则圈G
ij
将是
v8
v10
图1 各旅游景区分布及距离赋权图
c(k)?(vn,vi1,vi2,...,vi1,vin)
,则w(c
k
)?(wn,i1?wi1i2?...?wi1in)
为巡回总距
离,则,
目标: min
w(cH)?
?w(c)
k
CK?CH
cH
令决策变量为:
?{ck1,ck2,...,ckm}
9
云南自驾游 云南自驾游最优路线设计
xij
则
?1???0
若旅行者从vi到vj;
否则.
目标: min??wijxij
i?1
j?1
mn
约束条件: ?xkj
k?1
n
?1???m
j?1,...,n?1
j?n
n
i?1,...,n?1
i?n
?
k?1
?1xik??
?m
用公式表示即为:
?r
i
ij
?1 ?rij?1 (i,j
j
=1,2,??,10)
ij
同样,当i,j?2时,我们假设不可能出现r
?rji?1,即不可能出
现游客在两地间往返旅游,因为这样显然不满足游览景区尽量多的原则。(www.61k.com)因此我们可得约束:
rij?rji?0
(i,j=2,3,??,10)
综上所述,做对上述分析进步变换我们据第一方案思路可以得到总的模型为:
Min w?????rij
i?1
j?110
10
?wij
(w
ij
?30tij
)
约束条件:
1) ??rij
i?1
j?110
10
?tij
+
12
1010
?
??
i?1
j?1
?4
rij???rimtim?
?m?1
?
rt?jmjm??m?1?
4
720
2) ??rij
i?1
j?1
1010
?10
(i,j=1,2,??,10)
=1,2,??,10)
3) ?rij
i
?1 (i,j
10
云南自驾游 云南自驾游最优路线设计
4) ?rij
j
?1 (i,j=1,2,??,10)
5) r
ij
?rji?0
(i,j=2,3,??,10)
六、模型求解
通过上网查询资料,我们可以得到d的具体值,根据公式t=d/v
ij
ij
ij
可得到相应的t,同样根据公式w
ij
ij
ij
ij
?30tij
可以得到相应的w(i,j=1,
ij
2,??,10)。(www.61k.com](d、t和w的具体数值见附录4、5、6)
ij
方案一:通过对云南的一些旅行社上网进行咨询,我们得出旅游者在第i个景点的最佳逗留时间和他们在第i个景点总消费(如表1所示):
表1 旅游者在各景区的最佳逗留时间ti(单位:小时)

11
云南自驾游 云南自驾游最优路线设计
表2 旅游者在各景区的总消费(单位:元)

根据模型知,该模型为非线性规划模型,因此使用Lingo软件进行求解(程序见附录2)

,得出结果如表3: 表3 第一方案程序运行结果

12
云南自驾游 云南自驾游最优路线设计




注:vi(i=1,2,?,10)分别表示昆明、楚雄、大理、丽江、香格里拉、临沧、思茅、西双版纳、玉溪、曲靖.
13
云南自驾游 云南自驾游最优路线设计
基于上述结果,我们一般推荐线路为:
路线一:昆明→楚雄→大理→丽江→玉溪→昆明
旅游景点数:5 人均费用:155.8 元;
路线二:昆明→楚雄→大理→临沧→思茅→玉溪→曲靖→昆明
旅游景点数:7 人均费用:197.57 元;
路线三:昆明→楚雄→大理→临沧→思茅→西双版纳→玉溪→曲靖→昆明
旅游景点数:8 人均费用:205.5 元。[www.61k.com]
方案二:线路最短方案求解。
由于使用lingo求解,程序录入比较困难,因此此方案我们根据附录4的数据,使用MATLAB软件进行求解(程序见附录3),得出结果如下表:
表3 第二方案程序运行结果

七、模型评价及推广
优点:
1) 整篇文章思路比较简单,没有太多复杂的运算过程。
14
云南自驾游 云南自驾游最优路线设计
2) 方案一,未规定必须游览的景区数以及景点数,也就是旅游者可以对任何景区进行自由选择,可去可不去。(www.61k.com]
3) 方案二,在假定10个景区都必须游览,而且游览景点总数不少于20的条件下,建立模型,与现实中旅游者游览比较接近。
4) 利用的数据间的对比得到结果,比起复杂的计算过程更直观,更让人容易明白。
5) 求解出的最短路程,与实际路程基本保持一致。
6) 提供了优化方案,以供参考,模型短小精练,有很强的推广性,可由10个旅游景区推广至n个景区,旅游景点也可由4个推广至n个,都可以构造连通网络进行求解,此处不再进行求解。 缺点:
1)数据大部分参考互联网,数据缺乏一定的准确性。
2)没有考虑旅行路线以及行驶过程中会出现的实际情况,一切均
是最优考虑。
3)数据太多,列出来比较麻烦。
4)对于方案二用改良圈算法得到的结果几乎可以肯定不是最优
的。为了得到更高的精确度,可以选择不同的初始圈,重复进行几次算法,以求得较精确的结果。
5)方案二所采用的方法已被进一步发展,圈的修改过程一次替换三条边比一次仅替换两条边更为有效。
15
云南自驾游 云南自驾游最优路线设计
八、参考文献
[1] 姜启源?数学建模[J]?北京:高等教育出版社,2003年
[2] 白其峥?数学建模案例分析[J]?北京:海洋出版社,2000年
[3] 薛毅?动态规划,图论与网络模型?北京:北京工业大学出版社,2005年
[4] 陈东彦 李冬梅 王树忠,《数学建模》 科学出版社,2007年
[5] 党林立 孙晓群 《数学建模简明教程》 西安电子科技大学出版社,2009年
16
云南自驾游 云南自驾游最优路线设计
附录:
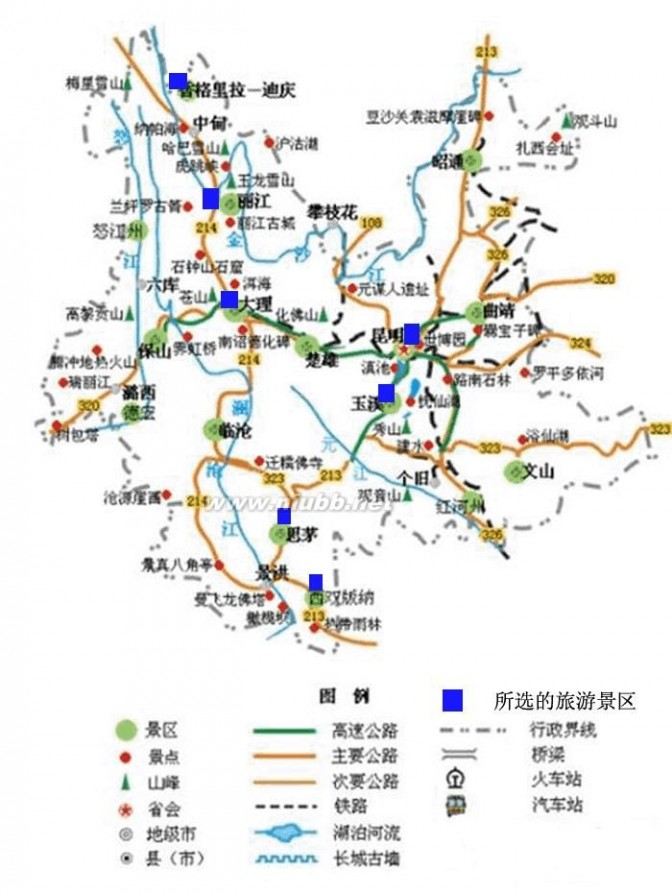
附录1 云南旅游景区分布图
17
云南自驾游 云南自驾游最优路线设计
附录2
方案一:消费最少路线,利用lingo 软件设计程序
程序如下:
Model:
sets:
jingdian/1..10/:c,t,l;
!其中:1,2,...,10分别代表昆明、楚雄、大理、丽江、香格里拉、临沧、思茅、西双版纳、玉溪、曲靖
;w,t分别表示旅行团在各景点的吃住消费和逗留时间;c表示各景点选择性权重;l是为了控制不出现两个以上环形回路而设的一个变量;
links(jingdian,jingdian):r,cc,tt;
!其中:r为0-1变量(0表示两景区不相连,1表示两景区相通);cc为两景区之间的交通费用;tt为两景区之间的交通时间; endsets
data:
t=8 10 20 34 10 32 13 25 35 23;
c=120 285 378 390 175 383 300 135 423 350;
tt=0 2.7 4.78 9.12 11.4 9.22 7.55 9.73 1.7 2.06
2.7 0 2.38 6.72 8.95 6.98 9.98 12.12 4 4.5
4.78 2.38 0 4.58 7 6.32 8.25 14.38 6.28 6.76
9.12 6.72 4.58 0 3.47 10.78 12.72 18.65 10.53 11.35
18
云南自驾游 云南自驾游最优路线设计
11.4 8.95 7 3.47 0 13.06 15 20.95 12.83 13.3
9.22 6.98 6.32 10.78 13.06 0 5.65 7.85 9.3 11.28
7.55 9.98 8.25 12.72 15 5.65 0 14.92 6.03 9.17
9.73 12.12 14.38 18.65 20.95 7.85 14.92 0 8.28 11.43
1.7 4 6.28 10.53 12.83 9.3 6.03 8.28 0 3.45
2.06 4.5 6.76 11.35 13.3 11.28 9.17 11.43 3.45 0;
!其中:主对角线为零,表示各景区到自身交通费用为零; cc=0 48 113 158 188 179 158 207 25 39 48 0 50 105 143 111 170 207 67 85 113 50 0 54 94 88 140 210 117 135
158 105 54 0 53 145 193 311 172 196 188 143 94 53 0 183 235 349 215 228 179 111 88 145 183 0 93 131 166 196 158 170 140 193 235 93 0 37 98 146
207 207 210 311 349 131 37 0 135 210 25 67 117 172 215 166 98 135 0 66 39 85 135 196 228 196 164 210 66 0; !其中:主对角线为零,表示各景区到自身的交通时间为零; n=?;
!其中:n表示计划游玩的景区数目;
enddata
19
云南自驾游 云南自驾游最优路线设计
min=@sum(jingdian(j):@sum(jingdian(i):r(i,j)*(cc(i,j)+0.5*(c(i)+c(j)))));
!目标函数:表示计划游玩的景区数目为n时的最小费用; @for(jingdian(i):r(i,i)=0);
!约束条件:表示各景点到自身没有路线相连的约束条件;
@for(jingdian(i)|i#ge#2:@for(jingdian(j)|j#ge#2:r(i,j)+r(j,i)<1));
!约束条件:表示除起点(昆明)外,若旅游者从景区i到景区j去游玩(即r(i,j)=1),则不会再从景区j到景区i去游玩(即r(j,i)=0),也就是说除起点外每个景区只游玩一次;
a=@sum(jingdian(j):@sum(jingdian(i):r(i,j)*(tt(i,j)+0.5*(t(i)+t(j)))));
@sum(jingdian(j):@sum(jingdian(i):r(i,j)*(tt(i,j)+0.5*(t(i)+t(j)))))<240;
!约束条件:表示总的旅行时间(交通时间和景区逗留时间)不超过给定时间10天240小时;
@for(jingdian(i):@sum(jingdian(j):r(i,j))=@sum(jingdian(j):r(j,i)));
@for(jingdian(i)|i#eq#1:@sum(jingdian(j):r(i,j))=1); @for(jingdian(i)|i#ne#1:@sum(jingdian(j):r(i,j))<1);
!这三个约束条件:表示起点(昆明)有且仅有一条路线出去和一条路线进来,其它景区要么有且仅有一条路线出去和一条路线进来,要 20
云南自驾游 云南自驾游最优路线设计
么既没有路线出去也没有路线进来;
@for(links:@bin(r));
!约束条件:表示0-1变量约束;
@sum(jingdian(j):@sum(jingdian(i):r(i,j)))=n;
!约束条件:表示旅游景区的数目为n的约束;
@for(jingdian(i):@for(jingdian(j)|j#gt#1#and#j#ne#i:l(j)>=l(i)+r(i,j)-(n-2)*(1-r(i,j))+(n-3)*r(j,i)));
@for(jingdian(i)|i#gt#1:l(i)<n-1-(n-2)*r(1,i);l(i)>1+(n-2)*r(i,1));
!这两个约束条件:为了控制不出现两个以上环形回路,保证有且仅有一条环形路线;
附录3
方案二:设计路线最短方案,利用MATLAB 软件求解
程序如下:
clc,clear
a(1,2)=160;a(1,3)=377;a(1,4)=527;a(1,5)=629.4;a(1,6)=598;a(1,7)=529;
a(1,8)=692;a(1,9)=86;a(1,10)=130;
a(2,3)=169.3;a(2,4)=352.2;a(2,5)=478.5;a(2,6)=372.7;a(2,7)=567.3;
a(2,8)=690;a(2,9)=225.5;a(2,10)=286.3;
21
云南自驾游 云南自驾游最优路线设计
a(3,4)=183.8;a(3,5)=314;a(3,6)=296.5;a(3,7)=469.3;a(3,8)=700;
a(3,9)=390.5;a(3,10)=451.2;
a(4,5)=178.5;a(4,6)=484.8;a(4,7)=657.7;a(4,8)=1039;a(4,9)=574.5;
a(4,10)=654.6;
a(5,6)=611;a(5,7)=783.8;a(5,8)=1164.8;a(5,9)=716.7;a(5,10)=761.3;
a(6,7)=312.4;a(6,8)=436.9;a(6,9)=554.1;a(6,10)=655; a(7,8)=124.7;a(7,9)=329.2;a(7,10)=547.8;
a(8,9)=451.4;a(8,10)=670;
a(9,10)=223.2;
a(10,:)=0;
a=a+a';
c1=[1 2:9 10];
L=length(c1);
flag=1;
while flag>0
flag=0;
for m=1:L-3
for n=m+2:L-1
if
22
云南自驾游 云南自驾游最优路线设计
a(c1(m),c1(n))+a(c1(m+1),c1(n+1))<a(c1(m),c1(m+1))+a(c1(n),c1(n+1))
flag=1;
c1(m+1:n)=c1(n:-1:m+1);
end
end
end
end
sum1=0;
for i=1:L-1
sum1=sum1+a(c1(i),c1(i+1));
end
circle=c1;
sum=sum1;
c1=[1 10 2:9];
flag=1;
while flag>0
flag=0;
for m=1:L-3
for n=m+2:L-1
if a(c1(m),c1(n))+a(c1(m+1),c1(n+1))<... a(c1(m),c1(m+1))+a(c1(n),c1(n+1))
23
云南自驾游 云南自驾游最优路线设计
flag=1;
c1(m+1:n)=c1(n:-1:m+1); end
end
end
end
sum1=0;
for i=1:L-1
sum1=sum1+a(c1(i),c1(i+1)); end
if sum1<sum
sum=sum1;
circle=c1;
end
circle,sum
24
云南自驾游 云南自驾游最优路线设计
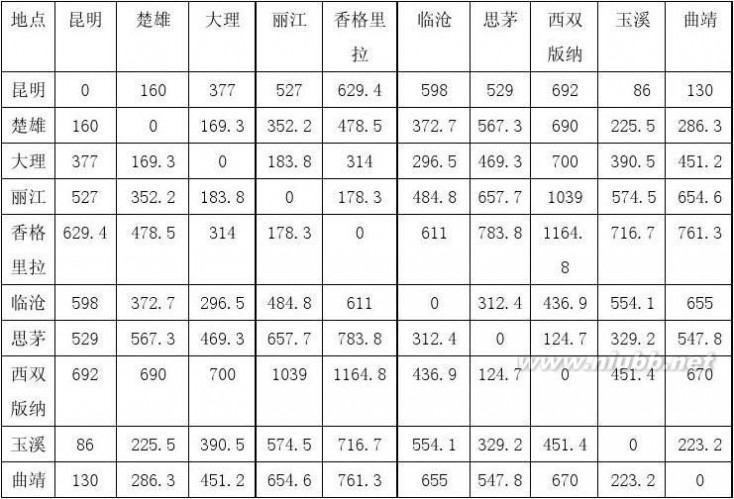
附录4 [d] 距离(单位:公里)
ij
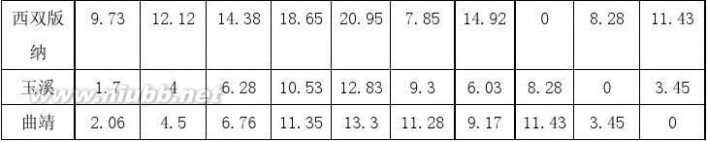
附录5 [tij]各景区间直达所需要的时间:(单位:小时)

25
云南自驾游 云南自驾游最优路线设计
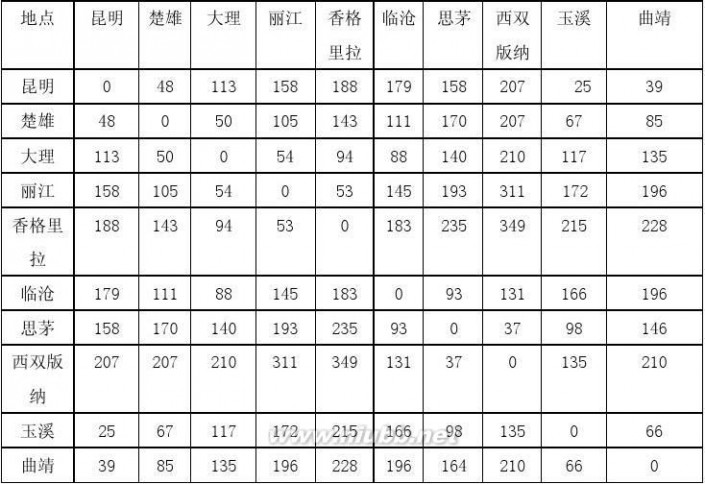
附录6 [wij]各景点间所需的交通费用:(单位:元)
26
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1