一 : 青海省海南州事业单位笔试成绩公告

青海省海南州事业单位笔试成绩公告

各位考生：

现将参加海南州2015年事业单位公开招聘工作人员笔试成绩进行公布，并对进入现场资格复审人员的笔试成绩进行公示，公示期为：2015年11月24日至11月30日；未进入现场资格复审人员的笔试成绩通过“个人笔试成绩查询”链接自行查询。(www.61k.com)现将资格复审的有关事项通知如下：

一、现场资格复审时间

2015年12月1日至12月4日，逾期视为自愿放弃。

二、现场资格复审地点

海南州人事考试中心（海南州人社局二楼东侧）

三、青海省海南州事业单位笔试成绩公告有关要求

1、凡进入现场资格复审的考生，请携带本人有效身份证（无身份证的可提供户籍部门出具的带照片的户籍证明）、户口簿、毕业证、笔试准考证、在中国高等教育学生信息网上打印的带有二维验证码的《教育部学历证书电子注册备案表》或《教育部学籍在线验证报告》及岗位要求的其他证件的原件和复印件。

2、按“少数民族”享受加分的考生要一并进行加分条件审核，凡不符合加分条件的，要取消加分并重新排列名次。

3、按各类服务项目条件报考的考生，须携带本人有效期内二代身份证、高校毕业生服务基层项目的相关证明、学历证书等证件的原件及复印件各一份。已经到现场进行服务基层项目加分审核并通过的考生，不用再提供服务项目相关证明。

4、获取国外学历、学位证书的考生须提供国家教育行政部门认证的学历认证报告。

5、按照《公告》要求，行政事业单位在职在编人员，现场资格复审时，须按要求提供用人单位、主管部门和同级人力资源社会保障部门同意报考的书面证明材料，否则，将取消招聘资格。

6、按照《公告》要求，招聘岗位数与报考人数达到1:3比例的按比例确定进入现场资格复审人员；达不到1:3比例的岗位笔试成绩须在40分以上方可进入现场资格复审。

7、各招聘岗位出现放弃（自动放弃资格复审的考生必须出具放弃承诺书，请考生将放弃承诺书及时发传真至0974-8512820）或现场资格审核不符合的考生，按照招聘公告空缺名额按笔试成绩从高到低依次递补。在现场资格复审期间原则上只递补一次。请各位考生随时关注招聘信息发布。

考生注意：逾期不来现场资格审查的、审查未通过的均不得进入下一环节。

附件：海南州2015年度事业单位公开招聘工作人员笔试成绩公示（点此链接）

首先，你要有一个概念，”编制很重要“。编制这个说法，是体制内的黑话。行政、事业、企业的编制，就其和体制内关系，依次递减。主要体现在，其经费来源和职能职权和待遇上。——青海省海南州事业单位笔试成绩公告

一、先解释下三者的意思：

1、公务员编制：先说公务员，公务员以前叫干部，后来改叫公务员了。是指依法履行公职、纳入国家行政编制，国家财政负担工资福利的工作人员。这句有三个重点：“依法履行公职”就不多说了，说白了公务员是国家法律的执行者，国家机器的组成者；所谓“公务员编制”的正规名字其实应该是指“行政编制”；国家财政负担，就是大家说的，“纳税人养着的”、“吃皇粮的”。

2、事业编制：事业编制就复杂了。这是中国特色的一类东西。用老话讲，事业单位本质是社会服务组织，介于行政机构和企事业单位之间；或者说，都有涉及。总之，涵盖特广，成分特杂。大概分以下几类：全额拨款、参照公务员、自收自支、财政补贴。具体分类区别就是其经费来源不同。另外，就事业单位的编制而言，很多部门都是既有行政编制，也有事业编制。

3、企业编制：既然涉及到编制，这个企业编制，不是说一般的企业员工。所谓企业编制，应该是在事业或者行政单位，但却是体制外的人员。就是俗话说的编外人员。这个说法应该是特指的。或者说是事业编制中自收自支的那一类。也被称作企业编制。

而现在的国有私营企业的员工，广义上也可以算是企业编制。但一般都不这么说。所以以下讨论的都是狭义的”企业编制“。不过也听说有的地方也有所谓的”企业编制“，说是裁员不会被先裁掉。

二、青海省海南州事业单位笔试成绩公告其区别为：

1、经费来源不一样：行政编制，国家财政全额负担；事业单位按不同的种类，由国家财政或全部或部分或一点不负担；企业编制理论上不管国家财政什么事。

2、待遇、地位不一样：这点在很多地方都有体现，一般来说，在体制内的行政或事业单位中，行政编制地位最高、待遇最好，这里所说的待遇包括工资、福利、升迁机会。而三者的稀缺程度也是依次递减，行政编制最少、最稀缺，事业编制多。这两种编制很占资源。所以国家严格限制其数量。但事情有需要那么多人做，so：企业编制，这玩意儿我怀疑是为了降低用工成本搞出来的。

3、职能职责不同：这个不用多说。理论上，公务员是”依法行政“的；而事业单位是全称是公益性事业单位，部分事业单位也有公共服务、行政的只能，部分其实是企业行政的，鉴于此事业编制也是这些职能；企业编制，我之前已经说了，算是体制外的。

三、优劣：

1、行政编制就是公务员，公务员的优势不必多说了。收入一般是个中产阶级。不算富，也不穷。还有希望奋斗成为官员。

2、事业编制待遇不一定比公务员差。因为公务员的监管日趋严格，而事业单位是和本身效益有关系的，也没有公务员那么严格的约束，很多事业单位钱是很多的。事业单位最终是会改革的，部分分流为行政编制，部分变成企业编制，剩下的才是正儿八经的公益性事业单位。

3、事业单位或者行政单位的企业编制的话，我个人意见是没什么前途，虽然待遇或许不差，但还会受一些歧视。所以，如果是这些单位的企业编制，就想办法走到体制内。

青海省海南州事业单位面试培训：

报名热线：0971—6240011；18997054800（石老师）13309787623（杨老师）

校区地址：西宁市城西区新宁广场对面王府井大楼2单元8楼

QQ客服：

微信客服：（扫一扫右侧二维码添加）

QQ/微信客服同号：941860332

善课思教育2015年青海省海南州事业单位面试培训：

报名热线：0971—6240011；18997054800（石老师）13309787623（杨老师）

校区地址：西宁市城西区新宁广场对面王府井大楼2单元8楼

QQ客服：

微信客服：（扫一扫右侧二维码添加）

QQ/微信客服同号：941860332

青海省海南州事业单位笔试成绩公告【我们承诺】：秉承一切为了学员，为了一切学员，为了学员一切的最有责任心、最人性化的办学理念，从您相信我们的那一刻开始，我们就已经决定不遗余力的为您的公考之路扫清任何障碍，助您轻松成“公”，请相信我们，我们将会用事实说话，用效果见证，用承诺为您公考保驾护航，0压力学习，0风险受训，让您培训无忧！只要是有利于您顺利通过公务员考试的：其他机构能做到的，我们就能做到；其他机构不能做到的，我们依然可以做到，其他机构承诺的，我们就能承诺；其他机构不能承诺的，我们依然可以给您承诺并很乐意承诺：

特别提醒#1您可以免费试听，我们给您这个权利，您不满意就退班，所以您无需怀疑我们；

特别提醒#2我们是免费培训；

特别提醒#3VIP班次训满万一不上，我们没有资格收您的钱，您不但可以分文不交，我们另外额外再赔您2800元；

（你们培训的风险，我们承担，您无需任何担忧，请您踏踏实实学习，轻轻松松过关！）

二 : 某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原

某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分均为100分．前6名选手的得分如下： 序号 项目 1 2 3 4 5 6 笔试成绩/分 85 92 84 90 84 80 面试成绩/分 90 88 86 90 80 85 根据规定，笔试成绩和面试成绩分别按一定的百分比折和成综合成绩（综合成绩的满分仍为100分） （1）这6名选手笔试成绩的中位数是______分，众数是______分． （2）现得知1号选手的综合成绩为88分，求笔试成绩和面试成绩个占的百分比． （3）求出其余五名选手的综合成绩，并以综合成绩排序确定前两名人选．

题型：解答题难度：中档来源：威海

（1）把这组数据从小到大排列为，80，84，84，85，90，92， 最中间两个数的平均数是（84+85）÷2=84.5（分）， 则这6名选手笔试成绩的中位数是84.5， 84出现了2次，出现的次数最多， 则这6名选手笔试成绩的众数是84； 故答案为：84.5，84； （2）设笔试成绩和面试成绩各占的百分百是x，y，根据题意得： x+y=1 85x+90y=88 ， 解得： x=0.4 y=0.6 ， 笔试成绩和面试成绩各占的百分比是40%，60%； （3）2号选手的综合成绩是92×0.4+88×0.6=89.6（分）， 3号选手的综合成绩是84×0.4+86×0.6=85.2（分）， 4号选手的综合成绩是90×0.4+90×0.6=90（分）， 5号选手的综合成绩是84×0.4+80×0.6=81.6（分）， 6号选手的综合成绩是80×0.4+85×0.6=83（分）， 则综合成绩排序前两名人选是4号和2号．

考点：

考点名称：平均数平均数：
是指在一组数据中所有数据之和再除以数据的个数。平均数是表示一组数据集中趋势的量数，它是反映数据集中趋势的一项指标。
解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数。
在统计工作中，平均数(均值)和标准差是描述数据资料集中趋势和离散程度的两个最重要的测度值。平均数的分类:
（1）算术平均数：一般地，如果有n个数 ，那么 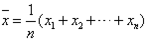，叫做这n个数的算术平均数。
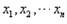（2）加权平均数：一组数据点的权分别为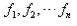，那么称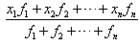为这n个数的加权平均数。
（3）样本平均数：样本中所有个体的平均数。
（4）总体平均数：总体中所有个体的平均数，统计学中常用样本的平均数估计总体的平均数。

平均数、中位数和众数关系:
联系:
平均数、中位数和众数都是来刻画数据平均水平的统计量，它们各有特点。对于平均数大家比较熟悉，中位数刻画了一组数据的中等水平，众数刻画了一组数据中出现次数最多的情况。
平均数非常明显的优点之一是，它能够利用所有数据的特征，而且比较好算。另外，在数学上，平均数是使误差平方和达到最小的统计量，也就是说利用平均数代表数据，可以使二次损失最小。因此，平均数在数学中是一个常用的统计量。但是平均数也有不足之处，正是因为它利用了所有数据的信息，平均数容易受极端数据的影响。
例如，在一个单位里，如果经理和副经理工资特别高，就会使得这个单位所有成员工资的平均水平也表现得很高，但事实上，除去经理和副经理之外，剩余所有人的平均工资并不是很高。这时，中位数和众数可能是刻画这个单位所有人员工资平均水平更合理的统计量。
中位数和众数这两个统计量的特点都是能够避免极端数据，但缺点是没有完全利用数据所反映出来的信息。
由于各个统计量有各自的特征，所以需要我们根据实际问题来选择合适的统计量。
当然，出现极端数据不一定用中位数，一般，统计上有一个方法，就要认为这个数据不是来源于这个总体的，因而把这个数据去掉。比如大家熟悉的跳水比赛评分，为什么要去掉一个最高分、一个最低分呢，就认为这两个分不是来源于这个总体，不能代表裁判的鉴赏力。于是去掉以后再求剩下数据的平均数。需要指出的是，我们处理的数据，大部分是对称的数据，数据符合或者近似符合正态分布。这时候，均值(平均数)、中位数和众数是一样的。

区别:
只有在数据分布偏态(不对称)的情况下，才会出现均值、中位数和众数的区别。所以说，如果是正态的话，用哪个统计量都行。如果偏态的情况特别严重的话，可以用中位数。
除了需要刻画平均水平的统计量，统计中还有刻画数据波动情况的统计量。比如，平均数同样是5，它所代表的数据可能是1、3、5、7、9，可能是4、4.5、5、5.5、6。也就是说5所代表的不同组数据的波动情况是不一样的。怎样刻画数据的波动情况呢?很自然的想法就是用最大值减最小值，即求一组数据的极差。数学中还有方差、标准差等许多用来刻画数据特征的统计量。当然这些都是教师感兴趣、值得了解的内容，不是小学数学的教学要求。

平均数的求法：
（1）公式法： ；
（2）加权平均数公式：。
考点名称：中位数和众数中位数：一般地，n个数据按大小顺序排列，处于最中间位置的一个数据（或最中间位置的两个数据的平均数）叫这组数据的中位数。
众数：在一组数据中，出现次数最多的数据。 中位数的位置：
当样本数为奇数时，中位数=(N+1)/2;当样本数为偶数时，中位数为N/2与1+N/2的均值

众数性质：
用众数代表一组数据，可靠性较差，不过，众数不受极端数据的影响，并且求法简便。在一组数据中，如果个别数据有很大的变动，选择中位数表示这组数据的“集中趋势”就比较适合。
当数值或被观察者没有明显次序（常发生于非数值性资料）时特别有用，由于可能无法良好定义算术平均数和中位数。例子：{鸡、鸭、鱼、鱼、鸡、鱼}的众数是鱼。
众数算出来是销售最常用的，代表最多的
众数是在一组数据中,出现次数最多的数据
两组数据中,都是1,2出现次数最多
所以1,2是众数
众数：
一般来说，一组数据中，出现次数最多的数就叫这组数据的众数。
例如：1，2，3，3，4的众数是3。
但是，如果有两个或两个以上个数出现次数都是最多的，那么这几个数都是这组数据的众数。
例如：1，2，2，3，3，4的众数是2和3。
还有，如果所有数据出现的次数都一样，那么这组数据没有众数。
例如：1，2，3，4，5没有众数。
在高斯分布中，众数位于峰值。

平均数、中位数和众数的特征：
（1）平均数、中位数、众数都是表示一组数据“平均水平”的平均数。
（2）平均数能充分利用数据提供的信息，在生活中较为常用，但它容易受极端数字的影响，且计算较繁。
（3）中位数的优点是计算简单，受极端数字影响较小，但不能充分利用所有数字的信息。 中位数算出来可避免极端数据，代表着数据总体的中等情况。
（4）众数的可靠性较差，它不受极端数据的影响，求法简便，当一组数据中个别数据变动较大时，适宜选择众数来表示这组数据的“集中趋势”。

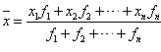平均数、中位数和众数异同：
一、相同点
平均数、中位数和众数这三个统计量的相同之处主要表现在：都是来描述数据集中趋势的统计量；都可用来反映数据的一般水平；都可用来作为一组数据的代表。

二、不同点
它们之间的区别，主要表现在以下方面。
1、定义不同
平均数：一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数。
中位数：将一组数据按大小顺序排列，处在最中间位置的一个数叫做这组数据的中位数 。
众数：在一组数据中出现次数最多的数叫做这组数据的众数。

2、求法不同
平均数：用所有数据相加的总和除以数据的个数,需要计算才得求出。
中位数：将数据按照从小到大或从大到小的顺序排列，如果数据个数是奇数，则处于最中间位置的数就是这组数据的中位数；如果数据的个数是偶数，则中间两个数据的平均数是这组数据的中位数。它的求出不需或只需简单的计算。
众数：一组数据中出现次数最多的那个数，不必计算就可求出。

3、个数不同
在一组数据中，平均数和中位数都具有惟一性，但众数有时不具有惟一性。在一组数据中，可能不止一个众数，也可能没有众数。

4、呈现不同
平均数：是一个“虚拟”的数，是通过计算得到的，它不是数据中的原始数据。
中位数：是一个不完全“虚拟”的数。当一组数据有奇数个时，它就是该组数据排序后最中间的那个数据，是这组数据中真实存在的一个数据；但在数据个数为偶数的情况下，中位数是最中间两个数据的平均数，它不一定与这组数据中的某个数据相等，此时的中位数就是一个虚拟的数。
众 数：是一组数据中的原数据 ，它是真实存在的。

5、代表不同
平均数：反映了一组数据的平均大小，常用来一代表数据的总体 “平均水平”。
中位数：像一条分界线，将数据分成前半部分和后半部分，因此用来代表一组数据的“中等水平”。
众数：反映了出现次数最多的数据，用来代表一组数据的“多数水平”。
这三个统计量虽反映有所不同，但都可表示数据的集中趋势，都可作为数据一般水平的代表。

6、特点不同
平均数：与每一个数据都有关,其中任何数据的变动都会相应引起平均数的变动。主要缺点是易受极端值的影响，这里的极端值是指偏大或偏小数，当出现偏大数时，平均数将会被抬高，当出现偏小数时，平均数会降低。
中位数：与数据的排列位置有关，某些数据的变动对它没有影响；它是一组数据中间位置上的代表值，不受数据极端值的影响。
众数：与数据出现的次数有关，着眼于对各数据出现的频率的考察，其大小只与这组数据中的部分数据有关，不受极端值的影响,其缺点是具有不惟一性，一组数据中可能会有一个众数，也可能会有多个或没有 。

7、作用不同
平均数：是统计中最常用的数据代表值，比较可靠和稳定，因为它与每一个数据都有关，反映出来的信息最充分。平均数既可以描述一组数据本身的整体平均情况，也可以用来作为不同组数据比较的一个标准。因此，它在生活中应用最广泛，比如我们经常所说的平均成绩、平均身高、平均体重等。
中位数：作为一组数据的代表，可靠性比较差，因为它只利用了部分数据。但当一组数据的个别数据偏大或偏小时，用中位数来描述该组数据的集中趋势就比较合适。
众数：作为一组数据的代表，可靠性也比较差，因为它也只利用了部分数据。。在一组数据中，如果个别数据有很大的变动，且某个数据出现的次数最多，此时用该数据（即众数）表示这组数据的“集中趋势”就比较适合。

中位数、众数的求法：
中位数：
①将数据按大小顺序排列；
②当数据个数为奇数时，中间的那个数据就是中位数；
当数据个数为偶数时，居于中间的两个数据的平均数才是中位数。

众数：找出频数最多的数据，若几个数据频数最多且相同，此时众数就是这几个数据。

三 : 小事成绩单

    今天是2012年4月26日，星期四。晚上回到家，我打开电脑，上上了现代最潮流的QQ，便看到了184班的群，里面有一个 共享文件 184班成绩表。我欣喜若狂的下载了成绩单，又喜又悲的打开了表，一场忧伤的事诞生了：我只考了全班第8，前三门考的都不错！我很高兴！但一看到后面的"综合成绩"，我好不可思议呀，竟、竟然才考了那么一点点

    山西晋中太行小学五年级:田芷行

本文标题：事业单位笔试成绩-青海省海南州事业单位笔试成绩公告
本文地址： http://www.61k.com/1067082.html