一 : 性生活中的各种美学问题!:身体与性器官的美学
夫妻性生活,不仅可以缔造卿卿我我的、至爱亲情和甜美的婚姻,还蕴涵着极高的美学意义。波兰著名性学家K·伊莫林斯基曾指出:"注意性生活的美学有极其重要的意义,若忽视了这方面的价值,便会对性生活发生强烈的抑制作用,导致某些性失调和心理失衡。"
那么,在性生活中需要注意哪些美学问题呢?
身体与性器官的美学
在性生活中,身体和性器官的清洁卫生不仅具有卫生学意义,也具有十分重要的美学意义。夫妻任何一方不清洁的接触,均可引起不愉快的反应,并成为妨碍双方性交的强烈抑制因素。不洁或异味,都有可能在女方的心灵上造成一种厌弃心理,削弱美感中的激奋情绪。
衣着和风度的美学
衣着美和风度美,对夫妻性生活的和谐有相当影响。所以,女人一般都很注重在服饰、体态、眼神、言行、举止上下功夫。但有的女性,成其是进入中年的女人,却常忽视这一点。
为人之妻,应该明白,男人不希望妻子过早成为老气横秋的"黄脸婆"。相对而言,男性的视觉更灵敏。所以,衣着和风度上的女性美,实际上是开启男人性爱的闸门。反之,丈夫衣着的清洁与否,对妻子来说同样如此。
性交准备中的美学
性交准备工作是多方面的,心理审美上的准备也是其一。
我们知道,心理上的性冲动,往往是在夫妻之间亲密、温馨的氛围中产生的。只有在绵绵情意中,才能使爱情得以升华、净化。
如果忽视了性心理准备中的美学问题,就很难激发出惬意的做爱心绪。男女都是用爱来塑造世界的,情爱是性爱的基础。没有情爱,性爱便是空中楼阁。相反,没有和谐的性爱,爱情便是纸上谈兵。此外,性交准备中的美学,还表现在审美观上,如夫妻双方房事的穿衣问题。
如果妻子很懂得穿内衣的艺术,对激发丈夫的感情有极大作用,而且女性的半遮半露,比赤裸裸的暴露对男人的刺激作用更大。因为全裸的肌肤容易破坏心理欲望的神秘感,不容易让男人一下产生出美感来。相比之下,那种似遮似露的衣着,却能充分展示女性特有的神韵,给人以朦胧美。
性爱环境中的美学
性爱环境中的美学,也是性生活美学的一个重要因素。充满"爱的氛围"的性爱环境,对性生活质量有着重要意义。 那么,如何才能创造一个爱意浓浓的性爱氛围呢?
卧室的色彩、摆设、光线是构成性和谐最佳环境的必要条件。在卧室的色调要以妻子的需求为宜。一般来说,热情、开朗的妻子,应使用细腻、表现力丰富的软色彩;拘谨、内向的妻子,宜选择明朗、欢快的色彩。
床上用品与家具的摆设,总体上要取暖色,以增强温馨、甜蜜的气氛。卧室里的灯具尽量选用亮度可调的壁灯、台灯或吊灯。做爱之前,可将其调成暗而柔和的光线,创造一种朦胧的意境。性学家的研究表明,夫妻在柔和的光线中观察对方性唤起时的状态,及个人的性生理反应,可以强化双方的性兴奋。
总之,注意夫妻性生活中美学问题,不仅可使夫妻性生活进入一种美的境界,而且能促进夫妻间的性修养。
二 : 赌马中的数学问题
赌马中的数学问题
随着中国的改革开放,境外许多事物渐渐被生活在大陆的人知晓诸如赌马、六合彩等常在媒体中提及。(www.61k.com]对我们来说,了解一些原来不熟悉的东西也是必要的。其实,一些博彩游戏和古老的赌博有许多相似之处,我们可以用初等概率知识对其中的现象作一定的分析。
我们以赌马问题为例。为简便起见,假设只有两匹马参加比赛。通过对决定马匹胜负的各因素的研究以及对以往赛事胜负情况的统计分析,我们可得出两匹马各自胜出的实际概率。不失一般性,设其中一匹马胜出的实际概率为一匹马胜出的实际概率为
们能赢得钱呢?
要解决这个问题必须先弄明白庄家的赔率是如何设定的。所谓赔率,是指押注一元钱于胜方所获得的总金额。举例来说,若赔率为1.65元,则如押注一元的一方恰好胜出,可得收益0.65元,加上本金,一共可得1.65元。若押注负方,则会失去所押注的1元,但不须另外再输钱。现在,我们知道了马匹胜出的实际概率,知道了庄家设定的赔率,就可以分析参赌者该如何下注。这里,设总金额为1元,并设在第一匹马上押注元,则在第二匹马上押注。至于具体押注,则另。那么,参赌者该如何下注以最大的限度确保他多少,参赌者可以将总金额按该比例分配给这两匹马。于是,可得下表:
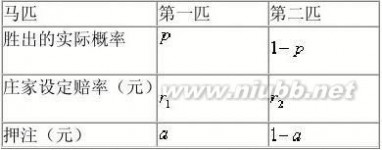
如果第一匹马赢,参赌者可得到
为元,再减去付出的1元,参赌者的收益元。考虑到两元;同理,如果第二匹马赢,参赌者收益为
赌马 赌马中的数学问题
匹马胜出的实际概率分别为和

,其中,参赌者的期望收益为。[www.61k.com)另外,若参赌者把所有钱都押注于第一匹马时期望收益为
望收益为。 ;若参赌者把所有的钱都押注于第二匹马时,期自然,参赌者希望收益
要求:,这样,他们才能以一个正的概率赢利。所以。
1)当,且,即当

且时,不论取何值,
。实际上,当

恒大于0,且当趋向1时,

趋向于极大值,即参赌者把钱全押注于第一匹马上时,有收益
,所以参赌者应当把钱全部押注于第一匹马上。
2)当时,收益实际上,当

且,即当趋于极大值且。随着的变大而变小,且当趋于0时,,即参赌者把钱全押注于第二匹马上时,有收益
。所以参赌者应当把钱全押在第二匹马上。
3)当,时,为使,应满足:

。又∵,∴,即。即当

,且时,参赌者按分配赌注可期望赢利。且当趋向于1
赌马 赌马中的数学问题
时,收益趋于极大值。[www.61k.com]同1)情况可知,这时,参赌者应把钱全押注于。 第一匹马上,有收益
4)当,且时。
这时不论赌注如何分配,参赌者的期望收益恒为负。在这情况下,参赌者介入其中是不理智的行为。
以上是参赌者在已知胜出概率及赔率时选择的策略。同样,庄家在设置赔率时,一定会对实际各匹马胜出的概率作一番认真研究,由此设定相应赔率。这样,他才有可能不赔本。由此当庄家设置一个赔率时,我们也可以反推庄家所估计的各匹马胜出的概率。例如,庄家赔率设定为15,则我们大致可以知道该马匹胜出概率大致应小于。
其实,在其它涉及赔率、押注的简单模型中,我们也可以用相应的方法进行分析。当然,这只是对实际情况的一种简化。现实生活中的赌马不会仅有两匹,并且要求出各马匹实际胜出的概率是件非常困难的事,在一般情况下,只能求得近似解。
三 : 初中数学实际生活中的应用问题
一、商品定价问题:
例1 某种品牌的彩电降价30%以后,每台售价为元,则该品牌的彩电每台原价为
二、商品降价问题:
例2 某商品进价是1000元,售价是1500元。由于销售情况不好,商店决定降价出售,但又要保证利润为5% ,求商店应降价多少元出售。
三、存款利率问题:
例3 国家规定存款利息的纳税办法是:利息税=利息×20% ,储户取款时由银行代扣代收。若银行一年定期储蓄的年利率为2.25% ,某储户取出一年到期的本金及利息时,扣除了利息税36元,则银行向该储户支付的现金是多少元?
四、支付稿酬问题
例4 国家规定个人发表文章或出书获得稿费的纳税计算方法是:(1)稿费不高于800元的,不纳税;(2)稿费高于800元又不高于4000元的应交超过800元那一部分稿费的14% 的税;(3)稿费高于4000元的应交全部稿费的11% 的税。王老师曾获得一笔稿费,并交税280元,算一算王老师这笔稿费是
五、股票问题:
例5 下表是某一周甲、乙两种股票每天的收盘价(每天交易结束时的价格)
收 盘 名 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 四 : 生活中的数学问题 很多人都认为数学是一门 很枯燥的学科, 很枯燥的学科,的确数学理论 性很强需要很多抽象思考, 性很强需要很多抽象思考, 但是在数学发展的中也发生了 很多有意思的事情, 很多有意思的事情,它可以让 你充分体会到数学的乐趣! 你充分体会到数学的乐趣! 并在其中掌握数学知识。 并在其中掌握数学知识。 小格内给两粒,第三格内给四粒, 样下去,每一小格内都比前一小格加一倍。陛下,把这样摆满 样下去,每一小格内都比前一小格加一倍。陛下, 棋盘上所有64格的麦粒,都赏给您的仆人吧! 64格的麦粒 棋盘上所有64格的麦粒,都赏给您的仆人吧!’ ‘爱卿,你所求的并不多啊。”国王说道,心里为自己对这 样一件奇妙的发明赏赐的许诺不致破费太多而暗喜。“你当然会 如愿以偿的,”国王命令如数付给达依尔。 计数麦粒的工作开始了,第一格内放1粒,第二格内放2粒 第三格内放2’粒,…还没有到第二十格,一袋麦子已经空了。 一袋又一袋的麦子被扛到国王面前来。但是,麦粒数一格接一格 飞快增长着,国王很快就看出,即便拿全印度的粮食,也兑现不 了他对达依尔的诺言。 ? 11分钟时候是半篮子鸡蛋 分钟时候是半篮子鸡蛋 案 本文地址: http://www.61k.com/1066953.html 61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1 |