一 : 10几种湍流模型

解决湍流的模型总计就是那几个方程，Fluent又从工程和数值的角度进行了整理，下面就是这些湍流模型的详细说明。 FLUENT 提供了以下湍流模型： ·Spalart-Allmaras 模型 ·k-e 模型 －标准k-e 模型 －Renormalization-group (RNG) k-e模型 －带旋流修正k-e模型 ·k-ω模型 －标准k-ω模型 －压力修正k-ω模型 雷诺兹压力模型 大漩涡模拟模型

几个湍流模型的比较：

从计算的角度看Spalart-Allmaras模型在FLUENT中是最经济的湍流模型，虽然只有一种方程可以解。由于要解额外的方程，标准k-e模型比Spalart-Allmaras模型耗费更多的计算机资源。带旋流修正的k-e模型比标准k-e模型稍微多一点。由于控制方程中额外的功能和非线性，RNGk-e模型比标准k-e模型多消耗10～15%的CPU时间。就像k-e模型，k-ω模型也是两个方程的模型，所以计算时间相同。

比较一下k-e模型和k-ω模型，RSM模型因为考虑了雷诺压力而需要更多的CPU时间。然而高效的程序大大的节约了CPU时间。RSM模型比k-e模型和k-ω模型要多耗费50～60%的CPU时间，还有15～20%的内存。

除了时间，湍流模型的选择也影响FLUENT的计算。比如标准k-e模型是专为轻微的扩散设计的，然而RNG k-e模型是为高张力引起的湍流粘度降低而设计的。这就是RNG模型的缺点。 同样的，RSM模型需要比k-e模型和k-ω模型更多的时间因为它要联合雷诺压力和层流。

概念：

1.雷诺平均：在雷诺平均中，在瞬态N-S方程中要求的变量已经分解为时均常量和变量。 相似的，像压力和其它的标量

?i?i??i'???(10.2?2)

这里?表示一个标量如压力，动能，或粒子浓度。

2. Boussinesq逼近从雷诺压力转化模型：利用Boussinesq假设把雷诺压力和平均速度梯度联系起来：

Boussinesq假设使用在Spalart-Allmaras模型、k-e模型和k-ω模型中。这种逼近方法好处是对计算机的要求不高。在Spalart-Allmaras模型中只有一个额外的方程要解。k-e模型和k-ω模型中又两个方程要解。Boussinesq假设的不足之处是假设ut是个等方性标量，这是不严格的。

1．Spalart-Allmaras 模型（1equ）：

方程是：

这里Gv是湍流粘度生成的，Yv是被湍流粘度消去，发生在近壁区域。S~是用户定义的。注意到湍流动能在Spalart-Allmaras没有被计算，但估计雷诺压力时没有被考虑。 特点：

1）. Spalart-Allmaras 模型是设计用于航空领域的，主要是墙壁束缚流动，而且已经显示出和好的效果。

2）。在原始形式中Spalart-Allmaras 模型对于低雷诺数模型是十分有效的，要求边界层中粘性影响的区域被适当的解决。

3）。不能依靠它去预测均匀衰退，各向同性湍流。还有要注意的是,单方程的模型经常因为对长度的不敏感而受到批评，例如当流动墙壁束缚变为自由剪切流。

2．k-e模型（2equ）：

2.1、标准k-e模型的方程

湍流动能方程k，和扩散方程e：

方程中Gk表示由层流速度梯度而产生的湍流动能，计算方法在10.4.4中有介绍。Gb是由

浮力产生的湍流动能，10.4.5中有介绍，YM由于在可压缩湍流中，过渡的扩散产生的波动，10.4.6中有介绍，C1，C2，C3，是常量，σk和σe是k方程和e方程的湍流Prandtl数，

Sk和Se是用户定义的。

特点：

标准k-e模型自从被Launder and Spalding提出之后，就变成工程流场计算中主要的工具了。适用范围广、经济、合理的精度，这就是为什么它在工业流场和热交换模拟中有如此广泛的应用了。它是个半经验的公式，是从实验现象中总结出来的。

2.2、RNG k-e模型（2equ）：

RNG k-e 模型的方程

Gk是由层流速度梯度而产生的湍流动能，10.4.4介绍了计算方法，Gb是由浮力而产

生的湍流动能，10.4.5介绍了计算方法，YM由于在可压缩湍流中，过渡的扩散产生的波动，10.4.6中有介绍，C1，C2，C3，是常量，ak和ae是k方程和e方程的湍流Prandtl数，Sk和Se是用户定义的。

RNG和标准k-e模型的区别在于：

这里

特点：

RNG k-e模型来源于严格的统计技术。它和标准k-e模型很相似，但是有以下改进： ·RNG模型在e方程中加了一个条件，有效的改善了精度。 ·考虑到了湍流漩涡，提高了在这方面的精度。 ·RNG理论为湍流Prandtl数提供了一个解析公式，然而标准k-e模型使用的是用户提供的常数。

·然而标准k-e模型是一种高雷诺数的模型，RNG理论提供了一个考虑低雷诺数流动粘性的解析公式。这些公式的效用依靠正确的对待近壁区域

这些特点使得RNG k-e模型比标准k-e模型在更广泛的流动中有更高的可信度和精度。

1. 带旋流修正的 k-e模型（2equ）：

带旋流修正k-e模型的方程

在方程中，Gk是由层流速度梯度而产生的湍流动能，10.4.4介绍了计算方法，Gb是由浮力而产生的湍流动能，10.4.5介绍了计算方法，YM由于在可压缩湍流中，过渡的扩散产生的波动，10.4.6中有介绍， C2，C1e是常量，σk和σe是k方程和e方程的湍流Prandtl数，Sk和Se是用户定义的。 特点：

带旋流修正的 k-e模型和RNG k-e模型都显现出比标准k-e模型在强流线弯曲、漩涡和旋转有更好的表现。由于带旋流修正的 k-e模型是新出现的模型，所以现在还没有确凿的证据表明它比RNG k-e模型有更好的表现。但是最初的研究表明带旋流修正的 k-e模型在所有k-e模型中流动分离和复杂二次流有很好的作用。

带旋流修正的 k-e模型的一个不足是在主要计算旋转和静态流动区域时不能提供自然的湍流粘度。这是因为带旋流修正的 k-e模型在定义湍流粘度时考虑了平均旋度的影响。这种额外的旋转影响已经在单一旋转参考系中得到证实，而且表现要好于标准k-e模型。由于这些修改，把它应用于多重参考系统中需要注意。

3．k-ω模型（2equ）：

3.1、标准k-ω模型的方程

在方程中，Gk是由层流速度梯度而产生的湍流动能。Gω是由ω方程产生的。Tk和Tω

表明了k和ω的扩散率。Yk和Yω由于扩散产生的湍流。，所有的上面提及的项下面都有介绍。Sk和Se是用户定义的。

特点：

标准k-ω模型是基于Wilcox k-ω模型，它是为考虑低雷诺数、可压缩性和剪切流传播而修改的。Wilcox k-ω模型预测了自由剪切流传播速率，像尾流、混合流动、平板绕流、圆柱绕流和放射状喷射，因而可以应用于墙壁束缚流动和自由剪切流动。

3.2、剪切压力传输（SST） k-ω模型（2equ）：

SST K-?流动方程：

其方程：

和

方程中， Gk表示湍流的动能，扩散项

，

分别代表k与?的发散项。

代表正交发散项。

与

用户自定义。

为?方程，

，

分别代表k与?的有效

这个公式与标准K-?模型不同，区别在于标准K-?中，方程如下：

为一常数，而SST模型中，

10几种湍流模型_湍流模型

其中：

特点：

SST k-ω模型和标准k-ω模型相似，但有以下改进：

·SST k-ω模型和k-e模型的变形增长于混合功能和双模型加在一起。混合功能是为近壁区域设计的，这个区域对标准k-ω模型有效，还有自由表面，这对k-e模型的变形有效。

·SST k-ω模型合并了来源于ω方程中的交叉扩散。

·湍流粘度考虑到了湍流剪应力的传波。

·模型常量不同

这些改进使得SST k-ω模型比标准k-ω模型在在广泛的流动领域中有更高的精度和

可信度。

四．雷诺压力模型（RSM）：

雷诺应力流动方程：

在这些项中，不需要模型，

而需要建立模型方程使方程组封闭

特点：

由于RSM比单方程和双方程模型更加严格的考虑了流线型弯曲、漩涡、旋转和张力快速变化，它对于复杂流动有更高的精度预测的潜力。但是这种预测仅仅限于与雷诺压力有关的方程。压力张力和耗散速率被认为是使RSM模型预测精度降低的主要因素。 RSM模型并不总是因为比简单模型好而花费更多的计算机资源。但是要考虑雷诺压力的各向异性时，必须用RSM模型。例如飓风流动、燃烧室高速旋转流、管道中二次流。

五．大涡模拟：

传统的流场计算方法是用N-S方程，即RANS法，在此方法制，所有的湍流流场都可以模拟，其结果可保存。理论上，LES法处于DNS与RANS之间，大尺寸漩涡用LES法，而小尺寸的漩涡用RANS方程求解，使用LES法的原则如下：

（1）动量，质量，能量主要由大尺寸漩涡传输；

（2）大涡在流动中期主导作用，它们主要由流动的几何，边界条件来确定。

（3）小涡不起主导作用（尺寸上），单其解决方法更具有通用性

（4）当仅有小涡时，更容易建立通用的模型

当解决仅有大涡否则仅有小涡的问题时，所受的限制要比DNS法少的多。然而在实际工程中，需要很好的网格划分，这需要很大的计算代价，只有计算机硬件性能大幅提高，或者采用并行运算，LES才可能用于实际工程。

二 : 湍流模型是什么

湍流模型 -简介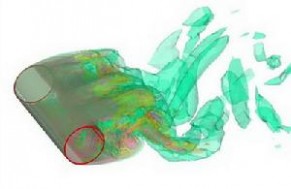湍流模型，就是以雷诺平均运动方程与脉动运动方程为基础，依靠理论与经验的结合，引进一系列模型假设，而建立起的一组描写湍流平均量的封闭方程组。 本文标题：湍流模型-10几种湍流模型
本文地址： http://www.61k.com/1065442.html