一 : 计算机算法分析与设计论文
计算机学院
算法设计与分析课程考查论文
题 目0-1背包问题的算法设计策略对比与分析 专 业
班 级
学 号
姓 名 任课教师 0-1背包问题的算法设计策略对比与分析 引言
算法,是在有限步骤内求解某一问题所使用的一组定义明确的规则。(www.61k.com)通俗点说,就是计算机解题的过程。在这个过程中,无论是形成解题思路还是编写程序,都是在实施某种算法。前者是推理实现的算法,后者是操作实现的算法。
算法分析与设计 计算机算法分析与设计论文
对于程序员来说,算法的概念是至关重要的。(www.61k.com)因为它是程序的灵魂,是一系列解决问题的清晰指令,也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。懂得了算法,就相当于领悟到了程序的灵魂,这样写起程序也会感到是一种惬意。但不同的算法可能用不同的时间、空间或效率来完成同样的任务。所以算法也有优劣,也有高效与低效之分。
一个算法应该具有以下五个重要的特征:有穷性、确切性、输入、输出、可行性。但我认为这些都是算法应该具备的最基本的特征,如果没了这些,我们又为什么花费心思学习它呢,所以这些并不是让我们热衷算法的资本。高效,才是所有程序员所向往的,而算法又恰恰能满足人们对高效的要求,也正因为此,我才会在这写有关贪心算法的心得。
所谓贪心算法指的是为了解决在不回溯的前提之下,找出整体最优秀或者接近最优解的这样一种类型的问题而设计出来的算法。贪心算法的基本思想是找出整体当中每个小小局部的最优解,并且将所有的这些局部最优解合起来形成整体上的一个最优解。
有人说贪心算法在解决问题的策略上目光短浅,只根据当前已有的信息就做出选择,而且一旦做出了选择,不管将来有什么结果,这个选择都不会改变。换言之,也就是说贪心法并不是从整体最优考虑,它所做出的选择只是在某种意义上的局部最优。
但我认为这种局部最优选择虽然并不总能获得整体最优解(Optimal Solution),但通常能获得近似最优解(Near-Optimal Solution),所以还是一种高效的选择。接下来就让我们用实例来感受贪心算法的高效和思想。
贪心算法的基本思路和实现过程
基本思路:
1 建立数学模型来描述问题。
2. 把求解的问题分成若干个子问题
3. 对每一子问题求解,得到子问题的局部最优解。
4. 把子问题的解局部最优解合成原来解问题的一个解
算法分析与设计 计算机算法分析与设计论文
实现该算法的过程:
a.从问题的某一初始解出发;
b.while 能朝给定总目标前进一步 do
c.求出可行解的一个解元素;
d.由所有解元素组合成问题的一个可行解。[www.61k.com)
贪心实例大演练
1.用贪心法求解付款问题。
假设有面值为5元、2元、1元、5角、2角、1角的货币,需要找给顾客4元6角现金,为使付出的货币的数量最少,首先选出1张面值不超过4元6角的最大面值的货币,即2元,再选出1张面值不超过2元6角的最大面值的货币,即2元,再选出1张面值不超过6角的最大面值的货币,即5角,再选出1张面值不超过1角的最大面值的货币,即1角,总共付出4张货币
在付款问题每一步的贪心选择中,在不超过应付款金额的条件下,只选择面值最大的货币,而不去考虑在后面看来这种选择是否合理,而且它还不会改变决定:一旦选出了一张货币,就永远选定。付款问题的贪心选择策略是尽可能使付出的货币最快地满足支付要求,其目的是使付出的货币张数最慢地增加,这正体现了贪心法的设计思想。
2.活动安排问题
这个问题指的是一个资源在某个时间点上只能由某个对象独占使用,因此出现了资源争夺的问题。贪心算法在这里主要是解决资源的分配使用问题。贪心算法给出了在一定的时间段上资源给最多个对象使用的一种最优解。
假设有活动集合E={n1,n2,n3...},并且每个活动的开始时间集合定义为S={s1,s2,s3...}结束时间集合定义为F={f1,f2,f3...},那么活动i和活动j的进行时间可以用区间[si,fi),[sj,fj)来表示,当si>=fj或者sj>=fi时我们称为两个活动不冲突,也就是说这两个活动可以被安排分别独占使用资源。贪心算法来解决这个问题的思想是首先根据活动的结束时间将所有活动按升序排序,然后首先设定第一个活动选入可以独占使用资源的活动集合,之后依次比较待选集合当中活动是否与选中集合当中最后一个活动冲突,如果不冲突则选入活动。
算法分析与设计 计算机算法分析与设计论文
整个思想确保了资源的在使用时间最长,并且将得出最多活动使用资源解集当中的一个解。[www.61k.com]具体算法如下:
void arrange(int s[],int f[],bool A[],int n)
{
A[0] = true;
int lastSelected = 0;
for (int i = 1;i < n;i++)
if (s[i] >= f[lastSelected])
{
A[i] = true;
lastSelected = i;
}
else
A[i] = false;
}
这里也有特别需要注意的是地方,我们使用这个算法之前必须将所有的活动按照结束时间做升序排列,否则可能得到最差解。
3.贪心算法解背包
一个旅行者有一个最多能装C公斤重量的背包,已知n个重量和价值分别为ci>0和pi>0(i=1,2,…,n)的物品,选择哪些物品装入背包,可使在背包的容量限制之内所装物品的价值最大,这就是背包问题。0-1背包特点是:每种物品都仅有一件,可以选择放入或不放。
0-1背包问题:给定n种物品和一个背包。物品i的重量是Wi,其价值为Vi,背包的容量为C。应如何选择装入背包的物品,使得装入背包中物品的总价值最大? 在选择装入背包的物品时,对每种物品i只有两种选择,即装入背包为1或不装入背包为0。不能将物品i装入背包多次,也不能只装入部分的物品i。021背包问题的主要特点是在选择物品i装入背包时,每种物品仅有一件,可以选择放或不放。
在求解0-1背包问题时,对贪心算法可以使用一些策略, 使其得到的解更接近最优解。具体方案如下:
(1) 价值优先策略:从剩余的物品中,选取价值最大的可以装入背包的物品。此时,价值最大的优先被装入背包,然后装入下一个价值最大的物品,直到不能再装入剩下的物品为止。
算法分析与设计 计算机算法分析与设计论文
(2) 重量优先策略:从剩余的物品中选取重量最小的物品装入背包中,这种策略一般不能得到最优解。[www.61k.com)
(3) 单位价值优先策略:根据价值/重量的比值,按照每一次选取剩下的物品中比值最大的物品装入背包,直到不能再装入为止。
以上三种策略都不能保证得到最优解,但三种策略相比较而言,第三种策略与最优解相差较小。如果可以选择物品的一部分,用单位价值策略可以保证得到最优解。
在贪心算法时间复杂度的估算中,由于需要对重量或价值或两者的比值进行排序,所以贪心算法的时间复杂度为O(n*logn)。
下面是一种实现过程:
void bagloading(int x[],float p[],float w[],float c,int n)
{
//x[]取值为0或1,x[i]=1当且仅当背包i背装载;
//p[]是物品价值;
//w[]是物品重量;
//c表示背包的容量;
//n表示物品的件数;
float t,k,pw[num];
int i,j,m,kk;
for(i=0;i<n;i++)
pw[i]=p[i]/w[i];
//对各个点的坐标按由大到小进行排序(使用改进的冒泡排序)
m=n-1;
while (m>0)
{
kk=0;
for(j=0;j<m;j++)
if (pw[j]<pw[j+1])
{
算法分析与设计 计算机算法分析与设计论文
t=p[j];
p[j]=p[j+1]; p[j+1]=t;
k=w[j];
w[j]=w[j+1]; w[j+1]=k;
kk=j;
}
m=kk;
}
//按p/w次序从大到小选择物品 i=0;
while(i<n&&(w[i]<=c)) {
x[i]=1;
c-=w[i];
i++;
}
}
int main()
{
int n,all;
float c,p1,w1;
float p[num];
float w[num];
int x[num];
int i;
cout<<"请输入物品的件数:"; cin>>n;
cout<<"请输入背包的最大容量:";
算法分析与设计 计算机算法分析与设计论文
cin>>c;
cout<<"请依次输入各物品的价值与重量 \n每个物品的价值与重量之间用空格隔开,回车后输入另一个物品:"<<endl;
//通过键盘依次输入各物品的价值与重量
for(i=0;i<n;i++)
{
cin>>p[i]>>w[i];
}
//调用函数
bagloading(x,p,w,c,n);
//统计物品的总价值、总重量以及件数并输出
//统计装入物品的价值及重量并输出
all=0;
p1=0.0;
w1=0.0;
for(i=0;i<n;i++)
if(x[i]==1)
{
all++;
p1=p1+p[i];
w1=w1+w[i];
}
cout<<endl;
cout<<"所装物品总的价值为:"<<p1<<endl;
cout<<"所装物品总的重量为:"<<w1<<endl;
if (all>0)
{
cout<<"该背包共装入的这"<<all<<"件物品的价值与重量分别为:"<<endl;
for(i=0;i<n;i++)
if(x[i]==1)
算法分析与设计 计算机算法分析与设计论文
cout<<p[i]<<" "<<w[i]<<endl;
}
system("pause");
return 0;
}
分析:
约束条件是装入的物品总重量不超过背包容量:∑wi<=M( M=150)
(1)根据贪心的策略,每次挑选价值最大的物品装入背包,得到的
结果是否最优
(2)每次挑选所占重量最小的物品装入是否能得到最优解
(3)每次选取单位重量价值最大的物品,成为解本题的策略。(www.61k.com)
值得注意的是,贪心算法并不是完全不可以使用,贪心策略一旦经过证明成立后,它就是一种高效的算法,贪心算法还是很常见的算法之一,这是由于它简单易行,构造贪心策略不是很困难,可惜的是,它需要证明后才能真正运用到题目的算法中。
一般来说,贪心算法的证明围绕着:整个问题的最优解一定由在贪心策略中存在的子问题的最优解得来的。
解释如下:
(1) 贪心策略:选取价值最大者。
反例:
W=30
物品:A B C
重量:28 12 12
算法分析与设计 计算机算法分析与设计论文
价值:30 20 20
根据策略,首先选取物品A,接下来就无法再选取了,可是,选取B、C则更好。(www.61k.com)
(2)贪心策略:选取重量最小。它的反例与第一种策略的反例差不多。
(3)贪心策略:选取单位重量价值最大的物品。
反例:
W=30
物品:A B C
重量:28 20 10
价值:28 20 10
根据策略,三种物品单位重量价值一样,程序无法依据现有策略作出判断,如果选择A,则答案错误。
对于选取单位重量价值最大的物品这个策略,可以再加一条优化的规则:对于单位重量价值一样的,则优先选择重量小的!这样,上面的反例就解决了。
当然,本题是个DP问题,用贪心法并不一定可以求得最优解,但毕竟用贪心算法是一种高效的算法。其实动态规划算法是解决这个问题最好的方法,但并不是最快的。
4 总结
通过以上三个实例,我们可以感受到贪心算法的好处简单的总结
算法分析与设计 计算机算法分析与设计论文
一下贪心算法的
在写论文的过程中,我上网查询了很多资料,并且也参考了书本里的内容,通过这些我对算法分析设计又有了进一步的了解,对算法的复杂度也有了新的认识。(www.61k.com)对于我们常用的动态规划算法、回溯法、分支限界法、贪心算法等的思想有了进一步的了解,我相信这对我以后的学习是非常有用的。虽然这门课程已经结束了,但是我所掌握的却很少,因此在接下来的时间里我还会继续学习算法分析与设计,从而能够运用这些算法解决更多的问题。
参考文献:
[ 1 ]王晓东.计算机算法设计与分析(第3版) 电子工业出版社, 2009.
[ 2 ]应莉 0-1背包问题及其算法 计算机与现代化 (2009)06-0024-03
[ 3 ]徐颖 回溯法在0-1背包问题中的应用 软件导刊(2008)12-0054-02
二 : 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归
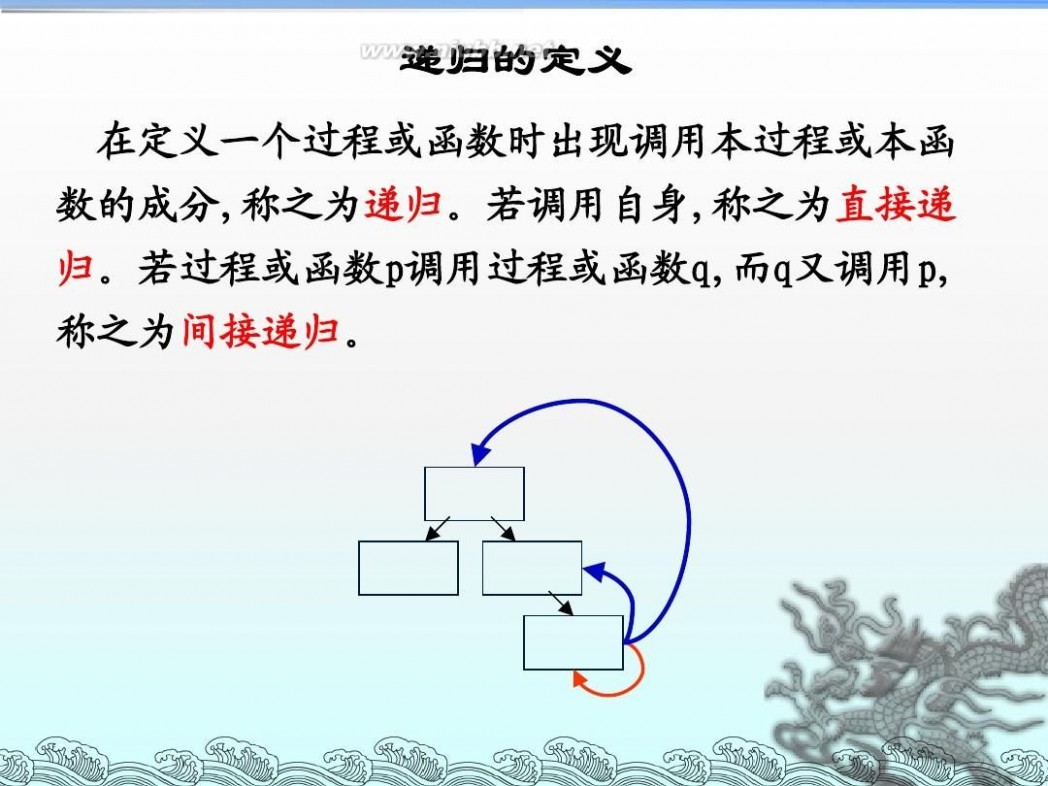
递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归
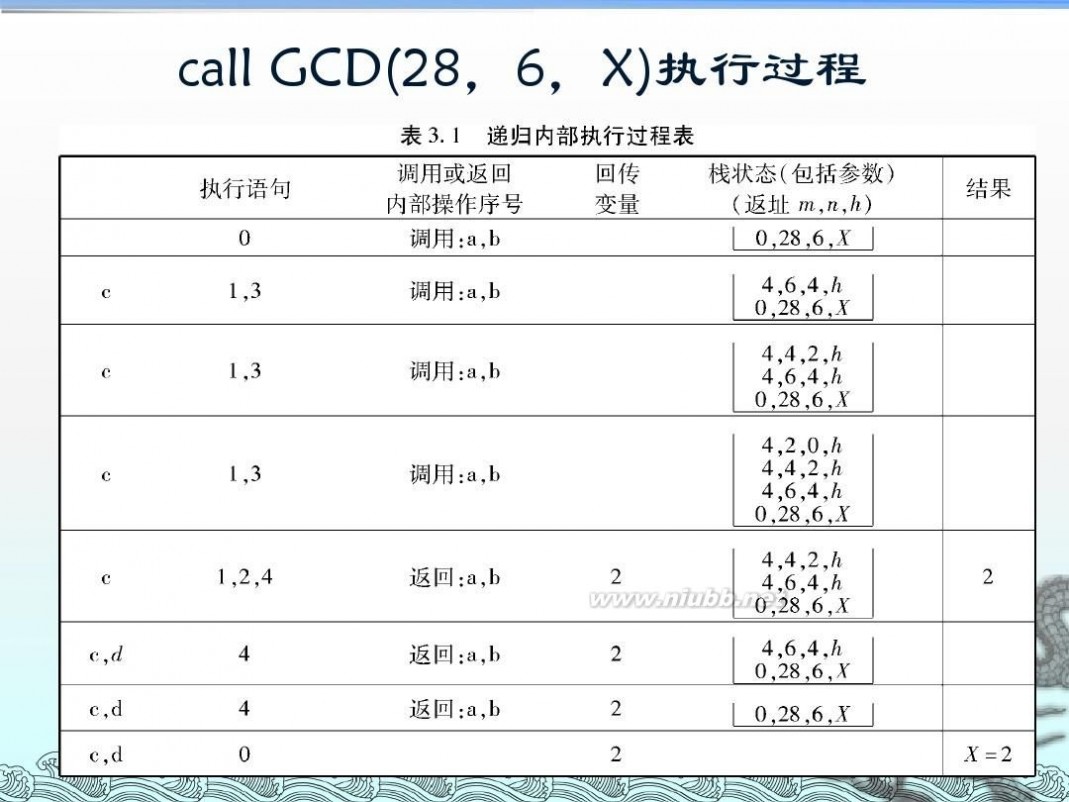
递归算法流程图 算法设计与分析--递归
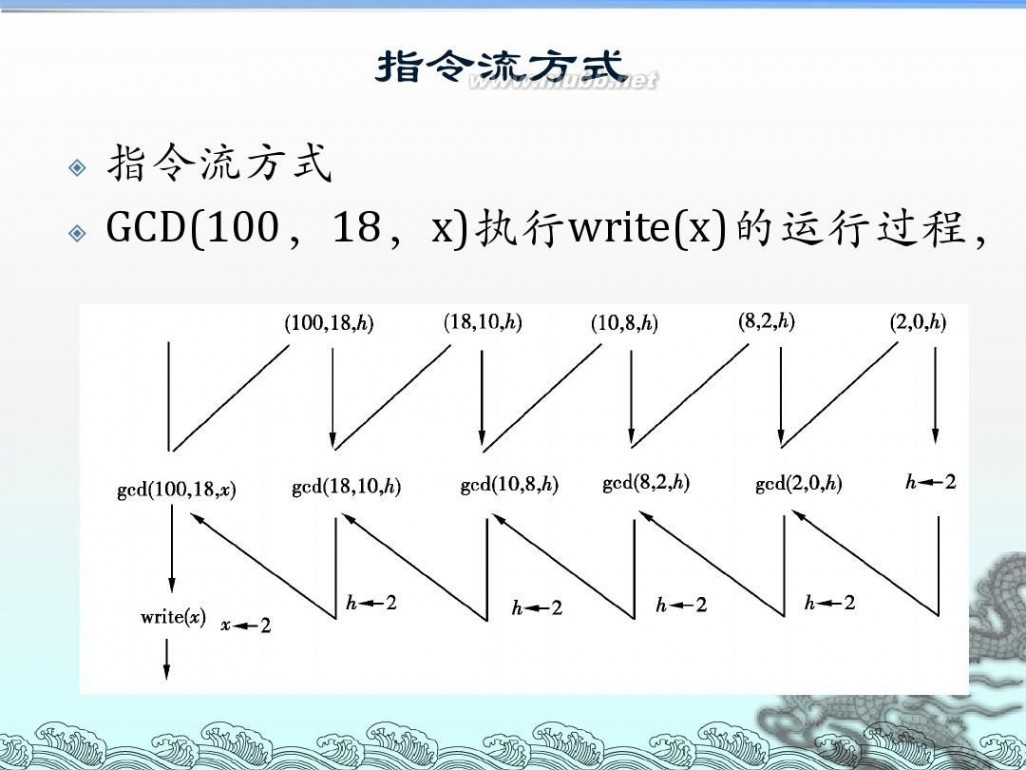
递归算法流程图 算法设计与分析--递归
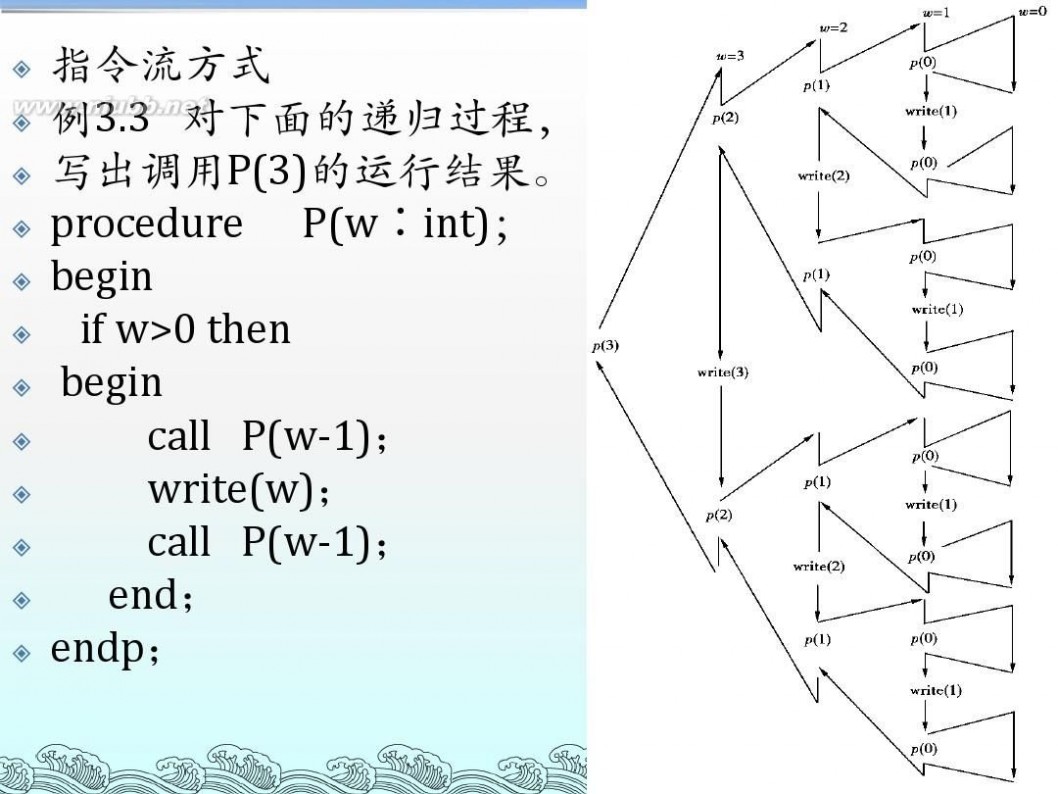
递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归
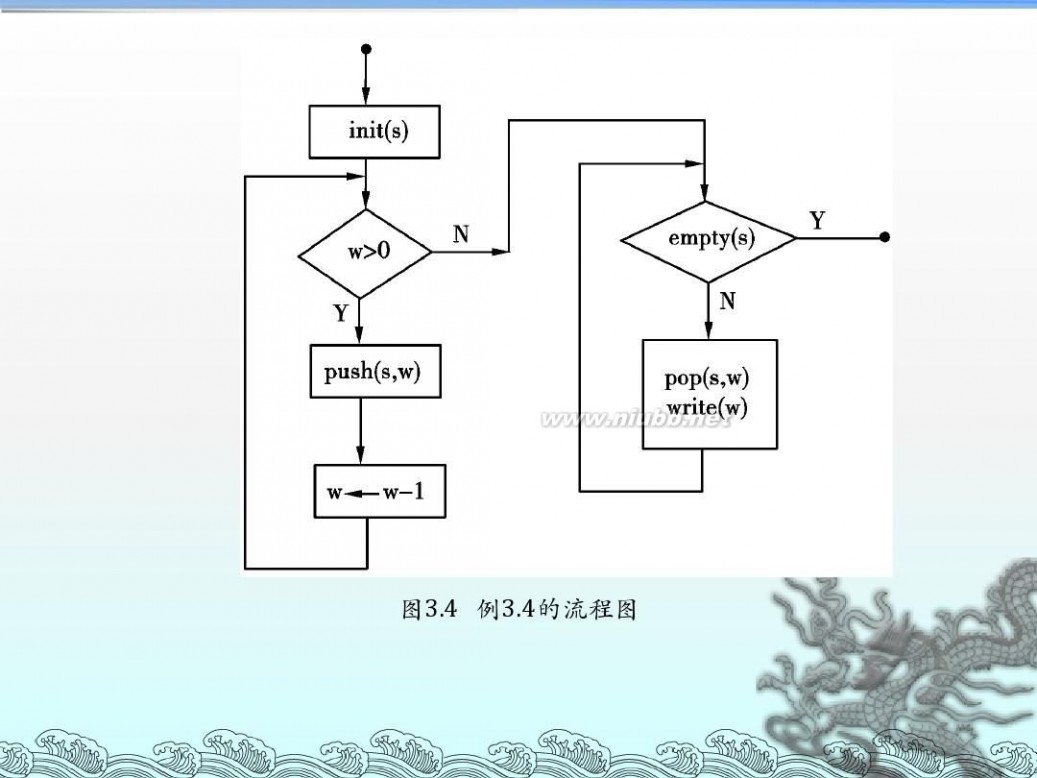
递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归
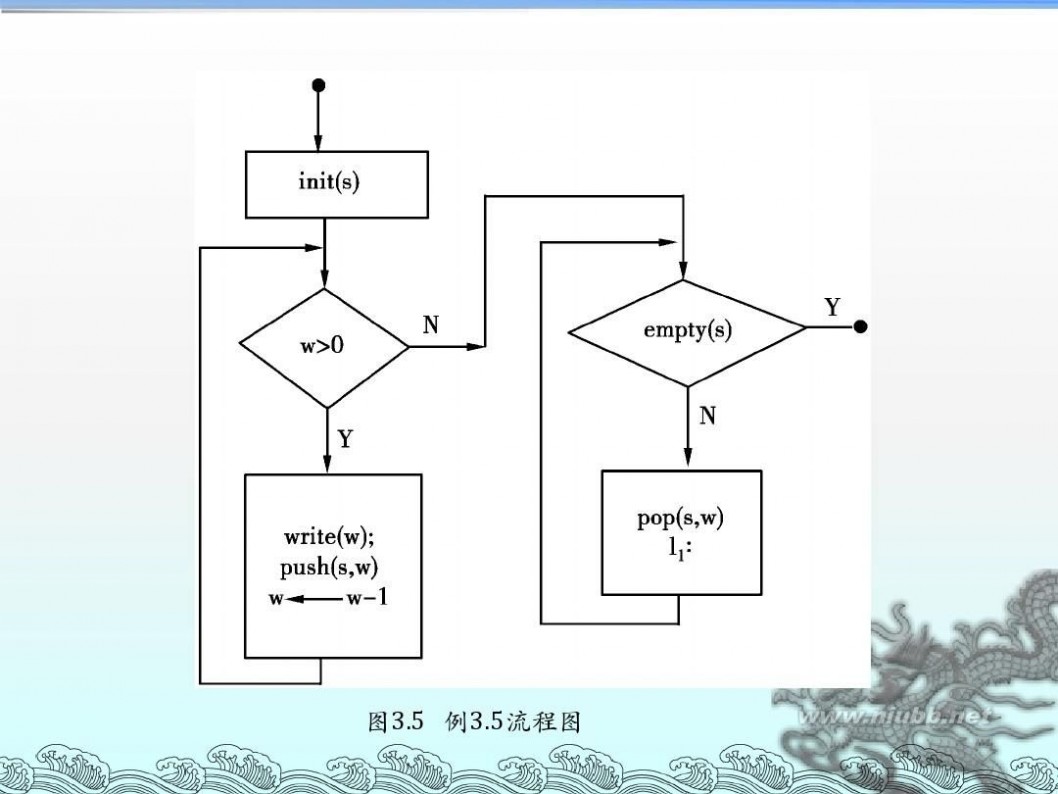
递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归
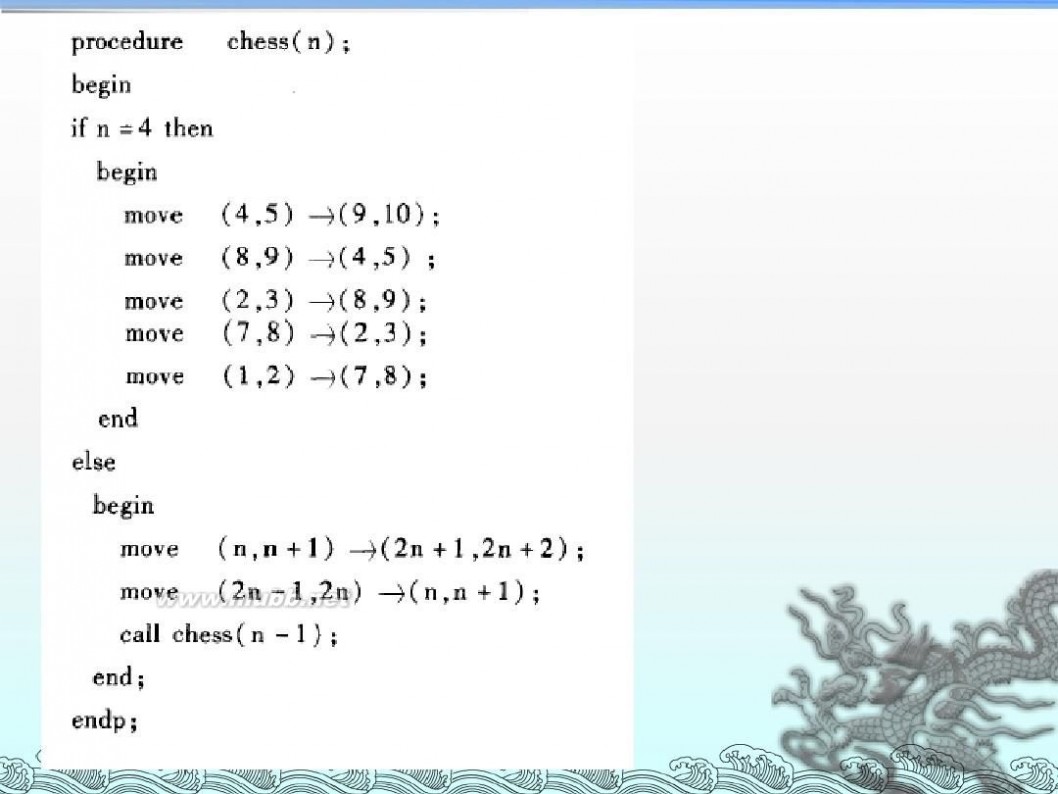
递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归
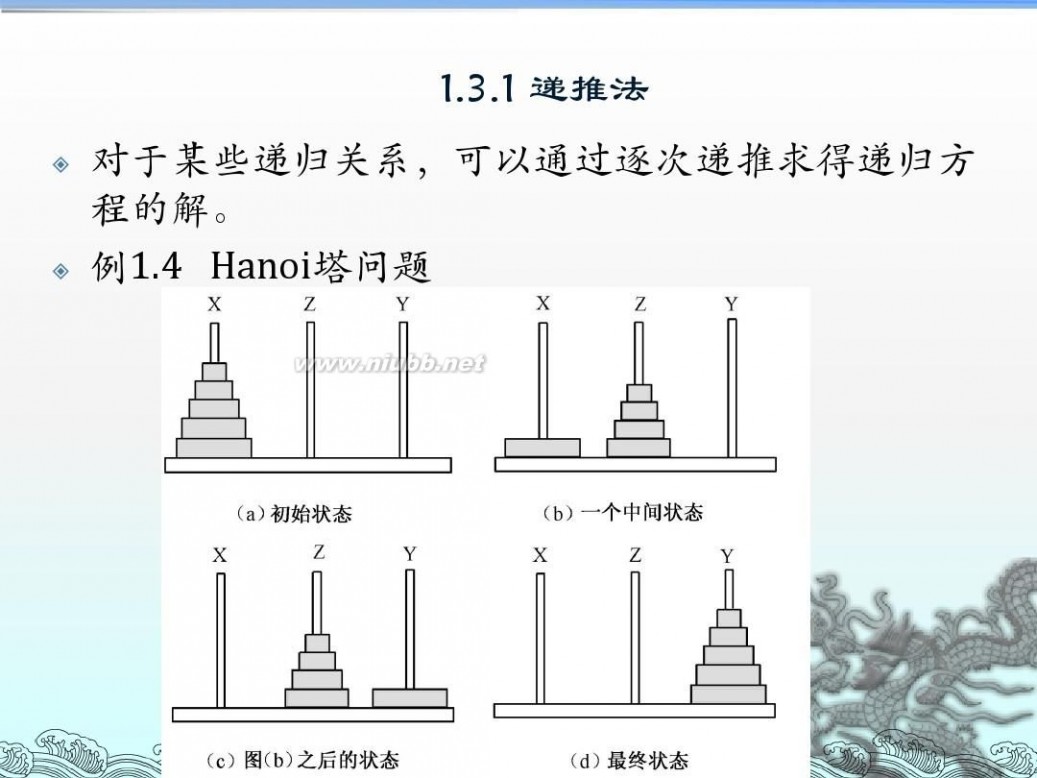
递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

递归算法流程图 算法设计与分析--递归

三 : 算法设计之分治法(1)
引言
说到分治算法,最容易想到的例子是在数组中查找元素,常用的算法是遍历整个数组进行查找,算法时间复杂度为O(n);但是对于有序数组,使用二分查找法,可以使时间复杂度减少到O(logn)。
普通查找法:
int IsElement(int a[], int len, int x)//判断数据x是否为数组a的元素,如果是返回该元素的下标,否则返回-1
{
inti;
for(i=0; i<len; i++)
{
if (a[i] == x)
returni;
}
return-1;
}
二分查找法:
int IsElement(int a[], int len, int x)
{
int left= 0;
intright = len - 1;
intmid;
while(left <= right)
{
mid = (left + right) / 2;//寻找中点,以便将数组分成两半
if (a[mid] == x)//刚好找到
return mid;
else if (a[mid] > x)//比中点元素小,右边界左移
right = mid - 1;
else //否则左边界右移
left = mid + 1;
}
return-1;
}
也可以写成递归的形式:
int IsElement(int a[], int len, intx)//驱动程序
{
returnBinary(a, 0, len-1, x);
}
int Binary(int a[], int left, int right, intx)//二分递归查找
{
int mid= (left+right)/2;
if (left> right)//没找到
return -1;
if(a[mid] == x) //刚好找到
return mid;
else if(a[mid] > x) //比中点元素小,递归查找左侧数组
return Binary(a, left, mid-1, x);
else//比中点元素大,递归查找右侧数组
return Binary(a, mid+1, right, x);
}
在二分查找法中,我们不断的减少查找区域的范围,把大问题分解成结构相同的小问题,直到问题得解。与二分查找法类似的算法很多,我们将它们归类称为分治法。
设计原理
1.分治法的基本思想
任何一个可以用计算机求解的问题所需的计算时间都与其规模N有关。问题的规模越小,越容易直接求解,解题所需的计算时间也越少。例如,对于n个元素的排序问题,当n=1时,不需任何计算;n=2时,只要作一次比较即可排好序;n=3时只要作3次比较即可,…。而当n较大时,问题就不那么容易处理了。要想直接解决一个规模较大的问题,有时是相当困难的。
分治法的设计思想是:将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。如果原问题可分割成k个子问题,1<k≤n,且这些子问题都可解,并可利用这些子问题的解求出原问题的解,那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小模式,这就为使用递归技术提供了方便。在这种情况下,反复应用分治手段,可以使子问题与原问题类型一致而其规模却不断缩小,最终使子问题缩小到很容易直接求出其解。
通常,这种分析方法的基本点在于“分解”,因此这种方法也被称为“划分(Divide)和解决(Con—quer)”方法。也正因为如此,它和语言工具中的递归结下了不解之缘。分治与递归像一对孪生兄弟,经常同时应用在算法设计之中,并由此产生许多高效算法。
2.分治法的适用条件
分治法所能解决的问题一般具有以下几个特征:
(1)该问题的规模缩小到一定的程度就可以容易地解决;
(2)该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质;
(3)利用该问题分解出的子问题的解可以合并为该问题的解;
(4)该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。
上述的第一条特征是绝大多数问题都可以满足的,因为问题的计算复杂性一般是随着问题规模的增加而增加;第二条特征是应用分治法的前提,它也是大多数问题可以满足的,此特征反映了递归思想的应用;第三条特征是关键,能否利用分治法完全取决于问题是否具有第三条特征,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑贪心法或动态规划法。第四条特征涉及到分治法的效率,如果各子问题是不独立的,则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然可用分治法,但一般用动态规划法较好。
3.分治法的基本步骤
分治法在每一层递归上都有三个步骤:
分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题;
解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题;
合并:将各个子问题的解合并为原问题的解。
它的一般的算法设计模式如下:
DividAndConquer(p(n))//分治法设计原理
{
if (n<= n0)
return Adhoc(p(n));
else
{
//将P分解为较小的子问题P1、P2、…、Pk
Divide p int o smaller subinstances P1, P2, ..., Pk;
for (i=1; i<=k; i++)
yi = DividAndConquer(pi);//递归解决Pi
return Merge(y1, y2, ..., yk);//合并子问题
}
}
其中p(n)表示一个规模为n的问题P,可以把它分解成k个规模较小的子问题,这些问题相互独立,并且与原来的问题结构相同。在解决这些子问题时,又用相同的方式对每一个子问题进行进一步的分解,直到某个阈值n0为止。递归的解这些子问题,再把各个子问题的解合并起来,就得到原来问题的解。这就是分治法的思想方法。n0为一阈值,表示当问题P的规模不超过n0时,问题已容易直接解出,不必再继续分解。Adhoc(p(n))是该分治法中的基本子算法,用于直接解小规模的问题P。因此,当P的规模不超过n0时,直接用算法Adh(www.61k.com)oc(p(n))求解。经典示例
例1最大最小问题:老板有一袋金块,共n块。将有两名最优秀的雇员每人得到其中的一块,排名第一的得到最重的那块,排名第二的雇员得到袋子中最轻的金块。假设有一台比较重量的仪器,我们希望用最少的比较次数找出最重和最轻的金块。
算法分析:这个问题可以转化一个具有n个元素的数组里,寻找最大和最小元素问题。
一般算法是遍历数组,依次将每个元素和当前最大,最小值判断,直至遍历数组结束,返回最大,最小值。
void MaxMin(int a[], int n, int *max, int*min)
{
int i =0;
*max =*min = a[0];
for(i=1; i<n; i++)
{
if (a[i] < *min)
*min = a[i];
if (a[i] > *max)
*max = a[i];
}
}
很清楚,在输入规模为n时,这个算法所执行的元素比较次数是2n-2。用分治法可以较少比较次数地解决上述问题:
如果集合中只有1个元素,则它既是最大值也是最小值;
如果有2个元素,则一次Max(i,j),一次Min(i,j)就可以得到最大值和最小值;
如果有多于2个元素,则把集合分成两个规模相当子集合,递归的应用这个算法分别求出两个子集合的最大值和最小值,最后让子集合1的最大值跟子集合2的最大值比较得到整个集合的最大值;让子集合1的最小值跟子集合2的最小值比较得到整个集合的最小值。
void MaxMin2(int a[], int left, int right, int*max, int *min)
{
int x1, x2, y1, y2;
intmid;
if((right-left) <= 1)//相等或相邻
{
if (a[right] > a[left])
{
*max = a[right];
*min = a[left];
}
else
{
*max = a[left];
*min = a[right];
}
}
else
{
mid = (left + right) / 2;
MaxMin2(a, left, mid, &x1, &y1);//把数组分成两个规模相当子数组递归
MaxMin2(a, mid+1, right, &x2,&y2);
*max = (x1 > x2) ? x1 : x2;
*min = (y1 < y2) ? y1 : y2;
}
}
使用分治法法后可以把元素比较次数从原来的2n-2减少为(3n/2)- 2。
例2 二分法求方程近似解:求方程f(x) = x^3 +x^2 - 1 = 0在[0,1]上的近似解,精确度为0.01。
算法分析:二分法求方程近似解的基本思想:将方程的有解区间平分为两个小区间,然后判断解在哪个小区间;继续把有解的区间一分为二进行判断,如此周而复始,直到求出满足精确要求的近似解。
二分法求方程近似解的算法步骤:
⑴确定区间[a,b],验证f(a).f(b) <0,给定精确度e
⑵求区间(a, b)的中点mid
⑶计算f(mid)
若f(mid) = 0,则mid就是函数的零点
若f(a).f(mid) < 0,则令b = mid(此时零点a< x0 < mid)
若f(mid).f(b) < 0,则令a = mid(此时零点mid< x0 < b)
⑷判断是否达到精确度e:即若|a-b| <e,则得到零点近似值a(或b);否则重复⑵-⑷。
代码如下:
double F(double a, double b, double c, double d,double x)//函数表达式
{
return (((a * x + b) * x) * x + d) /c;
}
double Function(double a, double b, double c,double d, double low, double high, double e)
{
doublemid = (low + high) / 2;
if (F(a,b, c, d, mid) == 0)
return mid;
while((high-low) >= e)
{
mid = (low + high) / 2;
if (F(a, b, c, d, mid) == 0)
return mid;
if (F(a, b, c, d, low)*F(a, b, c, d, mid) <0)
high = mid;
else
low = mid;
}
returnlow;
}
例3二分法插入排序:插入排序是经典的简单排序法,它的时间复杂度最坏为O(n^2)。代码如下:
//插入法对数组进行排序,从第二个元素开始,依次把元素插入到其左边比其小的元素之后
void InsertSort(int a[], int len)
{
int i,j, temp;
for(i=1; i<len; i++)//从第二个元素开始,依次从左向右判断
{
temp = a[i]; //记录当前被判断的元素
j = i - 1;
while (j >= 0 &&a[j] > temp)//把比temp大的元素向后移动一个位置
{
a[j+1] =a[j];
j--;
}
a[j+1] = temp;//把temp插入到适当位置
}
}
插入算法的原理是总是使得当前被插入的元素左侧的数组是已经排好序的。在上面的算法中我们是采用遍历a[i]左侧数组的方法来查找插入位置,而实际上我们完全可以根据二分查找的原理,来实现二分法插入排序。
算法思想简单描述:在插入第i个元素时,对前面的0~i-1元素进行折半,先跟他们中间的那个元素比,如果小,则对前半再进行折半,否则对后半进行折半,直到low>high,然后再把第i个元素前与目标位置之间的所有元素后移,再把第i个元素放在目标位置上。代码如下:
void HalfInsertSort(int a[], int len)
{
int i, j;
int low, high, mid;
int temp;
for (i=1; i<len; i++)
{
temp = a[i];
low = 0;
high = i - 1;
while (low <= high)//在a[low。。。high]中折半查找有序插入的位置
{
mid = (low + high) / 2;
if (a[mid] > temp)
high = mid - 1;
else
low= mid + 1;
} //while
for (j=i-1; j>high; j--)//元素后移
a[j+1] = a[j];
a[high+1] = temp; //插入
}//for
}
排序的算法很多,其中多数都要用到分治的思想,如希尔排序,合并排序和快速排序等,这里不再一一叙述,感兴趣的读者可以到我的BLOG查看:
http://blog.programfan.com/blog.asp?blogid=96&columnid=2071
例4找出伪币:给你一个装有16个硬币的袋子。16个硬币中有一个是伪造的,并且那个伪造的硬币比真的硬币要轻一些。你的任务是找出这个伪造的硬币。为了帮助你完成这一任务,将提供一台可用来比较两组硬币重量的仪器,利用这台仪器,可以知道两组硬币的重量是否相同。比较硬币1与硬币2的重量。假如硬币1比硬币2轻,则硬币1是伪造的;假如硬币2比硬币1轻,则硬币2是伪造的。这样就完成了任务。假如两硬币重量相等,则比较硬币3和硬币4。同样,假如有一个硬币轻一些,则寻找伪币的任务完成。假如两硬币重量相等,则继续比较硬币5和硬币6。按照这种方式,可以最多通过8次比较来判断伪币的存在并找出这一伪币。但是很明显,这样的效率实在太低,请设计一种方法,使得比较的次数最少。
算法分析:利用分而治之方法。假如把16硬币的例子看成一个大的问题。第一步,把这一问题分成两个小问题。随机选择8个硬币作为第一组称为A组,剩下的8个硬币作为第二组称为B组。这样,就把16个硬币的问题分成两个8硬币的问题来解决。第二步,判断A和B组中是否有伪币。可以利用仪器来比较A组硬币和B组硬币的重量。假如两组硬币重量相等,则可以判断伪币不存在。假如两组硬币重量不相等,则存在伪币,并且可以判断它位于较轻的那一组硬币中。最后,在第三步中,用第二步的结果得出原先16个硬币问题的答案。若仅仅判断硬币是否存在,则第三步非常简单。无论A组还是B组中有伪币,都可以推断这16个硬币中存在伪币。因此,仅仅通过一次重量的比较,就可以判断伪币是否存在。
现在假设需要识别出这一伪币。把两个或三个硬币的情况作为不可再分的小问题,注意如果只有一个硬币,那么不能判断出它是否就是伪币。(在本题中n=2^4,所以不可能出现一个或三个硬币一组的情况)在一个小问题中,通过将一个硬币分别与其他两个硬币比较,最多比较两次就可以找到伪币。这样,16硬币的问题就被分为两个8硬币(A组和B组)的问题。通过比较这两组硬币的重量,可以判断伪币是否存在。如果没有伪币,则算法终止。否则,继续划分这两组硬币来寻找伪币。假设B是轻的那一组,因此再把它分成两组,每组有4个硬币。称其中一组为B1,另一组为B2。比较这两组,肯定有一组轻一些。如果B1轻,则伪币在B1中,再将B1又分成两组,每组有两个硬币,称其中一组为B1a,另一组为B1b。比较这两组,可以得到一个较轻的组。由于这个组只有两个硬币,因此不必再细分。比较组中两个硬币的重量,可以立即知道哪一个硬币轻一些。较轻的硬币就是所要找的伪币。
int FalseCoin(int a[], int left, intright)
{
int mid= (left + right) / 2;
int sum1= 0, sum2 = 0;
inti;
if((right-left) ==1)//只有两枚硬币,轻者为伪币,等重则无伪币
return (a[left] < a[right]) ? left : (a[left]> a[right]) ? right : -1;
//多于两枚硬币,将数组分成两半,分而治之
for(i=left; i<=mid; i++)
sum1 += a[i];
for(i=mid+1; i<=right; i++)
sum2 +=a[i];
if (sum1== sum2)//等重则无伪币
return -1;
else if(sum1 < sum2)
return FalseCoin(a, left, mid);
else
return FalseCoin(a, mid+1, right);
}
在上述算法中我们每次把硬币分成两组,解决16个硬币问题,需要比较的次数为4次。如果我们每次把硬币分成4组,需要的平均比较次数会减少为3次。代码如下;
int FalseCoin(int a[], int len, int left, intright)
{
intleft1, right1, left2, right2, left3, right3, left4,right4;
intsum1, sum2, sum3, sum4;
int q,i;
if(right == left)//如果子数组只有一枚硬币,将其与相邻的硬币比较
{
if (left > 0)
return (a[left]<a[left-1]) ? left :(a[left]>a[left-1]) ? left-1 : -1;
if (right < len-1)
return (a[right]<a[right+1]) ? right :(a[right]>a[right+1]) ? right-1 : -1;
return-1;
}
if((right-left) ==1)//如果子数组只有两枚硬币,轻者为伪币,等重则无伪币
{
return (a[left] < a[right]) ? left : (a[left]> a[right]) ? right : -1;
}
//将硬币分成4等份
q =(right - left + 1) / 4;
left1 =left;
right1 =left1 + q - 1;
left2 =right1 + 1;
right2 =left2 + q - 1;
left3 =right2 + 1;
right3 =left3 + q - 1;
left4 =right3 + 1;
right4 =left4 + q - 1;
//累计每组硬币的重量
sum1 =sum2 = sum3 = sum4 = 0;
for(i=left1; i<=right1; i++)
sum1 += a[i];
for(i=left2; i<=right2; i++)
sum2 += a[i];
for(i=left3; i<=right3; i++)
sum3 += a[i];
for(i=left4; i<=right4; i++)
sum4 += a[i];
//将硬币两两比较
if (sum1!= sum2)//伪币在第1,2组硬币中
{
if (sum1 < sum2)
return FalseCoin(a, len, left1, right1);
else
return FalseCoin(a, len, left2, right2);
}
if (sum3!= sum4)//伪币在第3,4组硬币中
{
if (sum3 < sum4)
return FalseCoin(a, len, left3, right3);
else
return FalseCoin(a, len, left4, right4);
}
}
本文标题:算法分析与设计-计算机算法分析与设计论文61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1