一 : 第四章、人工神经元网络模型

第四章 人工神经元网络模型
第一节 引言 人工神经网络就是模拟人脑细胞的分布式工作特点和 自组织功能实现并行处理、自学习和非线性映射等能力。 神经网络：高度复杂的非线性动力学系统， 特点：快速并行处理能力和自学习能力。 发展： 1943：McCulloch和Pitts MP模型(神经元数学模型) 1944：Hebb Hebb规则(神经元连接强度的学习算法) 1957：Rosenblatt 感知器(Perceptron)模型(完整的人工神 经网络，有感知和学习能力) 1976：Grossberg 自适应共振理论ART(Adaptive Resonance Theory)

1982：Hopfield HNN模型（Hopfield Neural Networks） 1986：Rumelhart BP算法（back propagation） 误差反向传播学习算法 神经元网络系统主要研究三个方面的内容： 线性 处理单元 神经元模型 非线性 前向网络(BP) 反馈网络(Hopfield) 自组织网络(ART) 有 无 学习：神经元系统根据某种学习方法调整它内部参数以完 成特定的任务的过程。 神经网络学习方法 导师指导

神经网络结构

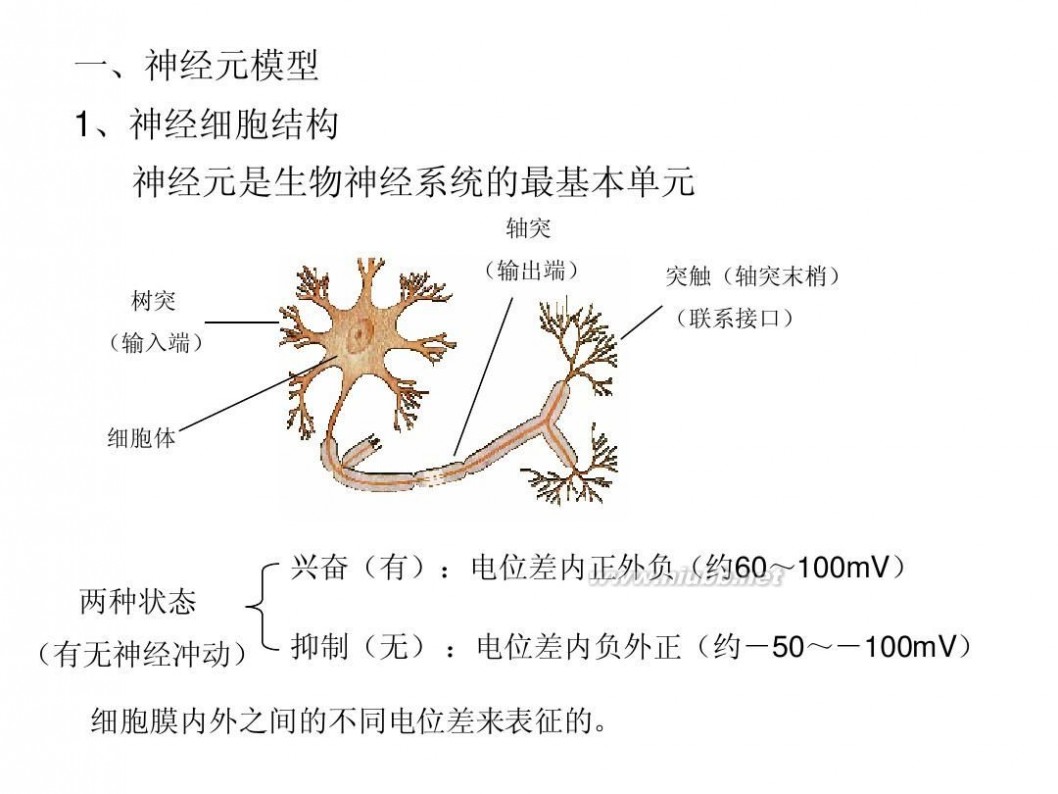
一、神经元模型 1、神经细胞结构 神经元是生物神经系统的最基本单元
轴突 （输出端） 树突 （输入端） 突触（轴突末梢） （联系接口）

细胞体

兴奋（有）：电位差内正外负（约60～100mV） 两种状态 （有无神经冲动） 抑制（无） ：电位差内负外正（约－50～－100mV）

细胞膜内外之间的不同电位差来表征的。

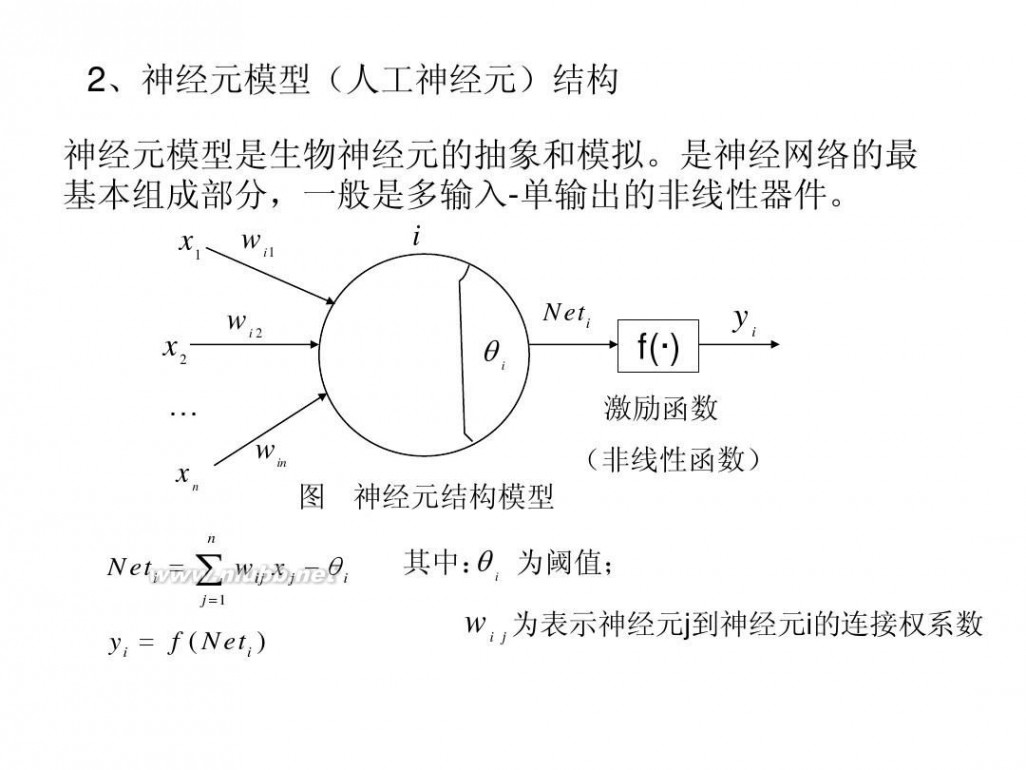
2、神经元模型（人工神经元）结构 神经元模型是生物神经元的抽象和模拟。是神经网络的最 基本组成部分，一般是多输入-单输出的非线性器件。 i x1 wi1

x2
…

wi 2

θi

Neti 　

f(·)
激励函数

yi

xn
n

win
图 神经元结构模型

（非线性函数） 其中： i 为阈值； θ

Neti = ∑ wij x j ? θ i
j =1

yi = f ( Neti )

wi j 为表示神经元j到神经元i的连接权系数

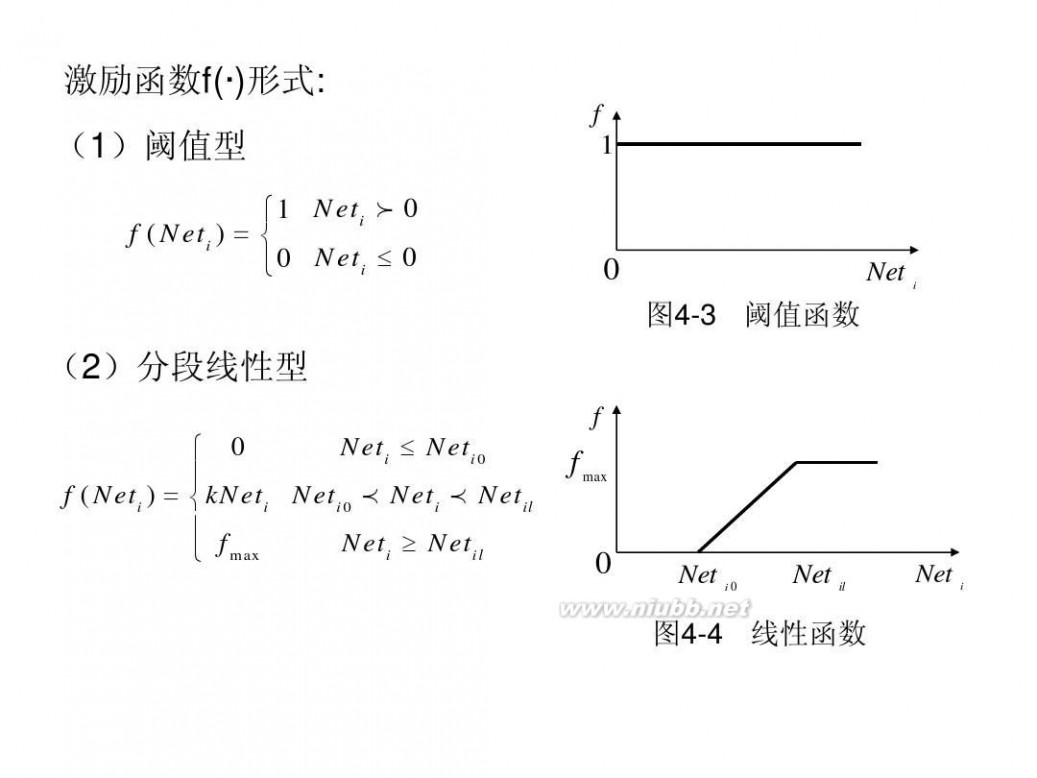
激励函数f(·)形式: （1）阈值型
?1 Neti f 0 f ( Neti ) = ? ?0 Neti ≤ 0
f 1

0
图4-3 阈值函数

Neti

（2）分段线性型
Neti ≤ Neti 0 ? 0 ? f ( Neti ) = ?kNeti Neti 0 p Neti p Netil ? f Neti ≥ Netil ? max
f

f max

0

Neti 0

Netil

Neti

图4-4 线性函数

f
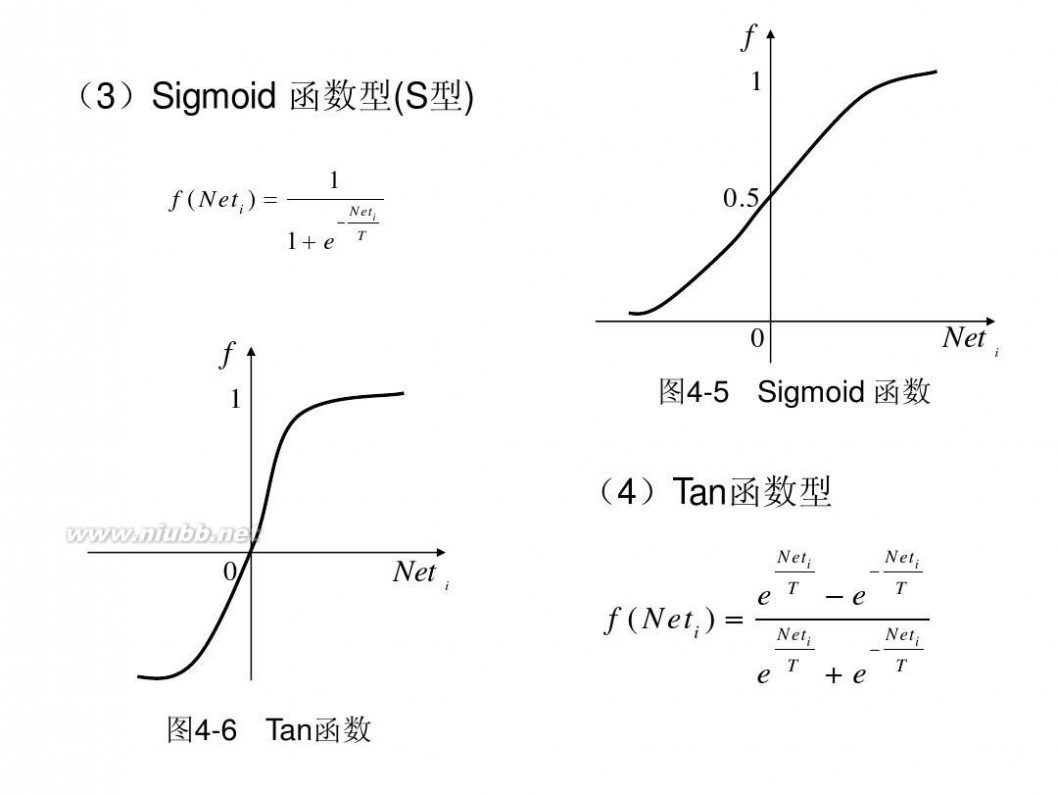
（3）Sigmoid 函数型(S型)
f ( Neti ) = 1 1+ e
? Neti T

1

0.5

f
1

0
图4-5 Sigmoid 函数

Neti

（4）Tan函数型
0

Neti

f ( Neti ) =

e e

Neti T Neti T

?e +e

? ?

Neti T Neti T

图4-6 Tan函数

二、神经网络的模型分类 按层次： （1）神经元层次模型：只是研究单一神经元的动态特性和 自适应特性，探索神经元对输入信息的处理和存储能力。 （2）组合式模型 这种模型是由数种相互补充、相互协作的 神经元组成，用于完成某些特定的任务。 （3）网络层次模型 它是由众多相同神经元相互连接而成 的网络，着重研究神经网络的整体性能。 （4）神经系统层次模型 一般由多个不

同性质的神经网络 构成，以模拟生物神经系统更复杂、更抽象的特性。

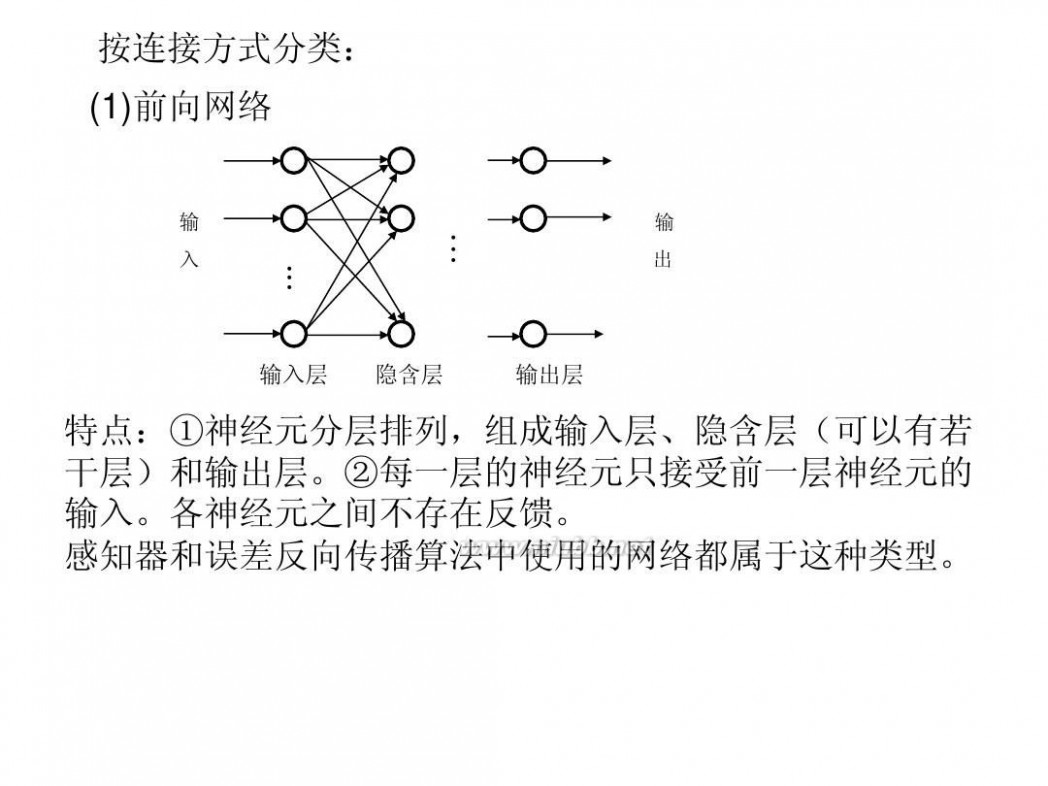
按连接方式分类： (1)前向网络
输 入
输 出

M
输入层 隐含层

M
输出层

特点：①神经元分层排列，组成输入层、隐含层（可以有若 干层）和输出层。②每一层的神经元只接受前一层神经元的 输入。各神经元之间不存在反馈。 感知器和误差反向传播算法中使用的网络都属于这种类型。

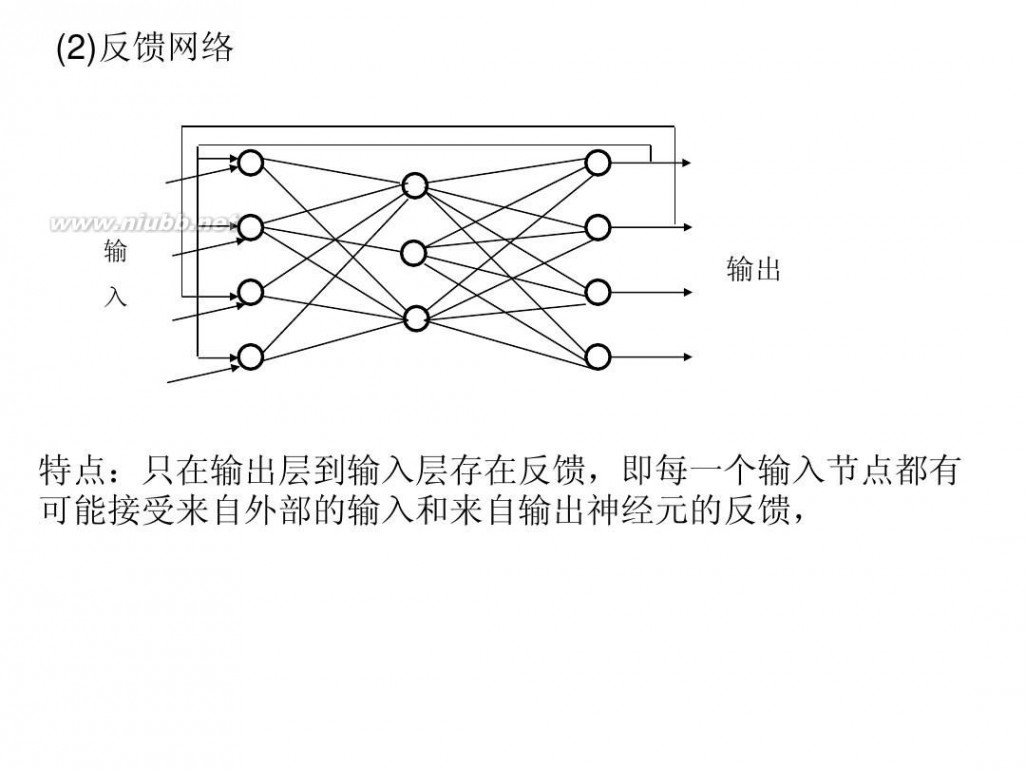
(2)反馈网络

输 入

输出

特点：只在输出层到输入层存在反馈，即每一个输入节点都有 可能接受来自外部的输入和来自输出神经元的反馈，

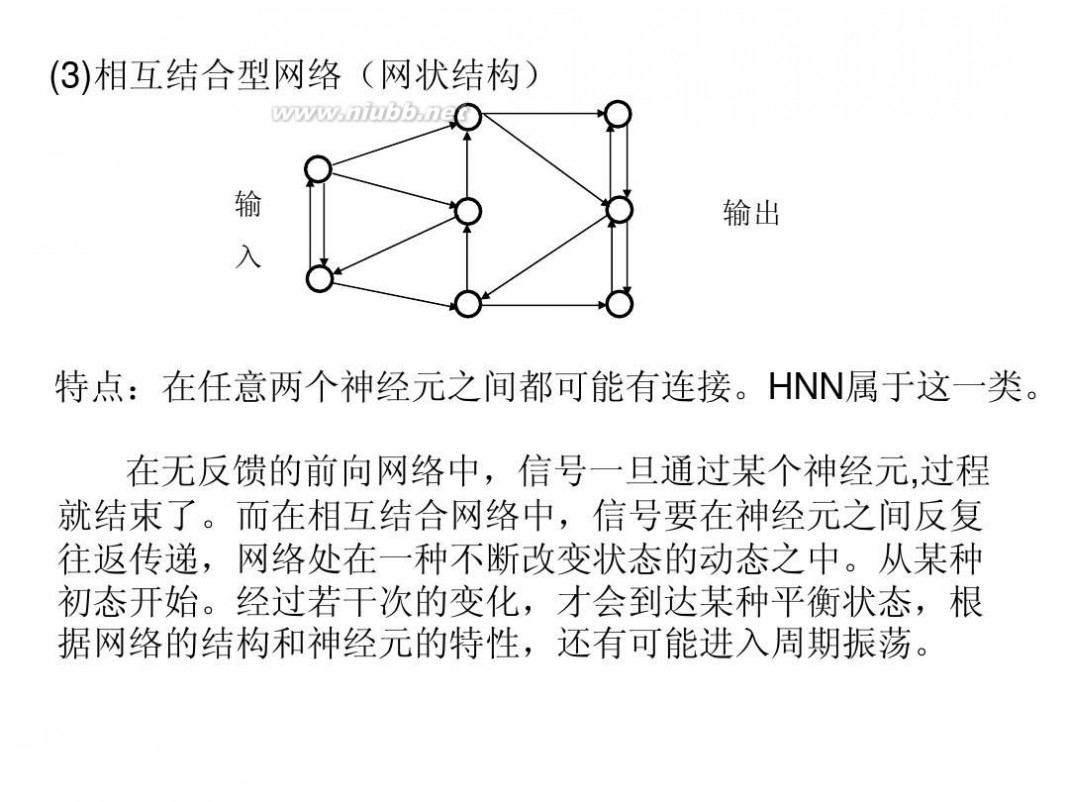
(3)相互结合型网络（网状结构）

输 入

输出

特点：在任意两个神经元之间都可能有连接。HNN属于这一类。 在无反馈的前向网络中，信号一旦通过某个神经元,过程 就结束了。而在相互结合网络中，信号要在神经元之间反复 往返传递，网络处在一种不断改变状态的动态之中。从某种 初态开始。经过若干次的变化，才会到达某种平衡状态，根 据网络的结构和神经元的特性，还有可能进入周期振荡。

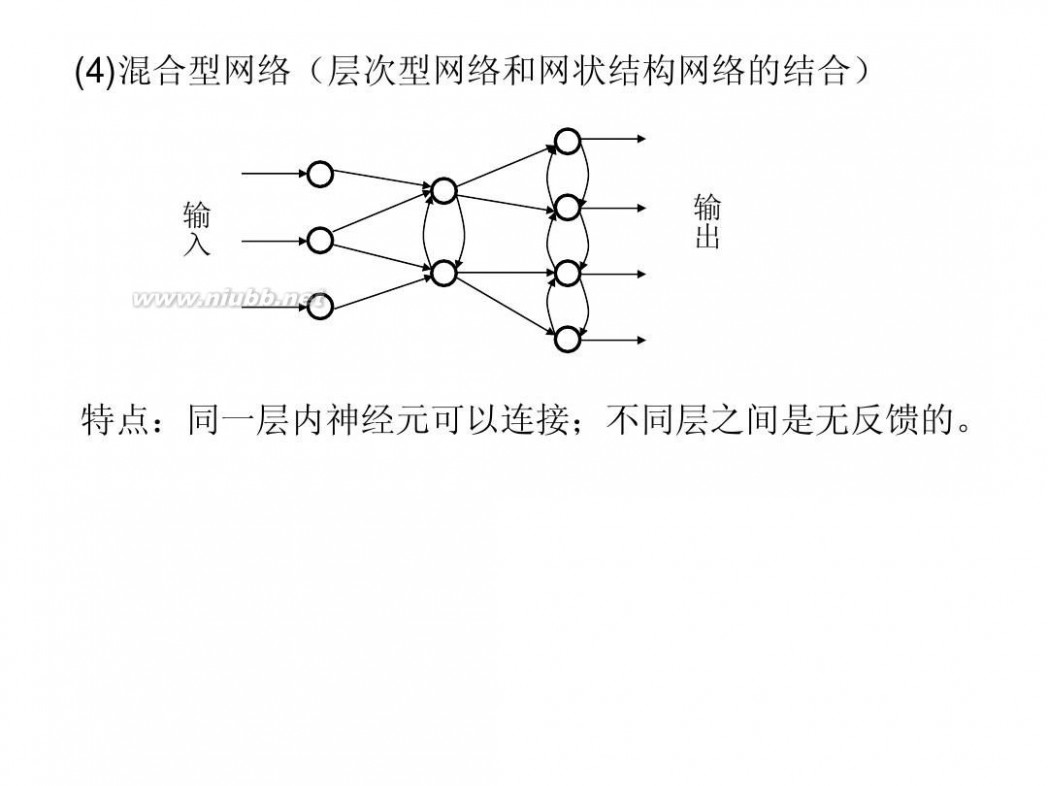
(4)混合型网络（层次型网络和网状结构网络的结合）
输 入 出 输

层

层

的

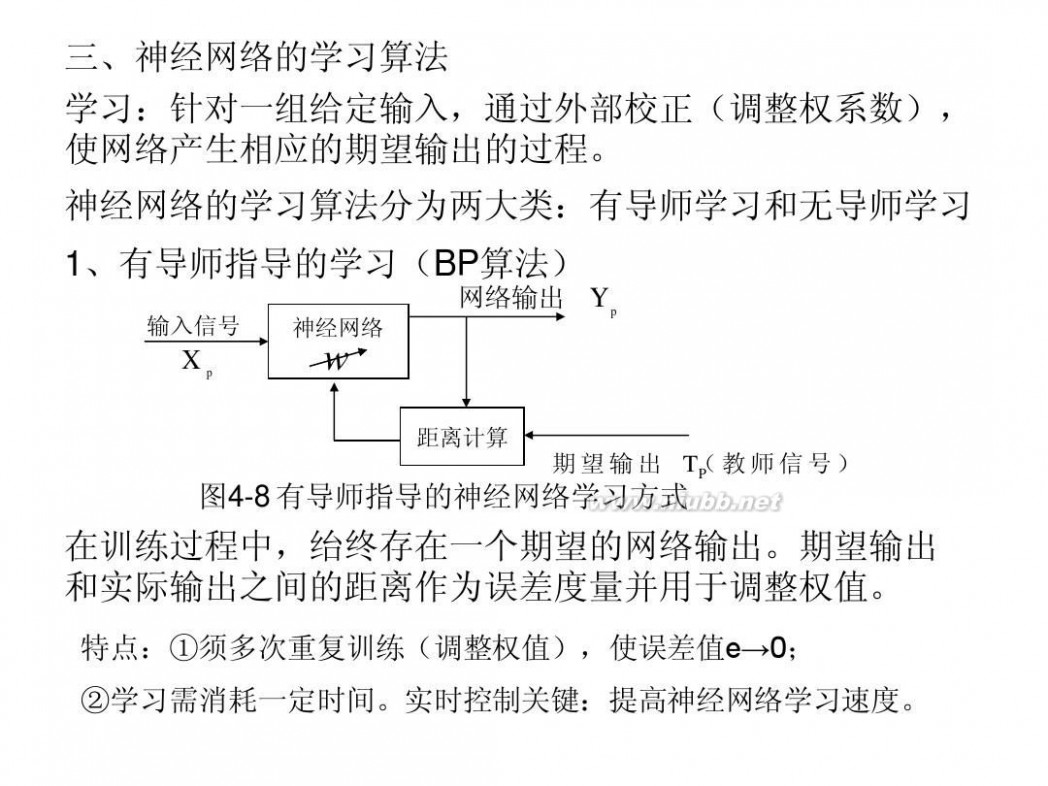
三、神经网络的学习算法 学习：针对一组给定输入，通过外部校正（调整权系数）， 使网络产生相应的期望输出的过程。 神经网络的学习算法分为两大类：有导师学习和无导师学习 1、有导师指导的学习（BP算法）
输入信号
神经网络

网络输出 Yp

Xp

w

期望输出　（教师信号） TP 图4-8 有导师指导的神经网络学习方式

距离计算

在训练过程中，绐终存在一个期望的网络输出。期望输出 和实际输出之间的距离作为误差度量并用于调整权值。
特点：①须多次重复训练（调整权值），使误差值e→0； ②学习需消耗一定时间。实时控制关键：提高神经网络学习速度。

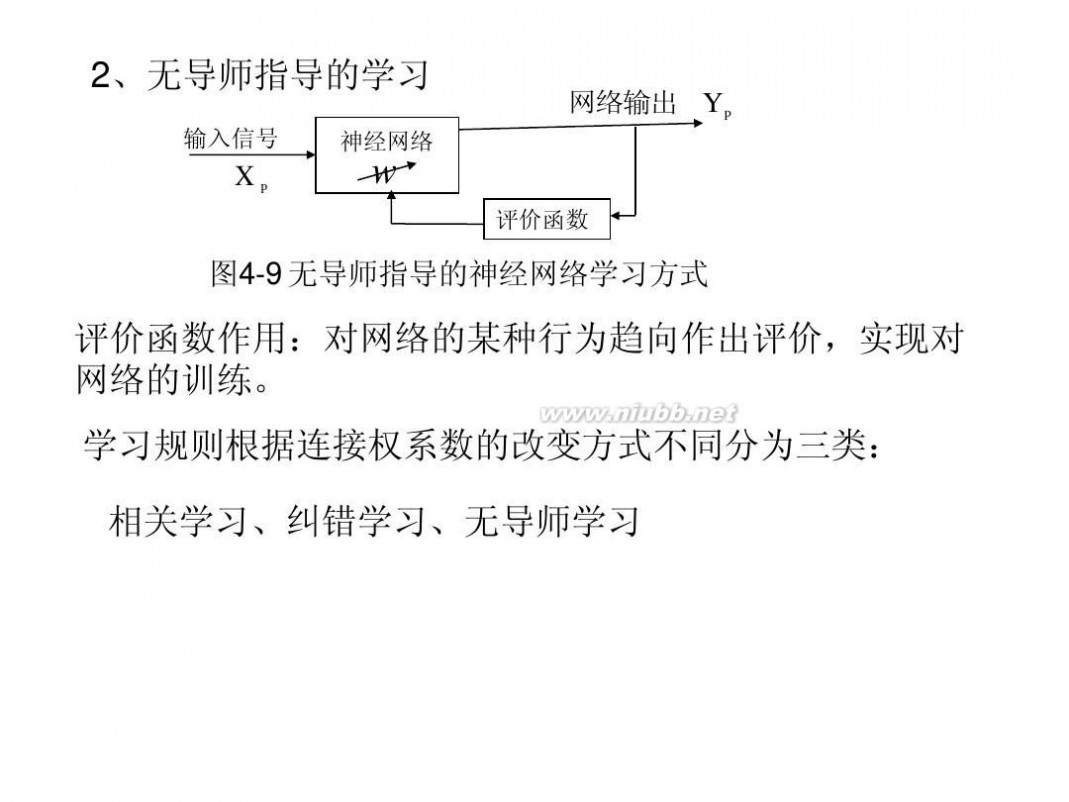
2、无导师指导的学习
输入信号

网络输出 YP

XP

神经网络 w

w

评价函数

图4-9 无导师指导的神经网络学习方式

评价函数作用：对网络的某种行为趋向作出评价，实现对 网络的训练。 学习规则根据连接权系数的改变方式不同分为三类： 相关学习、纠错学习、无导师学习

（1）相关学习（联想式） 特点：仅仅根据连接间的激活水平改变权系数。 它常用于自联想网络，执行特殊记忆状态的死记式学习。 学习算法：Hebb规则。 理论依据：突触前与突触后两者同时兴奋，即两个神经元 同时处于激发状态时，它们之间的连接强度将得到加强。

即 wij ( k + 1) = wij ( k ) + I i I j
下一时刻的权值 当前权值
n

激活水平

当 Neti = ∑ wij x j ? θ i
j =1

yi = f ( Neti )

时

则 wij ( k + 1) = wij ( k ) + y i y j

（2）纠错学习
特点：依赖关

于输出节点的外部反馈改变权系数。 它常用于感知器网络、多层前向传播网络。 学习方法：梯度下降法； 学习算法：δ规则(BP算法采用) 。

（3）无导师学习（竞争式学习）
特点：自动实现输入空间的检测和分类，调整权值以反映所观察事件 的分布。 它常用于ART网络。 步骤：1.识别与输入最匹配的节点。定义距离dj为接近距离测度，即
N ?1 i =0

d j = ∑ (ui ? wij ) 2

其中：ui(i=0,1, , N ? 1)为N 维输入向量（给定） L

具有最短距离的节点选作胜者。 2. 胜者的权向量经修正使该节点对输入u更敏感。 定义Nc，其半径逐渐减小至接近于0。 权值学习规则为： ?α (ui ? wij ), i ∈ N c ?wij = ? , i ? Nc ?0

其中：α 为步长（学习因子） 取值：0<α ≤ 1

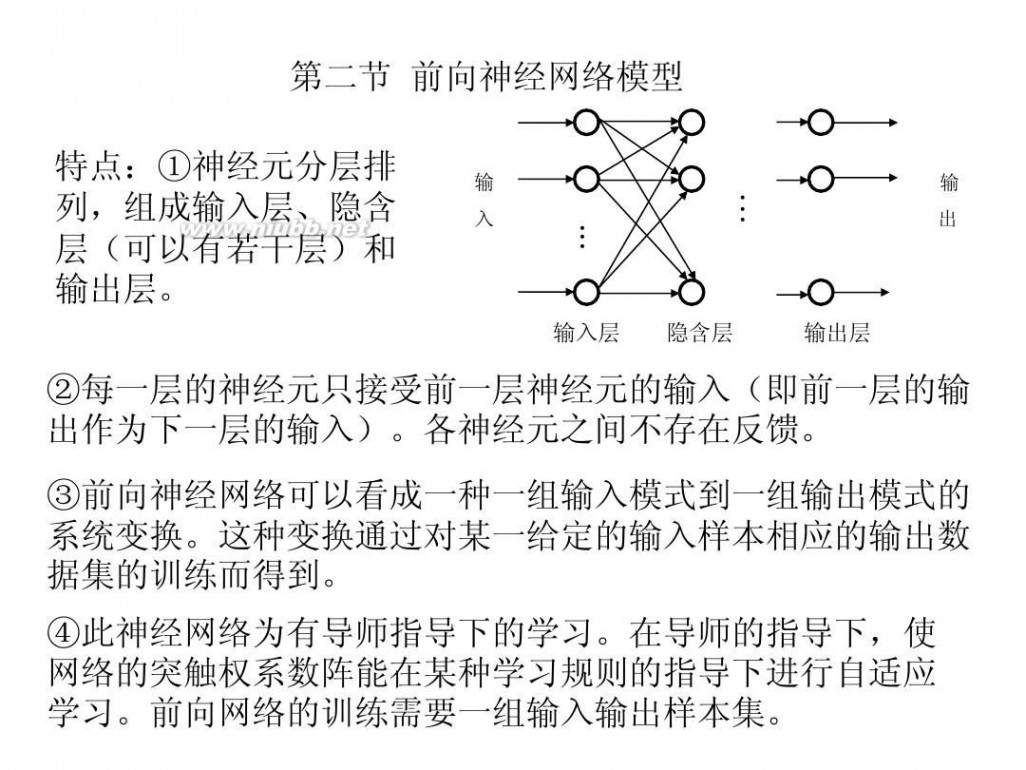
第二节 前向神经网络模型 特点：①神经元分层排 列，组成输入层、隐含 层（可以有若干层）和 输出层。
输 入
输 出

M
输入层 隐含层

M
输出层

②每一层的神经元只接受前一层神经元的输入（即前一层的输 出作为下一层的输入）。各神经元之间不存在反馈。 ③前向神经网络可以看成一种一组输入模式到一组输出模式的 系统变换。这种变换通过对某一给定的输入样本相应的输出数 据集的训练而得到。 ④此神经网络为有导师指导下的学习。在导师的指导下，使 网络的突触权系数阵能在某种学习规则的指导下进行自适应 学习。前向网络的训练需要一组输入输出样本集。

一、单一人工神经元

1
x1

θ0 w1
w2

x2

∑
n

Net　

f (?)

y

xn

Mw

图 单一人工神经元的示意图

Net = ∑ w j x j + θ 0
j =1

n

y = f ( Net )

式中：θ 0 为阈值 ； w j 是第j个输入的突触权系数(即权值)

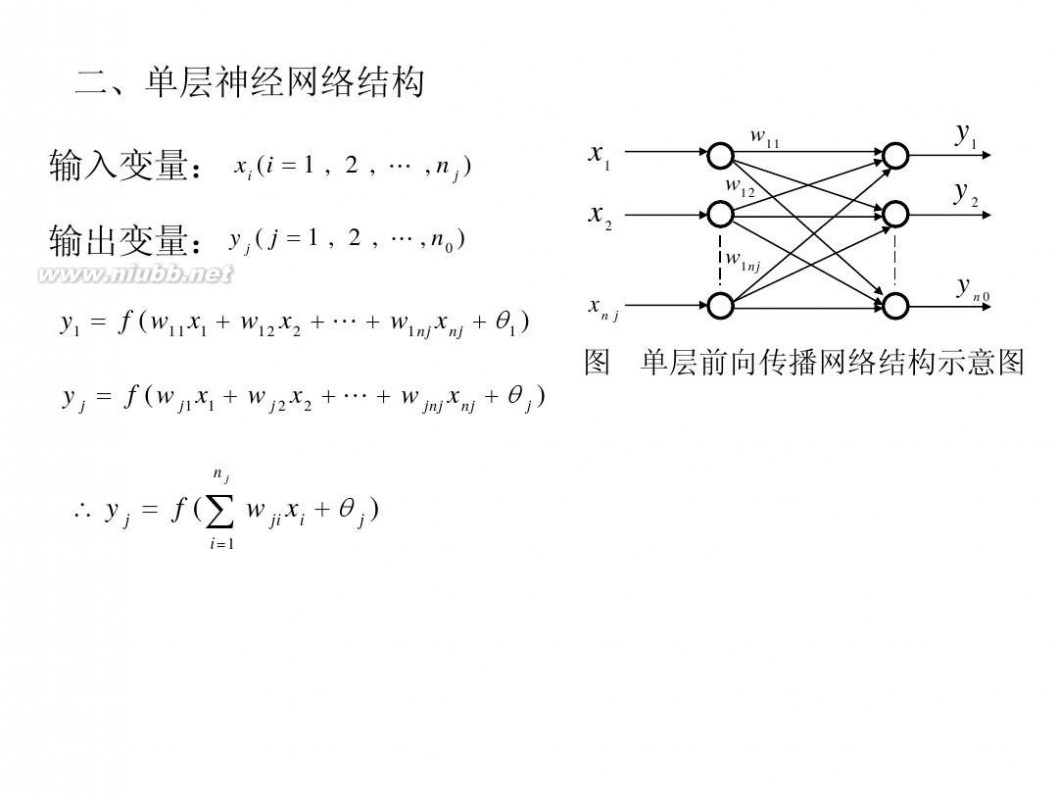
二、单层神经网络结构 输入变量： xi (i = 1 , 2 , L , n j ) 输出变量： y j ( j = 1 , 2 , L , n0 )
y1 = f ( w11 x1 + w12 x2 + L + w1nj xnj + θ1 ) y j = f ( w j1 x1 + w j 2 x2 + L + w jnj xnj + θ j )

x1
x2
xn j

w11
w12

y1
y2
yn 0

w1nj

图 单层前向传播网络结构示意图

∴ y j = f (∑ w ji xi + θ j )
i =1

nj

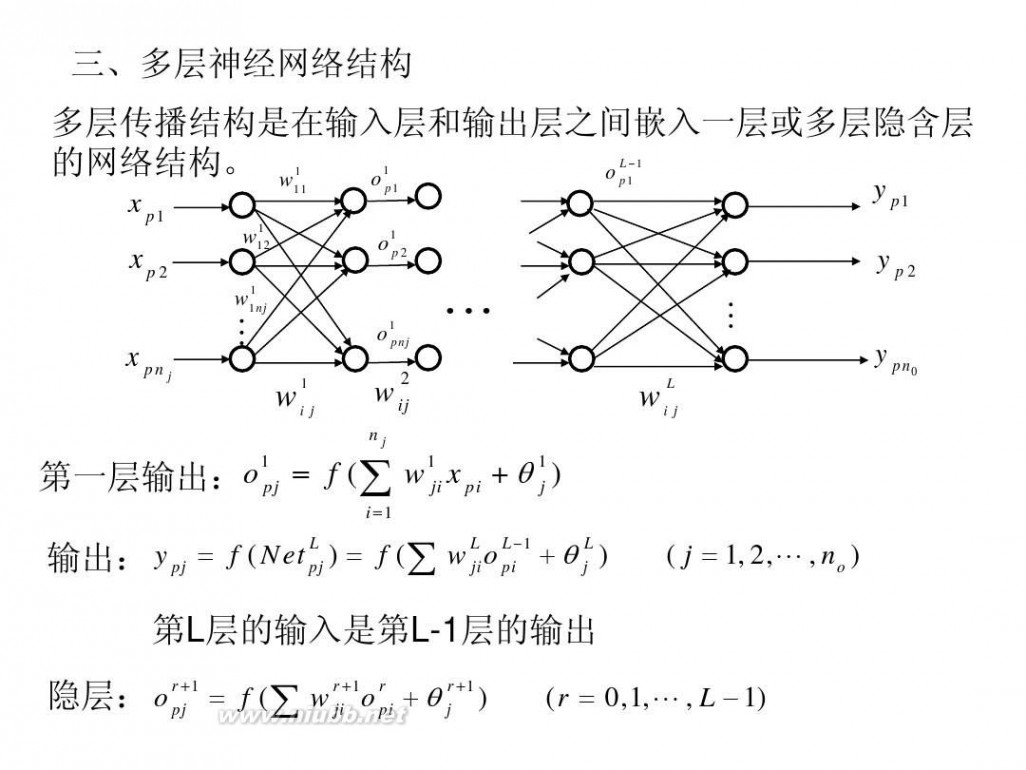
三、多层神经网络结构 多层传播结构是在输入层和输出层之间嵌入一层或多层隐含层 ? 的网络结构。 w1 o L1 1 p o1 1 p 11 y p1 x p1

xp2

1 w12

o1 2 p o1 pnj

1 w1nj

x pn j

M

L
wiLj

yp2

M
y pn0

wi j

1

2 wij
nj

o1 = f (∑ w1ji x pi + θ 1 ) 第一层输出： pj j
i =1
L L L ?1 L 输出： y pj = f ( Net pj ) = f (∑ w ji o pi + θ j )

( j = 1, 2,L , no )

第L层的输入是第L-1层的输出 隐层： o r +1 = f (∑ wrji+1o r + θ jr +1 ) pj pi
(r = 0,1,L , L ? 1)

四、多层传播网络的学习算法 (BP算法：误差反向传播学习算法)

x p1 xp2

w
1 w12

1 11

o

1 p1

L? o p1 1

t p1 t p2

y p1 yp2
y pn0

o1 2 p o1 pnj

1 w1nj

x pn j

M

L
wiLj

M t pn

o

前向传播网络实质：一种从输

入空间到输出空间的映射。 对于给定的输入矢量X，其网络的响应可以由Y=T(X)给出。 其中T为与网络结构相关的非线性算子。
X = ( x p1 , x p 2 ,L , x pnj ) Y = ( y p1 , y p 2 ,L , y pno )

wi1j

wi2 j

神经网络可以通过合适样本集，即输入输出矢量对(Xp,Tp)， (p=1,2, ···,N；p为样本数)，来进行训练。网络的训练实质上 是对突触权阵的调整，以满足当输入为Xp时其输出应为Tp。

x p1 xp2

w
1 w12
1 w1nj

1 11

o

1 p1

? o L1 1 p

t p1 t p2

y p1 yp2
y pn0

o1 2 p o1 pnj

x pn j

M

L
wi j
L

M t pn

o

wi j

1

wi2 j

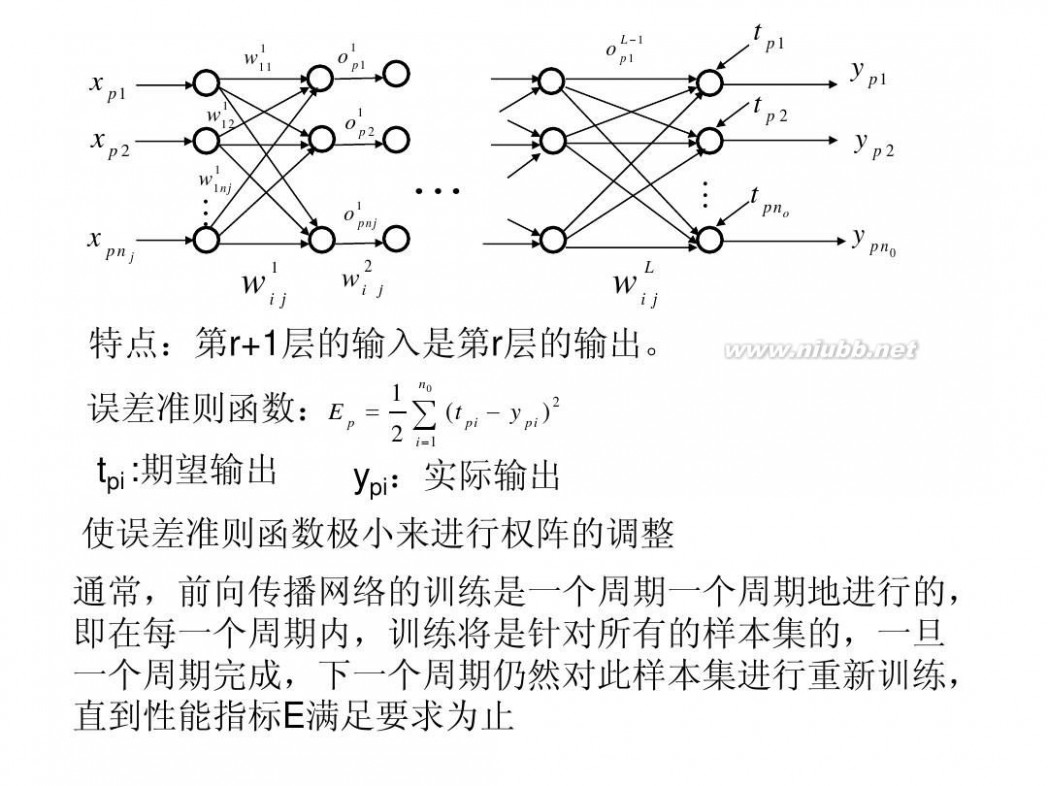
特点：第r+1层的输入是第r层的输出。
1 n0 误差准则函数：E p = ∑ (t pi ? y pi ) 2 2 i =1

tpi :期望输出

ypi：实际输出

使误差准则函数极小来进行权阵的调整 通常，前向传播网络的训练是一个周期一个周期地进行的， 即在每一个周期内，训练将是针对所有的样本集的，一旦 一个周期完成，下一个周期仍然对此样本集进行重新训练， 直到性能指标E满足要求为止

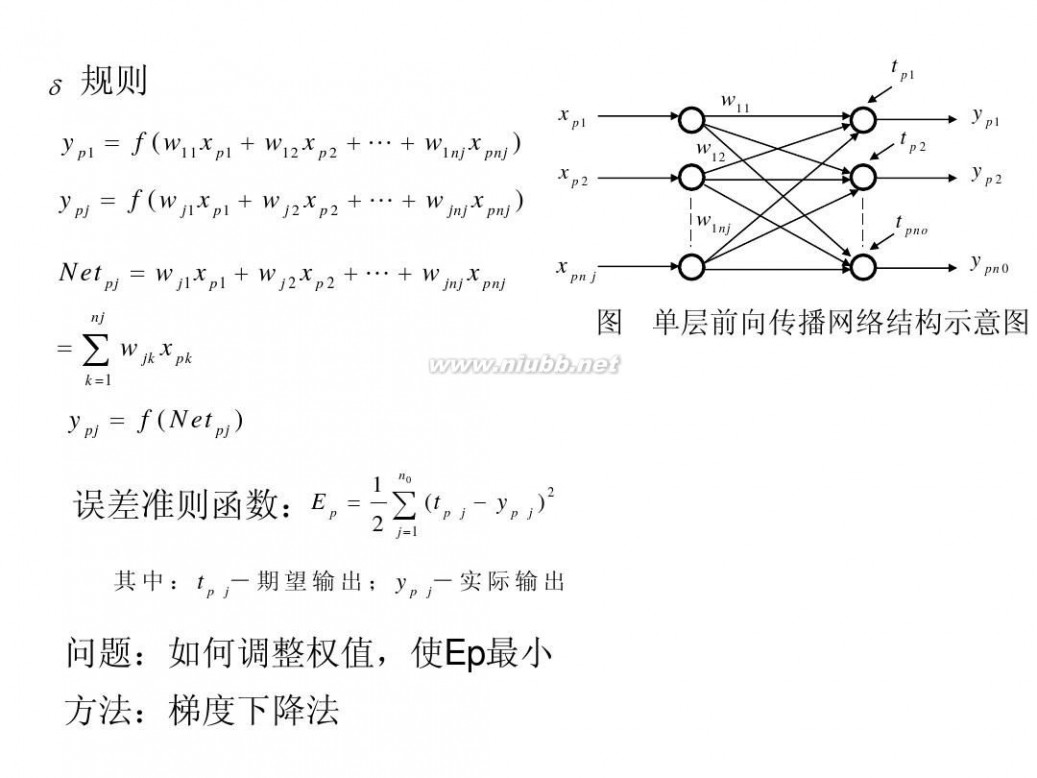
δ 规则

t p1

y p1 = f ( w11 x p1 + w12 x p 2 + L + w1nj x pnj ) y pj = f ( w j1 x p1 + w j 2 x p 2 + L + w jnj x pnj )
Net pj = w j1 x p1 + w j 2 x p 2 + L + w jnj x pnj = ∑ w jk x pk
k =1 nj

x p1
xp2

w11 w12 w1nj
t p2 t pno

y p1

y p2

x pn j

y pn 0

图 单层前向传播网络结构示意图

y pj = f ( Net pj )
1 n0 2 误差准则函数：E p = 2 ∑ (t p j ? y p j ) j =1

其中：t p j－期望输出；y p j－实际输出

问题：如何调整权值，使Ep最小 方法：梯度下降法

梯度下降法公式：
?E p ?w ji Q ?E p ?Net pj = ?E p ?Net pj ?E p ?y pj
nj

? ?E p ?w ji = η ? ? ? ?w ji ?

? ? ? ?

η为学习步长

?

?Net pj ?w ji ?y pj
=

复合求导规则
1 ? 2(t pj ? y pj )(?1) ? f ′( Net pj ) 2

=

?

?Net pj

?Net pj ?w ji

=

? ∑ x pk w jk
k =1

?w ji
?E p

= x pi

δ 定义：pj = ? ?Net = (t pj ? y pj ) f ′( Net pj ) （广义误差）
pj

则：?w ji = η (?1) ? (t pj ? y pj )(?1) f ′( Net pj ) ? x pi = η ? δ pj ? x pi

?w ji = η ? δ pj ? x pi

δ pj = ?
1 p1

?E p ?Net pj

= (t pj ? y pj ) f ′( Net pj )
L? o p1 1

x p1 xp2

w
1 w12
1 w1nj

1 11

o

t p1 t p2

y p1 yp2
y pn0
?E p ?Net r pj

o1 2 p o1 pnj

x pn j

M

L
wiLj

M t pn
r pj

o

wi1j

wi2 j

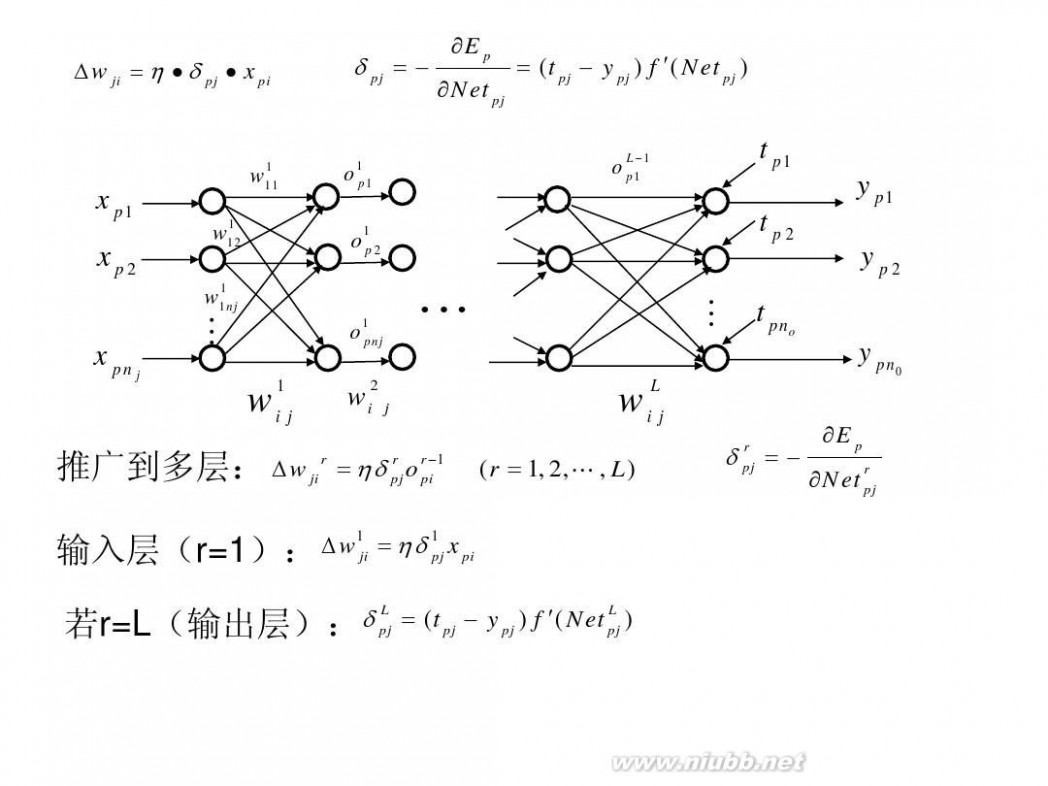
r 推广到多层： ?w ji r = ηδ pj o rpi?1 (r = 1, 2,L , L)

δ =?

?w1ji = ηδ 1 x pi pj 输入层（r=1）：
L L δ pj = (t pj ? y pj ) f ′( Net pj ) 若r=L（输出层）：

1 取： f ( Net pj )＝ Sigmoid型(S型)激励函数 -Netpj 1＋e -Net 1 0-1 ? e pj (?1) f ′( Net pj )＝( )′ = -Netpj -Netpj 2 (1＋e ) 1＋e 1 e pj = ? -Netpj -Netpj (1＋e ) (1＋e )
＝f ( Net pj )[1 ? f ( Net pj )] ∴ f ′( Net pj )＝f ( Net pj )[1 ? f ( Net pj )]
-Net

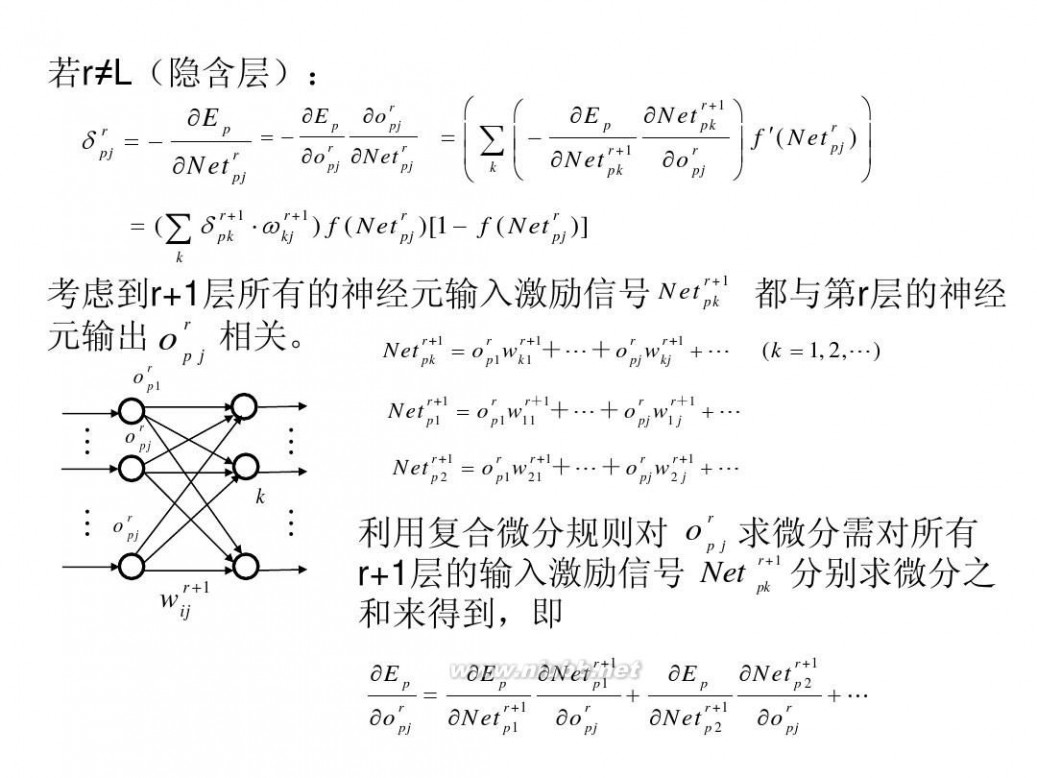
若r≠L（隐含层）：
r δ pj = ?

?E p ?Net
k

r pj

=

?

?E p ?o r pj
r ?o r ?Net pj pj

? ? ? ?E p ?Net r +1 ? pk r = ?∑? ? f ′( Net pj 　 )? ? ?Net r +1 ?o r ? ? ? k ? pk pj ? ? ? ?

r+ r r = (∑ δ pk 1 ? ωkj+1 ) f ( Net r )[1 ? f ( Net pj )] pj

考虑到r+1层所有的神经元输入激励信号 Net pk 都与第r层的神经 r + r 元输出 o p j 相关。 Net r +1 = o r 1wkr1 1＋L＋o r wkj+1 + L (k = 1, 2,L) pk p pj
or 1 p

r +1

M M

or pj
k

M M

r＋ Net r +1 = o r 1w11 1＋L＋o r w1r＋1 + L p1 p pj j r+ r Net r +1 = o r 1w21 1＋L＋o r w2 +1 + L p2 p pj j

o

r pj

r wij +1

r o p j 求微分需对所有 利用复合微分规则对 r Net pk+1 分别求微分之 r+1层的输入激励信号

和来得到，即
?E p ?o
r pj

=

?E p ?Net
r +1 p1

r+ ?Net p11

?o

r pj

+

?E p ?Net
r +1 p2

r ?Net p+1 2

?o

r pj

+L

计算步骤：

初始化

wij 、θj、最大容许误差E、η

给定输入向量Xp和期望目标输出Tp

计算各层输出 前向计算 求误差Ep
L r 求广义误差δ pj，δ pj

误差反向计算 网络权阵的更新是通过反 向传播网络的期望输出 （样本输出）与实际输出 的误差来实现的。

调整权值 N Ep≤E Y 结束

注意的有关问题： （1）权系数的初值 权系数通常初始化成小的随机值，尽量 可能覆盖整个权阵的空间域。 （2）学习方式 ①单样本学习：每输入一个样本就进行一次学习，然后提 供下一个样本重复学习（适合在线学习）。 ②批量学习：样本集全部输入到神经网络中，才进行一 次权值调整（适合离线学习）。
1 p E= ∑ 2 p =1 (t pi ? y pi ) 2 ∑
i =1 n0

（3）激励函数 采用S型激励函数时，由于输出层各神经元 的输出只能趋于1或0，不能达到1或0。在设置各训练样本时， 期望的输出分量不能设置为1或0，以设置0.95或0.05较为适 宜。

（4）学习速度η 学习速率越大，收剑越快，但容易产生振荡； 而学习速率越小，收剑越慢。 η一般取值0.001～0.1。 学习开始阶段， η选较大的值可以加快学习速度；学习接近优 化区时， η值必须相当小，否则权值将产生振荡而不收敛。 （5）局部极小问题 BP学习不可避免地存在局部极小问题， 且学习速度很慢，甚至会在极值点附近出现振荡现象，而不 能平滑地趋于最优解。 解决方案：加动量项(momentum)
r 即?w ji r (k ) = ηδ pj o r ?1 + α?w ji r (k ? 1) pi

r r r 其中： ?w ji (k ) = w ji (k )－w ji (k ? 1) r ηδ pj o r ?1：标准BP项 pi

?w ji r (k－1) = w ji r (k－1)－w ji r (k ? 2)

动量项：α?w ji r (k ? 1)

α：动量因子（常数，取值0～1间）

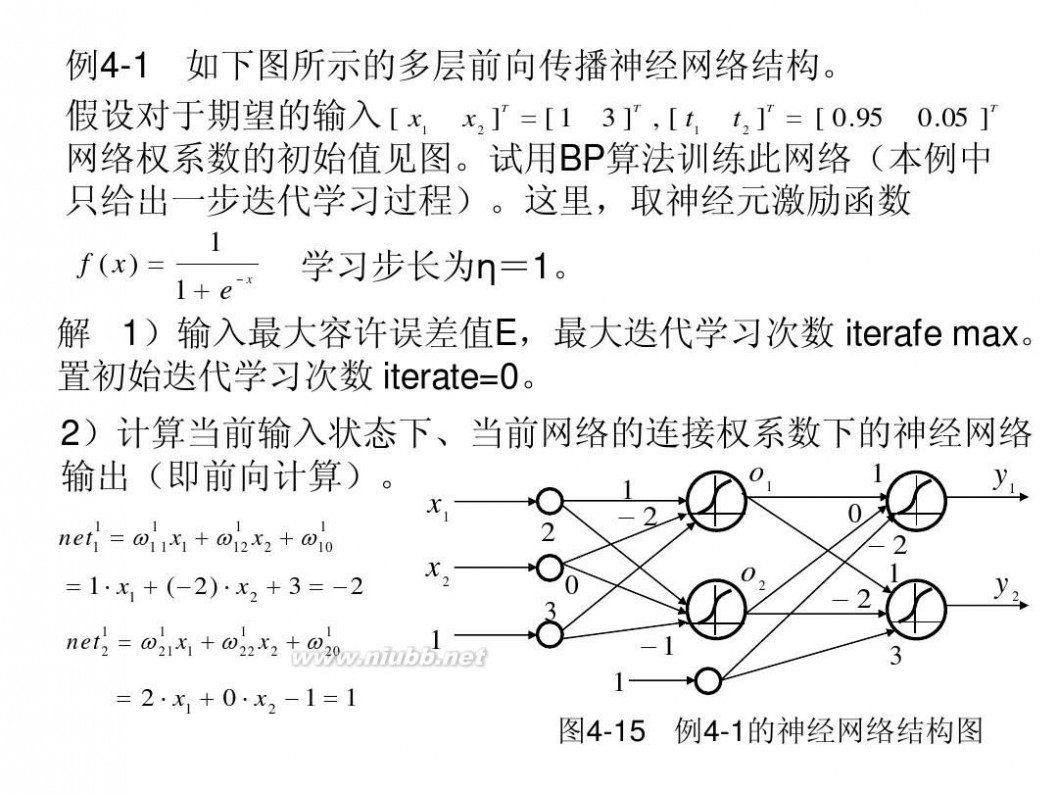
例4-1 如下图所示的多层前向传播神经网络结构。 　 假设对于期望的输入 [ x x ] = [ 1 3 ] , [ t t ] = [ 0.95 0.05 ] 网络权系数的初始值见图。试用BP算法训练此网络（本例中

只给出一步迭代学习过程）。这里，取神经元激励函数 1 f ( x) = 学习步长为η＝1。 1 + e?x 解 1）输入最大容许误差值E，最大迭代学习次数 iterafe max。 置初始迭代学习次数 iterate=0。
T T T T 1 2 1 2

1 1 1 1 net1 = ω1 1 x1 + ω12 x2 + ω10

2）计算当前输入状态下、当前网络的连接权系数下的神经网络 o1 1 y1 输出（即前向计算）。 1 x1 0 ?2
2
= 1 ? x1 + (?2) ? x2 + 3 = ?2
net = ω x + ω x + ω
1 2 1 21 1 1 22 2 1 20

x2
1
3

0

o2
?1

?2 1 ?2
3

y2

= 2 ? x1 + 0 ? x2 ? 1 = 1

1

图4-15 例4-1的神经网络结构图

o = f (net ) =
1 1 1 1

1 1+ e
1+ e
1 ? net1

1 = = 0.1192 2 1+ e
1 = = 0.731 ?1 1+ e

o = f (net ) =
1 2 1 2

1
? net1 2

1 2 1 2 2 net12 = ω11o1 + ω12o1 + ω10 = 1 ? o1 + 0 ? o1 ? 2 = ?1.8808 2 2
1 2 2 1 2 2 net2 = ω21o1 + ω22 o1 + ω20 = 1? o1 + (?2) ? o1＋3 = 1.6572 2 2

y1 = f (net12 ) =

1 1+ e
2 ? net1

= 0.1323

2 y2 = f (net2 ) =

1 1+ e
2 ? net2

= 0.8399

3)判断神经网络最大容许误差满足要求或迭代学习达到最大 容许值否？ 1 1 2 2 2 2
Ep =

∑ (t 2
i =1

pi

? y pi ) = [(t1 ? y1 ) + (t2 ? y2 ) ] 2

E p p E or iterate ≥ iteratemax

若上述不等式中有一个满足，则退出学习。否则进入4）。

4）计算广义误差。 输出层广义误差：
δ12 = (t1 ? y1 ) f ′(net12 ) = (t1 ? y1 ) f (net12 )[1 ? f (net12 )]
= (t1 ? y1 ) y1 (1 ? y1 ) = 0.0938
2 δ 22 = (t2 ? y2 ) f ′(net2 ) = (t2 ? y2 ) y2 (1 ? y2 ) = 0.1062

误 差 反 向 传 播

隐含层广义误差：
1 1 1 1 δ11 = ∑ δ k2ωk21 f ( Net1 )[1 ? f ( Net1 )] = ∑ δ k2ωk21o1 (1 ? o1 ) K =1 K =1
2 2 1 1 = (δ12ω11 + δ 22ω21 )o1 (1 ? o1 ) = 0.2811

2

2

2 2 1 1 1 1 1 δ 2 = ∑ δ k2ωk22 f ( Net2 )[1 ? f ( Net2 )] = ∑ δ k ωk 2o2 (1 ? o2 )

2

2

K =1

K =1

2 2 = (δ12ω12 + δ 22ω22 )o1 (1 ? o1 ) = ?0.04176 2 2

5）连接权系数更新
?w ji = ηδ o
r r r ?1 j i

(r = 1, 2)

?w1ji = ηδ 1 xi j
1 1 ?ω21 = ηδ 2 x1 = ?0.04176

1 例如： ?ω11 = ηδ11 x1 = 0.2811

1 ?ω10 = ηδ11 ? 1 = 0.2811

?ω = ηδ o = 0.0112
2 11 2 1 1 1

2 ?ω20 = ηδ 22 ? 1 = 0.1062

ω lji (iterate + 1) = ω lji (iterate) + ?ω lji l = 1 , 2 ; i = 0 , 1 , 2 ; j = 1 , 2
iterate ＝ iterate + 1 ；

继续迭代计算直至满足终止条件为止

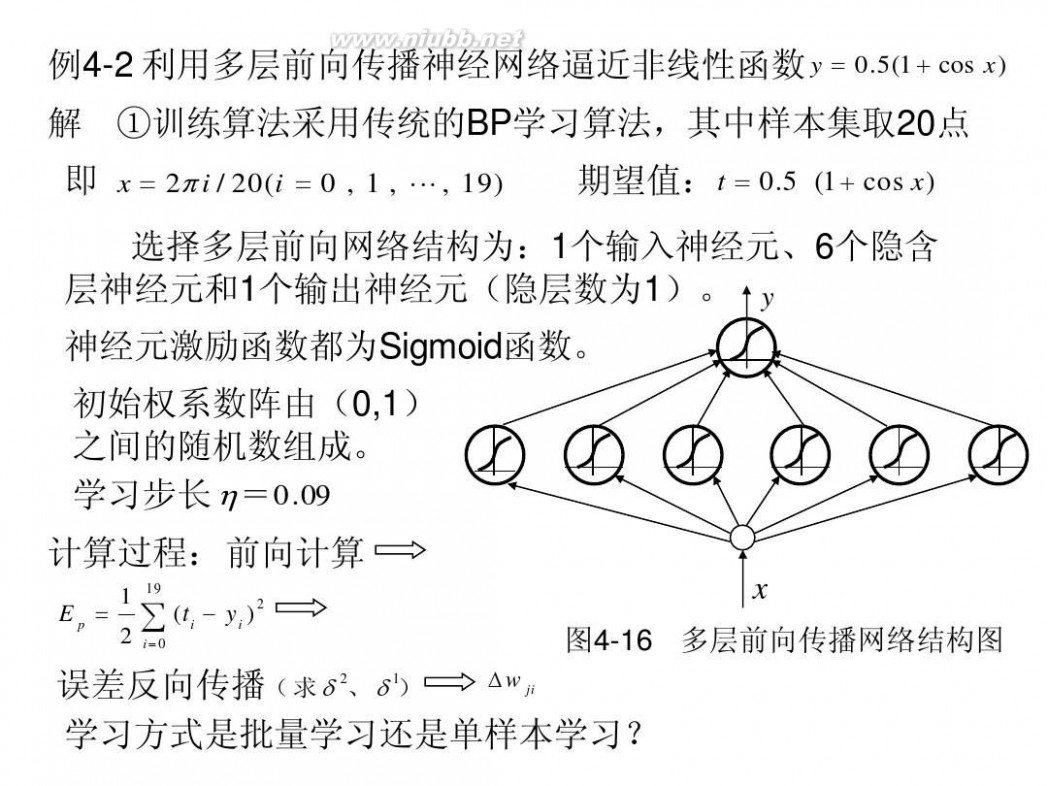
例4-2 利用多层前向传播神经网络逼近非线性函数 y = 0.5(1 + cos x) 解 ①训练算法采用传统的BP学习算法，其中样本集取20点 即 x = 2π i / 20(i = 0 , 1 , L , 19) 期望值： t = 0.5 (1 + cos x)

选择多层前向网络结构为：1个输入神经元、6个隐含 层神经元和1个输出神经元（隐层数为1）。 y 神经元激励函数都为Sigmoid函数。 初始权系数阵由（0,1） 之间的随机数组成。 学习步长 η＝0.09 计算过程： 前向计算
1 19 E p = ∑ (ti ? yi ) 2 2 i =0

x
图4-16 多层前向传播网络

结构图

?w ji 误差反向传播（求δ 2、δ 1） 学习方式是批量学习还是单样本学习？

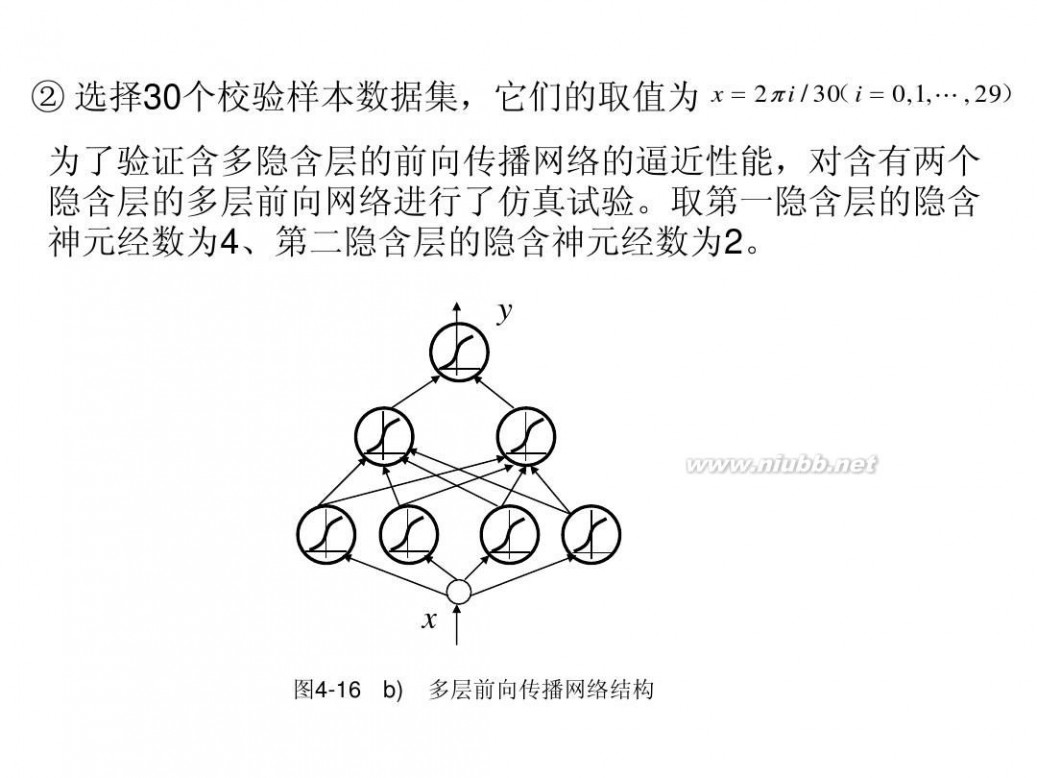
（ ② 选择30个校验样本数据集，它们的取值为 x = 2π i / 30 i = 0,1,L , 29）

为了验证含多隐含层的前向传播网络的逼近性能，对含有两个 隐含层的多层前向网络进行了仿真试验。取第一隐含层的隐含 神元经数为4、第二隐含层的隐含神元经数为2。

y

x
图4-16 b) 多层前向传播网络结构

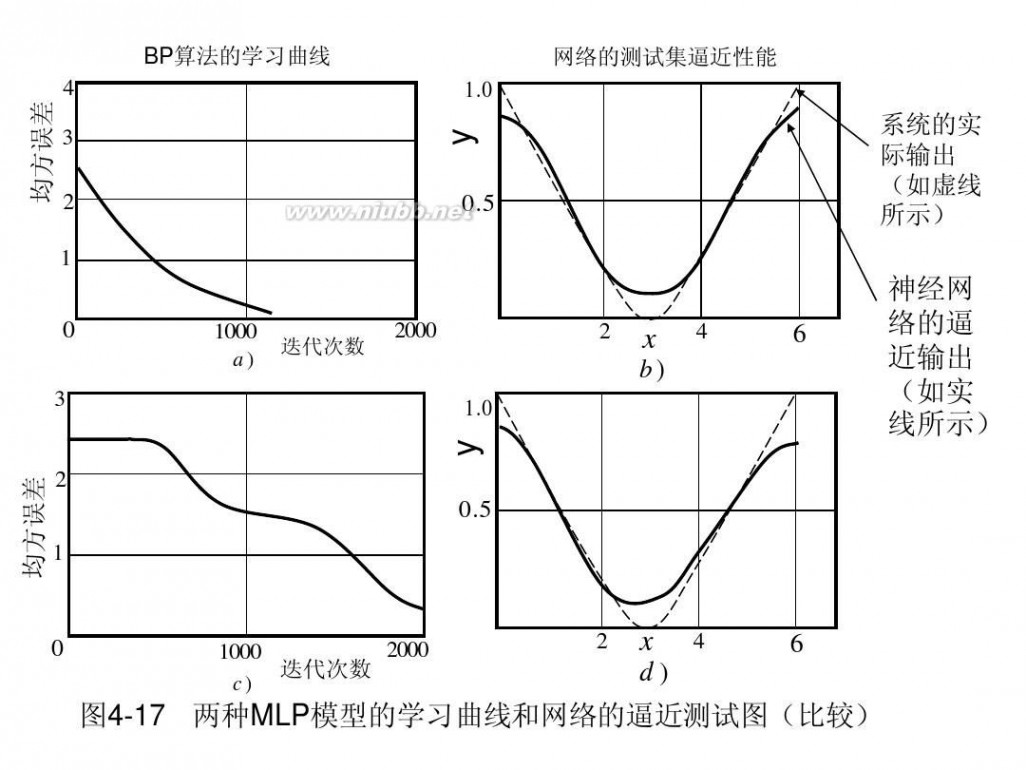
BP算法的学习曲线

网络的测试集逼近性能

均方误差

4

1.0
系统的实 际输出 （如虚线 所示）

3
2
1

y
0.5

0
3
均方误差

2000 1000 迭代次数 a)

2

b)
1.0

x

4

6

神经网 络的逼 近输出 （如实 线所示）

2

1

y
0.5

0

2000 1000 迭代次数 c)

2

d)

x

4

6

图4-17 两种MLP模型的学习曲线和网络的逼近测试图（比较）

结论：增加隐含层的数目并不一定意味着能够改善逼近精度 （隐含层越多，计算量越大，收敛速度就受影响——慢）。 对于本例而言，这一非线性函数的神经网络逼近问题用单一 隐含层已经足以满足逼近精度了。

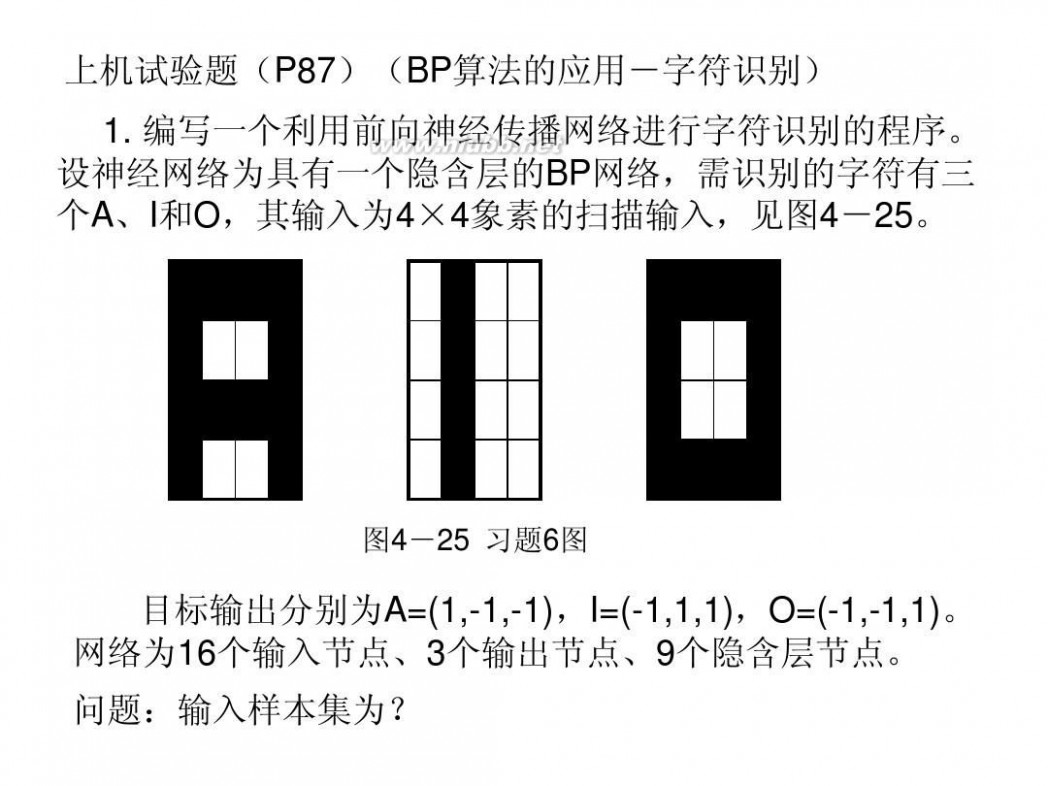
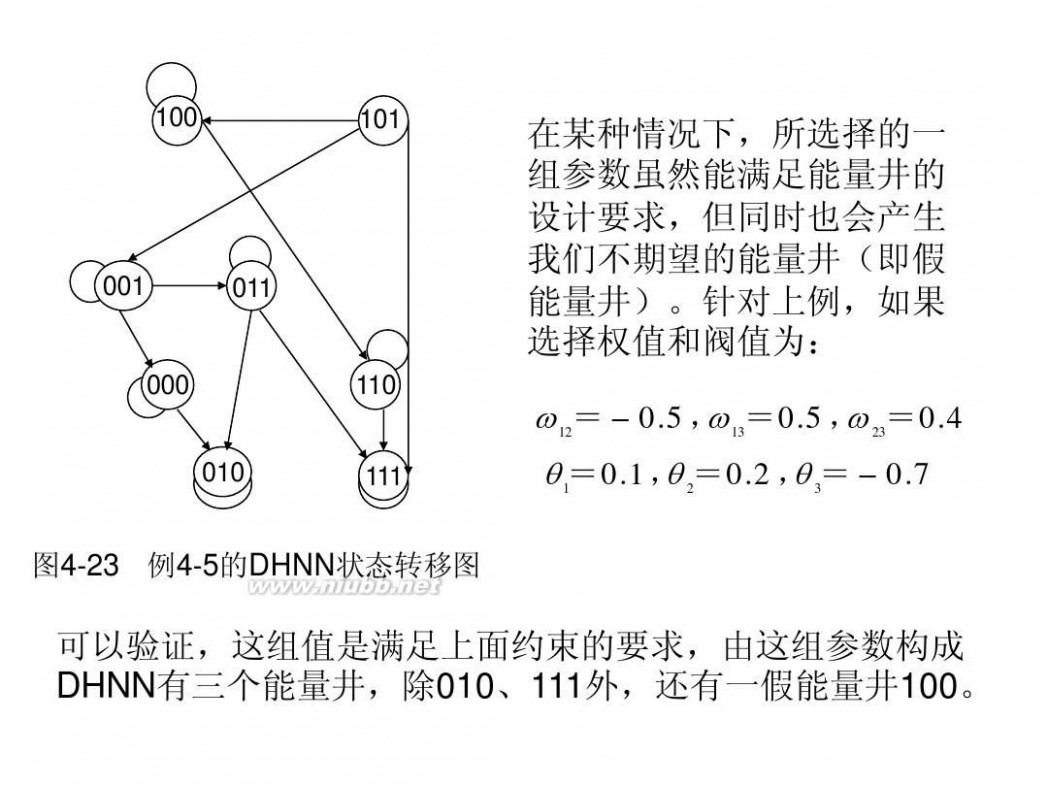
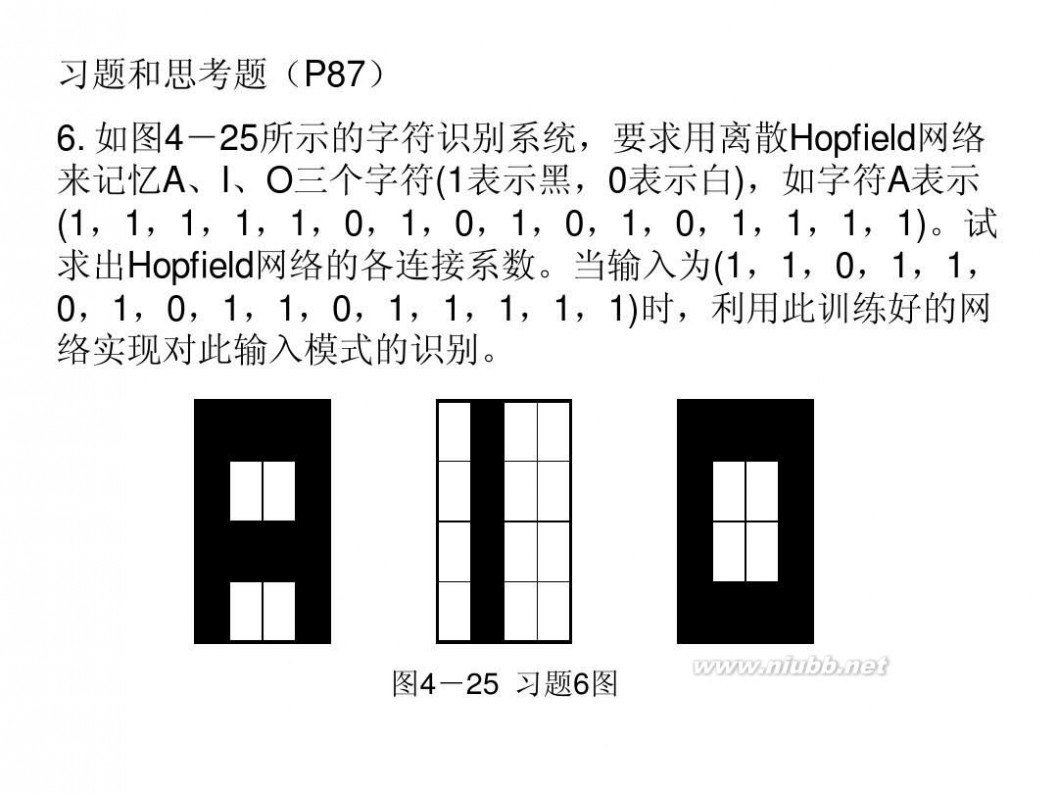
上机试验题（P87）（BP算法的应用－字符识别） 1. 编写一个利用前向神经传播网络进行字符识别的程序。 设神经网络为具有一个隐含层的BP网络，需识别的字符有三 个A、I和O，其输入为4×4象素的扫描输入，见图4－25。

图4－25 习题6图

目标输出分别为A=(1,-1,-1)，I=(-1,1,1)，O=(-1,-1,1)。 网络为16个输入节点、3个输出节点、9个隐含层节点。 问题：输入样本集为？

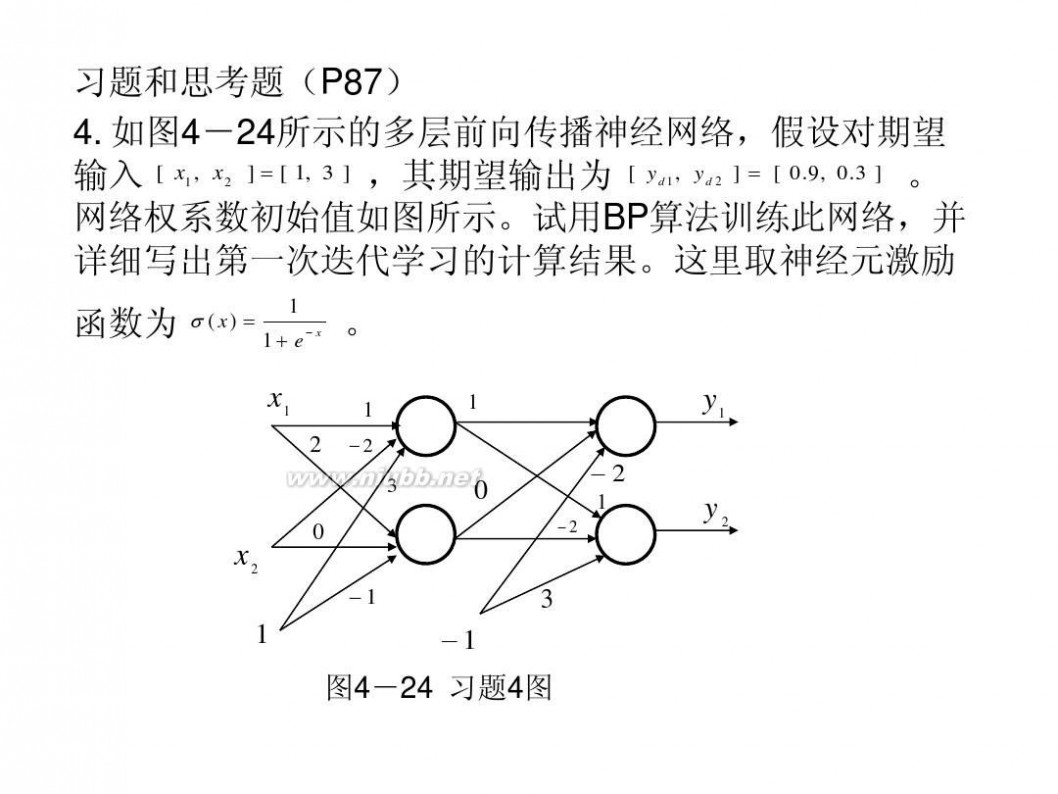
习题和思考题（P87） 4. 如图4－24所示的多层前向传播神经网络，假设对期望 　 输入 [ x1 , x2 ] = [ 1, 3 ] ，其期望输出为 [ yd 1 , yd 2 ] = [ 0.9, 0.3 ] 。 网络权系数初始值如图所示。试用BP算法训练此网络，并 详细写出第一次迭代学习的计算结果。这里取神经元激励 函数为 σ ( x) = 1 + e? x 。
1

x1
2

1 ?2

1

y1
?2
?2

3

0

1

x2
1

0
?1

y2

3

?1
图4－24 习题4图

第三节 动态神经网络模型 前向传播网络特点： ①从学习观点看是一种强有力的学习系统，系统结构简单 且易于编程； ②从系统观点看是一种静态非线性映射，通过简单非线性 处理单元的复合映射可获得复杂的非线性处理能力； ③从计算观点看不是一种强有力的系统，缺乏丰富的动力 学行为，大部分前向神经网络都是学习网络，并不注重系 统的动力学行为。 反馈型神经网络：非线性动力学系统。具备丰富的动力学 特征，如稳定性、极限环、奇异吸引子（即浑沌现象）等 。

反馈动力学神经网络系统的两个重要特征： 1）系统有若干个稳定状态（称为记忆）。如果从某一初始 状态开绐运动，系统总可以进入某一稳定状态（即寻找记忆 的过程）。稳态的存在是

实现联想记忆的基础。 2）系统的稳定状态可以通过改变相连单元的权值而产生。 难点：怎样通过调整网络权值来产生需要的稳定状态。 稳定性定义： 定义4-1 神经网络从任一初态X(0)开绐运动，若存在某一 有限的时刻ts。从ts以后神经网络的状态不再发生变化，即 X (t + ?t ) = X (t ) , ?t > 0 ，则称网络是稳定的。处于稳定时 刻的网络状态叫稳定状态，又称定点吸引子。
s s

定点吸引子：相空间（即状态空间）的一个不动点。 吸引子分类：稳定的吸引子（如定点吸引子）；不稳定的 吸引子（如极限环吸引子－周期重复的循环）。

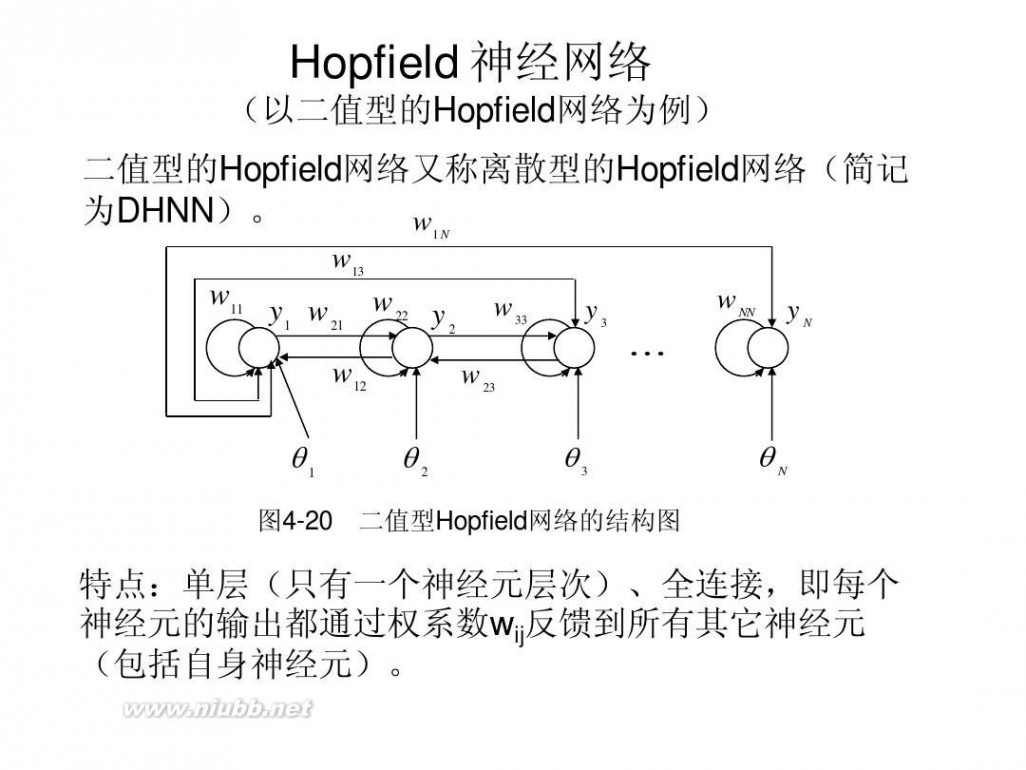
Hopfield 神经网络
（以二值型的Hopfield网络为例） 二值型的Hopfield网络又称离散型的Hopfield网络（简记 为DHNN）。 w1 N w13 w11 y w w22 wNN y y3 y2 w33 N 1 21

w12

w23

L

θ1

θ2

θ3

θN

图4-20 二值型Hopfield网络的结构图

特点：单层（只有一个神经元层次）、全连接，即每个 神经元的输出都通过权系数wij反馈到所有其它神经元 （包括自身神经元）。

节点方程式：
Neti ( k ) = ∑ ωi j y j (k ) + θi
j =1 N

?1, ? yi (k + 1) = f ( Neti (k )) = ? ?0, ?

Neti (k ) > 0 Neti (k ) ≤ 0

阈值型激 励函数

式中：K表示时间变量； θ i 表示外部输入(阀值)；yi 表示神 经元输出； Neti 表示神经元内部状态；f()表示阀值函数。 某一时刻的网络状态可以用一个包含0和1的矢量来表示， 如 Y = ( y1 y2 L yn ) 。 状态变化采用随机性异步更新策略。 随机性异步更新策略特点：每次只有一个神经元节点进行状态 的调整计算（即随机地选择下一个要更新的神经元，且允许所 有神经元节点具有相同的平均变化概率） ，其它节点状态均保 持不变。
yi (k + 1) = f (∑ wij y j (k ) + θi )
y j (k + 1) = y j (k ) ( j ≠ i)

节点状态更新包括三种情况：0→1、1→0，或状态保持。 某一时刻网络中只有一个节点被选择进行状态更新，当该节 点状态变化时，网络状态就可以以某一概率转移到另一状态； 当该节点状态保持时，网络状态更新的结果保持前一时刻状 态。 网络从某一初始状态开始经多次更换状态才能达到某一 稳定状态。给定网络的权值和阀值，就可以确定网络的状态 转移序列。

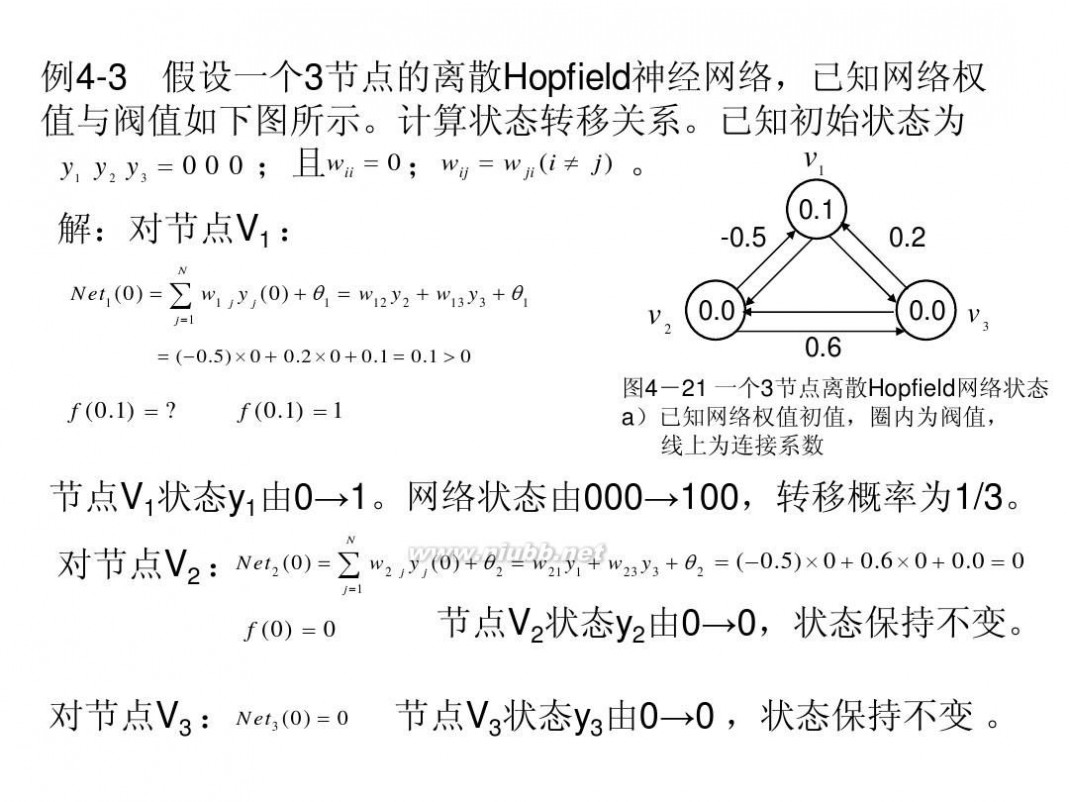
例4-3 假设一个3节点的离散Hopfield神经网络，已知网络权 值与阀值如下图所示。计算状态转移关系。已知初始状态为 v1 y y y = 0 0 0 ；且wii = 0 ；wij = w ji (i ≠ j ) 。
1 2 3

解：对节点V1 ：
Net1 (0) = ∑ w1 j y j (0) + θ1 = w12 y2 + w13 y3 + θ1
j =1 N

0.1 -0.5 0.2 0.0 0.6
图4－21 一个3节点离散Hopfield网络状态 4 21 3 Hopfield a）已知网络权值初值，圈内为阀值， 线上为连接系数

v2

0.0

v3

= (?0.5) × 0 + 　 × 0 + 0.1 = 0.1 > 0 0.2

f (0.1) =

?

f (0.1) = 1

节点V1状态y1由0→1。网络状态由000→100，转移概率为1/3。 对节点V2 ：Net2 (0) = ∑ w2 j y j (0) + θ 2 = w21 y1 + w23 y3 + θ 2 = (?0.5) × 0 + 0.6 × 0 + 0.0 = 0
j =1 N

f (0) = 0

节点V2状态y2由0→0，状态保持不变。 节点V3状态y3由0→0 ，状态保持不变 。

对节点V3 ： Net3 (0) = 0

1/3

110 0.4 1/3 1/3 001 0.0 2/3 2/3

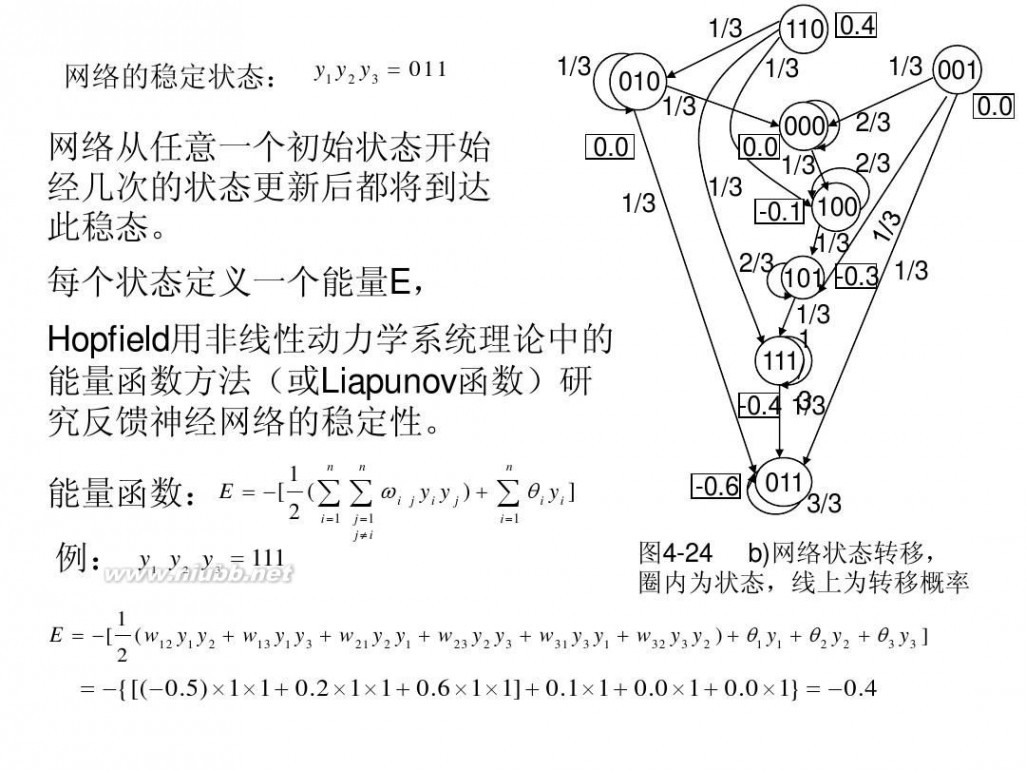
网络的稳定状态： y1 y2 y3 = 011

1/3

010 1/3 0.0 1/3

网络从任意一个初始状态开始 经几次的状态更新后都将到达 此稳态。 每个状态定义一个能量E，

0.0 1/3

000 1/3

Hopfield用非线性动力学系统理论中的 能量函数方法（或Liapunov函数）研 究反馈神经网络的稳定性。
n 1 n n 能量函数： E = ?[ 2 (∑∑ ωi j yi y j ) + ∑θi yi ] i =1 j =1 i =1

-0.1 100 1/3 2/3 101 -0.3 1/3 1/3 1 111/ 3 -0.4 1/3

-0.6 011

3/3

例： y y y = 111
1 2 3

j ≠i

图4-24 b)网络状态转移， 圈内为状态，线上为转移概率

1 E = ?[ ( w12 y1 y2 + w13 y1 y3 + w21 y2 y1 + w23 y2 y3 + w31 y3 y1 + w32 y3 y2 ) + θ1 y1 + θ 2 y2 + θ3 y3 ] 2

= ?{[(?0.5) ×1×1 + 0.2 ×1×1 + 0.6 ×1×1] + 0.1×1 + 0.0 ×1 + 0.0 ×1} = ?0.4

y1 y2 y3 = 011

E = ?[( w12 y1 y2 + w13 y1 y3 + w23 y2 y3 ) + θ1 y1 + θ 2 y2 + θ3 y3 ] = ?0.6

特点：Hopfield网络神经元状态要么在同一“高度”上变 化，要么从上向下转移（能量E减小的方向上转移）。这 是Hopfield网络系统稳定的重要标记。 能量函数的极小值点与网络稳定状态有着紧密的关系。 定理4-1 离散Hopfield神经网络的稳定状态与能量函数E在 状态空间的局部极小状态是一一对应的。 神经网络的能量极小状态又称为能量井。能量井的存在为 信息的分布存储记忆、神经优化计算提供了基础。 应用：将记忆的样本信息存储于不同的能量井，则当输入 某一模式时，神经网络就能回想起与其相关记忆的样本以 实现联想记忆(DHNN的重要应用特征)。

一旦神经网络的能量井可以由用户选择或产生时， Hopfield 网络所具有的能力才能得到充分的发挥。 能量井的分布由连接权值决定。 设计能量井的核心：如何获得一组合适的权值。 权值设计有两种方法： 一、静态产生方法：根据求解问题的要求直接计算出所需要 的连接权值。特点：一旦权值确定下来就不再改变。 二、动态产生方法：通过提供一种学习机制来训练网络， 使其能自动调整连接权值，产生期望的能量井。学习方法 如Hebb规则、δ规则。

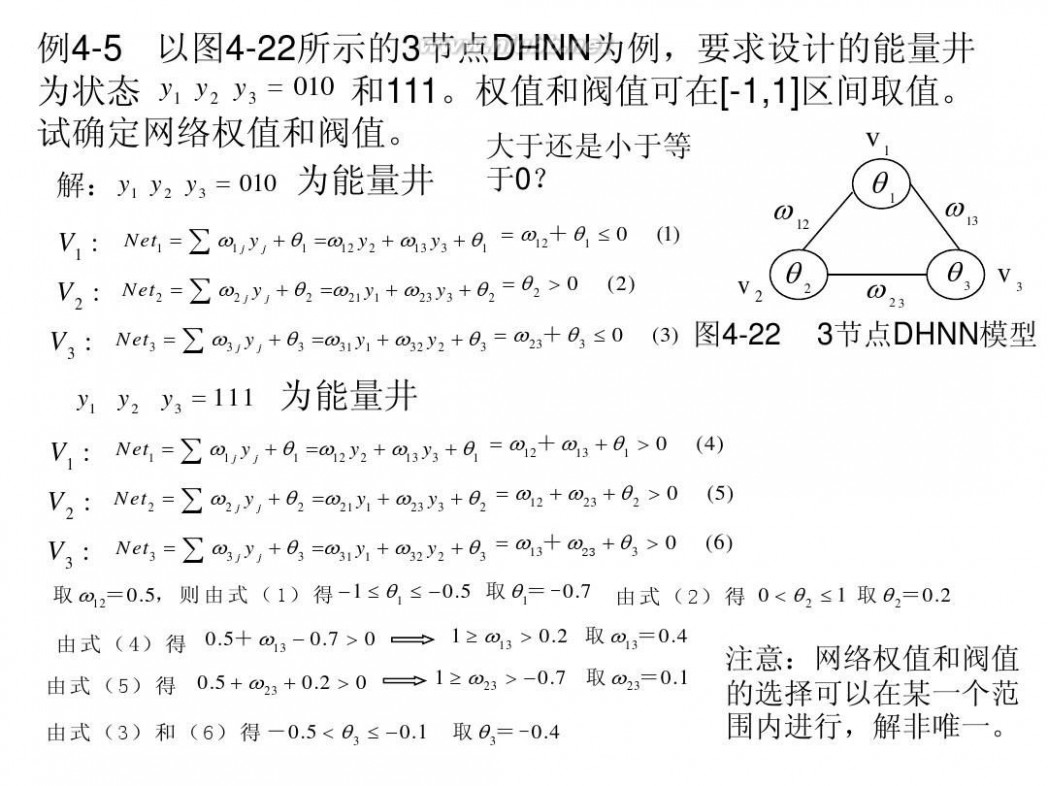
例4-5 以图4-22所示的3节点DHNN为例，要求设计的能量井 为状态 y1 y2 y3 = 010 和111。权值和阀值可在[-1,1]区间取值。 试确定网络权值和阀值。 v1 大于还是小于等 于0？ θ1 解： y1 y2 y3 = 010 为能量井 ω13 ω12 V1 : Net = ∑ ω y + θ =ω y + ω y + θ = ω12＋θ1 ≤ 0 (1) v2 θ2 ω2 3 θ 3 v 3 V2

二 : 人工神经元模型

实际的生物神经工作在电脉冲输入和输出的情形；输入是由“触突”完成的，触突的前面是上1个神经元的输出——轴突，后面是本神经元的细胞体——神经细胞膜；细胞膜和神经元的轴突是相连的，所以1个神经细胞的输出是个一次性的激发过程——输出1个电脉冲；因此，神经细胞膜的动作代表着这个细胞的整体行为，它是在输入不断刺激下，当激发化学成分达到一定程度时的一次“激动”。

1个神经元有许多输入端（当然也有较少的输入，完成中继放大的作用）神经输入——触突，每个触突的大小可以是不同的，也就是它们由接受输入脉冲到刺激本神经元的细胞膜的强度是不一样的。在人为的描述中我们以连接强度——权重值表示（如图中的a，b等等）。

这些由触突连接和电脉冲传递的网络，为了简单人为将他们表示为1个连续的量（如图中的x1,x2等等）。但这种表示与实际还是有差别的。

人为的神经元模型如图所示，输出y可以表示为：

y=a*x1+b*x2+c*x3+d*x4的形式；其中的输入数量（这里为4）认为是输入“信息”空间的大小。但是，如此的神经元如果我们将它们级联许多，其效果如同1个神经元，因为其中只有“线性”的关系。生物在自然形成中具有很好的优化和“智慧”；1个神经元的输出，我们已经说明了，它不是一下子就传递的，是要有积累的，并且输出的脉冲每次也是单一的，有限的；所以实际的神经元的输出对输入而言是呈“非线性”的；在人为的神经元中就是函数f，它是1个非线性的影射函数；它的存在十分重要，它能将有限的输入空间维数加以增加，使神经网络具有识别复杂形状的能力！

1个如下功能的神经元能干什么哪？

y=f（a*x1+b*x2+c*x3+d*x4）

这个例子中选用了四个输入变量（x1,x2,x3,x4）,所以输入空间的维数是4.而触突强度（a,b,c,d）实际上是对这些变量的1个限制。如我们解如下方程，

a*x1+b*x2+c*x3+d*x4=0

我们能知道，变量所在的区域是1个在4维空间中镶嵌的1个“平面”，我们叫它“超平面”（3维空间，比样本空间少一维）。其中这个平面有1个正方向，即平面的“法”矢量方向，以以上［www.61k.com）例子，这个法向矢量就是（a,b,c,d）。

所以1个神经元能够判断输入的变量（x1,x2,x3,x4）处于“超平面”的正方向上，还是反方向上，还是处于这个“超平面”之上；当样本点在“平面”的正方向上，神经元输出为正值，否则就为0和负值；也就是这个神经元是输出1个电脉冲，还是保持不动作。

而神经元的输出经过非线性变形，可以将空间中的样本的复杂性通过层叠的网络加以简化，从而说神经网络在理想意义下可以处理任意的复杂问题。这就是1个神经元和它作用在网络中的功能和模型；但我们可能也注意到真实的神经元是以脉动的电脉冲为传递信息的信号，在一定意义下这样的神经元还处理着“时间”空间的信息，所以生物神经元还具有在时间空间上对问题的优化；而这一点是现代人工神经元欠缺的！

神经元的学习是指对“触突”——连接强度的调整；用最简单的Hebb学习规则即可了；对一组样本集中的每1个样本做如下的调整：

设有n个样本，用i表示其中的1个，x1i表示第1个触突上现在输入的第i个样本值，yi为输入第i个样本时神经元的实际输出；而正确的输出应为Yi，那么本次对第1个触突a的调整量为：

da = r * （Yi -yi）* x1i，

a = a +da

其中r是1个较小的正数。i取1到n，轮流进行学习。学习中r如果很大会出现学习的跳跃，甚至发散；对复杂的问题要用级联的网络，网络中间的神经元数量越多学习的用时就越短；因为神经网络对问题事先是不知道的，中间层的神经元决定的“超平面”全都是随机的；一旦“超平面”趋向问题的解决方向学习就会很快结束。

猴子的智力仅次于人，就是有些重要的网络还没有转到较高的智力结构上；人的智力发育也是如此，小时候的“弱智”，不一定长大就弱，那是因为这些人的神经学习还没有到达“启蒙”期；所以我不赞成小孩从小就强化学习；相对“弱”，也并不等于以后智力不如别人！

三 : 美科学家研制模拟人脑神经元运作方式的新型电脑

传统微芯片中执行计算任务的处理器和执行存储任务的存储器是不同的部分。数据在这两者之间来回传递不仅费时，且会耗费大量能量，大大限制了电脑的性能。

为此，加州大学圣地亚哥分校的理论物理学家马西米利亚诺·迪·文德拉和同事利用既能处理数据又能存储数据的“存储式处理器（memprocessor）构建了存储式电脑。这种设计方案模拟了人脑的组成部分——神经元的工作原理。在人脑中，每个神经元既是处理器也是存储器。

迪·文德拉接受美国趣味科学网站采访时表示：“ 存储式电脑 原型机不仅能有效地解决某类计算难题，还可以利用现有技术制造出来。”

迪·文德拉所说的计算难题是指“NP完全问题”。在此类问题中，人们能很快确认可能的解决方案是否有效，但无法确定最佳解决方案。其中一个典型的例子是“旅行商问题”。在这个问题中，某人必须走遍一份名单上的每个城市，找出一条走遍每个城市后回到起点的最短路径。人们或许能很快找到一条覆盖每个城市的路径，但如不一一尝试，很难确认哪一条路径最佳。

现在，新型电脑内的“存储式处理器”能协同工作并同时找出所有可能的解决方案。而且，新电脑也解决了“NP完全问题”中的子集求和问题。迪·文德拉说：“现在的电脑无法解决的此类问题，新型电脑能更有效地解决。我们还想知道，从此类电脑中获取的知识能否让我们更好地理解人脑的工作原理。”

其实，目前也有科学家尝试利用量子电脑来解决此类问题，但量子电脑通常需在极低温度下操作，而“存储式电脑”则能用标准技术制造并在室温下操作。

不过，迪·文德拉也承认，很难增加“存储式处理器”来对电脑进行升级，或许能制造出采用其他方式解码数据的存储式处理器，以制造出更大规模的“存储式电脑”。

四 : 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

神经元模型 第四章、人工神经元网络模型

本文标题：人工神经元模型图-第四章、人工神经元网络模型
本文地址： http://www.61k.com/1172582.html