一 : 数学问题已知函数f（n）=n^2(n为奇数）-n^2(n为偶数）
数学问题
已知f（n）= n^2 (n为奇数）
-n^2 (n为偶数）， 且an=f（n）+f（n+1），则a1+a2+a3...+a100等于
我的算法是 f（n+1）= （n+1）^2 (n为奇数）
-（n+1）^2 (n为偶数）
a1=1^2+2^2
a2=-2^2-3^2
a3= 3^2+4^2
所以叠加完后，
全部=1^2-(100+1)^2=-10200
可是答案是100，我知道正确的解法，可是不知道我哪里错？
请看你的解法的第一行,设n为奇数,那么n+1不就是偶数了?
所以f(n+1)=-(n+1)^2,而不是(n+1)^2
你明白了吗?
a1=f(1)+f(2)=1^2-2^2=-1-2
a2=f(2)+f(3)=-2^2+3^2=2+3
a3=f(3)+f(4)=3^2-4^2=-3-4
...
a100=f(100)+f(101)=100+101
以上式子都用了平方差公式.然后将右边叠加即可.
真的是100耶,不信你算算..
二 : 已知函数f（x2
已知函数f（x2-3）=lg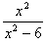 ，（1）f（x）的定义域； （2）判断f（x）的奇偶性； （3）若f [φ（x）]=lgx，求φ（3）的值。 |
解：（1）∵f(x2-3)=lg ，∴f(x)=lg  ，又由 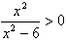 得x2-3＞3，∴f(x)的定义域为（3，+∞）。 （2）∵f(x)的定义域不关于原点对称， ∴f(x)为非奇非偶函数。 （3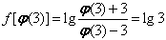）∵  ，∴  ，解得φ(3)=6。 |
考点：
考点名称：函数的奇偶性、周期性函数的奇偶性定义：
偶函数：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）=f（x），则称函数f（x）为偶函数。
奇函数：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）＝-f（x），那么函数f（x）是奇函数。
函数的周期性：
（1）定义：若T为非零常数，对于定义域内的任一x，使f（x+T）=f（x）恒成立，则f（x）叫做周期函数，T叫做这个函数的一个周期。
周期函数定义域必是无界的。
（2）若T是周期，则k·T（k≠0，k∈Z）也是周期，所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期，如常函数f（x）=C。
奇函数与偶函数性质：
（1）奇函数与偶函数的图像的对称性：奇函数的图像关于原点对称，偶函数的图像关于y轴对称。
（3）在公共定义域内，①两个奇函数的和是奇函数，两个奇函数的积是偶函数； ②两个偶函数的和、积是偶函数； ③一个奇函数，一个偶函数的积是奇函数。
注：定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件．
1、函数是奇函数或偶函数的前提定义域必须关于原点对称；定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件．
2、函数的周期性 令a,b均不为零，若：
（1）函数y=f(x)存在f(x)=f(x+a)==>函数最小正周期T=|a|
（2）函数y=f(x)存在f(a+x)=f(b+x)==>函数最小正周期T=|b-a|
（3）函数y=f(x)存在f(x)=-f(x+a)==>函数最小正周期T=|2a|
（4）函数y=f(x)存在f(x+a)=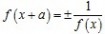
==>函数最小正周期T=|2a|
（5）函数y=f(x)存在f(x+a)=
==>函数最小正周期T=|4a|
对数函数的定义：
一般地，我们把函数y=logax（a＞0，且a≠1）叫做对数函数，其中x是自变量，函数的定义域是（0，+∞），值域是R。
对数函数的解析式：
y=logax（a＞0，且a≠1）
在解有关对数函数的解析式时注意：
在涉及到对数函数时，一定要注意定义域，即满足真数大于零；求值域时，还要考虑底数的取值范围。
考点名称：对数函数的图象与性质对数函数的图形：
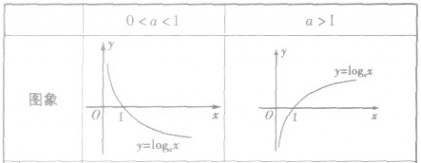
对数函数的图象与性质：
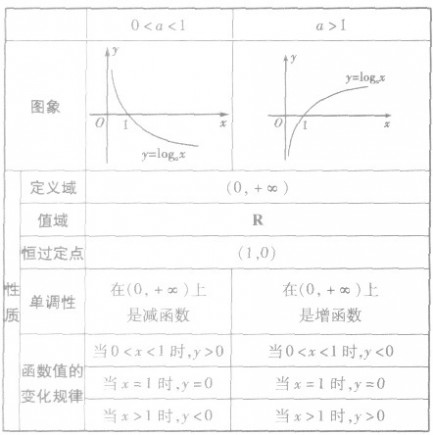
对数函数与指数函数的对比：
(1)对数函数与指数函数互为反函数，它们的定义域、值域互换，图象关于直线y=x对称．
(2)它们都是单调函数，都不具有奇偶性．当a>l时，它们是增函数；当O<a<l时，它们是减函数．
(3)指数函数与对数函数的联系与区别：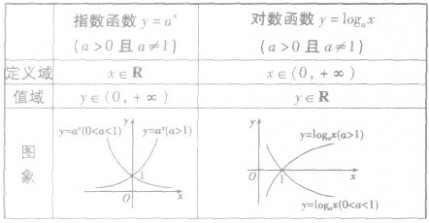
对数函数单调性的讨论：
解决与对数函数有关的函数单调性问题的关键：一是看底数是否大于l，当底数未明确给出时，则应对底数a是否大于1进行讨论；二是运用复合法来判断其单调性，但应注意中间变量的取值范围；三要注意其定义域（这是一个隐形陷阱），也就是要坚持“定义域优先”的原则．
利用对数函数的图象解题：
涉及对数型函数的图象时，一般从最基本的对数函数的图象人手，通过平移、伸缩、对称变换得到对数型函数的图象，特别地，要注意底数a>l与O<a<l的两种不同情况，
底数对函数值大小的影响：
1.在同一坐标系中分别作出函数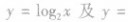
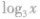的图象，如图所示，可以看出：当a>l时，底数越大，图象越靠近x轴，同理，当O<a<l时，底数越小，函数图象越靠近x轴．利用这一规律，我们可以解决真数相同、对数不等时判断底数大小的问题．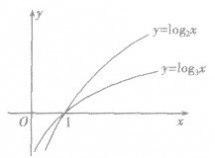
2.类似地，在同一坐标系中分别作出
的图象，如图所示，它们的图象在第一象限的规律是：直线x=l把第一象限分成两个区域，每个区域里对数函数的底数都是由右向左逐渐减小，比如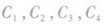
分别对应函数
，则必有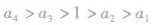
三 : 已知函数f（x2
已知函数f（x2-3）=lg ，（1）f（x）的定义域； （2）判断f（x）的奇偶性； （3）若f [φ（x）]=lgx，求φ（3）的值。 |
解：（1）∵f(x2-3)=lg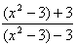 ，∴f(x)=lg 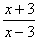 ，又由 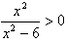 得x2-3＞3，∴f(x)的定义域为（3，+∞）。 （2）∵f(x)的定义域不关于原点对称， ∴f(x)为非奇非偶函数。 （3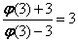）∵  ，∴  ，解得φ(3)=6。 |
考点：
考点名称：函数的奇偶性、周期性函数的奇偶性定义：
偶函数：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）=f（x），则称函数f（x）为偶函数。
奇函数：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）＝-f（x），那么函数f（x）是奇函数。
函数的周期性：
（1）定义：若T为非零常数，对于定义域内的任一x，使f（x+T）=f（x）恒成立，则f（x）叫做周期函数，T叫做这个函数的一个周期。
周期函数定义域必是无界的。
（2）若T是周期，则k·T（k≠0，k∈Z）也是周期，所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期，如常函数f（x）=C。
奇函数与偶函数性质：
（1）奇函数与偶函数的图像的对称性：奇函数的图像关于原点对称，偶函数的图像关于y轴对称。
（3）在公共定义域内，①两个奇函数的和是奇函数，两个奇函数的积是偶函数； ②两个偶函数的和、积是偶函数； ③一个奇函数，一个偶函数的积是奇函数。
注：定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件．
1、函数是奇函数或偶函数的前提定义域必须关于原点对称；定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件．
2、函数的周期性 令a,b均不为零，若：
（1）函数y=f(x)存在f(x)=f(x+a)==>函数最小正周期T=|a|
（2）函数y=f(x)存在f(a+x)=f(b+x)==>函数最小正周期T=|b-a|
（3）函数y=f(x)存在f(x)=-f(x+a)==>函数最小正周期T=|2a|
（4）函数y=f(x)存在f(x+a)=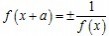
==>函数最小正周期T=|2a|
（5）函数y=f(x)存在f(x+a)=
==>函数最小正周期T=|4a|
对数函数的定义：
一般地，我们把函数y=logax（a＞0，且a≠1）叫做对数函数，其中x是自变量，函数的定义域是（0，+∞），值域是R。
对数函数的解析式：
y=logax（a＞0，且a≠1）
在解有关对数函数的解析式时注意：
在涉及到对数函数时，一定要注意定义域，即满足真数大于零；求值域时，还要考虑底数的取值范围。
考点名称：对数函数的图象与性质对数函数的图形：
对数函数的图象与性质：
对数函数与指数函数的对比：
(1)对数函数与指数函数互为反函数，它们的定义域、值域互换，图象关于直线y=x对称．
(2)它们都是单调函数，都不具有奇偶性．当a>l时，它们是增函数；当O<a<l时，它们是减函数．
(3)指数函数与对数函数的联系与区别：
对数函数单调性的讨论：
解决与对数函数有关的函数单调性问题的关键：一是看底数是否大于l，当底数未明确给出时，则应对底数a是否大于1进行讨论；二是运用复合法来判断其单调性，但应注意中间变量的取值范围；三要注意其定义域（这是一个隐形陷阱），也就是要坚持“定义域优先”的原则．
利用对数函数的图象解题：
涉及对数型函数的图象时，一般从最基本的对数函数的图象人手，通过平移、伸缩、对称变换得到对数型函数的图象，特别地，要注意底数a>l与O<a<l的两种不同情况，
底数对函数值大小的影响：
1.在同一坐标系中分别作出函数
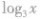的图象，如图所示，可以看出：当a>l时，底数越大，图象越靠近x轴，同理，当O<a<l时，底数越小，函数图象越靠近x轴．利用这一规律，我们可以解决真数相同、对数不等时判断底数大小的问题．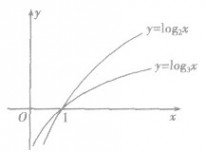
2.类似地，在同一坐标系中分别作出
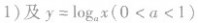的图象，如图所示，它们的图象在第一象限的规律是：直线x=l把第一象限分成两个区域，每个区域里对数函数的底数都是由右向左逐渐减小，比如
分别对应函数
，则必有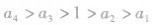
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1