一 : 如何制作课件，探究三角形的面积公式

如何制作课件，探究三角形的面积公式

如何制作课件，探究三角形的面积公式的参考答案

1、通过让学生积极主动地去探索三角形面积计算公式，亲身经历三角形面积公式的探索形成过程，感受转化的数学思想和方法。 2、让学生理解三角形面积计算公式，能正确地计算三角形的面积。 3、通过动手操作、观察、比较，培养学生问题意识，概括能力和推理能力，发展学生的空间观念。 教学重点、难点： 让学生经历三角形面积公式的推导过程，培养转化的数学思想和方法,概括能力和推理能力，发展学生的空间观念。 教学设计： 一、复习. 提问：你知道的平面图形有哪些？（根据学生回答出示相应图形） 我们学会计算面积的有哪些？（板书：长方形面积=长×宽） 师：今天我们一起来研究三角形的面积。 （生：……） 三角形的面积=底×高÷2是我们从书中了解到的，是数学家推导出来的。是依据什么、怎样推导出的呢？今天我们也来作回数学家，利用你们手中的三角形，通过拼一拼、折一折、剪一剪把三角形转化成已经学过的长方形来推导出三角形面积=底×高÷2。 二、动手操作，归纳 1.学生以小组合作的形式来推导公式。 （每个小组有一套三角形学具，包括2个完全相同的直角三角形，1个等腰三角形，1个钝角三角形和1个锐角三角形） 汇报、展示 2、归纳、演示 把一个等腰三角形沿着底边上的高，从中间剪开成两个三角形，（这两个三角形大小相等、形状相同）拼成一个长方形。 拼成的长方形的长就是原三角形的高，长方形的宽是原三角形的底边的一半。所以长方形面积= 高×底÷2也就是三角形的面积。所以三角形面积=高×底÷2，变形后得：三角形面积=底×高÷2 把一个直角三角形的一条高对折后剪开，把剪下的小三角形补在一边，拼成长方形。 拼成的长方形的长是原三角形的底，长方形的宽是原三角形高的一半。所以长方形面积=底×高÷2，也就是三角形的面积。所以三角形面积=底×高÷2 等腰三角形和直角三角形是特殊的三角形，那么是不是只有特殊的三角形才能转 化成长方形从而推导出三角形面积公式，而一般的三角形就不能呢？ 把一个三角形沿着两边的中点对折，然后把两边多余部分往里折，折成一个2层的长方形。 折成的长方形的长是原三角形底边的一半，宽也是原三角 高的一半，所以长方形面积=底÷2×高÷2。而这样的长方形有2个，所以 三角形面积=底÷2×高÷2×2，变形后得：三角形面积=底×高÷2 把2个完全相同的直角三角形拼成一个长方形，长方形的长就是直角三角形的高，长方形的宽就是直角三角形的底。长方形面积=底×高，三角形面积是这个长方形面积的一半，所以三角形面积=底×高÷2 3、教师小结 同学们真了不起，想出了这么多好方法推导出三角形的面积公式。如果用S表示 三角形面积，a表示三角形的底，h表示三角形的高，那么三角形的面积公式的 字母表达式可以写成S=a×h÷2。有了这个公式我们就可以解答有关的题目了。 三、应用 口答下列三角形的面积。练习。（单位：cm） 四、小结 谈谈这节课你的收获是什么？通过学习你能解决什么生活问题？

希望满意！

二 : 三角形面积公式的行列式形式及应用

三角形面积公式的行列式形式及应用

周革生　　福建石狮鹏山工贸学校

从小学到中学，我们学习过好多个三角形面积公式，其中最主要的是

和

，但是当已

又因为

知条件是三角形三个顶点的坐标时，使用上述两个公式就不很方便了，那么有没有更为简单的方法呢？笔者翻阅了许多参考书，找到了下面这个用行列式表示的三角形面积公式，但是始终没有找到这个公式的证明。[www.61k.com)鉴此，本文将应用向量的数量积公式和两直线的夹角公式等知识对该公式进行证明，并给出两个推论和应用实例。

定理：在平面直角坐标系中，已知三角形三个顶点的坐标是Ａ（ｘ１，ｙ１）、Ｂ（ｘ２，ｙ２）、Ｃ（ｘ３，ｙ３），则三角形ＡＢＣ的面积公

因此，Ｓ＝的绝对值。

推论１：在平面直角坐标系中，Ａ（ｘ１，ｙ１）、Ｂ（ｘ２，ｙ２）、Ｃ（ｘ３，ｙ３）　三点共线的充要

例２：判断Ａ（２，３）、Ｂ（１，－３）、Ｃ（３，９）三点是否在同一直线上。（摘自语文出版社的中职《数学》教材第三册Ｐ．１０）

式是Ｓ＝的绝对值。

条件是＝０

证明：由于三角形必有内角为锐角，不妨设∠Ａ是锐角。

把已知点的坐标代入斜率公式和向量的坐标公式可得

推论２：在平面直角坐标系中，过两点Ａ（ｘ１，ｙ１）、Ｂ（ｘ２，ｙ２）的直线方程是

例１：已知Ａ（－３，－２），Ｂ（１，－６），求△ＡＢＯ（Ｏ是原点）的面积。（摘自语文出版社的中职《数学》教材第三册Ｐ．２０）

例３：已知三角形三个顶点的坐标是Ａ（２，１）、Ｂ（０，７）、Ｃ（－４，－１），求三边所在的直线的方程。（摘自语文出版社的中职《数学》教材第三册Ｐ．１０）

行列式的应用 三角形面积公式的行列式形式及应用

２０，３０，４２，……　　＝２

第一递差数列：４，６，８，１０，１２，………　　ｄ１＝４

第二递差数列：２，２，２，２，………　　ｄ２＝２

∴　由

≈５７ｋｍ／ｈ

∴最经济的车速为５７ｋｍ／ｈ，最低费用为

（元）内的唯一解为

点评：根据实际意义，单峰函数在导数为０处取得最值，利用此结论可简化此类题求解过程。［www.61k.com)

６．巧用导数求和

例６：求

证（２）考虑数列：１，９，２５，

（ｘ≠０，ｘ≠１，ｎ∈　）４９，８１，１２１，……　＝１

解：第一递差数列：８，１６，２４，３２，

４０，………　ｄ１＝８

第二递差数列：８，８，８，８，………ｄ２＝８

点评：用导数法求前几项和注意根据待求式的原函数，即由ｆ’（ｘ）去寻找ｆ（ｘ），再求导即可。

证（３）考虑数列：６，２４，６０，１２０，２１０，３３６，……　＝６

第一递差数列：１８，３６，６０，９０，１２６，………　ｄ１＝１８

第二递差数列：　１８，２４，３０，３６，………　ｄ２＝１８

第三递差数列：　６，６，６，………ｄ３＝６

７、求参数值

例７，已知函数在（－

２，＋∞）内单调递减，求函数ａ的取值范围。

解：

，由题意知

在（－２，＋∞）内恒成立，

即恒成立，则

当ａ＝

时，

是常数函数，不在（－２，＋∞）内

符合题意，故ａ＜

三 : 用字母表示三角形的面积公式是（）。

用字母表示三角形的面积公式是（ ）。

题型：填空题难度：偏易来源：期中题

S=ah÷2

考点：

考点名称：用字母表示数用字母表示数：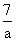
含有字母的式子不仅可以表示数量关系，也可以表示数量。还可以简明、概括地表达运算定律和计算公式，方便研究和解决实际问题。
①含有字母的式子中，数字和字母、字母和字母相乘时，乘号可以记作“·”，也可以省略不写。
②在省略乘号的时候，应当把数字写在字母的前面。
③当“1”和任何字母相乘时，“1”可以省略不写。
④由于字母可以表示任何数，在一些式中，对字母表示数的要运行说明，如：（a≠0）。
⑤因为字母表示的是数，所以在式子中每一个字母都不注明单位名称，计算结果也不注明单位名称，只在答句中写上单位名称。

用字母表示数的意义:
有助于揭示概念的本质特征，能使数量之间的关系更加简明,更具有普遍意义。使思维过程简约化，易于形成概念系统。

四 : (1)证明三角形的面积公式S=；(2)在△ABC中，

(1)证明三角形的面积公式S=； (2)在△ABC中，求证：c(acosB-bcosA)=a2-b2。

题型：证明题难度：中档来源：同步题

证明：(1)S=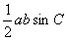， 又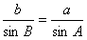， ∴b=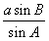， ∴S=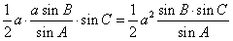； (2)左边=c =右边。

考点：

考点名称：面积定理：S=1/2absinC=1/2acsinB=1/2bcsinA

三角形面积公式：

(1)
，
其中r为三角形ABC内切圆半径，R为外接圆的半径， 。
(2)数量积形式的三角形面积公式：

（3）坐标形式的三角形面积公式：

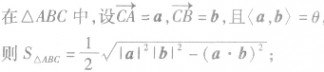
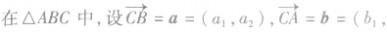
方法提炼:

(1)三角形的面积经常与正余弦定理结合在一起考查,解题时要注意方程思想的运用,即通过正余弦定理建立起方程(组),进而求得边或角;
(2)要熟记常用的面积公式及其变形.

考点名称：余弦定理

余弦定理：

三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍，
即。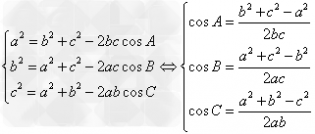

推论：

在△ABC中，若a²+b²=c²，则C为直角；若a²+b²＞c²，则C为锐角；若a²+b²＜c²，则C为钝角。

余弦定理在解三角形中的应用：

（1）已知两边和夹角，
（2）已知三边。

其它公式：

射影公式：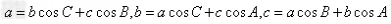

五 : 三角形的面积公式

[www.61k.com] 本文标题：三角形的面积公式-如何制作课件，探究三角形的面积公式
本文地址： http://www.61k.com/1166795.html