一 : 哈雷彗星绕太阳运行的周期是多少？

哈雷彗星绕太阳运行的周期是多少?

哈雷彗星绕太阳运行的周期是多少？的参考答案

哈雷彗星的平均公转周期为75年或76年,但是你不能用1986年加上几个76年得到它的精确回归日期.主行星的引力作用使它周期变更,陷入一个又一个循环.非重力效果（靠近太阳时大量蒸发）也扮演了使它周期变化的重要角色.在公元前239年到公元1986年,公转周期在76.0（1986年）年到79.3年（451和1066年）之间变化.最近的近日点为公元前11年和公元66元.

公转轨道.

二 : 哈雷彗星绕太阳运行的周期约为多少年？

哈雷彗星绕太阳运行的周期约为多少年？

---

哈雷彗星绕太阳运行的周期约为76年

1682年8月，天空中出现了一颗用肉眼可见的亮彗星，它的后面拖着一条清晰可见、弯弯的尾巴。这颗彗星的出现引起了几乎所有天文学家们的关注。当时，年仅26岁的英国天文学家哈雷对这颗彗星尤为感兴趣。他仔细观测、记录了彗星的位置和它在星空中的逐日变化。经过一段时期的观察，他惊讶地发现，这颗彗星好像不是初次光临地球的新客，而是似曾相识的老朋友。

在哈雷生活的那个时代，还没有人意识到彗星会定期回到太阳附近。自从哈雷产生了这个大胆的念头后，便怀着极大的兴趣，全身心地投入到对彗星的观测和研究中去了。在通过大量的观测、研究和计算后他大胆地预言，1682年出现的那颗彗星，将于1758年底或1759年初再次回归。哈雷作出这个预言时已近50岁了，而他的预言是否正确，还需等待50年的时间。他意识到自己无法亲眼看见这颗彗星的再次回归，于是，他以种幽默而又带点遗憾的口吻说：如果彗星根据我的预言确实在1758年回来了，公平的后人大概不会拒绝承认这是由一位英国人首先发现的。

在哈雷去世10多年后，1758年底，这颗第一个被预报回归的彗星被一位业余天文学家观测到了，它准时地回到了太阳附近。哈雷在18世纪初的预言，经过半个多世纪的时间终于得到了证实。后人为了纪念他，把这颗彗星命名为“哈雷彗星”。其实在历史上从公元前240年起的每次回归我国都有所记载，最早的一次可能是周武王伐纣之年，即公元前1057年。哈雷彗星每隔大约76年都会按时回归。在哈雷彗星回归时，可以对它进行大量的观测研究。哈雷彗星的最近一次回归是1986年，中国和各国一样对它进行了大量的观测，发现了断尾现象。它的再次回归要等到2061年左石。

三 : 天文学家观测到哈雷彗星绕太阳运转的周

天文学家观测到哈雷彗星绕太阳运转的周期是76年，彗星离太阳最近的距离是8.9×1010m，但它离太阳最远的距离不能测出．试根据开普勒定律计算这个最远距离．（太阳系的开普勒恒量k=3.354×1018m3/s2）

题型：问答题难度：中档来源：不详

设彗星离太阳的最近距离为l1，最远距离为l2，则轨道半长轴为 a= l1+l2 2 -----① 根据开普勒第三定律有： a3 T2 =k------② 则由①②求得：②彗星离太阳最远的距离是：l2= 3 8KT2 -l1 代入数据得：l2=5.225×1012m 答：彗星离太阳最远的距离是5.225×1012m．

考点：

考点名称：开普勒行星运动定律

开普勒行星运动定律：

1、所有行星围绕太阳运动的轨道都是椭圆，太阳处在所有椭圆的一个焦点上。
2、对每个行星而言太阳和行星的连线在相等的时间内扫过相同的面积。
3、所有行星轨道的半长轴R的三次方与公转周期T的二次方的比值都相同，即常量。
4、常用开普勒三定律来分析行星在近日点和远日点运动速率的大小。

开普勒三定律的对比：

开普勒第一定律：
开普勒第一定律，也称轨道定律：每一个行星都沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点。

开普勒第二定律:
开普勒第二定律，也称面积定律：在相等时间内，太阳和运动中的行星的连线（向量半径）所扫过的面积都是相等的。这一定律实际揭示了行星绕太阳公转的角动量守恒。（角动量在高中学习中不考查）

开普勒第三定律:
开普勒第三定律，也称周期定律：是指绕以太阳为焦点的椭圆轨道运行的所有行星，其椭圆轨道半长轴的立方与周期的平方之比是一个常量。

知识点拨：
近年高考试题中的天体运动问题，试题情境熟悉，多为匀速圆周运动模型，不是卫星环绕地球的圆周运动，就是行星环绕太阳的圆周运动。运算简单，大多数试题直接运用开普勒第三定律进行分析或计算，有些试题则需运用牛顿第二定律与万有引力定律、“黄金代换”等分析计算。

四 : 哈雷彗星绕太阳运行的周期约为

五 : 火星直径约为地球的一半，质量约为地球的十分之一，它绕太阳公转的轨道半径约为地球公转半径的1.5倍．根

火星直径约为地球的一半，质量约为地球的十分之一，它绕太阳公转的轨道半径约为地球公转半径的1.5倍．根据以上数据，以下说法正确的是（　　） A．火星表面重力加速度的数值比地球表面小 B．火星公转的周期比地球的长 C．火星公转的线速度比地球的大 D．火星公转的向心加速度比地球的大

题型：多选题难度：偏易来源：海南

A、根据万有引力等于重力得出： G Mm R2 =mg得：g=G M R2 ，根据火星直径约为地球的一半，质量约为地球的十分之一， 计算得出火星表面的重力加速度约为地球表面的 2 5 ，故A正确； B、研究火星和地球绕太阳公转，根据万有引力提供向心力得出： G Mm R2 =m( 2π T )2R得：T=2π R3 GM ，M为太阳的质量，R为轨道半径．火星的轨道半径大于地球的轨道半径， 通过T的表达式发现公转轨道半径大的周期长，故B正确； C、研究火星和地球绕太阳公转，根据万有引力提供向心力得出： GMm R2 =m v2 R ，得：v= GM R ．M为太阳的质量，R为轨道半径．火星的轨道半径大于地球的轨道半径， 通过v的表达式发现公转轨道半径大的线速度小，故C错误； D、研究火星和地球绕太阳公转，根据万有引力提供向心力得出： GMm R2 =ma，得：a=G M R2 ．M为太阳的质量，R为轨道半径．火星的轨道半径大于地球的轨道半径， 通过a的表达式发现公转轨道半径大的向心加速度小，故D错误； 故选AB．

考点：

考点名称：万有引力定律的其他应用

万有引力定律的其他应用：

万有引力定律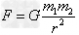：（G=6.67×10^-11N·m²/kg²），万有引力定律在天文学中的应用：
1、计算天体的质量和密度；
2、人造地球卫星、地球同步卫星、近地卫星；
3、发现未知天体；
4、分析重力加速度g随离地面高度h的变化情况；
①物体的重力随地面高度h的变化情况：物体的重力近似地球对物体的吸引力，即近似等于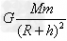，可见物体的重力随h的增大而减小，由G=mg得g随h的增大而减小。
②在地球表面（忽略地球自转影响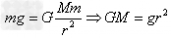）：（g为地球表面重力加速度，r为地球半径）。
③当物体位于地面以下时，所受重力也比地面要小，物体越接近地心，重力越小，物体在地心时，其重力为零。
5、双星问题：天文学上把两颗相距比较近，又与其他星体距离比较远的星体叫做双星。双星的间距是一定的，它们绕二者连线上的同一点分别做圆周运动，角速度相等。以下图为例


由以上各式解得：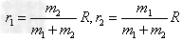
6、黄金代换公式：GM=gR²。

本文标题：哈雷彗星绕太阳运行的周期约为-哈雷彗星绕太阳运行的周期是多少？
本文地址： http://www.61k.com/1165450.html