一 : 第四章
躺在床上,翻来覆去,睡不着,看来这又将是个失眠的夜晚啊。
我不断回忆着鹿晗的眼神。
闭上眼睛,又睁开。
我掀开床被,下了床,准备四处散散,来到房顶,顺着屋檐,找到一个安全的地方坐下,欣赏着首尔的夜空,今天没有星星,我不由得的失望,看向大海的方向,那个望不及,触不及的远方,不禁看得失神…
“为什么不睡觉?”
鹿晗的声音从身后传来,我不由得的看向他,他在我身上搭了一件外套,随后坐在我旁边,我愣了愣,“睡不着”…
他笑了笑,摸着我的头,看着我,“你还是和小时候一样”我有点诧异的看着他,“你为什么不问我为什么回来?”他垂下了头,没有说话。
“或许,你不应该回来”他的嘴角动了动,声音小得可怜,他的话埋藏在风里,吹得无影无踪…
六年级:wulili
二 : 第四章门口风波
“快点啊,快迟到了,开学第一天就迟到那就不想成名人都会成为名人了,”我焦急地说到。
“还不是因为你,走到大街上看什么热闹,害我在大街上找你大半天,不然会这么狼狈啊,等等。。。。。先让我喘口气先,我快没气了。”小丽气呼呼地说到。
“再磨蹭真的要迟到了,别墨迹了。”我抬头望了望校门口的那大钟此刻7:55了,上课时间是8:15。
“真走不动了,你先让我喘口气啊!”
“你这个乡巴佬怎么那么不懂的怜香惜玉呢?是不是找打啊!”一个头发染成五颜六色的人从奔驰车上走了下来说到。
“额,我好像不是说你吧,请问你是哪位?”我特不服气的说到。( 文章阅读网:www.61k.com )
“说你不会怜香惜玉,怎么了,也不知道哪里来的乡巴佬。身上的衣服是哪个垃圾堆里捡来的吧,不会打小你就穿这件衣服吧?”那青年一脸不屑的说到。
“这关你什么事?我的事还用不了你来指手画脚吧,这位同学请你说话放尊重点。”我生气的说到。
“就说你怎么了,你打我啊!来啊,你这乡巴佬,我可是有钱人,你要我尊重你,你是那颗葱。”
“你。。。。。”我握紧拳头
“怎么不敢了,你这土鳖说你了也就说你了,还想要我尊重你,今天我听到最好笑的话了”
“别跟这种人计较,阿龙,我们上去,快上课了”小丽休息一下也恢复了说到。
“好,我们上去吧。”
“咕咕,这女的长的真标志啊,我一定要把她搞上床”青年心里想到。
“美女,怎么称呼啊,我叫秦受,我想和你交个朋友,可以吗?”那秦受一副彬彬有礼地说到。
“不感兴趣,阿龙,走吧”小丽拍拍我肩旁说到,然后就走向教室的方向了。
从背后看去,小丽真的格外的漂亮。
长长的头发在脑后扎成一个马尾,粉色的格子短袖的衬衫,下身牛仔裙,脚上穿着白色的安踏运动鞋,这一身利索清丽的打扮,不但没有影响她的美丽,反而让她充满了青春的气息,同时又有种成熟的味道。
更重要的是,这一身装扮,把她那妖艳动人的身材完美的体现出来了。
在粉色衬衫的包裹下,盈盈一握的蛮腰婀娜多姿,牛仔裙的包裹下,那浑圆的翘臀让人简直不想移开目光。
尤其是那一双修长的双腿,嫩白而充满美感。
我呆呆地望着那背影,一下子出神了。此尤物只有天上有,地上无啊!!!
“喂喂,阿龙,你还不赶紧,你眼睛往哪里看,我脸上还有脏东西吗?”小丽摸摸了一下自己的脸颊。
“那啥,没脏东西了,只是我们青梅竹马已经16年了,以前没发现你那么漂亮”我不好意思说到。
“你这家伙,现在才发现啊!?别灰心,本小姐还没有男朋友哟,你有机会的。”小丽俏皮的说到。
小丽走着教室的方向,只剩下我一个人呆呆的站在原地。心里却有些愧疚,小丽在以前已经多次向自己表明心意了,自己却因为家里条件而一直回避。
其实阿龙不知道,他之所以会这样,一方面是因为16岁正是青春萌动的年龄,看到漂亮的女生,自然会有一些冲动。
另一方面,也是因为随着年龄的增长认识到两个人喜欢跟家里的条件是没什么太大的关系,当然女孩子是拜金的除外,小丽当然是不拜金了,不然还会跟阿龙关系那么好,意识到家庭条件的不重要性,这才可以完全放下心中的包袱。
“阿龙,你这家伙是不算上学了吗?还在哪里傻傻地站着”小丽双手抱着肩膀,让那颇显规模的胸脯高高额隆起,让阿龙心里忍不住狂跳几下。
“好,我知道了,我马上就来”马上回过神回答到。
“快点,快迟到了。”
我们马不停蹄地跑到教室门口,气呼呼看了教室,大部分同学已经坐好位置了,看看了看看讲台,心里暗叹到:还好老师还没有来,不然就丢人丢到姥姥家了。
一进教室傻眼了,前面的好位置已经坐满了,只剩下一个在中间的座位了,我心里想到,还是让小丽坐中间的好位置吧,我立马走到最后的没人的坐的位置,刚坐下,小丽就笑眯眯地向我走来。
“同学,坐这里吧,这个位置好。”那男同学指着中间的位置说到。
“谢谢了,我不喜欢坐在这里。”小丽微笑的说到,然后走到我旁边坐下。
“你没发烧吧,我这里是全班最后面的座位啊,你成绩那么好坐到这里干什么。”我惊讶地问道。
“你这个省状元都在这里坐着,还有你说的成绩好,在你面前我可不敢说我成绩好,只有你妖孽才算的上尖子生,七科老师才扣了你两分,再者说我答应大年说要照顾你的”小丽狡诈的说到。
“额,我想低调点,别给我整高调了,再说美女坐这里你不是让我成为全班的公敌吗?”我苦笑说到。
“我才不管他们怎么想,我坐这里我乐意,怎么着,再说你想低调,老师点名的时候,你想低调都没办法低调了,叶子龙这个名字在全省现在已经是一个妖孽的代名词了,你还想低调?”
“好吧,你赢了,你爱怎样就怎样吧”我无奈地说到。
“本来就是,本小姐要怎么做你管不着,你刚才是不是想追我啊,我坐在这里不是更有利于你吗?近水楼台先得月嘛。不过我们现在都是学生,学业才是最重要的,说不定等过几年以后再回头看,就会发现现在其实很好玩,很多事也很多事情也是很幼稚”小丽眨眨眼睛说到。
“我明白的!”阿龙也笑了笑,既然小丽都如此放得开,他也平静下来了,洒脱说到“我明白你的意思,其实我也觉得现在学习最重要,如果现在不好好学习,将来一定会后悔的!”
小丽顿时嫣嫣一笑,道:“阿龙,你能这样想就最好不过了,我承认我一直都是喜欢你,或许刚才你才意识到你也是喜欢我的,我自恋一点哈。但是我希望你不要因为这事影响了你的学习,以后我们相互帮忙。”
“荣幸之至”阿龙微笑道。
小丽顿时嘻嘻一笑,令百花失色,美丽之至。
阿龙也跟着笑起来,只是他的眼神很清澈,就好像天空的星辰一样,让人沉迷。
小丽跟阿龙是多年的同学朋友,但是阿龙的家里到底是怎样的却不是知道多少
小丽看着心中心中微微一震。
本书首发来自17K小说网,第一时间看正版内容!
三 : 第四章Volterra模型
第四章 Volterra模型
在本章中,我们首先回顾最常用的非线性建模方法.第4.1.2节讨论多项式Volterra模型建模方法的特性,第4.2节详细解说记录下来的完全电非线性和电热非线性,以及建模非线性级数展开中所用的项.4.3节描述了如何应用Volterra分析方法计算一个普通发射放大器的失真,并且作为第一个研究案例,第4.4介绍了在一个BJT CE放大器中,影响IM3失真的所有项的分析.同样的分析(对一个MESFET放大器)在第4.5节中介绍.
4.1非线性建模
为了能够分析功放的非线性行为,我们需要为实际的非线性电路,无源匹配以及偏置元件建立精确的模型.但此模型的获取又有一定难度.众所周知,N阶失真的数量与I-V和Q-V波形的N阶导数成比例(参照[1-3]).因此,为了达到精确的失真模拟,对有源元件的I-V和 Q-V波必须建模,因此不仅是直流值,高阶导数同样是正确且连续的.(为了便于参考,在早期的仿真模型中,第一阶导数可以不连续).此外,电容是很容易建模的,因此电荷没有存储,这将导致完全容性结点的非物理整流和自偏压.因此,特别是如果电容值同时取决于两个终端电压,将电容模拟等效于电荷平衡是十分重要的[5].
由于无源元件在高频具有分布特性,很难在射频频率上对其建模.有损耗的传输线难以在时域上进行建模,一般而言,无源元件的建模在频域上更加精确.尽管如此,有些无源元件的频域仿真模型在高次谐波时也可能是不准确的,例如传输线宽上的阶跃变化,在电路分析中,可以采用测试电路的标准终端阻抗值来进行分析. 简而言之,为了得到精确的失真模拟,从模拟模型中需要:
1. 对N阶失真模拟来说, I-V 和Q-V波形的N阶导数必须足够精确.
2. 结点阻抗的频率响应对于最高相关谐波,必须是正确的.同时,在基带频率,偏置阻抗和热阻抗的正确模型也是十分需要的.
3. 如果可以得到主要失真源的组成信息,将十分有用.
4.1.1非线性仿真模型
通常来说,功放和发射机设计师使用两种非线性模型:一种是用于系统仿真的行为黑盒子模型,另一种是用于电路仿真的器件模型.根据建模方法的不同,可以对这两类模型进行更深层分割:可以是解析的,基于一些预先确定的和物理学的用参数表示的模型函数,或者完全根据实验的,将测量数据列表并以内插值替换的,或者用简单的曲线或物理意义不清楚的多项式表示的模型.在表4.1中有所介绍.
表4.1 功率放大器的非线性模型

行为基带模型广泛用于模拟和优化整个发射机和收发器,并且增加了新的功能,例如模拟记忆效应,在[6]中介绍.然而,行为模型描述的或者是一个已经存在的放大器,或者行为模型源自到目前为止不存在的放大器规范说明,但是在设计一个新的功率放大器中,行为模型的使用遭到限制.
这里简明地介绍了最常用的行为模型的特性,仅用于参考.简单的静态的AM-AM 和 AM-PM波形不能够模拟记忆效应,但是基于调制频率的AM-AM和AM-PM波形的模型已经被开发出来.如图4.1所示,在Saleh模型中, AM-AM和AM-PM非线性模块的输入和输出端都增加了线性滤波器.在Blum 和Jeruchim(在[7]中描述)模型中,用快速傅立叶算法及足够的抽样来找到用于修改AM-AM表的瞬时调制频率.有一种Volterra型的行为模型被称作Volterra输入输出图(VIOMAP).它是普通S参数的非线性的概念性扩展,包括谐波响应,并且被成功应用于单音负载下拉仿真中[9,10].

图4.1 (a)功率放大器的AM-AM和AM-PM波形
(b)基于滤波器和无记忆非线性的由频率决定的非线性模型.
器件模型描述了半导体设备的动作,以及无源和分布式元件的合适模型,可以建立并优化功放的模型

.
早期的半导体模型是解析的,所采用的等式首先来源于半导体物理学,然后将其简化以减少仿真时间.这些基于等式的模型的一个基本问题是,所选用的函数和控制参数固定了I-V 和Q-V特性的可能形状,并且可能没有足够的自由度来模拟例如IC-VCE曲率.例如,在基本的Gummel- Poon (GP) BJT SPICE模型中,集电极电流的简化形式如下:

其中, 基本的指数仅可被三个控制参数修改: IS依比例决定电流, VAF (所谓的早期电压[12], 如图4.2所示)构成输出电导的一个极其简化的模型, IKF (所谓的拐点电流)降低高电流时的增益[13, 14].这个简单的等式涵盖了整个I-V平面,同时固定了导数dnIC/dVn,因而固定了非线性行为. SPICE GP模型可以适当地用于模拟基带信号[15],但是特别是对于过分简单化和固有性线的输出阻抗模型, 不能用SPICE GP模型进行精确的失真仿真,这将在本书后面说明.
更好的物理模型已经被开发出来,比如BJT的Mextram和VBIC ,以及用于LDMOS的摩托罗拉MET模型,这都是久经考验的模型.与早期的SPICE模型其比,这些模型的性能大大地提高了.后者对于找到正确的直流偏置十分重要,这是因为自我加热使得I-V波形产生一个大的差值.假如热模型有足够的时间常量来模拟缓慢加热包(主要影响直流偏置和芯片表面的微秒范围热记忆),后面的模型也可用于模拟热记忆效应

.
图4.2 在BJT中使用早期电压VAF模拟输出阻抗
模型的额外自由度增加了其复杂性以及控制参数的数量.在一个极限中,MOS BSIM模型有数十个参数来单独控制比例特性.因此,模型的复杂性趋于失控,并且其配置愈加复杂,对错误愈加敏感.
另一种设备建模的方法是放弃等式,而采用列表的测试数据或者完全根据实际以验的函数来代替.现在,任何形式的I-V和Q-V特性的模型可以被建立,这是通过Root模型得到的方法,称作” 设备最了解”模型[5].在内插列表数据时,存在一些技术问题,这是因为内插的多项式容易使数据点之间产生振荡,因此派生出高阶非物理波动.然而,由于预定函数不需要压力,列表模型使用灵活.
Volterra模型是一种经验模型,它不依赖于半导体物理学.其非线性描述为多项式,系数可以通过对I-V和Q-V函数微分得到,也可通过将多项式直接填入测量数据表里得到.在此我们使用的是后者,在接下来的章节中,我们将会更深层次地对Volterra模型的特性进行研究.
4.1.2 Volterra模型的特性
多项式模型并不自动地对模拟快速响应,相反,它可能严重地会聚在高于原始设置范围的信号电平上.然而,多项式模型允许使用高效的Volterra分析程序.
然而,采用Volterra模拟方法的主要动机并不是看中了其速度优势,而是它能提供一个极好的分析工具来进行分析.主要的失真机制可以用与在普通交流噪声分析中采用的相同的方法来进行分析,由于非线性分析,多重的混合机制同样可被识别,例如可以帮助谐波终端阻抗的设计等.因此, Volterra分析是少数可以帮助理解记忆效应和帮助设计优化的方法之一.
尽管如此,仍需承认多项式模型存在一些缺点.首先,多项式模型要遭受在适宜的带宽范围外,其响应接近无穷大这一事实.传统的非线性建模函数与此正好相反,它在整个偏置范围内平滑,有限的表现是我们设计的特性,因为它帮助使信号收敛,并且信号摆动不必要进行推理的了解.因此, Volterra分析并不是一个非常普通的工具.由于速度原因, Volterra分析被用于快速失真分析和模拟器中的低噪放型小信号电路(例如Voltaire XL [22] 和SPICE的早期版本)中,或者甚至做为独立的模拟器使用[23]. 然而,为了功放能被成功地进行分析,可靠的早期信息仍是必需的.
第二, 预先得需要实际的大信号直流偏置电压.大信号动作经常会引起直流工作点的移位,它同时影响增益和非线性的数量.此信号感应引起的直流移位会减缓谐波平衡模拟中收敛的速度,并且在非反复Volterra计算程序中,只能对它进行估计,而非完全地预测.为了克服这点,我们需要检查直流移位是不是很大,或者在实际的大信号工作点使得多项式模型合适.
第三,在多项式函数的装配中,需要知道输入和输出电压摆动的范围.多项式模型的实际功率是除开失真成分的其它部分.适宜的范围越大,低阶多项式的精确度越小.因此,沿着最大信号振幅安装是合适的,为确保多项式模型的精度,不能太超过此范围,并且由于多项式响应可能在合适的范围外是完全非物理的,也不能超过一个较小的范围.在这种情况下,就需要对输入输出轨道有较好地评估.总之, Volterra分板并不是一种简单使用的独立的仿真方法,但当它用在与其它仿真方法(例如谐波平衡)并联使用时,此方法提供了更多调试功能.
在本书中,研究的案例仅限于单级晶体管放大器,并且对Volterra分析半解析地计算(象征性地来源于每一个失真源到所有结点电压的转移函数). 象征性的分析并不是必需的,它限制了对CE或CS放大器固定的结构以及双音测试信号的分析.而Volterra分析却能达到,通过在(用标准修改结分析矩阵以及非线性电流源表示的)任何电路上运用通常非线性交流分析方法.
4.2非线性I-V和Q-V特性
大多数的晶体管模型是以Π模型或T模型为基础.这里使用的是Π模型,本节中描述了用BJT,异质结BJT(HBT)和场效应管(FET)的Π模型表示的典型传导(I-V)和电容(Q-V)的非线性特性.在这里将BJT作为一个案例,但同样的模型也可用于FET晶体管,只是多项式系数设置不同.
前面已经讲过, Volterra模型是以I-V和Q-V曲线的多项式建模为基础.测量这些曲线也许会有些困难,详见第五章.这样的电荷不能直接进行测量,我们必须依靠交流测量的电容以及对所得电容值得到的电荷等式求积分.用类似的方法,I-V曲线可以通过由S参数测量得到的

一个更安全的出发点. 和值进行大部分重造,但是实际的I-V曲线是
这里介绍的模型是电热模型,这意味着其结温是一自由变量.然而,直流温度上升包含在偏置点中,并且只考虑由动态自我加热引起的温度变化.由于功耗是电压和电流的产物,我们认为结温中的交流成分已经是一个二阶现象.因此,一个三阶的模型仅仅包括温度的一次方,这意味着电容元件的温度依靠性被认为是线性的.
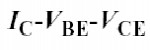
4.2.1 特性
在大多数被报导的BJT/HBT Volterra级数分析中,集电极电流被认为只是基极电压的函数[25-27],此考虑方法抓住了主要指数的输入输出非线性但是认为输出电导是常数.在MESFET Volterra级数分析中,漏电压的效应通常用
实现, (参照[28]),但即使如此,也难以捕捉所有的非线性特性.
在(4.1)式中,等式

是

,和结温T的一个三维简单函数,就像的一个多项式来
.通过扩展大信号I-V函数
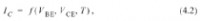
到一个三输入的泰勒级数(在直流工作点
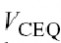
,和周围),很容易得到一个多项式模型.因此,交流电流的电热三阶级数展开可以写作
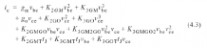
:
其中,
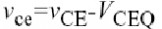
元素xxx的i阶非线性系数.(

第一行只受影响,

第二行只受,, 并且Kixxx是).由等式可见,可以用来标志影响(例如非线性输出电导).尽管如此,第三
行又列出了的温度变化. 和的向量积.最后,第四行列出了与两个终端电压混合在一起图4.3中证明了电非线性的影响,其中,绘制了在三个基极电压处的集电极电流,它是三个不同基极电压处集电极电压的函数.如果除外的所有系数都是零,我们可以得到如图4.3(a) 所示的三条等间距的水平线.由于线精确地保持水平,输出电导为零,且集电极电压不影响电流数量.此外,由于线之间等间距,跨导是线性的.然而,如果导是非线性的. 或偏离了零,在I-V平面的线距离将会变得不等,这表明跨

图4.3 证明集电级电流非线性.垂直的轴是集电极电流,水平轴是(a)线性响应(b)非零 (c)非零 (d) 非零
非零 (e) 非零电压. (f) 图4.3(b)证明了的影响,

仅仅存在和.与图4.3(a)相比,图4.3(b)中
的线有一个非零的斜率,它与

成比例且不依赖与.
图4.3(b)仍是完全线性的, 图4.3(c)证实了输出电导的非线性,其电流的斜率随而变化.在这种情况下,

仅有一个非零值,
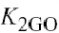
和可被用于模拟输出电导的曲线效应,例如饱和和击穿.
图4.3(d-f)分别图解说明了
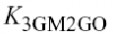
,和的截项,它模拟了基极和集电极非线性物性的交互作用.为了帮助比较,图4.3(d-f)中的稍细线是临摹图(c)的(
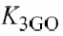
和都有非零值).

(对应于
项)在图4.3(d)中是非零的,这是由于其线的斜率变化不仅仅受图4.3(c)中集电极电压的作用,也受基极电压的作用.这对于图4.2所示的模拟早期效应是十分必需的.相似的推理也可应用于
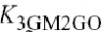
确定输出电导的形状,分别是
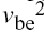
和和的函数. ,如图4.3(e, f)所示,
图4.4对不同建模方法的I-V曲线做了更多的比较.如果集电极电流被模拟为基极电压和线性的一维函数,就产生了一条直的I-V线,如图4.4中细虚线所示.用SPICE Gummel-Poon模型模拟的I-V曲线同样也是直的细的线,但是其斜率和输出电导随集电极电流变化,如图4.2所示.实际上,由于准饱和和截止影响,在大信号或半大信号的情况下,BJT的I-V曲线决不是直线.曲率可以通过使用和的一维多项式模拟,如图4.4中粗实线所示.然而,初步的现象(例如早期效应)在没有引起斜率决定于的值截项时不能被模拟.如图中粗虚线所示,并对应于
(4.3)的完全级数展开.饱和和截止的开关同样取决于基极电压,这使得截项的使用强制地避免了I-V平面角落处的重大误差,如图4.4所示.

图4.4 三个Volterra模型和Gummel-Poon SPICE模型的I-V特性
最后讨论了集电极电流的电热效应,如(4.3)中最后三项所示.在图4.5(a, b)中,描述了一个二次项
不能由小信号参数,它模拟了电流中由温度决定的移位.值得注意的是, 和得到,相反的,需要实际的电流测量. 是一个包含温度和集电极电压影响的三次项,如图4.5(c)所示.它在本质上模拟了温度对输出电导的依靠性.同样的,如图4.5(d)所示,
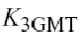
度和基极电压的结合效应.由于曲线的斜率反应了跨导,
度影响的跨导的一个变化. 模拟了温可被认为是受温

图4.5 电热非线性系数的影响. 非零
轴.(c)非零 影响(d)非零影响
在(a) 轴(b)
特性是FET型晶体管中唯一重要的传导性非线性.在BJT中,存在另外
的两个非线性:由指数

引起的非线性和非线性.电导的影响通常更重大,并且也容易模拟.理论上, 等式可以粗略地用电流增益β除,但可用一些方式简化.由于基极电流并不是强烈地依赖于集电极电压,我们可以用一个仅由和决定的两维模型
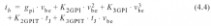
:
这里,系数与之前有着相似的含义.线性项通过进行模拟,

和
模拟其指数曲率.此外

, 可以看成线性
本征基极电阻模拟了由自我加热产生的移位, 项的温度依靠. 较难模拟.它是内部基极点和外在基极点之间的串联电阻,
值.因此,它可以模拟为一个由
和结温控制的三维电
和它的值取决于基极区的电流拥挤,也取决于内部电阻器电压

(导.所有的),内部基极电压

K项(k=1,2,...)都是零,

但是电流拥挤效应是用间的截项模拟的,如(4.5)所示.不论如何,
一个线性电导

. 通常较小,且在下面例子中被模拟为
4.2.3电容模型
如前面解释,将电容建模成多项式电荷,然后将其关于时间进行区分以得到位移电流.电荷可能并且经常是由多于一个的端口电压所控制,这使得我们必须使用一个类似于(4.3)的多维多项式.电荷同样可以模拟为一个电容,在这种情况下,电荷不出现在控制结点之间,而出现在一些其它的结点间.在下面的例子中,只假定了一个控制电压,式(4.6)描述了基极到发射极的电荷,它是基极到发射极的电压以及温度的函数

.
从这个等式中,可以轻松地得到对应测量电荷Cpi和非线性电流源
需将电荷等式(4.6)分别关于和时间进行区分即可. .只
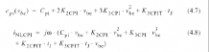
在(4.8)式中, ω仅是失真音调的频率;因此,电容并不会引起直流失真电流但是在谐波频率处失真最严重.等式(4.7)指出由温度决定的电荷项K2CPIT不能来源于电荷测量;尽管如此,一个时变的结温可能引起一个与它成比例的电流.另外, (4.6)式中的第一项Cpi描述了小信号电容, K2CPI和K3CPI定义了它的有关电的非线性. K3CPIT描述了是控制电压和结温函数的电荷,由于C = dQ/dv, K3CPIT的作用可以看成是电荷值的温度决定性.
如(4.6)所示,一个线性的C-V趋势K2CPI引起了二次电荷非线性.同样的,与v2 (K3CPI)成比例的电荷引起立方的非线性.不同类型的电容有着不同的特性,如图
4.6(a)所示.如 (4.27)所示,基极-射极电容Cpi是指数的,因此它是高度的非线性的.BJT和FET中有偏的P-N结或肖特基结仅是稍微的非线性,它们可以通过增加反偏压进行更深一层的线性化. MOSFET型晶体管有着特殊的栅电容,例如, CGS在门限电压的周围dip.如果MOSFET动作接近于关断,此dip会引起大量的二阶非线性.
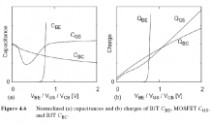
图4.6 (a)归一化的电容(b) 和的电荷
4.3共射极BJT/HBT放大器模型
现在我们使用直接的方法来计算一个共射极BJT/HBT放大器的IM3成分,使用第
2.5.2节所列出的步骤.这样进行分析:首先为电路建立一个模型,通过一个线性的交流分析建立基本的幅度.然后,通过使用第4.3.2节所示的步骤计算二阶电流电压以及三阶电流电压.
4.3.1线性分析
图4.7所示的是一个共射极BJT放大器,它包括输入阻抗ZIN(混合匹配网络和偏置电路),基极-射极电导gpi和电容Cpi,反馈电容CBC,输出电容CCE,输出电导导跨,负载阻抗ZL以及发射极阻抗ZE.输入和负载阻抗不仅包含匹配网络的阻抗,也包括偏置网络和包寄生的阻抗, ZIN由前级的输出阻抗和本征基极电阻rbb组成,如图4.7所示.
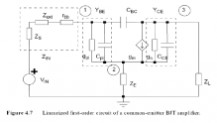
图4.7 共射极BJT放大器线性化一阶电路
为减少等式的数量,输入电压源可以用诺顿等效源来代替

且用下列简化符号

通过替换图4.7中所有阻抗并在结点1至3应用基尔霍夫电流定律,可以得到如下矩阵等式.

通过使用Cramer法则,可以得到结果以及对和集电极的电压如下所示

: 的响应.因此,在基极,发射极
导纳矩阵的行列式写作

:
基极到发射极,

集电极到发射极的电压分别是.最后,

由于成分产生的失真,很容易得到它们的比值: 和经常用于计算失真,例如由gm和

线性化分析的目的是为了获得所有非线性元件的基本电压幅度,这样我们就可以继续计算这些元件内部产生的非线性电流.在此之前,我们需要对信号摆动进行一些观察.
BJT的指数响应是极端的非线性,并且在没有过度失真的情况下,不能承受高于10到30 mV的信号幅度.这听起来不像一个功率放大器,但是两件事情恰好帮助改变此情况.首先,器件并不是完全指数的,但是当驱动到高注入时,BJT线性化可用(4.1)中的参数IKF来模拟.第二,放大器有一些反馈机制来减小BE结中的信号电平.串联发射极阻抗引起一个线性化的串联反馈,CBC引起一个并联反馈.CBC的作用十分重大,这是由于强烈的电容性反馈降低了基极阻抗,因此也减小了BE电压摆动和从驱动激励产生的失真数量.
4.3.2非线性分析
在本节中展示了一个CE BJT放大器的非线性模型,并由它得到IM3失真.该电路有三个两输入和一个三输入的I-V和Q-V非线性,通过鉴定7个一阶系数,二阶系数和三阶系数模拟得到,其中18
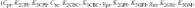
个是电系数
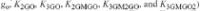
,其它9
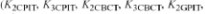
个与动态温度变化相关
.
最后,此分析将介绍IM3音调,它是一个矢量和,由以下组成:7个由立方电非线性引起的项,21个由级联二次方非线性(修正包络信息向上转换到IM3中)引起的项,21个二次谐波向下混合到IM3的项,最后,5个立方的和24个级联的二阶电热项.这些看
起来也许很多,但它描述了产生失真的不同机制的真实幅度;它同样清楚地证明了,只要立方项是解析的,大量的信息就会失去.若电路较大,分析的阶数越高,则需要对数据进行压缩,但是原理还是一样的:我们希望知道,通过从直流或谐波波段混合失真并使总失真最小化(或最小化其记忆效应),能产生多少IM3总数;我们希望知道在这些谐波波段,由失真电压引起了什么样的非线性和实际阻抗.
由于项数众多,我们不单个地对这些项进行讨论.完整的分析见附件C,接下来用一些例子讲述计算步骤.
4.3.2.1二阶失真电流
图4.8所示的电路用于解决二阶响应,图4.7中的线性输入电压在此被短路, 添加二阶失真电流源与所有非线性电路元件并行.以T结束的电流是电热电流,将在第4.3.2.5节中讨论.如同以前, ZIN, ZE和ZL将包寄生,偏置阻抗和匹配阻抗结合在一起.
为了计算自我加热效应,瞬时功耗用
热阻抗用于计算频率ω2–ω1
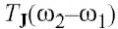
处的瞬时温度波动计算,第3.4节所示的.可以对不同的电路元件使用不同的温度,但是它们在物理上靠近基极区,此处使用共同的温度.然而对于大型设备,将此设备分成较小的并行设备是十分有利的,这样可以看出不同的温度变化.

非线性被模拟为和,和温度组成的三维函数,它包括和是基极到射极电压和非线性以及所有高达三阶的交叉项. 温度的函数,非线性由集电极到基极电压和温度控制.

图4.8 含电流源电路的二阶响应表示 我们通过计算二阶失真电流
ω2–ω1处由开始进行分析.举一个例子,在引起的二阶包络电流是:使用表
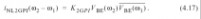
2.5
举另一个例子,

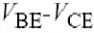
由非线性引起的二阶包络电流是

:
它结合了二阶输入非线性
入输出交叉项,
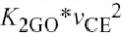
输出非线性的作用,见I-V模型(4.3). 和输从表2.5中可以看出,相量频率和可能的常量项值的选择取决于音频:例如,
的乘积在2ω1处产生一个音调.上述的相量音调被选中,所以
能在包络频率ω2–ω1产生失真.计算基频ω1和ω2的相量(4.12)-(4.14)式. 和用
4.3.2.2跨导倒数转移函数和二阶电压
接下来,我们需要把不同结点的失真电流转换为失真电压.此处,我们选用了一个象征性的分析,因此很容易得到从结点X和Y到结点Z之间的非线性电流源的转移函数。大概的想法是:在每个非线性元件中,失真电流的幅度用较低阶的电压相量计算,并使用转移函数,然后在所选择的结点上,所产生的失真电流被转换为失真电压. 转移函数可从(4.11)中得到,
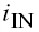
只需将
例如, 转移函数的形式为
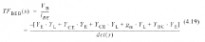
: 用结点X和Y之间的一个测试电流源代替即可.
det(s)由(4.15)得到.附件C中给出了一整套转移函数.通过使用这些符号,基极结点处完整的二阶包络电压为:
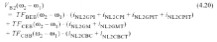
其中,每一个失真电流源乘以合适的跨导倒数(在基极将电流转换为电压).同时需注意,式中有8个不同的电流源(基中的4个是电热的电流源,用T标识),每一个电流源都有一个等式,类似于(4.17) 或(4.18).
为了解决二次谐波电压,
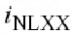
我们需要将需要的谐波的源的电流等式重写,并在相对频率下重新计算(4.20)式.在此步骤之后,基本包络和二次谐波音调是八个
不同成分的总和.通过对这些成分分别存储,我们可以看出哪个是主要的,哪些互相抵消.
4.3.2.3 解三阶电压
接下来,我们要计算IM3在频率为2ω1–ω2时的集电极电压.三阶分析采用与二阶分析完全相同的等效电路,集电极电压用下式计算

:
其中,音调2ω1–ω2的失真电流被计算, 转移函数(同样在2ω1–ω2频率点计算)被用来将X-Y端口的非线性电流iNL转换为集电极电压.然而,与二阶分析相比,非线性电流源的等式更加杂乱,这是由于IM3电流不仅由立方非线性引起,同样由级联的二阶非线性引起.例如,根据表2.6,IM3电流中出现的包络电压和二阶谐波是由非线性引起的
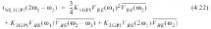
.
相似的响应也会产生,
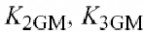
例如通过系数对非线性的
下列的附加项:
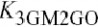
.除开这些之外,

输入输出交叉项给, 和 和带来
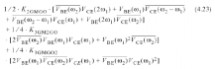
其中,所有线性和二阶输入输出电压的结合如上式所示,且它们的产物在2ω1-ω2处形成一个音调.注意到,在交叉项中,所有可能的排列是必要的.例如,等式(4.23)中的最后一项由在频率ω1, ω1和–ω2处的一个VBE和两个VCE电压组成, 它们可以排列成下面的三个结合: (VBE(ω1), VCE(ω1), VCE(–ω2)), (VBE(ω1), VCE(–ω2), VCE(ω1)), and (VBE(–ω2), VCE(ω1), VCE(ω1)),其中,前面的两个的结果相同.数字频谱卷积可以自动地给出所有的组合.
现在,根据基本结点电压和二阶结点电压来描述IM3.接下来,我们更深一层地讨论失真,失真仅作为基本输入电压的函数.这使得表达式变得十分复杂,但也带来了一个好处,就是能维持二阶失真电压的原始信息.
4.3.2.4 IM3仅表示为基本输入音调的函数
为了将失真仅表示为输入音调的函数,我们需要做两件事.首先,


写作
,TF可由(4.16)和附件C得到.其次,将所有的二阶音调根据基本输
入写出来,这会产生总共42个级联的二阶项,都列在附件C中.
(4.21)式的纯立方部分根据
表2.6,作为

一项被
被
表示为和被写入到(4.24)式中.在此,非线性电流根据的函数被写出来.例如, (4.24)的第的乘积所控制.

输入非线性值所控制,交叉项被输入和输出电压所控制.
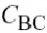
对于. , ,电压和仅必须被


由级联的二次电非线性引起的IM3等式变得十分复杂,整个的等式包括21项从包络得到的混频产物,21项从二次谐波得到的产物,如附件C所示.这里列举这样的一个例子,由K2GM*K2GPI引起的双重混频.组成如下

:
此等式包括两种低频混频结构,如图4.9所示.图4.9(a)描述了第一种结构, 在
中,

ω1–ω2,然后通过
电压和和的乘积在集电极和发射极之间产生包络电流,被转回到基极到发射极电压.这些包络电压和基本在中再次混合,在基极和发射极间
,它们被转换为集电极电压.
和在K2GPI的2ω1–ω2处产生IM3电流.通过转移函数第二种结构如图4.9(b)所示,可以这样解释:
基极直接产生包络电流ω1–ω2.此电流在基极和发射极之间的部分通过
被转换为基极到射极的电压,因而产生的包络电压与基本基极到射极电压在中进行混合,因而在集电极和发射极之间产生了IM3电流.最后,该电流
通过被转换为集电极电压
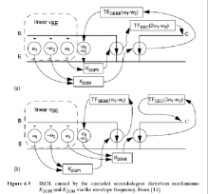
.
图4.9 通过包络频率,由级联的二阶失真结构K2GPI和K2GM引起的IM3L 诸如此类的多重混合产物实在是常见.例如,在AB或B类放大器中,引起IM3的一个主要原因是:当消波不均匀时,晶体管会在输出产生一个高的二次谐波(由高
来模拟).由于二次谐波的频率很高,通过CBC回到输入能很容易地耦合,并且在
称为中与基波再次混合,导致输出端直接有IM3电流.这种结构(在附件C中项)能通过衰减集电极或基极的二次谐波来将其最小化.
4.3.2.5电热项
最后,描述了三阶电热失真结构.
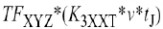
这由三阶项和级联二阶
项组成,其中,热感应二阶失真与基频混合在电平方律非线性中.三阶项可表示如下

:
其中, 是结温,TF是比, 是从非线性源到集电极的跨导倒数. 需注意到,模式是一直不变的:低频温度变化调制电路元件值,使其与基频音调相混合.结温的计算是基于耗散功率
仅仅包络音调,这将产生一阶和二阶音调,
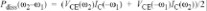
被精选下来,并与热阻相乘以得到结温的变化.耗散源是一直不变的,但是如果不同的电路元件需要不同的温度,热网络可以用Z矩阵来模拟. 级联的二阶非线性IM3成分同样很复杂,在此不详述,见附件C,并且它们的数字值在第4.4.2和4.5节中用矢量图表示.需注意,包含由温度决定的电荷项
不能被计算,除非找到一个测量它的值的方法.
由上文和附录C可见,对一个简单的CE放大器的符号的Volterra分析变得十分棘手,许多复杂的拓扑很难对其解析地进行分析.然而, Volterra计算可用数字计算来进行. Nlsim软件[24, 29]能够用数字计算非线性电压元件,并且能对更复杂的拓扑进行分析.与完整的解析方法相比, Nlsim对失真的描述稍微粗略,且不分开级联的二次非线性,但是它能简单地显示每一个非线性的立方项以及向上,向下转换包络和二次谐波项.不论如何,二阶相量可以被划分为矢量的和,从而看出哪一个是主要的二阶成分.
4.4 BJT CE放大器中的IM3
在这里,我们研究两种不同案例下的IM3失真:首先,使用一个将非线性输入和I-V曲线级联起来的简单模型,然后用全电路,包括反馈效应,采用前面章节所描述的全分析.
4.4.1 BJT作为两个非线性方框的级联
如前文所讲,BJT放大器的失真成分十分复杂,因此,需要首先做些简化来找出失真成分的基本特性.之后将会给出一个完整的分析,

但是暂时忽略发射极阻抗
反馈电容和
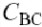
产生的反馈影响,并简单地认为集电极电流是一维的,仅受基极电压的作用.图4.10给出了简单的电路,由于所有的反馈效应被忽略,BJT的集电极电流可以被简单地认为是两个非线性方框的级联,如图3.5所示.第一个方框包含输入非线性Cpi和gpi,第二个方框包含一维跨导的非线性.
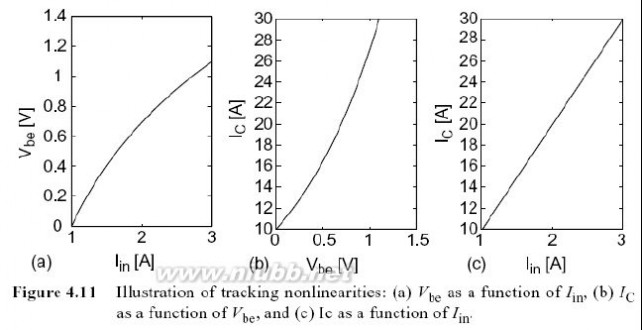
我们知道,当采用电压激励或电流激励时,CE BJT放大器的线性特性是不同的.在理想化的情况下,零的电压激励使得输入非线性可以忽略不计,这是因为输入和基极到射极电压是相等垢,并且电压源使得所有失真电流短路.于是图4.10中唯一有效的非线性成分是跨导.如果采用电流源激励,情况就会改变.图4.11(a)指出基极到射极电压是输入电流的函数,图4.11(b)描述了集电极电流,它是基极到射极电压的函数.图4.11(a)可以看成是一个对数函数,图4.11(b)是一个指数函数,作为它们的级联,集电极电流是输入电流的函数,是一条标准的直线,如图4.11(c)所示.因此,当晶体管受电流驱动时,被电压驱动的BJT的强大的指数非线性消失了.同样,在实际中,激励的类型可以通过适当调整ZIN值来改变: ZIN的值越高,CE BJT就越表现为由电流驱动.

图4.10 简化的BJT模型,忽略了反馈的影响
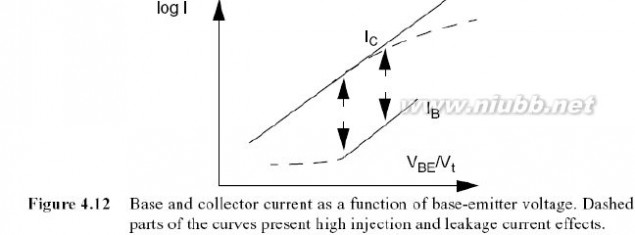
图4.11中,两个相反的非线性相互抵消.同样的现象也在图4.12Gummel图中被证实,其中,集电极和基极电流是的函数.由于采用了一个对数的Y轴,这些完全地指数非线性表现为直线的形式.可以观察到,线之间的距离(例如电流增益)是常数且不依赖于的值,这表明,非线性的形状是相似的.
这种两个非线性相互抵消的现象通常称为跟踪非线性,结果导致非线性元件线性工作.然而,在实际中,非性线特性不能完全地进行跟踪,结果是一些非线性经常存在.例如,图4.12中线的虚线部分表示了实际情况:跨导在高值时不再是纯指
值数的,这是由于在基极有一个高注入电平,因而减小了电流增益.同样,在低
处,一些基极泄漏电流经常存在

.
图4.11 跟踪非线性的描述

(a) 是 的函数(b) 是

的函数
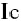
(c) 是的函数
接下来,将分析图4.10所示的电路的交流特性.第一个方框的非线性是由gpi 和 Cpi引起的, gpi被认为是完全的指数的, Cpi也认为是指数的,从前向传输时间( )和跨导gm来计算

:
后面的方框描述了非线性跨导,它的非线性可以用(4.1)来计算.如果我们忽略早期效应并仅使用一维的集电极电流,就可以得到如表4.2所示的非线性系数.表中第二
列对应于严格的指数低注入的情况,第四列出示了一种高注入的情况,在这种情况下, 跨导的非线性减小,见图4.12中虚线部分

.
图4.12 基极和集电极电流,作为基极射极间电压的函数.曲线的虚线部分表明高注入和漏电流效应
表4.2 跨导的非线性系数

在第三章中已经讨论过级联的非线性失真成分,并在图3.6中加以描述.级联的IM3L集电极电流为
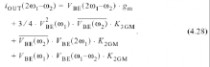
:
IM3L由4项组成,前两个分别由第一第二个方框内部直接产生.后两个涉及到二阶交感,通过方框间的包络和二次谐波频率产生.在第一个方框中,失真是由输入阻抗的二阶非线性产生, (4.28)中基极的频谱成分可用表2.6计算.
首先研究图4.10电路中基本的作用.非线性系数用等式(4.1)和(4.27)计算,基于BFG11射频功率BJT[32]的GP模型SPICE参数.在中心频率1.8GHz和音频间距1MHz处计算IM3电平.如果与内部基极电阻相比,输入阻抗的值较高,输入将表现为一个电流源,并且输入输出非线性将会部分地进行互相抵消.
在整个合理的值上,在基波的
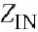
被扫描,用以检查电压/电流激励的作用.BJT的输入是变化的匹配,这说明输入电抗已被确定,所以基极电抗关断
.在谐波和包络处的值被设置为无限大,这说明
在这些频率处的基极阻抗仅由内部基极到射极阻抗组成.图4.13中显示出在集电极电流两个值处的IM3失真成分,它是基波的函数. 图4.13中同样显示出IM3的不对称性(例如,低边带和高边带之间的矢量误差)
在低注入的情况下,通过将
加值增加到20 到30 ohms来提高IM3值.继续增值,并不再减小IM3,因为输入非线性和输出非线性之间的不完整跟踪,将IM3
,情况有所
,在一些相关的低值处,仍
的优点是在最适宜的限制在–57 dBc,如图4.13所示.在高注入的情况下不同:尽管在此情况下,

线性并不十分依赖于高值的可以达到线性的重大提升.与拐点电流IKF相比,

较高的处,线性得到较好提高.
当基波的虚部开始从共轭匹配的情况下增加时,线性开始恶化,即使它可能稍微地减小,IM3边带间的矢量差(例如不对称性)可能减小.图4.13中较低的曲线表明了低IM3音调和高IM3音调之间的不对称性.通过使输入匹配稍微是感应的,在IM3边带对称性上可以有多于10 dB的提高. [33]中也有相似的观察,其中研究了输入阻抗对相位失真的影响.对称性的提高对于包括线性在内的应用而言,是一个非常重大的提高.

图4.13 集电极电流IM3边带的幅度,它是基波输入阻抗的函数
由于大量的输出三阶失真是通过级联的二阶非线性产生的,所以对带外的仔细优化能提高线性.三阶项不会被滤波影响太多,这是因为它们的功率与基波信号交迭,但是二阶信号的功率位于基波较远的地方,且可以通过使用滤波来达到最佳可能的线性[27, 34-36]. 同样,例如增益和效率的基波匹配也有许多要求,因此基波阻抗的选择,不能只基于线性特性.然而,带外匹配仅对增益和效率产生次要的影响,因此,有时可主要依靠线性来调谐带外匹配.
现在,我们来研究二阶信号成分的作用.当在包络被扫描时,基波周围的阻
and )引抗保持常量.在图4.14(a)中,较高的八段向量表示由输入非线性(起的输出IM3产物,而低三段向量的前两个向量表明输出三阶IM3产物是由二阶输入输出非线性引起的.这两个中的第一个是通过基极的包络产生,另一个是通过二次谐波产生.低三段向量中的第三个表示跨导的立方非线性.有趣地注意到:由二次非线性引起的IM3向量部分,与由立方非线性引起的向量部分相反.这表明,非线性间的互相跟踪有两种方法:第一种是通过前面讲述的输入输出跟踪法,这种方法表明,基极
的失真电压波形抵消了由非线性跨导引起的失真;第二种方法是通过二阶和三阶非线性间的抵消.由于使用了大量的转移函数,后面的这种方法在本书中较难用等式来表示.然而,如果我们忽略Cpi,并根据(4.29)中的电路元件和系数写下三次谐波电流的表达式,可以清楚地看到,二阶和三阶系数的符号是相反的.

图4.14 (a)部分跟踪非线性的表示(b)向量结果. 两个输出IM3信号由于11部分组
成…..(e表示包络,h表示二次谐波
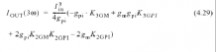
)
图4.14(b)描述了包络处四个阻抗值的IM3结果(由部分跟踪非线性引起).如
果阻抗幅度高,输出IM3信号将不被其相位所影响,但是如果阻抗幅度相对较小,至多比基频处的
处的高10,其相位将会起着重要的作用.为什么仅在较小时,包络对IM3有影响的原因十分简单:

如果高,基极结点的总阻抗受晶体管内阻抗的控制,但是当小时,它却影响整个结点阻抗.
的方法来减小总体失真.从上面可以看出,这并不
值,或者提高IM3边带间的平衡来减小总体
(ω2–ω1)又混合到不同边
在高IM3边带和通常建议用最小化低频常用;然而,可以用一个较小的假定失真.既然失真电流与 (ω2–ω1)

相乘,而带中,

且它们的阻抗相位相反
低IM3边带间,当纠正相位错误时就会得到一个小的反应基带偏置阻抗.
4.4.2 详细的BJT分析
现在,我们使用完整的Volterra模型来研究单个失真结构的作用.在这种情况下,模型的非线性系数是通过实际测量得到,其采用的步骤在第五章中将会有详细的解释.在本节中,我们研究CE BJT放大器线性上不同频率处的偏置点和优化终端阻抗的作用.
大家都知道,CE放大器的最佳阻抗随偏置情况而变化.如果我们用实验的方法来检查所有可能的基波输入和负载阻抗在不同偏压点的结合,并且也考虑包络和谐波阻抗(对线性影响很大),那么,单个CE级的优化都会变成一项十分冗长的工作. Volterra模型(假设它足够精确) 通过在不同偏置情况下设计最佳输入和负载阻抗,被用来优化CE放大器的线性.
一个基于BFG11晶体管的放大器[32]被建造,并且在基频1.8 GHz处的输入阻抗被调谐成共轭匹配以用于最大功率转换.负载阻抗已确定,因此输出电抗的虚部和匹配网络在外部相互抵消, 且的实部由期望的I-V特性所决定.可以通过降低值来提升线性,这是因为集电极的电压摆动减少了,但不幸的是,同时效率也有所减小.所以在线性和效率之间,选择20 ohms作为的平衡值.零频率附近的负载阻抗
很小,这样可以从电流源提供直流功率给集电极且损耗最小.放大器在二次谐波处的输入和负载阻抗分别是0.1+j76和31+j17,在包络频率为2MHz时, 输入和负载阻抗分别是13–j0.2 和0.2–j1.4.这些数据都是由实际的放大器测量得来.
首先扫描基极和集电极偏置电压,并且监测线性以便找出偏置的一些基本特性.为了使仿真之间有可比性,输入电压摆动和负载阻抗仅被稍微调谐以保证在变化的偏置情况下,输出电压和电流摆动是常量.选择输出电压摆动为1.5 Vpp,这意味着在集电极电源附近的IM3值低于1V是不精确的.图4.15(a)描述了计算的IM3L曲线和测量的IM3L点,可以看出,它们相互之间有着很好的相关性.
在偏置电流为75 mA时,线性最大,当偏置电流减小时,线性开始恶化.当偏置电流降低到40 mA时,IM3边带增加约10 dB.集电极偏置电压同样也影响线性,因此在电压值为3.5V时,线性最大.图4.15(a)中没有显示出超过4V的集电极电压,因为高的集电极电压仅仅减小了效率并没有更远地提高线性.电流较低时,线性彻底不依赖于集电极电压,但在高电流值时,集电极电压却起着非常重要的作用.这是显而易见的,因为在低电流值时,由gpi, Cpi和gm

引起的非线性比由 和 交叉项引起的非线性要强.此外,在高电流值时,非gpi, Cpi和gm引起的非线性较弱,这是因为跨导的原因,例如,由于高注入作用产生的电流线性化.同时,既然
值的情况下十分强大,对于总体失真来讲, 和其非线性在高集电极电流起着更主要的作用.
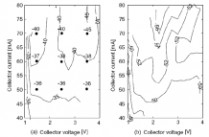
图4.15 (a)计算的和测量的(网点)IM3L(b)测量的非对称IM3L-IM3H
IM3H边带的轮廓点图与IM3L的十分相似,如图4.15(a)所示.边带间的向量差用dBc描绘出来,以便与基波信号作对比, 如图4.15(b)所示.需要重点强调,此图形不仅取决于偏置值和匹配阻抗,它也取决于调制频率.如果采用预失真的线性化方法,边带间的非对称性是一个重要的品质因数,如第三章所讨论.
在前面的例子中,选择基波输入和负载阻抗的值,用来达到需要的功率和有着合理效率的增益特性.然而,为了达到可能的最佳优化,必须对带外包络和谐波终端进行优化.通过调谐带外终端来提高线性的一个最常用的方法是,使得二次谐波处的负载阻抗最小化.既然部分的IM3成分是由二次谐波电压引起的,在此频率处的阻抗也影响IM3.而这些是否有助于线性的提高取决于非线性系数和其它的阻抗.为了检查二次谐波匹配的效果,在那点频率上的负载阻抗的实部被减小到6 ohms.比较的结果见图4.16,它指出了在所有偏置情况下从1 dB 到 5 dB的改进.这些计算指出,为了达到最佳性能,带外阻抗需要进行优化.这里仅证明了二次谐波负载阻抗的影响,但是其它的带外影响同样重要.经选择的最优带外终端阻抗可以将线性提高几分贝,而不减小基波的功率和效率性能.
如第三章所述,IM3边带间的不对称性受包络阻抗的严重影响.在多载波发射机中,信号的带宽可能很宽,例如,在直流和20 MHz间很难设计常量阻抗.输入和负载包络阻抗通常不是常量,由于IM3边带是这些阻抗的函数,它们随调制频率而变化,从而引起记忆效应.
通过扫描一个双音信号的音频间距(集电极电压是3V,基极偏置电压是740 mV),我们来研究记忆效应.用Volterra计算的IM3L的相位如图4.17所示,它是音频间距的函数,并且符合三种不同类型的记忆效应:低频处的热记忆效应,共振型的记忆效应以及高频记忆效应,后两者皆由偏置电路引起.
在1 MHz处的谐振由一个谐振集电极阻抗引起.使用Gummel-Poon (GP)模型不能观察到谐波平衡仿真,因为其过分简单的输出阻抗掩饰了集电极谐振的效果.在高调制频率处的平滑相位偏移是由包络频率处的输入阻抗引起的,仍然是使用GP模型进行模拟.由于动态的自我加热效应在基本的GP模型中不被执行,就不能预测由热效应引起的低频记忆效应.
Volterra模拟适合所测量的结果,如图4.17所示,第六章会有更详细的说明.因此, Volterra模型似乎是一个更好的工具,用来确认功率放大器的记忆效应.

图4.16 在二次谐波不同负载阻抗处计算的IM3L(细线是35欧,粗线是6欧) 接下来,我们研究IM3相图的微细结构.此信息可以用来进行设计优化,此处所画的IM3是作为十个组成项的矢量和,以便用来研究为什么IM3L的相位取决于调制频率.我们选择三个频率点来画矢量图,分别是100 kHz, 1 MHz,和1.1 MHz,并研究1 MHz处的谐振和热记忆效应.
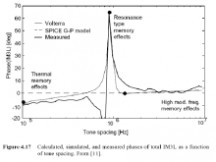
图4.17 总IM3L计算的,模拟的,测量的相位,相位是音频间距的函数 我们首先来看看,在音频间距为1.1 MHz的谐振上发生了什么.在图4.18(a)描述了IM3L相量,它是实轴虚轴上一系列相量的和,从图中项端的中心开始.此相量由49个纯电气项组成,前面的7个由立方非线性引起,后面的42个由级联的二阶非线性通过包络和二次谐波频率引起.电热项几乎是零,因为1.1 MHz的差频频率已经位于热滤波器的衰减带中.
前面的7个点(1-7)是立方失真机制,其中 (6)最大.接下来的21个点 (8-28)是由包络频率得到的向上转换的IM3成分,最后的21个点(29-49)是由二次谐波得到的向下转换的IM3成分.这是由于一对对之间部分地进行相互抵消:三阶非线性和部分的抵消,同样的, (29,其中二
(37,由混合在
(45,二次谐波由混合在次谐波由返回到输入进行再混合的gm产生)和中的gm产生二次谐波),

或者
中的gm产生)和生

) (48,
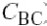
二次谐波由被放大并混合在中的Cpi产
图
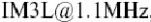
4.18 (a)
(b) 和的向量表示

之间的向量差
成比例的失真在基本处被转换为电压, 怎样可以提高线性呢?与

并且它的组成成分(6)

可以通过调整的相位,朝着原点旋转;可以通过降低二阶谐波阻抗来减小整个29-49网孔的大小.另一方面,二次谐波处的基极阻抗可能会增加5%到10%,从而使得总和更加接近于零.
从记忆效应的观点来看,当音频间距减小到1 MHz时,研究会发生什么情况是十分有用的,刚好会遇上ZL内的谐振.这在图4.18(b)中被论证,它表明, IM3L@1.1MHz和IM3L@1.0MHz的差是一个相似的相量和.首先,由于基波单调的相位不变,立方非线性(1)-(7)表现相同. 二次谐波的混合产物(29-49)同样是相等的,这表示二次谐波的终端阻抗是平滑的.所有这些引起IM3谐振的决定性原因是由于级联的二次非线性,它向上转换包络频率—大的项包括
的输出包络), (24,

混合到
(26,

被放大并混合到
基带频率响应.
接下来,我们研究在音频间距为100 kHz时,由电行为和热行为之间交感作用产生的记忆效应.图4.19中描述了用向量的第一段表示的纯粹的电IM3向量,在如此低的频率下,它们几乎都是一样的.电热的三十段向量用逐项列出的方法显示,且可以看出电热失真是由K3GMT, K2GMT, K3CPIT和K2CPIT项控制.
然而,需要注意IM3L和IM3H间的大的相位差.这仍是因为基带效应,包括热反馈,与相反的相位混合到较低的和较高的IM3边带中.除了相位的不对称性,热反馈同样引起了IM3L和IM3H之间幅度不对称,这是因为原点和终点78之间的距离对于IM3L和IM3H是不同的. (14,混合到里的输出包络), 的中的输入包络,这些都包括了
四 : 第四章Volterra模型
第四章 Volterra模型
在本章中,我们首先回顾最常用的非线性建模方法.第4.1.2节讨论多项式Volterra模型建模方法的特性,第4.2节详细解说记录下来的完全电非线性和电热非线性,以及建模非线性级数展开中所用的项.4.3节描述了如何应用Volterra分析方法计算一个普通发射放大器的失真,并且作为第一个研究案例,第4.4介绍了在一个BJT CE放大器中,影响IM3失真的所有项的分析.同样的分析(对一个MESFET放大器)在第4.5节中介绍.
4.1非线性建模
为了能够分析功放的非线性行为,我们需要为实际的非线性电路,无源匹配以及偏置元件建立精确的模型.但此模型的获取又有一定难度.众所周知,N阶失真的数量与I-V和Q-V波形的N阶导数成比例(参照[1-3]).因此,为了达到精确的失真模拟,对有源元件的I-V和 Q-V波必须建模,因此不仅是直流值,高阶导数同样是正确且连续的.(为了便于参考,在早期的仿真模型中,第一阶导数可以不连续).此外,电容是很容易建模的,因此电荷没有存储,这将导致完全容性结点的非物理整流和自偏压.因此,特别是如果电容值同时取决于两个终端电压,将电容模拟等效于电荷平衡是十分重要的[5].
由于无源元件在高频具有分布特性,很难在射频频率上对其建模.有损耗的传输线难以在时域上进行建模,一般而言,无源元件的建模在频域上更加精确.尽管如此,有些无源元件的频域仿真模型在高次谐波时也可能是不准确的,例如传输线宽上的阶跃变化,在电路分析中,可以采用测试电路的标准终端阻抗值来进行分析. 简而言之,为了得到精确的失真模拟,从模拟模型中需要:
1. 对N阶失真模拟来说, I-V 和Q-V波形的N阶导数必须足够精确.
2. 结点阻抗的频率响应对于最高相关谐波,必须是正确的.同时,在基带频率,偏置阻抗和热阻抗的正确模型也是十分需要的.
3. 如果可以得到主要失真源的组成信息,将十分有用.
4.1.1非线性仿真模型
volterra 第四章Volterra模型
通常来说,功放和发射机设计师使用两种非线性模型:一种是用于系统仿真的行为黑盒子模型,另一种是用于电路仿真的器件模型.根据建模方法的不同,可以对这两类模型进行更深层分割:可以是解析的,基于一些预先确定的和物理学的用参数表示的模型函数,或者完全根据实验的,将测量数据列表并以内插值替换的,或者用简单的曲线或物理意义不清楚的多项式表示的模型.在表4.1中有所介绍.
表4.1 功率放大器的非线性模型

行为基带模型广泛用于模拟和优化整个发射机和收发器,并且增加了新的功能,例如模拟记忆效应,在[6]中介绍.然而,行为模型描述的或者是一个已经存在的放大器,或者行为模型源自到目前为止不存在的放大器规范说明,但是在设计一个新的功率放大器中,行为模型的使用遭到限制.
这里简明地介绍了最常用的行为模型的特性,仅用于参考.简单的静态的AM-AM 和 AM-PM波形不能够模拟记忆效应,但是基于调制频率的AM-AM和AM-PM波形的模型已经被开发出来.如图4.1所示,在Saleh模型中, AM-AM和AM-PM非线性模块的输入和输出端都增加了线性滤波器.在Blum 和Jeruchim(在[7]中描述)模型中,用快速傅立叶算法及足够的抽样来找到用于修改AM-AM表的瞬时调制频率.有一种Volterra型的行为模型被称作Volterra输入输出图(VIOMAP).它是普通S参数的非线性的概念性扩展,包括谐波响应,并且被成功应用于单音负载下拉仿真中[9,10].
volterra 第四章Volterra模型
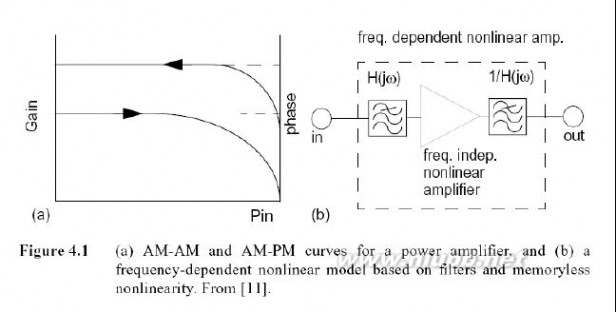
图4.1 (a)功率放大器的AM-AM和AM-PM波形
(b)基于滤波器和无记忆非线性的由频率决定的非线性模型.
器件模型描述了半导体设备的动作,以及无源和分布式元件的合适模型,可以建立并优化功放的模型
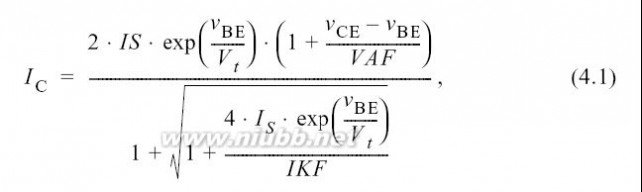
.
早期的半导体模型是解析的,所采用的等式首先来源于半导体物理学,然后将其简化以减少仿真时间.这些基于等式的模型的一个基本问题是,所选用的函数和控制参数固定了I-V 和Q-V特性的可能形状,并且可能没有足够的自由度来模拟例如IC-VCE曲率.例如,在基本的Gummel- Poon (GP) BJT SPICE模型中,集电极电流的简化形式如下:
volterra 第四章Volterra模型

其中, 基本的指数仅可被三个控制参数修改: IS依比例决定电流, VAF (所谓的早期电压[12], 如图4.2所示)构成输出电导的一个极其简化的模型, IKF (所谓的拐点电流)降低高电流时的增益[13, 14].这个简单的等式涵盖了整个I-V平面,同时固定了导数dnIC/dVn,因而固定了非线性行为. SPICE GP模型可以适当地用于模拟基带信号[15],但是特别是对于过分简单化和固有性线的输出阻抗模型, 不能用SPICE GP模型进行精确的失真仿真,这将在本书后面说明.
更好的物理模型已经被开发出来,比如BJT的Mextram和VBIC ,以及用于LDMOS的摩托罗拉MET模型,这都是久经考验的模型.与早期的SPICE模型其比,这些模型的性能大大地提高了.后者对于找到正确的直流偏置十分重要,这是因为自我加热使得I-V波形产生一个大的差值.假如热模型有足够的时间常量来模拟缓慢加热包(主要影响直流偏置和芯片表面的微秒范围热记忆),后面的模型也可用于模拟热记忆效应

.
图4.2 在BJT中使用早期电压VAF模拟输出阻抗
volterra 第四章Volterra模型
模型的额外自由度增加了其复杂性以及控制参数的数量.在一个极限中,MOS BSIM模型有数十个参数来单独控制比例特性.因此,模型的复杂性趋于失控,并且其配置愈加复杂,对错误愈加敏感.
另一种设备建模的方法是放弃等式,而采用列表的测试数据或者完全根据实际以验的函数来代替.现在,任何形式的I-V和Q-V特性的模型可以被建立,这是通过Root模型得到的方法,称作” 设备最了解”模型[5].在内插列表数据时,存在一些技术问题,这是因为内插的多项式容易使数据点之间产生振荡,因此派生出高阶非物理波动.然而,由于预定函数不需要压力,列表模型使用灵活.
Volterra模型是一种经验模型,它不依赖于半导体物理学.其非线性描述为多项式,系数可以通过对I-V和Q-V函数微分得到,也可通过将多项式直接填入测量数据表里得到.在此我们使用的是后者,在接下来的章节中,我们将会更深层次地对Volterra模型的特性进行研究.
4.1.2 Volterra模型的特性
多项式模型并不自动地对模拟快速响应,相反,它可能严重地会聚在高于原始设置范围的信号电平上.然而,多项式模型允许使用高效的Volterra分析程序.
然而,采用Volterra模拟方法的主要动机并不是看中了其速度优势,而是它能提供一个极好的分析工具来进行分析.主要的失真机制可以用与在普通交流噪声分析中采用的相同的方法来进行分析,由于非线性分析,多重的混合机制同样可被识别,例如可以帮助谐波终端阻抗的设计等.因此, Volterra分析是少数可以帮助理解记忆效应和帮助设计优化的方法之一.
尽管如此,仍需承认多项式模型存在一些缺点.首先,多项式模型要遭受在适宜的带宽范围外,其响应接近无穷大这一事实.传统的非线性建模函数与此正好相反,它在整个偏置范围内平滑,有限的表现是我们设计的特性,因为它帮助使信号收敛,并且信号摆动不必要进行推理的了解.因此, Volterra分析并不是一个非常普通的工具.由于速度原因, Volterra分析被用于快速失真分析和模拟器中的低噪放型小信号电路(例如Voltaire XL [22] 和SPICE的早期版本)中,或者甚至做为独立的模拟器使用[23]. 然而,为了功放能被成功地进行分析,可靠的早期信息仍是必需的.
volterra 第四章Volterra模型
第二, 预先得需要实际的大信号直流偏置电压.大信号动作经常会引起直流工作点的移位,它同时影响增益和非线性的数量.此信号感应引起的直流移位会减缓谐波平衡模拟中收敛的速度,并且在非反复Volterra计算程序中,只能对它进行估计,而非完全地预测.为了克服这点,我们需要检查直流移位是不是很大,或者在实际的大信号工作点使得多项式模型合适.
第三,在多项式函数的装配中,需要知道输入和输出电压摆动的范围.多项式模型的实际功率是除开失真成分的其它部分.适宜的范围越大,低阶多项式的精确度越小.因此,沿着最大信号振幅安装是合适的,为确保多项式模型的精度,不能太超过此范围,并且由于多项式响应可能在合适的范围外是完全非物理的,也不能超过一个较小的范围.在这种情况下,就需要对输入输出轨道有较好地评估.总之, Volterra分板并不是一种简单使用的独立的仿真方法,但当它用在与其它仿真方法(例如谐波平衡)并联使用时,此方法提供了更多调试功能.
在本书中,研究的案例仅限于单级晶体管放大器,并且对Volterra分析半解析地计算(象征性地来源于每一个失真源到所有结点电压的转移函数). 象征性的分析并不是必需的,它限制了对CE或CS放大器固定的结构以及双音测试信号的分析.而Volterra分析却能达到,通过在(用标准修改结分析矩阵以及非线性电流源表示的)任何电路上运用通常非线性交流分析方法.
4.2非线性I-V和Q-V特性
大多数的晶体管模型是以Π模型或T模型为基础.这里使用的是Π模型,本节中描述了用BJT,异质结BJT(HBT)和场效应管(FET)的Π模型表示的典型传导(I-V)和电容(Q-V)的非线性特性.在这里将BJT作为一个案例,但同样的模型也可用于FET晶体管,只是多项式系数设置不同.
前面已经讲过, Volterra模型是以I-V和Q-V曲线的多项式建模为基础.测量这些曲线也许会有些困难,详见第五章.这样的电荷不能直接进行测量,我们必须依靠交流测量的电容以及对所得电容值得到的电荷等式求积分.用类似的方法,I-V曲线可以通过由S参数测量得到的
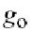
一个更安全的出发点. 和值进行大部分重造,但是实际的I-V曲线是
volterra 第四章Volterra模型
这里介绍的模型是电热模型,这意味着其结温是一自由变量.然而,直流温度上升包含在偏置点中,并且只考虑由动态自我加热引起的温度变化.由于功耗是电压和电流的产物,我们认为结温中的交流成分已经是一个二阶现象.因此,一个三阶的模型仅仅包括温度的一次方,这意味着电容元件的温度依靠性被认为是线性的.
4.2.1 特性
在大多数被报导的BJT/HBT Volterra级数分析中,集电极电流被认为只是基极电压的函数[25-27],此考虑方法抓住了主要指数的输入输出非线性但是认为输出电导是常数.在MESFET Volterra级数分析中,漏电压的效应通常用
实现, (参照[28]),但即使如此,也难以捕捉所有的非线性特性.
在(4.1)式中,等式
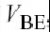
是
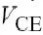
,和结温T的一个三维简单函数,就像的一个多项式来
.通过扩展大信号I-V函数
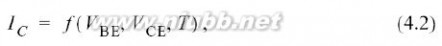
到一个三输入的泰勒级数(在直流工作点
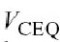
,和周围),很容易得到一个多项式模型.因此,交流电流的电热三阶级数展开可以写作
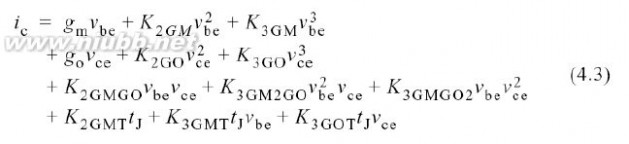
:
其中,
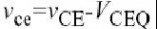
元素xxx的i阶非线性系数.(
第一行只受影响,
第二行只受,, 并且Kixxx是).由等式可见,可以用来标志影响(例如非线性输出电导).尽管如此,第三
volterra 第四章Volterra模型
行又列出了的温度变化. 和的向量积.最后,第四行列出了与两个终端电压混合在一起图4.3中证明了电非线性的影响,其中,绘制了在三个基极电压处的集电极电流,它是三个不同基极电压处集电极电压的函数.如果除外的所有系数都是零,我们可以得到如图4.3(a) 所示的三条等间距的水平线.由于线精确地保持水平,输出电导为零,且集电极电压不影响电流数量.此外,由于线之间等间距,跨导是线性的.然而,如果导是非线性的. 或偏离了零,在I-V平面的线距离将会变得不等,这表明跨
volterra 第四章Volterra模型
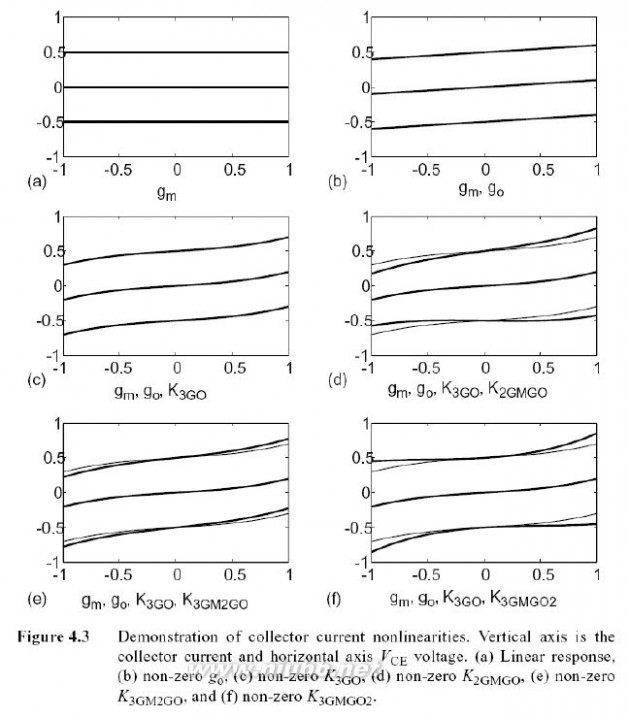
图4.3 证明集电级电流非线性.垂直的轴是集电极电流,水平轴是(a)线性响应(b)非零 (c)非零 (d) 非零
非零 (e) 非零电压. (f) 图4.3(b)证明了的影响,

仅仅存在和.与图4.3(a)相比,图4.3(b)中
volterra 第四章Volterra模型
的线有一个非零的斜率,它与
成比例且不依赖与.
图4.3(b)仍是完全线性的, 图4.3(c)证实了输出电导的非线性,其电流的斜率随而变化.在这种情况下,

仅有一个非零值,
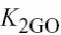
和可被用于模拟输出电导的曲线效应,例如饱和和击穿.
图4.3(d-f)分别图解说明了
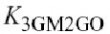
,和的截项,它模拟了基极和集电极非线性物性的交互作用.为了帮助比较,图4.3(d-f)中的稍细线是临摹图(c)的(
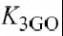
和都有非零值).
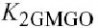
(对应于
项)在图4.3(d)中是非零的,这是由于其线的斜率变化不仅仅受图4.3(c)中集电极电压的作用,也受基极电压的作用.这对于图4.2所示的模拟早期效应是十分必需的.相似的推理也可应用于
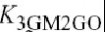
确定输出电导的形状,分别是
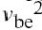
和和的函数. ,如图4.3(e, f)所示,
图4.4对不同建模方法的I-V曲线做了更多的比较.如果集电极电流被模拟为基极电压和线性的一维函数,就产生了一条直的I-V线,如图4.4中细虚线所示.用SPICE Gummel-Poon模型模拟的I-V曲线同样也是直的细的线,但是其斜率和输出电导随集电极电流变化,如图4.2所示.实际上,由于准饱和和截止影响,在大信号或半大信号的情况下,BJT的I-V曲线决不是直线.曲率可以通过使用和的一维多项式模拟,如图4.4中粗实线所示.然而,初步的现象(例如早期效应)在没有引起斜率决定于的值截项时不能被模拟.如图中粗虚线所示,并对应于
(4.3)的完全级数展开.饱和和截止的开关同样取决于基极电压,这使得截项的使用强制地避免了I-V平面角落处的重大误差,如图4.4所示.
volterra 第四章Volterra模型
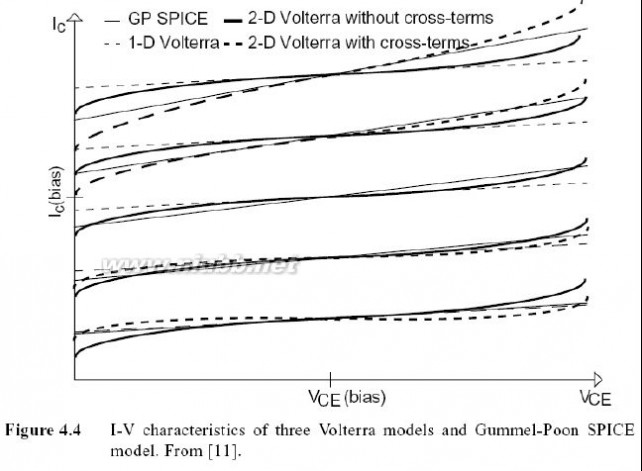
图4.4 三个Volterra模型和Gummel-Poon SPICE模型的I-V特性
最后讨论了集电极电流的电热效应,如(4.3)中最后三项所示.在图4.5(a, b)中,描述了一个二次项
不能由小信号参数,它模拟了电流中由温度决定的移位.值得注意的是, 和得到,相反的,需要实际的电流测量. 是一个包含温度和集电极电压影响的三次项,如图4.5(c)所示.它在本质上模拟了温度对输出电导的依靠性.同样的,如图4.5(d)所示,

度和基极电压的结合效应.由于曲线的斜率反应了跨导,
度影响的跨导的一个变化. 模拟了温可被认为是受温
volterra 第四章Volterra模型

图4.5 电热非线性系数的影响. 非零
轴.(c)非零 影响(d)非零影响

在(a) 轴(b)
特性是FET型晶体管中唯一重要的传导性非线性.在BJT中,存在另外
的两个非线性:由指数
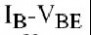
引起的非线性和非线性.电导的影响通常更重大,并且也容易模拟.理论上, 等式可以粗略地用电流增益β除,但可用一些方式简化.由于基极电流并不是强烈地依赖于集电极电压,我们可以用一个仅由和决定的两维模型
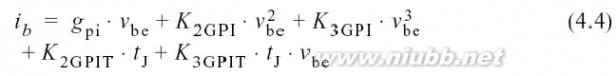
:
这里,系数与之前有着相似的含义.线性项通过进行模拟,
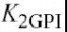
和
volterra 第四章Volterra模型
模拟其指数曲率.此外
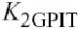
, 可以看成线性
本征基极电阻模拟了由自我加热产生的移位, 项的温度依靠. 较难模拟.它是内部基极点和外在基极点之间的串联电阻,
值.因此,它可以模拟为一个由
和结温控制的三维电
和它的值取决于基极区的电流拥挤,也取决于内部电阻器电压
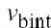
(导.所有的),内部基极电压
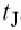
K项(k=1,2,...)都是零,

但是电流拥挤效应是用间的截项模拟的,如(4.5)所示.不论如何,
一个线性电导
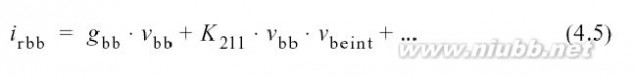
. 通常较小,且在下面例子中被模拟为
4.2.3电容模型
如前面解释,将电容建模成多项式电荷,然后将其关于时间进行区分以得到位移电流.电荷可能并且经常是由多于一个的端口电压所控制,这使得我们必须使用一个类似于(4.3)的多维多项式.电荷同样可以模拟为一个电容,在这种情况下,电荷不出现在控制结点之间,而出现在一些其它的结点间.在下面的例子中,只假定了一个控制电压,式(4.6)描述了基极到发射极的电荷,它是基极到发射极的电压以及温度的函数
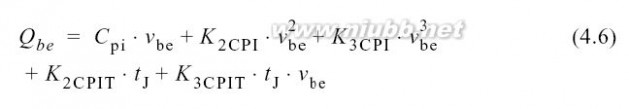
.
从这个等式中,可以轻松地得到对应测量电荷Cpi和非线性电流源
需将电荷等式(4.6)分别关于和时间进行区分即可. .只
volterra 第四章Volterra模型
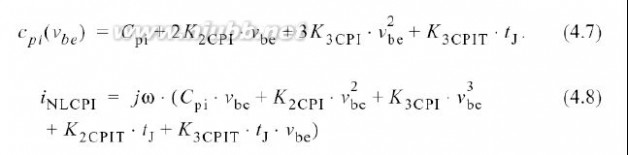
在(4.8)式中, ω仅是失真音调的频率;因此,电容并不会引起直流失真电流但是在谐波频率处失真最严重.等式(4.7)指出由温度决定的电荷项K2CPIT不能来源于电荷测量;尽管如此,一个时变的结温可能引起一个与它成比例的电流.另外, (4.6)式中的第一项Cpi描述了小信号电容, K2CPI和K3CPI定义了它的有关电的非线性. K3CPIT描述了是控制电压和结温函数的电荷,由于C = dQ/dv, K3CPIT的作用可以看成是电荷值的温度决定性.
如(4.6)所示,一个线性的C-V趋势K2CPI引起了二次电荷非线性.同样的,与v2 (K3CPI)成比例的电荷引起立方的非线性.不同类型的电容有着不同的特性,如图
4.6(a)所示.如 (4.27)所示,基极-射极电容Cpi是指数的,因此它是高度的非线性的.BJT和FET中有偏的P-N结或肖特基结仅是稍微的非线性,它们可以通过增加反偏压进行更深一层的线性化. MOSFET型晶体管有着特殊的栅电容,例如, CGS在门限电压的周围dip.如果MOSFET动作接近于关断,此dip会引起大量的二阶非线性.
volterra 第四章Volterra模型
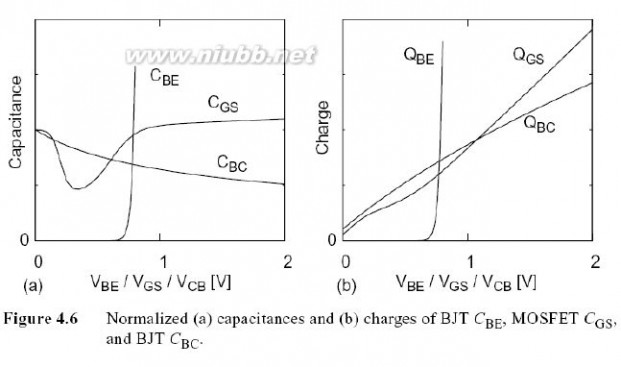
图4.6 (a)归一化的电容(b) 和的电荷
4.3共射极BJT/HBT放大器模型
现在我们使用直接的方法来计算一个共射极BJT/HBT放大器的IM3成分,使用第
2.5.2节所列出的步骤.这样进行分析:首先为电路建立一个模型,通过一个线性的交流分析建立基本的幅度.然后,通过使用第4.3.2节所示的步骤计算二阶电流电压以及三阶电流电压.
4.3.1线性分析
图4.7所示的是一个共射极BJT放大器,它包括输入阻抗ZIN(混合匹配网络和偏置电路),基极-射极电导gpi和电容Cpi,反馈电容CBC,输出电容CCE,输出电导导跨,负载阻抗ZL以及发射极阻抗ZE.输入和负载阻抗不仅包含匹配网络的阻抗,也包括偏置网络和包寄生的阻抗, ZIN由前级的输出阻抗和本征基极电阻rbb组成,如图4.7所示.
volterra 第四章Volterra模型
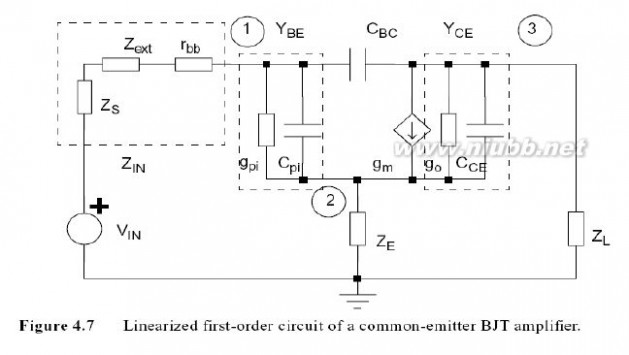
图4.7 共射极BJT放大器线性化一阶电路
为减少等式的数量,输入电压源可以用诺顿等效源来代替

且用下列简化符号

通过替换图4.7中所有阻抗并在结点1至3应用基尔霍夫电流定律,可以得到如下矩阵等式.
volterra 第四章Volterra模型

通过使用Cramer法则,可以得到结果以及对和集电极的电压如下所示
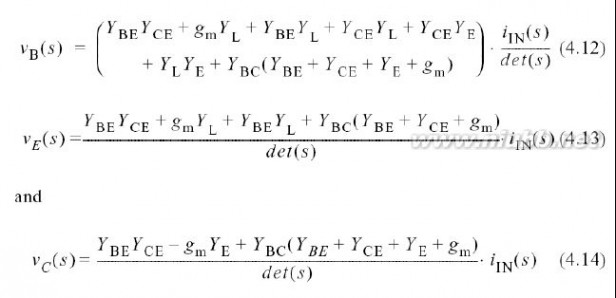
: 的响应.因此,在基极,发射极
导纳矩阵的行列式写作
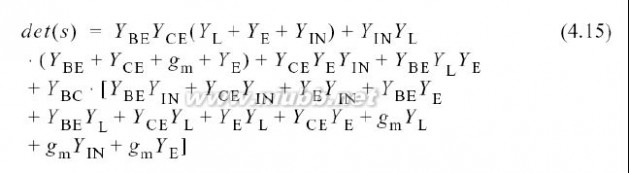
:
基极到发射极,
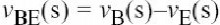
集电极到发射极的电压分别是.最后,
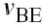
由于成分产生的失真,很容易得到它们的比值: 和经常用于计算失真,例如由gm和
volterra 第四章Volterra模型

线性化分析的目的是为了获得所有非线性元件的基本电压幅度,这样我们就可以继续计算这些元件内部产生的非线性电流.在此之前,我们需要对信号摆动进行一些观察.
BJT的指数响应是极端的非线性,并且在没有过度失真的情况下,不能承受高于10到30 mV的信号幅度.这听起来不像一个功率放大器,但是两件事情恰好帮助改变此情况.首先,器件并不是完全指数的,但是当驱动到高注入时,BJT线性化可用(4.1)中的参数IKF来模拟.第二,放大器有一些反馈机制来减小BE结中的信号电平.串联发射极阻抗引起一个线性化的串联反馈,CBC引起一个并联反馈.CBC的作用十分重大,这是由于强烈的电容性反馈降低了基极阻抗,因此也减小了BE电压摆动和从驱动激励产生的失真数量.
4.3.2非线性分析
在本节中展示了一个CE BJT放大器的非线性模型,并由它得到IM3失真.该电路有三个两输入和一个三输入的I-V和Q-V非线性,通过鉴定7个一阶系数,二阶系数和三阶系数模拟得到,其中18
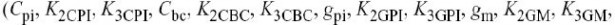
个是电系数
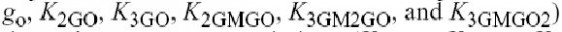
,其它9

个与动态温度变化相关
.
最后,此分析将介绍IM3音调,它是一个矢量和,由以下组成:7个由立方电非线性引起的项,21个由级联二次方非线性(修正包络信息向上转换到IM3中)引起的项,21个二次谐波向下混合到IM3的项,最后,5个立方的和24个级联的二阶电热项.这些看
volterra 第四章Volterra模型
起来也许很多,但它描述了产生失真的不同机制的真实幅度;它同样清楚地证明了,只要立方项是解析的,大量的信息就会失去.若电路较大,分析的阶数越高,则需要对数据进行压缩,但是原理还是一样的:我们希望知道,通过从直流或谐波波段混合失真并使总失真最小化(或最小化其记忆效应),能产生多少IM3总数;我们希望知道在这些谐波波段,由失真电压引起了什么样的非线性和实际阻抗.
由于项数众多,我们不单个地对这些项进行讨论.完整的分析见附件C,接下来用一些例子讲述计算步骤.
4.3.2.1二阶失真电流
图4.8所示的电路用于解决二阶响应,图4.7中的线性输入电压在此被短路, 添加二阶失真电流源与所有非线性电路元件并行.以T结束的电流是电热电流,将在第4.3.2.5节中讨论.如同以前, ZIN, ZE和ZL将包寄生,偏置阻抗和匹配阻抗结合在一起.
为了计算自我加热效应,瞬时功耗用
热阻抗用于计算频率ω2–ω1
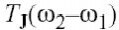
处的瞬时温度波动计算,第3.4节所示的.可以对不同的电路元件使用不同的温度,但是它们在物理上靠近基极区,此处使用共同的温度.然而对于大型设备,将此设备分成较小的并行设备是十分有利的,这样可以看出不同的温度变化.
非线性被模拟为和,和温度组成的三维函数,它包括和是基极到射极电压和非线性以及所有高达三阶的交叉项. 温度的函数,非线性由集电极到基极电压和温度控制.
volterra 第四章Volterra模型
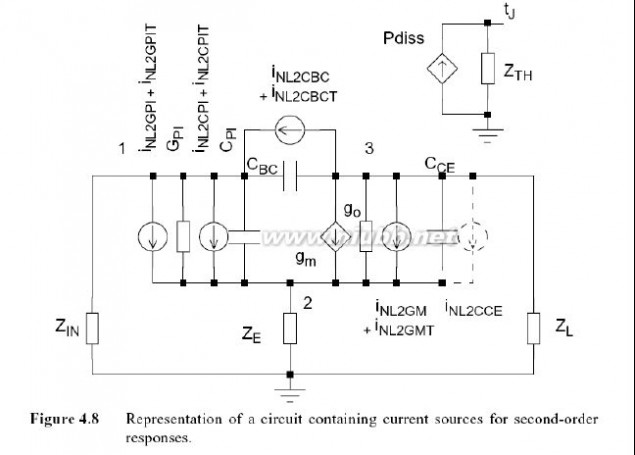
图4.8 含电流源电路的二阶响应表示 我们通过计算二阶失真电流
ω2–ω1处由开始进行分析.举一个例子,在引起的二阶包络电流是:使用表
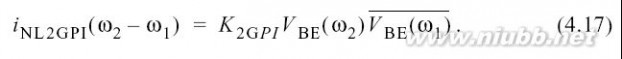
2.5
举另一个例子,
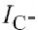
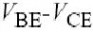
由非线性引起的二阶包络电流是
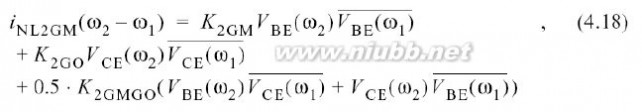
:
它结合了二阶输入非线性
入输出交叉项,

输出非线性的作用,见I-V模型(4.3). 和输从表2.5中可以看出,相量频率和可能的常量项值的选择取决于音频:例如,
volterra 第四章Volterra模型
的乘积在2ω1处产生一个音调.上述的相量音调被选中,所以
能在包络频率ω2–ω1产生失真.计算基频ω1和ω2的相量(4.12)-(4.14)式. 和用
4.3.2.2跨导倒数转移函数和二阶电压
接下来,我们需要把不同结点的失真电流转换为失真电压.此处,我们选用了一个象征性的分析,因此很容易得到从结点X和Y到结点Z之间的非线性电流源的转移函数。(www.61k.com]大概的想法是:在每个非线性元件中,失真电流的幅度用较低阶的电压相量计算,并使用转移函数,然后在所选择的结点上,所产生的失真电流被转换为失真电压. 转移函数可从(4.11)中得到,
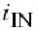
只需将
例如, 转移函数的形式为
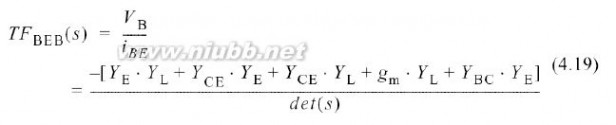
: 用结点X和Y之间的一个测试电流源代替即可.
det(s)由(4.15)得到.附件C中给出了一整套转移函数.通过使用这些符号,基极结点处完整的二阶包络电压为:
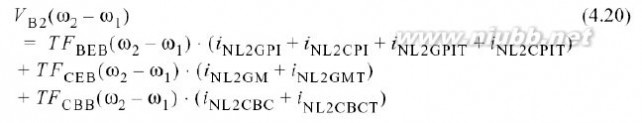
其中,每一个失真电流源乘以合适的跨导倒数(在基极将电流转换为电压).同时需注意,式中有8个不同的电流源(基中的4个是电热的电流源,用T标识),每一个电流源都有一个等式,类似于(4.17) 或(4.18).
为了解决二次谐波电压,
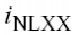
我们需要将需要的谐波的源的电流等式重写,并在相对频率下重新计算(4.20)式.在此步骤之后,基本包络和二次谐波音调是八个
volterra 第四章Volterra模型
不同成分的总和.通过对这些成分分别存储,我们可以看出哪个是主要的,哪些互相抵消.
4.3.2.3 解三阶电压
接下来,我们要计算IM3在频率为2ω1–ω2时的集电极电压.三阶分析采用与二阶分析完全相同的等效电路,集电极电压用下式计算

:
其中,音调2ω1–ω2的失真电流被计算, 转移函数(同样在2ω1–ω2频率点计算)被用来将X-Y端口的非线性电流iNL转换为集电极电压.然而,与二阶分析相比,非线性电流源的等式更加杂乱,这是由于IM3电流不仅由立方非线性引起,同样由级联的二阶非线性引起.例如,根据表2.6,IM3电流中出现的包络电压和二阶谐波是由非线性引起的
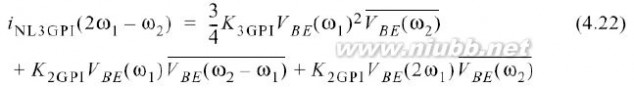
.
相似的响应也会产生,
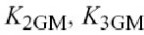
例如通过系数对非线性的
下列的附加项:
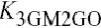
.除开这些之外,
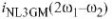
输入输出交叉项给, 和 和带来
volterra 第四章Volterra模型
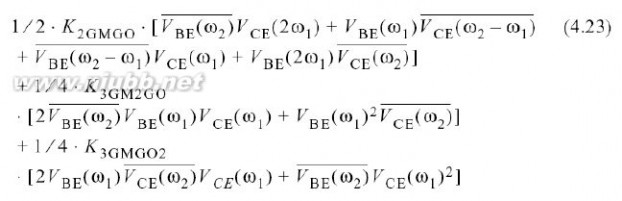
其中,所有线性和二阶输入输出电压的结合如上式所示,且它们的产物在2ω1-ω2处形成一个音调.注意到,在交叉项中,所有可能的排列是必要的.例如,等式(4.23)中的最后一项由在频率ω1, ω1和–ω2处的一个VBE和两个VCE电压组成, 它们可以排列成下面的三个结合: (VBE(ω1), VCE(ω1), VCE(–ω2)), (VBE(ω1), VCE(–ω2), VCE(ω1)), and (VBE(–ω2), VCE(ω1), VCE(ω1)),其中,前面的两个的结果相同.数字频谱卷积可以自动地给出所有的组合.
现在,根据基本结点电压和二阶结点电压来描述IM3.接下来,我们更深一层地讨论失真,失真仅作为基本输入电压的函数.这使得表达式变得十分复杂,但也带来了一个好处,就是能维持二阶失真电压的原始信息.
4.3.2.4 IM3仅表示为基本输入音调的函数
为了将失真仅表示为输入音调的函数,我们需要做两件事.首先,
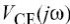
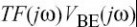
写作
,TF可由(4.16)和附件C得到.其次,将所有的二阶音调根据基本输
入写出来,这会产生总共42个级联的二阶项,都列在附件C中.
(4.21)式的纯立方部分根据
表2.6,作为

一项被
被
表示为和被写入到(4.24)式中.在此,非线性电流根据的函数被写出来.例如, (4.24)的第的乘积所控制.
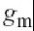
输入非线性值所控制,交叉项被输入和输出电压所控制.
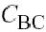
对于. , ,电压和仅必须被
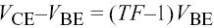
volterra 第四章Volterra模型

由级联的二次电非线性引起的IM3等式变得十分复杂,整个的等式包括21项从包络得到的混频产物,21项从二次谐波得到的产物,如附件C所示.这里列举这样的一个例子,由K2GM*K2GPI引起的双重混频.组成如下
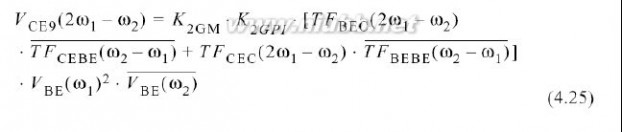
:
此等式包括两种低频混频结构,如图4.9所示.图4.9(a)描述了第一种结构, 在
中,

ω1–ω2,然后通过
电压和和的乘积在集电极和发射极之间产生包络电流,被转回到基极到发射极电压.这些包络电压和基本在中再次混合,在基极和发射极间
,它们被转换为集电极电压.
和在K2GPI的2ω1–ω2处产生IM3电流.通过转移函数第二种结构如图4.9(b)所示,可以这样解释:
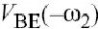
基极直接产生包络电流ω1–ω2.此电流在基极和发射极之间的部分通过
被转换为基极到射极的电压,因而产生的包络电压与基本基极到射极电压在中进行混合,因而在集电极和发射极之间产生了IM3电流.最后,该电流
volterra 第四章Volterra模型
通过被转换为集电极电压
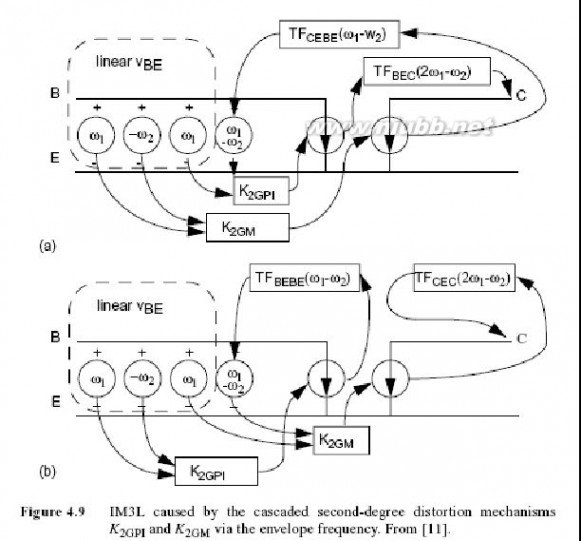
.
图4.9 通过包络频率,由级联的二阶失真结构K2GPI和K2GM引起的IM3L 诸如此类的多重混合产物实在是常见.例如,在AB或B类放大器中,引起IM3的一个主要原因是:当消波不均匀时,晶体管会在输出产生一个高的二次谐波(由高
来模拟).由于二次谐波的频率很高,通过CBC回到输入能很容易地耦合,并且在
称为中与基波再次混合,导致输出端直接有IM3电流.这种结构(在附件C中项)能通过衰减集电极或基极的二次谐波来将其最小化.
4.3.2.5电热项
最后,描述了三阶电热失真结构.
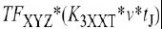
这由三阶项和级联二阶
volterra 第四章Volterra模型
项组成,其中,热感应二阶失真与基频混合在电平方律非线性中.三阶项可表示如下
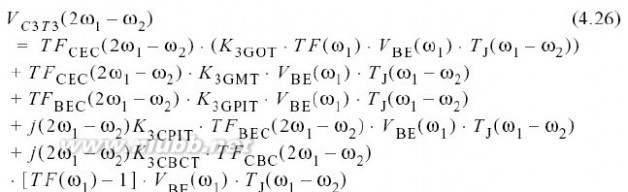
:
其中, 是结温,TF是比, 是从非线性源到集电极的跨导倒数. 需注意到,模式是一直不变的:低频温度变化调制电路元件值,使其与基频音调相混合.结温的计算是基于耗散功率
仅仅包络音调,这将产生一阶和二阶音调,
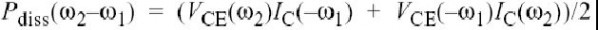
被精选下来,并与热阻相乘以得到结温的变化.耗散源是一直不变的,但是如果不同的电路元件需要不同的温度,热网络可以用Z矩阵来模拟. 级联的二阶非线性IM3成分同样很复杂,在此不详述,见附件C,并且它们的数字值在第4.4.2和4.5节中用矢量图表示.需注意,包含由温度决定的电荷项
不能被计算,除非找到一个测量它的值的方法.
由上文和附录C可见,对一个简单的CE放大器的符号的Volterra分析变得十分棘手,许多复杂的拓扑很难对其解析地进行分析.然而, Volterra计算可用数字计算来进行. Nlsim软件[24, 29]能够用数字计算非线性电压元件,并且能对更复杂的拓扑进行分析.与完整的解析方法相比, Nlsim对失真的描述稍微粗略,且不分开级联的二次非线性,但是它能简单地显示每一个非线性的立方项以及向上,向下转换包络和二次谐波项.不论如何,二阶相量可以被划分为矢量的和,从而看出哪一个是主要的二阶成分.
4.4 BJT CE放大器中的IM3
volterra 第四章Volterra模型
在这里,我们研究两种不同案例下的IM3失真:首先,使用一个将非线性输入和I-V曲线级联起来的简单模型,然后用全电路,包括反馈效应,采用前面章节所描述的全分析.
4.4.1 BJT作为两个非线性方框的级联
如前文所讲,BJT放大器的失真成分十分复杂,因此,需要首先做些简化来找出失真成分的基本特性.之后将会给出一个完整的分析,

但是暂时忽略发射极阻抗
反馈电容和
产生的反馈影响,并简单地认为集电极电流是一维的,仅受基极电压的作用.图4.10给出了简单的电路,由于所有的反馈效应被忽略,BJT的集电极电流可以被简单地认为是两个非线性方框的级联,如图3.5所示.第一个方框包含输入非线性Cpi和gpi,第二个方框包含一维跨导的非线性.
我们知道,当采用电压激励或电流激励时,CE BJT放大器的线性特性是不同的.在理想化的情况下,零的电压激励使得输入非线性可以忽略不计,这是因为输入和基极到射极电压是相等垢,并且电压源使得所有失真电流短路.于是图4.10中唯一有效的非线性成分是跨导.如果采用电流源激励,情况就会改变.图4.11(a)指出基极到射极电压是输入电流的函数,图4.11(b)描述了集电极电流,它是基极到射极电压的函数.图4.11(a)可以看成是一个对数函数,图4.11(b)是一个指数函数,作为它们的级联,集电极电流是输入电流的函数,是一条标准的直线,如图4.11(c)所示.因此,当晶体管受电流驱动时,被电压驱动的BJT的强大的指数非线性消失了.同样,在实际中,激励的类型可以通过适当调整ZIN值来改变: ZIN的值越高,CE BJT就越表现为由电流驱动.
volterra 第四章Volterra模型
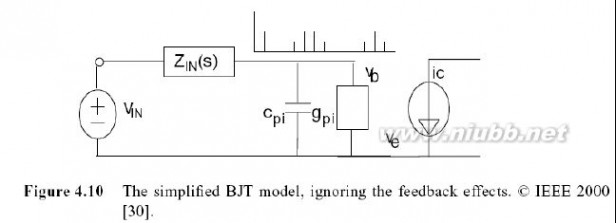
图4.10 简化的BJT模型,忽略了反馈的影响
图4.11中,两个相反的非线性相互抵消.同样的现象也在图4.12Gummel图中被证实,其中,集电极和基极电流是的函数.由于采用了一个对数的Y轴,这些完全地指数非线性表现为直线的形式.可以观察到,线之间的距离(例如电流增益)是常数且不依赖于的值,这表明,非线性的形状是相似的.
这种两个非线性相互抵消的现象通常称为跟踪非线性,结果导致非线性元件线性工作.然而,在实际中,非性线特性不能完全地进行跟踪,结果是一些非线性经常存在.例如,图4.12中线的虚线部分表示了实际情况:跨导在高值时不再是纯指
值数的,这是由于在基极有一个高注入电平,因而减小了电流增益.同样,在低
处,一些基极泄漏电流经常存在
.
volterra 第四章Volterra模型
图4.11 跟踪非线性的描述
(a) 是 的函数(b) 是
的函数
(c) 是的函数
接下来,将分析图4.10所示的电路的交流特性.第一个方框的非线性是由gpi 和 Cpi引起的, gpi被认为是完全的指数的, Cpi也认为是指数的,从前向传输时间( )和跨导gm来计算

:
后面的方框描述了非线性跨导,它的非线性可以用(4.1)来计算.如果我们忽略早期效应并仅使用一维的集电极电流,就可以得到如表4.2所示的非线性系数.表中第二
列对应于严格的指数低注入的情况,第四列出示了一种高注入的情况,在这种情况下, 跨导的非线性减小,见图4.12中虚线部分
.
图4.12 基极和集电极电流,作为基极射极间电压的函数.曲线的虚线部分表明高注入和漏电流效应
表4.2 跨导的非线性系数
volterra 第四章Volterra模型

在第三章中已经讨论过级联的非线性失真成分,并在图3.6中加以描述.级联的IM3L集电极电流为
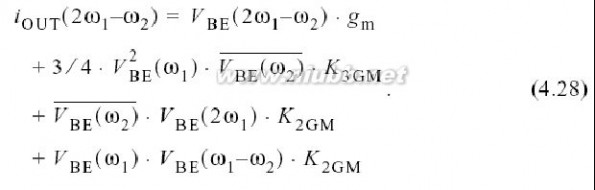
:
IM3L由4项组成,前两个分别由第一第二个方框内部直接产生.后两个涉及到二阶交感,通过方框间的包络和二次谐波频率产生.在第一个方框中,失真是由输入阻抗的二阶非线性产生, (4.28)中基极的频谱成分可用表2.6计算.
首先研究图4.10电路中基本的作用.非线性系数用等式(4.1)和(4.27)计算,基于BFG11射频功率BJT[32]的GP模型SPICE参数.在中心频率1.8GHz和音频间距1MHz处计算IM3电平.如果与内部基极电阻相比,输入阻抗的值较高,输入将表现为一个电流源,并且输入输出非线性将会部分地进行互相抵消.
在整个合理的值上,在基波的
被扫描,用以检查电压/电流激励的作用.BJT的输入是变化的匹配,这说明输入电抗已被确定,所以基极电抗关断
volterra 第四章Volterra模型
.在谐波和包络处的值被设置为无限大,这说明
在这些频率处的基极阻抗仅由内部基极到射极阻抗组成.图4.13中显示出在集电极电流两个值处的IM3失真成分,它是基波的函数. 图4.13中同样显示出IM3的不对称性(例如,低边带和高边带之间的矢量误差)
在低注入的情况下,通过将
加值增加到20 到30 ohms来提高IM3值.继续增值,并不再减小IM3,因为输入非线性和输出非线性之间的不完整跟踪,将IM3
,情况有所
,在一些相关的低值处,仍
的优点是在最适宜的限制在–57 dBc,如图4.13所示.在高注入的情况下不同:尽管在此情况下,
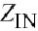
线性并不十分依赖于高值的可以达到线性的重大提升.与拐点电流IKF相比,
较高的处,线性得到较好提高.
当基波的虚部开始从共轭匹配的情况下增加时,线性开始恶化,即使它可能稍微地减小,IM3边带间的矢量差(例如不对称性)可能减小.图4.13中较低的曲线表明了低IM3音调和高IM3音调之间的不对称性.通过使输入匹配稍微是感应的,在IM3边带对称性上可以有多于10 dB的提高. [33]中也有相似的观察,其中研究了输入阻抗对相位失真的影响.对称性的提高对于包括线性在内的应用而言,是一个非常重大的提高.
volterra 第四章Volterra模型
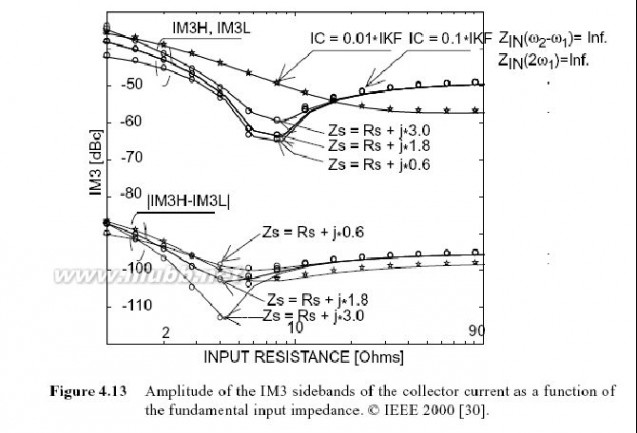
图4.13 集电极电流IM3边带的幅度,它是基波输入阻抗的函数
由于大量的输出三阶失真是通过级联的二阶非线性产生的,所以对带外的仔细优化能提高线性.三阶项不会被滤波影响太多,这是因为它们的功率与基波信号交迭,但是二阶信号的功率位于基波较远的地方,且可以通过使用滤波来达到最佳可能的线性[27, 34-36]. 同样,例如增益和效率的基波匹配也有许多要求,因此基波阻抗的选择,不能只基于线性特性.然而,带外匹配仅对增益和效率产生次要的影响,因此,有时可主要依靠线性来调谐带外匹配.
现在,我们来研究二阶信号成分的作用.当在包络被扫描时,基波周围的阻
and )引抗保持常量.在图4.14(a)中,较高的八段向量表示由输入非线性(起的输出IM3产物,而低三段向量的前两个向量表明输出三阶IM3产物是由二阶输入输出非线性引起的.这两个中的第一个是通过基极的包络产生,另一个是通过二次谐波产生.低三段向量中的第三个表示跨导的立方非线性.有趣地注意到:由二次非线性引起的IM3向量部分,与由立方非线性引起的向量部分相反.这表明,非线性间的互相跟踪有两种方法:第一种是通过前面讲述的输入输出跟踪法,这种方法表明,基极
volterra 第四章Volterra模型
的失真电压波形抵消了由非线性跨导引起的失真;第二种方法是通过二阶和三阶非线性间的抵消.由于使用了大量的转移函数,后面的这种方法在本书中较难用等式来表示.然而,如果我们忽略Cpi,并根据(4.29)中的电路元件和系数写下三次谐波电流的表达式,可以清楚地看到,二阶和三阶系数的符号是相反的.
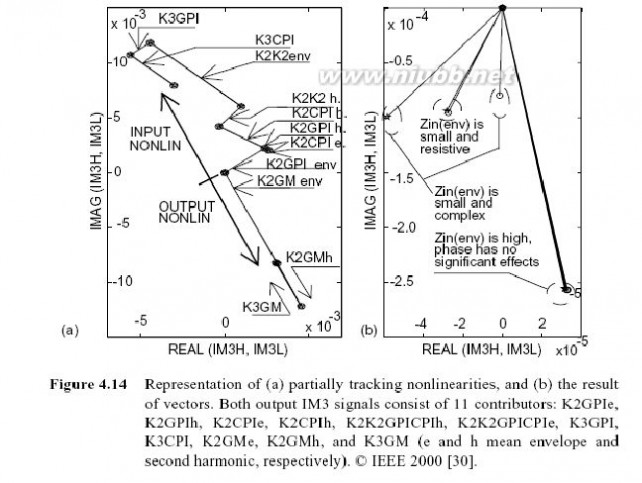
图4.14 (a)部分跟踪非线性的表示(b)向量结果. 两个输出IM3信号由于11部分组
成…..(e表示包络,h表示二次谐波

)
图4.14(b)描述了包络处四个阻抗值的IM3结果(由部分跟踪非线性引起).如
volterra 第四章Volterra模型
果阻抗幅度高,输出IM3信号将不被其相位所影响,但是如果阻抗幅度相对较小,至多比基频处的
处的高10,其相位将会起着重要的作用.为什么仅在较小时,包络对IM3有影响的原因十分简单:

如果高,基极结点的总阻抗受晶体管内阻抗的控制,但是当小时,它却影响整个结点阻抗.
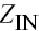
的方法来减小总体失真.从上面可以看出,这并不
值,或者提高IM3边带间的平衡来减小总体
(ω2–ω1)又混合到不同边
在高IM3边带和通常建议用最小化低频常用;然而,可以用一个较小的假定失真.既然失真电流与 (ω2–ω1)
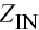
相乘,而带中,
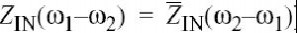
且它们的阻抗相位相反
低IM3边带间,当纠正相位错误时就会得到一个小的反应基带偏置阻抗.
4.4.2 详细的BJT分析
现在,我们使用完整的Volterra模型来研究单个失真结构的作用.在这种情况下,模型的非线性系数是通过实际测量得到,其采用的步骤在第五章中将会有详细的解释.在本节中,我们研究CE BJT放大器线性上不同频率处的偏置点和优化终端阻抗的作用.
大家都知道,CE放大器的最佳阻抗随偏置情况而变化.如果我们用实验的方法来检查所有可能的基波输入和负载阻抗在不同偏压点的结合,并且也考虑包络和谐波阻抗(对线性影响很大),那么,单个CE级的优化都会变成一项十分冗长的工作. Volterra模型(假设它足够精确) 通过在不同偏置情况下设计最佳输入和负载阻抗,被用来优化CE放大器的线性.
一个基于BFG11晶体管的放大器[32]被建造,并且在基频1.8 GHz处的输入阻抗被调谐成共轭匹配以用于最大功率转换.负载阻抗已确定,因此输出电抗的虚部和匹配网络在外部相互抵消, 且的实部由期望的I-V特性所决定.可以通过降低值来提升线性,这是因为集电极的电压摆动减少了,但不幸的是,同时效率也有所减小.所以在线性和效率之间,选择20 ohms作为的平衡值.零频率附近的负载阻抗
volterra 第四章Volterra模型
很小,这样可以从电流源提供直流功率给集电极且损耗最小.放大器在二次谐波处的输入和负载阻抗分别是0.1+j76和31+j17,在包络频率为2MHz时, 输入和负载阻抗分别是13–j0.2 和0.2–j1.4.这些数据都是由实际的放大器测量得来.
首先扫描基极和集电极偏置电压,并且监测线性以便找出偏置的一些基本特性.为了使仿真之间有可比性,输入电压摆动和负载阻抗仅被稍微调谐以保证在变化的偏置情况下,输出电压和电流摆动是常量.选择输出电压摆动为1.5 Vpp,这意味着在集电极电源附近的IM3值低于1V是不精确的.图4.15(a)描述了计算的IM3L曲线和测量的IM3L点,可以看出,它们相互之间有着很好的相关性.
在偏置电流为75 mA时,线性最大,当偏置电流减小时,线性开始恶化.当偏置电流降低到40 mA时,IM3边带增加约10 dB.集电极偏置电压同样也影响线性,因此在电压值为3.5V时,线性最大.图4.15(a)中没有显示出超过4V的集电极电压,因为高的集电极电压仅仅减小了效率并没有更远地提高线性.电流较低时,线性彻底不依赖于集电极电压,但在高电流值时,集电极电压却起着非常重要的作用.这是显而易见的,因为在低电流值时,由gpi, Cpi和gm
引起的非线性比由 和 交叉项引起的非线性要强.此外,在高电流值时,非gpi, Cpi和gm引起的非线性较弱,这是因为跨导的原因,例如,由于高注入作用产生的电流线性化.同时,既然
值的情况下十分强大,对于总体失真来讲, 和其非线性在高集电极电流起着更主要的作用.
volterra 第四章Volterra模型
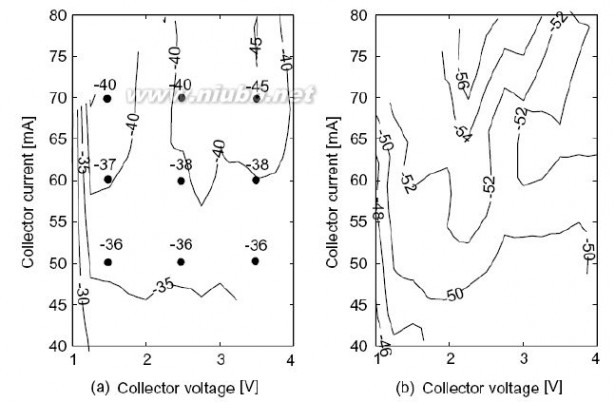
图4.15 (a)计算的和测量的(网点)IM3L(b)测量的非对称IM3L-IM3H
IM3H边带的轮廓点图与IM3L的十分相似,如图4.15(a)所示.边带间的向量差用dBc描绘出来,以便与基波信号作对比, 如图4.15(b)所示.需要重点强调,此图形不仅取决于偏置值和匹配阻抗,它也取决于调制频率.如果采用预失真的线性化方法,边带间的非对称性是一个重要的品质因数,如第三章所讨论.
在前面的例子中,选择基波输入和负载阻抗的值,用来达到需要的功率和有着合理效率的增益特性.然而,为了达到可能的最佳优化,必须对带外包络和谐波终端进行优化.通过调谐带外终端来提高线性的一个最常用的方法是,使得二次谐波处的负载阻抗最小化.既然部分的IM3成分是由二次谐波电压引起的,在此频率处的阻抗也影响IM3.而这些是否有助于线性的提高取决于非线性系数和其它的阻抗.为了检查二次谐波匹配的效果,在那点频率上的负载阻抗的实部被减小到6 ohms.比较的结果见图4.16,它指出了在所有偏置情况下从1 dB 到 5 dB的改进.这些计算指出,为了达到最佳性能,带外阻抗需要进行优化.这里仅证明了二次谐波负载阻抗的影响,但是其它的带外影响同样重要.经选择的最优带外终端阻抗可以将线性提高几分贝,而不减小基波的功率和效率性能.
volterra 第四章Volterra模型
如第三章所述,IM3边带间的不对称性受包络阻抗的严重影响.在多载波发射机中,信号的带宽可能很宽,例如,在直流和20 MHz间很难设计常量阻抗.输入和负载包络阻抗通常不是常量,由于IM3边带是这些阻抗的函数,它们随调制频率而变化,从而引起记忆效应.
通过扫描一个双音信号的音频间距(集电极电压是3V,基极偏置电压是740 mV),我们来研究记忆效应.用Volterra计算的IM3L的相位如图4.17所示,它是音频间距的函数,并且符合三种不同类型的记忆效应:低频处的热记忆效应,共振型的记忆效应以及高频记忆效应,后两者皆由偏置电路引起.
在1 MHz处的谐振由一个谐振集电极阻抗引起.使用Gummel-Poon (GP)模型不能观察到谐波平衡仿真,因为其过分简单的输出阻抗掩饰了集电极谐振的效果.在高调制频率处的平滑相位偏移是由包络频率处的输入阻抗引起的,仍然是使用GP模型进行模拟.由于动态的自我加热效应在基本的GP模型中不被执行,就不能预测由热效应引起的低频记忆效应.
Volterra模拟适合所测量的结果,如图4.17所示,第六章会有更详细的说明.因此, Volterra模型似乎是一个更好的工具,用来确认功率放大器的记忆效应.
volterra 第四章Volterra模型
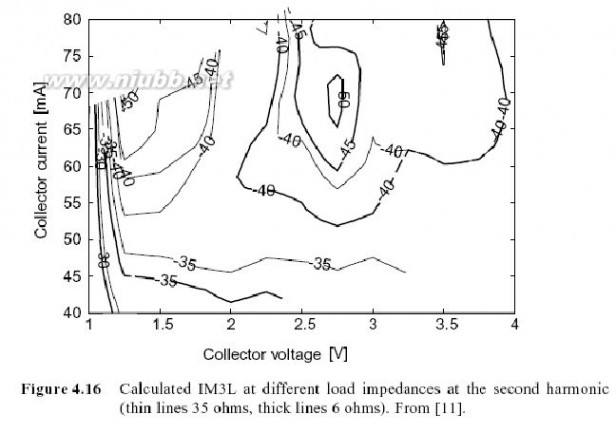
图4.16 在二次谐波不同负载阻抗处计算的IM3L(细线是35欧,粗线是6欧) 接下来,我们研究IM3相图的微细结构.此信息可以用来进行设计优化,此处所画的IM3是作为十个组成项的矢量和,以便用来研究为什么IM3L的相位取决于调制频率.我们选择三个频率点来画矢量图,分别是100 kHz, 1 MHz,和1.1 MHz,并研究1 MHz处的谐振和热记忆效应.
volterra 第四章Volterra模型
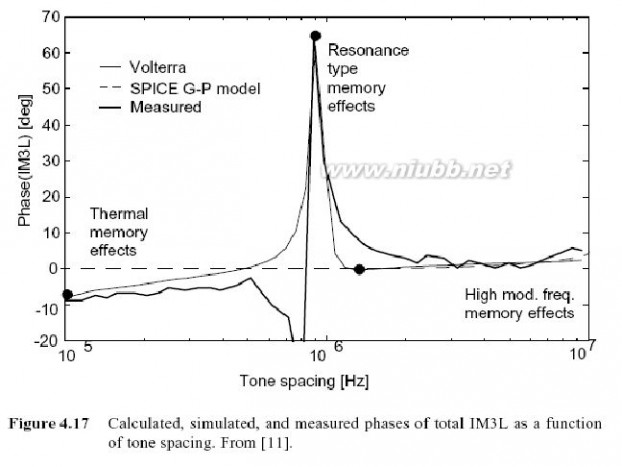
图4.17 总IM3L计算的,模拟的,测量的相位,相位是音频间距的函数 我们首先来看看,在音频间距为1.1 MHz的谐振上发生了什么.在图4.18(a)描述了IM3L相量,它是实轴虚轴上一系列相量的和,从图中项端的中心开始.此相量由49个纯电气项组成,前面的7个由立方非线性引起,后面的42个由级联的二阶非线性通过包络和二次谐波频率引起.电热项几乎是零,因为1.1 MHz的差频频率已经位于热滤波器的衰减带中.
前面的7个点(1-7)是立方失真机制,其中 (6)最大.接下来的21个点 (8-28)是由包络频率得到的向上转换的IM3成分,最后的21个点(29-49)是由二次谐波得到的向下转换的IM3成分.这是由于一对对之间部分地进行相互抵消:三阶非线性和部分的抵消,同样的, (29,其中二
(37,由混合在
(45,二次谐波由混合在次谐波由返回到输入进行再混合的gm产生)和中的gm产生二次谐波),
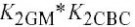
或者
volterra 第四章Volterra模型
中的gm产生)和生
) (48,

二次谐波由被放大并混合在中的Cpi产
volterra 第四章Volterra模型
图
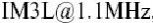
4.18 (a)
(b) 和的向量表示
之间的向量差
成比例的失真在基本处被转换为电压, 怎样可以提高线性呢?与

并且它的组成成分(6)

可以通过调整的相位,朝着原点旋转;可以通过降低二阶谐波阻抗来减小整个29-49网孔的大小.另一方面,二次谐波处的基极阻抗可能会增加5%到10%,从而使得总和更加接近于零.
从记忆效应的观点来看,当音频间距减小到1 MHz时,研究会发生什么情况是十分有用的,刚好会遇上ZL内的谐振.这在图4.18(b)中被论证,它表明, IM3L@1.1MHz和IM3L@1.0MHz的差是一个相似的相量和.首先,由于基波单调的相位不变,立方非线性(1)-(7)表现相同. 二次谐波的混合产物(29-49)同样是相等的,这表示二次谐波的终端阻抗是平滑的.所有这些引起IM3谐振的决定性原因是由于级联的二次非线性,它向上转换包络频率—大的项包括
的输出包络), (24,
混合到
(26,
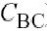
被放大并混合到
基带频率响应.
接下来,我们研究在音频间距为100 kHz时,由电行为和热行为之间交感作用产生的记忆效应.图4.19中描述了用向量的第一段表示的纯粹的电IM3向量,在如此低的频率下,它们几乎都是一样的.电热的三十段向量用逐项列出的方法显示,且可以看出电热失真是由K3GMT, K2GMT, K3CPIT和K2CPIT项控制.
然而,需要注意IM3L和IM3H间的大的相位差.这仍是因为基带效应,包括热反馈,与相反的相位混合到较低的和较高的IM3边带中.除了相位的不对称性,热反馈同样引起了IM3L和IM3H之间幅度不对称,这是因为原点和终点78之间的距离对于IM3L和IM3H是不同的. (14,混合到里的输出包络), 的中的输入包络,这些都包括了
volterra 第四章Volterra模型
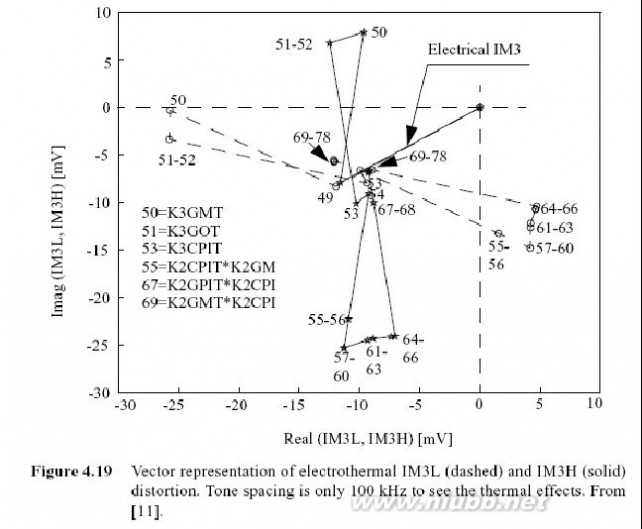
图4.19 电热IM3L(虚线)的向量表示和IM3H(实线)失真.音频间距仅为
100KHz,用于观察热效应
4.5 MESFET模型和分析
从本节中,可以得到一个MESFET共源极放大器的Volterra模型.如图4.20所示的一个小信号等效电路,电路包括一个输入阻抗
部级数栅极阻抗组成),一个栅极到源极电容
漏极到源极电容
抗,
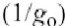
一个阻抗,跨导
(由驱动阻抗,外部输入阻抗和内,
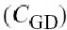
一个反馈电容,负载阻抗,一个和电源阻.在BJT的情况下,输入和负载阻抗不仅包括匹配网络的阻抗,同样也包括偏置网络的阻抗.FET的漏电流可以被模拟成一个三维的函数,此函数是栅极电压和漏
volterra 第四章Volterra模型
电压,以及温度的函数,形式类似于
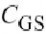
(4.3). 和同样被认为是非线性的,它们分加是栅极到源极电压和温度的函数,以及漏极到栅极电压和温度的函数

.
图4.20 共源极FET放大器的线性化一阶电路
图4.20所示的共源极FET放大器的线性化电路与图1.7所示的BJT放大器非常相似.通过忽略并改变电路元件的名称,在第4.3.2节中推出的等式可以用于FET分
和它的非线性电流源,可以得到一个包含失真源的FET电路,析.同样的,

通过省略
如图4.21所示.器件的非线性特点是有个一阶的,二阶的和三阶的非线性系数,其中15个是纯电的系数
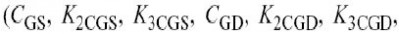
(
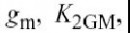
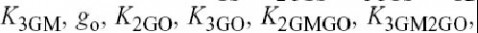
和),7
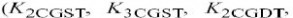
个与温度变化有关
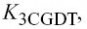
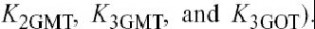
.等式(4.3), (4.6), (4.24),
(4.26), (4.28)以及附件C可以用于FET的简化,可需忽略
成GS和BC到GD. 并将电压和下标BE改
通过使用S参数特征法,可以得到Infineon CLY2 GaAs MESFET [37]的电路元件
volterra 第四章Volterra模型
和非线性系数,这种方法将在第五章介绍.表4.3列出了由实用放大器测量得出的输入阻抗和负载阻抗
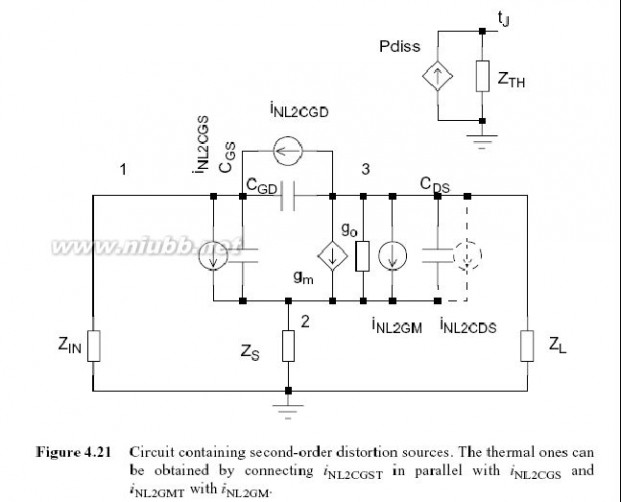
.
图4.21 电路包含二阶失真源.
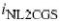
热失真源可以通过将和并联得到

. 和,
表4.3 不同频带处的输入和输出匹配阻抗
图4.22中的实线表示IM3的计算值,这些值是在偏置电流和电压在中心频率为
volterra 第四章Volterra模型
1.8 GHz,调制频率2MHz,以及输出电压摆动为2 Vpp时得到的.在整个I-V平面,可以看到线性变化最大超过30 dB,但是由于直流功耗根据线性,随着偏置点而变化,所以在效率线性转换方面并无重大提高. Volterra计算与测量的线性值之间是适应的,如图4.22中的点所示.
接下来讨论带外阻抗的影响.将包络频率处的输入阻抗值从1.3k–j1.3k增加到10k – j10k以观察偏置阻抗的影响.从图4.22中用虚线表示的新的线性等高线可以看出一些重大的改变.在漏电压较低时,线性减少了少许分贝,但是在电压为4V,漏电流为150 mA时,线性提高多于10 dB.然而,由于
4.22所显示的提高频带十分狭窄.
图4.23描述了由包络频率处调制栅极电压引起的变化,其中,在 VD=4.5V 和 ID=150 mA的偏置点处,计算两个基带输入阻抗的IM3向量(音频间距为2-MHz),如图
4.22所示.总失真由立方失真机制K3GM, K3GM2GO, K3GMGO2和K3CGS所控制,这些机制间的抵消如图所示.交叉项的作用(特别K3GM2GO)是十分重要的,大部分是由于I-V特性.然而,高
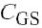
处的提高是由于(项,只表示为
产生的包络电流,然后,包项. 高度依赖于频率,图):
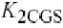
较大的栅极阻抗放大了由络电流在再次混合到IM3,如图4.23所示,

它几乎抵消了大的
volterra 第四章Volterra模型

图4.22 在包络频率处,输入阻抗的两个值上的计算的IM3L轮廓(用线表示)和测量的IM3L轮廓(用点表示),单位是dBc.中心频率是1.8GHz,调制频率是2 GHz,输出电压摆动是2Vpp.
[39]中研究了包络频率处的栅极阻抗的影响,其中,通过实验证明,线性的改变是由栅极阻抗的改变引起的. [40, 41]中通过测量证明基带漏极阻抗也会产生同样的影响.在[39-41]中的所有情况下,最合适的栅极阻抗和漏阻抗都较低,但这里指出,最优包络阻抗可以高或可以低,这都决定于非线性结构的幅度和相位角.[35]中同样也讲述了最优非零包络阻抗.总的来说,带外阻抗可以用来优化失真,并且能预测IM3性能会有一个大量的提高.通常,带外阻抗所带来的影响总是不受欢迎的,这是因为包络阻抗(大部分由直流偏置电路引起)在一个范围较大的调制频率上不会是常量.由于IM3成分受包络阻抗的影响,将会产生记忆效应.
volterra 第四章Volterra模型
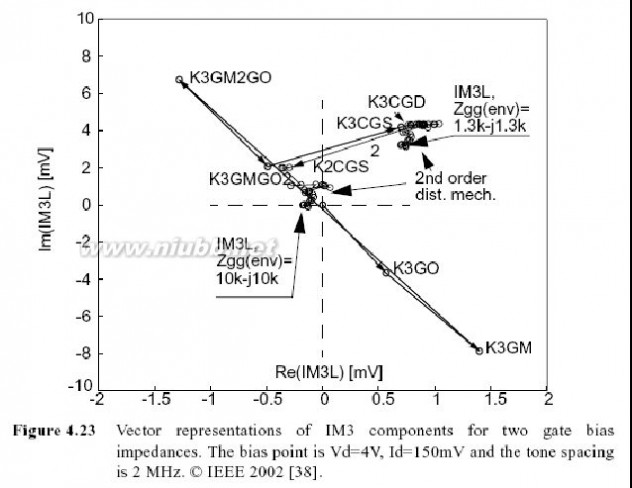
图4.23 两个栅极偏置电阻的IM3成分的向量表示.偏置点在
间距为2MHz. ,音频
为了研究记忆效应,我们再次采用Volterra模型模拟音频间距扫描.如图4.24所示,IM3L和IM3H的相位与测量结果有着较好的一致性(第六章中详述).在500-kHz音频间距时同样存在一个缓冲,是由包络漏极阻抗谐振引起的,在高音频间距处的相位漂移是由基于频率的基带栅极阻抗引起的.在一个单个的放大器内,相位的到
的变化当然不算严重,但在预失真功放中,它却足以减小15 dB以下的原本可达到的抵消,如第6章所示.
volterra 第四章Volterra模型
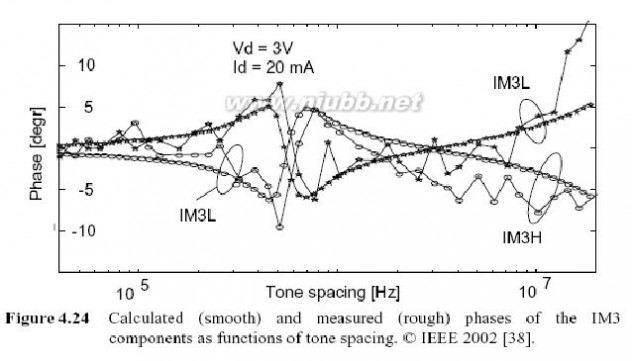
图4.24 计算的(平滑的)和测量的(粗糙的)IM3成分的相位,是音频间距的函数
4.6 总结
仿真模型的需求很具挑战性,并且由于所有的要求不能都被满足,模型被优化用来达到不同的目的.在多数晶体管/放大器的模型可以分成两类:行为模型和器件模型.行为模型仅仅设法模仿测量的现象而没有任何关于内部器件动作的信息,而器件模型或多或少地模拟了器件的物理动作.对器件模型的发展已经做了很多研究,但是对于射频功率放大器来说,这些模型并没有被完全优化.取而代之的是,大多数半导体模型,它们用来进行模拟IC设计,其中,运用了大范围的操作情况,对不同的尺寸来说,模型也必须是可升级的.从射频功放设计的角度来说,精确的失真模拟是必不可少的,同时,I-V和Q-V曲线的导数,以及自我加热效应也应该尽可能精确.不幸的是,仅仅一小部分供应商提供出成熟的功率晶体管模型的参数.
Volterra分析是小信号分析的扩展,电路元件的非线性通过多项式函数进行模拟,该函数是从期望的偏置电压周围得到的.通过这种方法,可以得到元件级的信息,并且在所选择的操作点周围,模型也是局部合适的,因此为模拟提供了良好的精确度.此模型和使用Volterra进行失真模拟分析的好处是可以得到IM3的成分信息:IM3可以画成一系列向量的和,每一个向量表示一个电路元件或混合结构的非线性.通过这种方法, Volterra分析提供了关于失真结构的洞察,并给出相关信息和可能的抵消
volterra 第四章Volterra模型
计划.对于优化匹配网络和选择合适的偏置电压点来说,这种方法十分有用.
本章中介绍的三阶Volterra模型可以用于BJT/HBT和MESFET共射极/源极放大器,只需作轻微修改.此模型包含一个非线性三维集电极/漏极电流,它是基极-射极/栅极-源极和集电极-射极/漏极-源极电压和温度的函数.输入电容Cpi/CGS是基极-射极/栅极-源极电压和温度的函数.反馈电容CBC/CGD是集电极-基极/漏极-栅极电压和温度的函数.在一个BJT模型中, gpi是基极-射极电压和温度的函数,无论何时晶体管用在高频时,它的影响都很小,其中Cpi主要控制输入失真.由于其它电路元件对总失真的影响较小,这些元件被认为是线性元件.本章中所讲述的模型同样包括反馈电容CBC/CGD和发射极/源极阻抗ZE/ZS,这些在之前发布的Volterra模型中已被忽略.电路被解析地进行分析,整个IM3元件的等式如附件C所示.
此分析中所用的集电极/漏极电流是其变量的泰勒级数,与大多数其它的Volterra模型相比,输入输出交叉项K2GMGO, K3GM2GO和K3GMGO2(对失真性能有重大影响)被考虑进来.芯片表面的温度与瞬时功耗vCEiC成比例.因此,结温是一个二阶现象,它被模拟为一个独立的低频变量.热感应的IM3可以用Volterra模型计算,且它能影响低调制频率处的IM3到高达数百千赫兹.
输出端的IM3不仅是立方非线性效应的和,也是级联的二次方非线性(对总失真有影响)的和.因此,在包络ω2–ω1和二次谐波2ω1处的带外阻抗可以用来优化失真,且通过优化带外阻抗,能将线性提高一些分贝. 由于阻抗,特别是包络阻抗,在一个大范围的调制频率上不可能是常量,IM3的幅度和/或相位不依赖于调制频率,这对许多线性方法来说十分有害.这些记忆效应可以用Volterra模型进行模拟, Volterra模型能够足够精确地预测记忆效应.
带外阻抗和电记忆效应的影响在BJT中要比在MESFET中强.在BJT中,有两个强的,基本上是指数非线性的结构相互之间互相抵消.这种现象对基波和带外阻抗都是十分敏感的,且IM3被后者影响更大.在BJT和MESFET中,很难设计在包络频率处的集电极/漏极阻抗,这是因为需要大的LC时间常量用于能量储存,因此产生了由频率决定的包络阻抗以及记忆效应.这些影响在BJT中更为严重,但是仍需特别观注MESFET中的基带的设计.
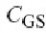
由于,此阻抗很高,并且很明显地倾斜,因此在高调制频
volterra 第四章Volterra模型
率处产生了记忆效应.
动态热效应和TPF在BJT中比在MESFET中更重要.芯片的热阻和包装的热阻十分相似,但是由于在BJT中,电的电路元件对温度更加敏感,因此BJT中产生更多的TPF.在多数情况下,在BJT中需要考虑TPF,然而在MESFET中, 仅当电IM3值非常小时,IM3的相位开始受芯片表面动态温度变化的影响.
整个IM3由许多失真结构组成,其中许多结构之间可以部分地相互抵消.这种跟踪现象取决于匹配阻抗以及非线性系数,它们也轮流地取决于偏置电压.通常在实际中可以观察到,在偏置电压的某些值上,线性会突然地提高.这是由于非线性的抵消引起的,在一些情况下,可以达到很好的线性.不幸的是,跟踪对于阻抗,电压和温度的改变十分敏感,这使得很难对其进行开发.本章所示的Volterra模型仍然为研究这些效应提供了一个系统的分析方法,因此很容易看出跟踪是否是可能的,也容易看出跟踪对哪个参数敏感.对失真结构的仔细研究是成功研究内部抵消结构的关键.
4.7需记住的重点
1.射频功率放大器设计需要精确的失真模拟.
2.通常,仿真模型可以分成两种:动作模型和器件模型.器件模型以预定函数或列表的测量数据为基础.
3.在开发新器件模型中,精确的导数只是一个次要的需求.
4. I-V和Q-V曲线的导数(一直到N阶)必须足够精确,以便用于N阶失真模拟.
5. 使用多项式Volterra模型,导数可以局部地用于实际行为中.
6. Volterra 分析可以给出每个失真机制的响应(或者是解析的,或者是数字的).使得用逐项考虑的方法看待总失真变得可能,这会给设计优化提供许多信息.
7.在射频功率放大器中存在许多部分抵消失真机制,例如,在一个电流驱动的BJT中, gpi和gm非线性间互相抵消.
8.功放设计者对器件内部的非线性控制有限,但是能够影响转移函数,转移函数可以将非线性产生的电流转换为结点电压.
9.由级联的二次非线性引起的IM3在BJT和MESFET放大器中是显著的,特别是在BJT放大器中.
volterra 第四章Volterra模型
10.与MESFET放大器相比,TPF在BJT/HBT中更加重要,这是因为BJT的大多数电路元件是依赖于温度的.
11. Volterra模型是用来确认放大器记忆效应的强大工具.
12.大多数电记忆效应是由低频偏置阻抗引起的.
参考文献

volterra 第四章Volterra模型

volterra 第四章Volterra模型

volterra 第四章Volterra模型

五 : 第四章
我越过电脑与电脑之间的隔道,走到她的座位边,弯腰看着电脑桌面文件夹里她下的图片。
我失声道,这么多啊!你可真会找,怪不得你不知道选那款了。这么多张,你都喜欢吗?
她下了30多张珞丹的短发,每一张都有些许的区别。我见她点头,职业习惯促使我观察了她的脸和五官,略带稚气的鹅蛋型脸加上大大的眼睛顶着双眼皮,突出的小鼻子,稍微翘起弧度的嘴角,然后额头中心点与眼角、眼角与鼻梁、鼻梁与下额尖的距离都差不多,标准的可人儿一个。她留着一头中长发,斜碎的刘海挡住了整个右眼睛,要是剪成珞丹式齐双刘海,沙宣收颈短发,十足又是一个王珞丹的盗版。
见我老盯着她看,又不发表意见,她不太自然的哎了一声。
她说,看出什么来了,我适合剪哪个呀!你倒是说啊!
我赶紧收回目光,不好意思的干笑,用手指着电脑上珞丹图片其中的一张。( 文章阅读网:www.61k.com )
我说,这个适合你,因为你年纪不大,穿的衣服又太过个性,所以现阶段剪这个最搭。
我说完了回到自己的电脑旁。歌曲下完了,我拔出读卡器取下内存卡,然后把读卡器放在了她的显示器边。
女孩说,谢谢哦,我也觉得这一款很适合我的风格。我要回去了,爸妈不在家,我偷偷跑出来的,明天星期六不用上课。
她把下载的东西拉进U盘,取出然后准备下机了。
我微笑着向她招手说再见。
她回头顺便补充了一句,你眼光很好,我去的时候会给你打电话的,拜!
女孩走了,这一片区域只剩下我一个人了。我揉了揉有些发胀的眼睛,又看了会珞丹的后院,总算对她有个大概的了解了。我关上电脑走到收银台结算,再一次敲醒了收银员妹妹,她显得很无奈,我报以歉意。
回到宾馆,管理员正在那钓鱼,我不太忍心吵醒他,可是……
砰砰砰!!!玻璃门被我使劲敲砸着。
我大声道,让我进去。
管理员叔叔头一下磕在了桌子角,嗖的一下站了起来吓了我一跳。他狠狠瞪了我一眼,开了门锁。
躺在床上,我反复展转难眠,拿出手机打开音乐播放器,删除了以前的歌只留下王珞丹的。
“我以为/一个人更容易入睡/我以为/开着灯的夜晚不黑/我以为/冬天的冷/能冻住眼泪/只可惜/一切只是/我以为……”
听着忧伤的《我以为》,有些歌曲意境确实能够刺痛一个人的心,当你寂寞无助的时候感觉全世界只剩下你一个人的时候,来跟我一起细细品味这首《我以为》吧!
“如果爱/牺牲以后/才能永垂/如果心/残缺之前/就懂完美/如果我/还是愿意陪你/看流星下坠/会不会/一秒钟就/千秋万岁/忘了笑/忘了哭/忘了说再会/全都无所谓/无所不为/只是秒针不停时针怎么追/爱你是个错/而我/却不能对……”
珞丹你好,谢谢你陪我度过了今晚难过的夜,我会坚强的面对爱情的逝去,叶梓的离开,我感激叶梓,同样的感动你的《我以为》。
本文标题:第四章-第四章61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1