一 : VerilogHDL的建模方法
Verilog模型可以是实际电路不同级别的抽象,因此有多种不同的建模方法。其中最常用的建模方法有以下三种:
1)门级结构建模
2) 行为描述建模
3) 数据流建模
1.门级结构建模
一个逻辑网络是由许多逻辑门和开关所组成,因此用逻辑门的模型来描述逻辑网络是最直观的。VerilogHDL提供了一些门类型的关键字,可以用于门级结构建模。其中最常用的有8个。
and 与门
nand 与非门
nor 或非门
or 或门
xor 异或门
xnor 异或非门
buf 缓冲器
not 非门
一个模块能在其他模块中被引用,如果已经编制了一个模块,我们可以在另外的模块中引用这个模块,引用的方法与门类型的实例引用非常类似,这样就建立了描述的层次。信号的端口可以通过位置或名称关联,但是不能和混合使用。
例:nand #10nd1(a,data,clock,clear);
实例:
1位全加器(结构描述方式)

1位全加器的逻辑图
module FA_Str(A,B,Cin,Sum,Cout)
input A,B,Cin;
output Cout,Sum;
wire S1,T1,T2,T3;
xor
X1(S1,A,B),
X2(Sum,S1,Cin),
A1(T3,A,B),
A2(T2,B,Cin),
A3(T1,A,Cin);
or
O1(Cout,T1,T2,T3);
endmodule
用两块半加器构成全加器(在一个模块中引用其他模块):
module HA(A,B,S,C) //定义一个半加器
input A,B;
output S,C;
parameter AND_DELAY = 1,XOR_DELAY =2;
assign #XOR_DELAY S = A^B;
assign #AND_DELAY C =A&B;
endmodule
moduleFA(P,Q,Cin,Sum,Cout);
input P,Q,Cin;
Cout Sum,Out;
parameter OR_DELAY = 1;
wire S1,C1,C2;
//两个模块实例语句
HA h1(P,Q,S,C1);//通过位置关联
HA h2(.A(Cin),.S(Sum),.B(S1),.C(C2));//通过端口与信号的名字关联
or # OR_DELAY O1(Cout,C1,C2);
endmodule
门级结构描述如下图所示的D触发器;
moduleflop(data,clock,clear,q,qb);
input data,clock,clear;
output q,qb;
nand #10nd1(a,data,clock,clear),
nd2(b,ndata,clock),
nd4(d,c,b,clear),
nd5(e,c,nclock),
nd6(f,d,nclock),
nd8(qb,q,f,clear);
nand #9 nd3(c,a,d),
nd7(q,e,qb);
not #10 iv1(ndata,data),
iv2(nclock,clock);
endmodule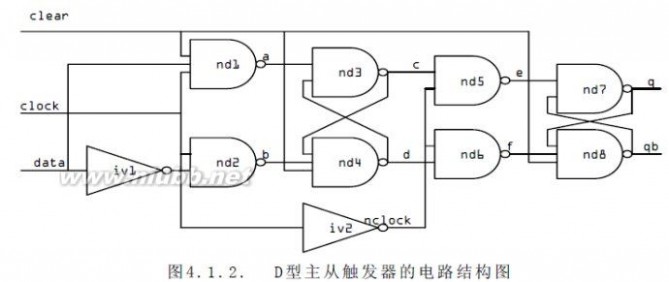
D触发器
用上述的D触发器构成下图的四位寄存器:
modulehardreg(d,clk,clrb,q);
input clk,clrb;
input[3:0] d;
output[3:0] q;
flopf1(d[0(www.61k.com)],clk,clrb,q[0],),
f2(d[1],clk,clrb,q[1],),
f3(d[2],clk,clrb,q[2],),
f4(d[3],clk,clrb,q[3],);
endmodule

四位寄存器
2.Verilog HDL的行为描述建模
行为建模主要用initial和always语句,这些语句相互并行执行,,都在0时刻开始执行,与语句出现的顺序无关。
行为建模的时序控制:(1)时延控制,(2)事件控制。
时延控制:#delayprocedural_statement;其中delay可以是任意表达式而不必是常量。
事件控制:1边沿触发事件控制 2电平敏感事件控制。
边沿触发事件控制:@event procedural_statement;
例如:@(posedgeClock)Count =0;
电平敏感事件控制:wait(condition)
procedural_statement;
例如:wait(Sum > 22)
Sum = 0;
语句块:begin….end;fork…..join;
过程性赋值:阻塞性赋值,非阻塞性赋值。
条件语句:if….else;case;
循环语句:forever,while,repeat,for。
1forever
procedural_statement;//永远执行下去
2repeat(Count)
procedural_statement;//循环Count次
3while(condition)
procedural_statement;
4for(;;)
procedural_statement;
实例:
1位全加器(行为描述方式):
module FA_Seq(A,B,Cin,Cout,Sum);l
input Cin,A,B;
output Cout,Sum;
reg Cout,Sum;
reg T1,T2,T3;
always
@(A or B or Cin)begin
Sum=(A^B)^Cin;
T1=A&Cin;
T2=B&Cin;
T3=A&B;
Cout=(T1 | T2) | T3;
end
endmodule
带异步预置的负边沿触发的D触发器(行为描述方式):
module DFF(Clk,D,Set,Q,Qbar);
input Clk,D,Dset;
outptut Q,Qbar;
reg Q,Qbar;
always
wait(Set == 1)
begin
#3 Q = 1;
#2 Qbar = 0;
wait(Set ==0)
end
always
@(negedge Clk)
begin
if(Set != 1)
begin
#5 Q = D;
#1 = Qbar = ~Q;
end
end
endmodule
3.Verilog HDL的数据流建模
数据流描述的特征:连续赋值,那么连续赋值什么时候执行呢?只要表达式右端的操作数上有事件发生,表达式即被计算。
下面是一些例子:
--------------------------------
wireCout,Cin;
wire[3:0] Sum,A,B;
assign (cout,Sum) = A+B+Cin;
-------------------------------
assign Mux = (S == 0)? A : ‘bz,
Mux= (S == 1)? B : ‘bz,
Mux= (S == 2)? C : ‘bz,
Mux= (S == 3)? D : ‘bz;:
建模实例:
1位全加器(数据流描述)
moduleFA_Df(A<B<Cin,Sum,Cout)
input A,B,Cin;
output Sum,Cout;
assign Sum = A^B^Cin;
assign Cout =(A&Cin)|(B&Cin)|(A&B);
endmodule
主从触发器(数据流描述)
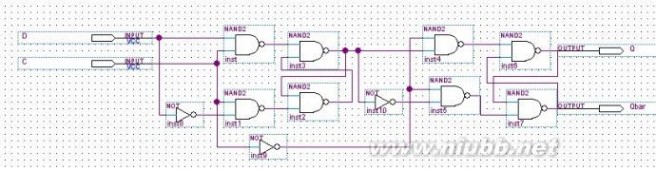
主从触发器逻辑连接图
module MSDFF_DF(D,C,Q,Qbar)
input D,C;
output Q,Qbar;
wire NotC,NotD,NotY,Y,D1,D2,Ybar,Y1,Y2;
assign NotD = ~D;
assign NotC = ~C;
assign NotY = ~Y;
assign D1 =~(D&C);
assign D2 =~(C&NotD);
assign Y =~(D1&Ybar);
assign Ybar =~(Y&D2);
assign Y1 =~(Y&NotC);
assign Y2 =~(NotY&NotC);
assign Q =~(Qbar&Y1);
assign Qbar =~(Y2&NotQ);
endmodule
2-4解码器(数据流描述方式)
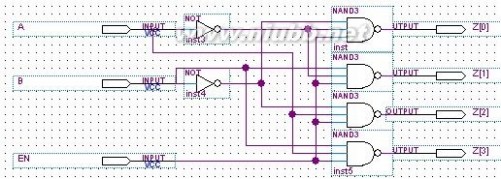
2-4解码器的逻辑图
timescale 1ns/1ns
module Decoder2x4(A,B,EN,Z)
input A,B,EN;
output [0:3] Z;
wire Abar,Bbar;
assign #1 Abar=~A;
assign #1 Bbar=~B;
assign #2Z[0]=~(Abar&Bbar&EN);
assign #2Z[1]=~(Abar&B&EN);
assign #2Z[2]=~(A&Bbar&EN);
assign #2Z[3]=~(A&B&EN);
endmodule
二 : 两种建模方法
2 过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法
2.1 2.2 2.3
过程控制系统建模概念
机理建模方法 测试建模方法
河南科技大学机电工程学院
过程控制系统建模方法
内容
?建立被控对象的数学模型 ?可分为机理法和测试法两大类
河南科技大学机电工程学院
过程控制系统建模方法 ?第一节介绍建模的概念、条件 机理法建模、测试法建模两种方法的基本 思路。
?第二节推导了建模的过程,机理建模的方法。 掌握测试法建模的原理和推导步骤。 ?第三节四种测试建模的方法、特点 测试动态特性的时域法、频域法 统计相关法和最小二乘法。
河南科技大学机电工程学院
过程控制系统建模方法
? 控制系统的设计任务是依据被控对象的数学模 型,按照控制要求来设计控制器。 ? 建立被控对象的数学模型,可分为机理法和测 试法两类。
河南科技大学机电工程学院
过程控制系统建模方法
2.1
过程控制系统建模概念
2.2
2.3
机理建模方法
测试建模方法
河南科技大学机电工程学院
过程控制系统建模方法
2.1.1
2.1.2
建模概念
过程控制系统建模的两个基本方法
4
河南科技大学机电工程学院
过程控制系统建模方法
2.1.1 2.1.2
建模概念
过程控制系统建模的两个基本方法
4
河南科技大学机电工程学院
过程控制系统建模方法
? 三类主要的信息源: 1、要确定明确的输入量与输出量。 ? 通常选一个可控性良好,对输出量影响最大的 一个输入信号作为输入量,其余的输入信号则 为干扰量。
河南科技大学机电工程学院
过程控制系统建模方法
2、要有先验知识 ?在建模中,被控对象内部所进行的物理、化学 过程符合已经发现的许多定理、原理及模型。 ?在建模中必须掌握建模对象所要用到的先验知 识。
3、试验数据 ?过程的信息能通过对对象的试验与测量而获得。
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法
?被控对象数学模型的要求:要求它准确可靠。 在线运用的数学模型要求实时性。 ?在建立数学模型时,要抓住主要因素,忽略次要 因素,需要做很多近似处理 ?如:线性化、分布参数系统和模型降阶处理等。 ?用于控制的数学模型并不要求非常准确。 ?闭环控制本身具有一定的鲁棒性,模型的误差 可以视为干扰,闭环控制在某种程度上具有自动 消除干扰影响的能力。
河南科技大学机电工程学院
过程控制系统建模方法
2.1.1 2.1.2
建模概念 过程控制系统建模的两个基本方法
4
河南科技大学机电工程学院
过程控制系统建模
方法 1、机理法建模
?根据生产过程中实际发生的变化机理,写出各种 有关的平衡方程
?如:物质平衡方程;能量平衡方程;动量平衡方程 以及反映流体流动、传热、传质、化学反应等基本 规律的运动方程,物性参数方程和某些设备的特性 方程等,从中获得所需的数学模型。
河南科技大学机电工程学院
过程控制系统建模方法 ? 用机理法建模的首要条件是生产过程的机理必 须为人们充分掌握,可以比较确切的加以数学 描述。 ? 模型应该尽量简单,保证达到合理的精度。 ? 用机理法建模时,出现模型中某些参数难以确 定的情况或用机理法建模太烦琐。 ? 可以用测试的方法来建模。
河南科技大学机电工程学院
过程控制系统建模方法
2、测试法建模
?根据工业过程的输入和输出的实测数据进行数学 处理后得到的模型。
?特点是把被研究的工业过程视为一个黑匣子,完 全从外特性上测试和描述它的动态性质,不需要深 入掌握其内部机理。
河南科技大学机电工程学院
过程控制系统建模方法 ? 为了获得动态特性,必须使被研究的过程处于 被激励的状态,施加一个阶跃扰动或脉冲扰动 等。 ? 用测试法建模一般比用机理法建模要简单和省 力, ? 如果两者都能达到同样的目的,一般都采用测 试法建模。
河南科技大学机电工程学院
过程控制系统建模方法
?测试法建模又可分为经典辨识法和现代辨识法 两大类。 ?经典辨识法只需对少量的测试数据进行简单的 数学处理, ?现代辨识法可以消除测试数据中的偶然性误差 即噪声的影响,需要处理大量的测试数据。
河南科技大学机电工程学院
过程控制系统建模方法
2.1
过程控制系统建模概念
2.2 机理建模方法
2.3 测试建模方法
河南科技大学机电工程学院
过程控制系统建模方法
1、单容水槽 ?水流入量Q1由调节阀开度μ加以控制,流出量 Q0则由用户根据需要通过负载阀来改变。 ?被调量为水位h,它反映水的流入与流出之间 的平衡关系。 ?分析水位在调节阀开度扰动下的动态特性。
河南科技大学机电工程学院
过程控制系统建模方法
1—控制阀门 2—水槽 3—负载阀(液阻R)
单容水槽
河南科技大学机电工程学院
过程控制系统建模方法
?各量定义如下: ? Qi——输入水流量的稳态值( m3/s); ?ΔQi ——输入水流量的增量(m3 /s); ?Qo ——输出水流量的稳态值(m3 /s); ?ΔQo ——输出水流量的增量(m3 /s); ?h——液位的高度(m); ?ho ——液位的稳态值(m); ?Δh——液位的增量(m); ?μ——调节阀的开度( m2);
河南科技大学机电工程学院
过程控制系统建模方法
? 设A为液槽横截面积(m2),R为流出侧负载阀 门的液阻(s/m2 )。根据物料平衡关系,在正 常工作状态下,初始时刻处于平衡状态Qi=Qo, h=ho,当进水阀开度发生阶跃变化Δμ时,液 位发生变化。在流出侧负载阀开度不变的情况 下,液位的变化将使流出量改变。 ? 流入量与流出量之差等于液槽液体贮存量的变 化率,即:
河南科技大学机电工程学院
过程控制系统建模方法
dV Q ? Δ Δ Qi-Δ -Δ =0 = =A dt
d?h =A dt
?Δ Qi 是由控制阀开度变化Δμ引起的,当阀前 后压差不变时,ΔQi与Δμ成正比关系,即 ΔQi= K ? Δμ
河南科技大学机电工程学院
过程控制系统建模方法
?K ? 为阀门流量系数(m/s)。
? 流出量与液位高度的关系为
Q = A0
2gh =
K
h
?(2—3)
河南科技大学机电工程学院
过程控制系统建模方法
?式(2—3)是一个非线性关系,如图 2.3所示,在平衡点( h0、Q0)附近进 行线性化,得 ?h R = ?Q (2—4)
0
河南科技大学机电工程学院
过程控制系统建模方法
液位与流出量的关系
河南科技大学机电工程学院
过程控制系统建模方法
?将式(2—4)、(2—2)代入式(2—1),可得 ? d?h RA + Δh = K ? RΔμ (2-5) dt ?
河南科技大学机电工程学院
过程控制系统建模方法 ? 令 T = RA (s), K = K ? R (1/m), 则上式可写为
d ?h T dt + Δh = KΔμ
(2-6)
? 可得液位变化时控制阀开度改变量的传递函数 为 K ?H ( s ) G(s) = = (2-7) ?U ( s ) TS ? 1
河南科技大学机电工程学院
过程控制系统建模方法
2、电加热炉
?被控参数为炉内温度T,控制量为电热丝两端电压u ?加热丝质量为M,比热为C,传热系数为H,传热 面积为A,未加温前炉内温度为T0,加温后的温度为T
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法
?根据热力学知识,有 ? d (T ? T0 ) MC + HA(T-T0)=Qi dt ?
(2-8)
河南科技大学机电工程学院
过程控制系统建模方法
?式中: Qi 为单位时间内电热丝产生的热 量。 ?Qi 与外加电压u的平方成比例,故 Qi 与u是非线性关系。 ?在平衡点( Qo 、U0 )附近进行线性 化,得 ? ?Qi ?K u = ?u ?
河南科技大学机电工程学院
过程控制系统建模方法
?于是可得式(2-8)对应的增量微分方程 d?T MC + HAΔT = K uΔu (2-9) dt ? Ku MC 令 τ= K= 则上式可写为 HA HA ?
?
d?T Τ dt
+ ΔT = KΔu
(2-10)
河南科技大学机电工程学院
过程控制系统建模方法 可得炉内温度变化量对控制电压变化量之间的传 递函数为
G(s) =
?T ( s ) = ?u ( s )
K ?s ? 1
(2-11)
河南科技大学机电工程学院
过程控制系统建模方法 3、压力对象
压力对象如图所示.
河南科
技大学机电工程学院
过程控制系统建模方法
? ? d?p0 RC +Δ dt ? ? ?
p0
=Δ
pi
河南科技大学机电工程学院
? ?可得容器压力变化量与进气压力变化量 之间的传递函数如下: ? 1 ?p0 (s) G(s)= = ?pi (s) RCS ? 1 ? ?
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法 ? 单容被控对象动态特性都是一阶惯性环节
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法 具有纯延迟的单容对象特性 ? 有一储水槽调节阀1距水槽有一段较长的距离。调 节阀1开度变化所引起的流入量变化 ΔQi,需要经 过一段传输时间 T0,才能对水槽液位产生影响, T0 是纯延迟时间。
河南科技大学机电工程学院
过程控制系统建模方法 ?纯延迟现象产生的原因是由于扰动发生的地点与 测定被控参数位臵有一定距离。 ?
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法
d ?h T + Δh = KΔμ dt
?有纯延迟的单容对象的微分方程为
d?h T dt
+Δh = KΔu(t -
?0)
(2-17)
河南科技大学机电工程学院
过程控制系统建模方法
对应的传递函数为 G(s)=
?H ( s ) K ?? e = Ts ? 1 ?U ( s )
0s
(2-18)
?? 0 s
与式(2-7)相比多了延迟因子 e
。
河南科技大学机电工程学院
过程控制系统建模方法 无自平衡能力的单容对象特性 ?用惯性环节描述的单容对象,在被控量受到扰 动后,原来的平衡关系遭到破坏,但随着被调量 的变化不平衡越来越小,被调量能够自动地稳定 在新的平衡点上,这种特性称为自平衡。 ?具有自平衡特性的被控对象称为自平衡过程。 ?这是一种稳定的过程。
河南科技大学机电工程学院
过程控制系统建模方法 ? 另有一些被控对象,其流出端是用容积式的计 量泵排出恒定的流量Q,其值与液位的高低无 关。 ? 当流入端的流量发生阶跃扰动时,原来平衡关 系被破坏,液位发生变化。 ? 由于流出端流量保持不变,则液位或者上升, 直至水溢出液槽;或者下降,直到液槽里的水 被抽完为止。
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法
?当这种被调量的平衡关系破坏后,不平 衡不因被调量的变化而改变,被调量而 以固定的速度一直变化下去而不会自动 地在新的水平上恢复平衡。这种现象不 具有自平衡特性,称为无自平衡过程。 这种过程是临界稳定的,它需要很长时 间,被调量才会有很大的变化。
河南科技大学机电工程学院
过程控制系统建模方法
?还有一类不稳定的过程,原来的平衡一旦被破坏 后,被调量在很短的时间内就发生很大的变化。
河南科技大学机电工程学院
过程控制系统建模方法
?对于无自平衡能力的单容对象其动态方 程为
d?h A =Δ dt
Qi
=
K u? u
(2—19)
A——液槽截面积。
河南科技大学机电工程学院
过程控制系统建模方法
?对于无自平衡能力的单容对象其动态方 程为
d?h A =Δ dt
Qi
=
K u? u
(2—19)
A——液槽截面积。
河南科技大学机电工程学院
过程控制系统建模方法 ? 对式(2-20)求解可得
?h =
??u
·
t=
= ? 对应的传递函数为
Ta
A = Ku
1 为响应时间。其 ?
?u t Ta
1 1 ?H ( s ) G(S)= ?U ( s ) = T (2-22) s a 这是一个积分环节,响应曲线如图所示。
河南科技大学机电工程学院
过程控制系统建模方法
?无自平衡能力单容对象阶跃响应曲线
河南科技大学机电工程学院
过程控制系统建模方法 多容对象的动态特性 ? 具有两个水槽,有两个可以储水的容器,为双容 对象。
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法 1、具有自平衡能力的双容对象
? 两个串联对象的模型,在流入端,阀门开度有 微小扰动的情况下,被控参数 ?h2 的动态方程可由几个关系式导出。
河南科技大学机电工程学院
过程控制系统建模方法
?Q1 -
?Q2 =
C2
d?h2 dt
?Q2
?h2 = R2
?h1 R1
?Q1 =
?Qi -
?Q1
d ? h 1 C = 1 dt
?Qi = K u ? u
河南科技大学机电工程学院
过程控制系统建模方法
? 消去中间变量可得
T1 T
+
d ? h2 2 dt 2
2
+ ( T1 +T
2
?h2
=K
?u
d?h2 ) dt
河南科技大学机电工程学院
过程控制系统建模方法
C1、C2——两液槽的容量系数; R1、R2——两液槽的出水端的阻力; T1= R1C1——第一个容器的时间常数; T2=R2C2——第二个容器的时间常数; K= KuR2——双容对象的放大系数。
河南科技大学机电工程学院
过程控制系统建模方法
其传递函数为
?H 2 ( s ) G(s) = ?U ( s )
=
K T1T2 s 2 ? (T1 ? T2 ) s ? 1
河南科技大学机电工程学院
过程控制系统建模方法
?若双容对象调节阀 1 开度变化所引起的流入量 还存在纯延迟,则其传递函数可推导为
G(s)=
?H 2 ( s ) ?U ( s )
=
K ?? 0 s e T1T2 s 2 ? (T1 ? T2 ) s ? 1
河南科技大学机电工程学院
过程控制系统建模方法
?h1
?h1
河南科技大学机电工程学院
过程控制系统建模方法
2、具有自平衡能力的多容对象
有 n 个相互独立的多容对象的时间常数为 T1 、 T2….Tn,总放大系数为K,则传递函数为 G(s)=
K (T1 s ? 1)(T2 s ? 1) ?(Tn s ? 1)
河南科技大学机电工程学院
过程
控制系统建模方法
? 若T1=T2=……=Tn=T
则
K G(s)= (Ts ? 1) n
? 若还有纯延迟,则
K ?? 0 s G(s)= n e (Ts ? 1)
河南科技大学机电工程学院
过程控制系统建模方法
3.无自平衡能力的双容对象
?图示的无自平衡能力的双容对象是一个有自平 衡能力的单容对象和一个无自平衡能力的单容对 象的串联。
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法
? u 阶跃扰动 ?当流入端阀门在t0时刻发生 时,由于多了一个中间液糟,作为 ?h被控 2 参数,并不能立即以最大速度变化, 对 ? h2 ,可 扰动的响应有一定的惯性, =0 ?Q2 得其对象的动态方程为
河南科技大学机电工程学院
过程控制系统建模方法
R 1C 1
d ? h2 2 dt
2
d?h2 + dt
Ku = ?u C2
河南科技大学机电工程学院
过程控制系统建模方法 令 T= R1C1 则得 ,
, Ta = C2 / Ku
T
d 2 ? h2 dt 2
d?h2 + dt
1 ?u = Ta
其对应的传递函数为
1 1 ? G(s)= Ts ? 1 Ta s
河南科技大学机电工程学院
过程控制系统建模方法 有纯延迟的情况则
G(s)=
1 1 ? Ts ? 1 Ta s
e
?? 0 s
河南科技大学机电工程学院
过程控制系统建模方法
?无自平衡能力双容对象的阶跃响应曲线
河南科技大学机电工程学院
过程控制系统建模方法 4、相互作用的双容对象 ? 前述双容对象,后一容器液位变化对前一容器 液位无影响。 ? 有一种双容水槽,两个水槽中,一水槽液位的 高低会影响另一水槽液位变化,两者之间有相 互作用,结果会改变水槽的等效时间常数。
河南科技大学机电工程学院
过程控制系统建模方法
?具有相互作用的双容模型 ?
河南科技大学机电工程学院
过程控制系统建模方法
?Qi 原来平衡时, ? 设被控参数为 ?Q0 输入扰动为 Q0=Q1=Qi,H10=h20 ; ? 当输入有扰动 ?Qi 后,会产生?h1 , ?h2 , ?Q0 ? 其之间关系为 ?
河南科技大学机电工程学院
过程控制系统建模方法
?h1 ? ?h2 ? ?Q1 R1
d?h1 ?Qi ? ?Q1 ? C1 dt
?h2 ?Q2 ? R2
d?h2 ?Q1 ? ?Q0 ? C 2 dt
河南科技大学机电工程学院
过程控制系统建模方法
可得对应的传递函数为
?Q0 (s) 1 ? 2 ?Qi (s) R1C1 R2 C2 s ? ( R1C1 ? R2 C2 ? R2 C1 )s ? 1
河南科技大学机电工程学院
过程控制系统建模方法 若以Δh2为被控参数,则
?H 2 (s) R2 ? ?Qi (s) R1C1 R2 C2 s 2 ? ( R1C1 ? R2 C2 ? R2 C1 )s ? 1
河南科技大学机电工程学院
过程控制系统建模方法
2.1
过程控制系统建模概念
2.2 机理建模方法
2.3 测试建模方法
河南科技大学机电工程学院
过程控制系统建模方法
?对于某些生产过程的机理,人们往往还未充分 掌握,有
时也会出现模型中有些参数难以确定的 情况。这时就需要用过程辩识方法把数学模型估 计出来。
河南科技大学机电工程学院
过程控制系统建模方法
对象特性的实验测定方法
? 工业对象通常是由高阶非线性微分方程描述的 复杂对象,对这些方程式较难求解。
河南科技大学机电工程学院
过程控制系统建模方法 ?采用机理法在推导和估算时,常用一些假设和近 似。数学模型希望通过实验测定来验证。 ?在无法采用机理法得到数学模型的情况下,只有 依靠实验和测试方法来取得。
河南科技大学机电工程学院
过程控制系统建模方法 ? 过程的动态特性,当它处于变动状态下才会表 现出来,在稳定状态下是表现不出来的。为了 获得动态特性,必须使被研究的过程处于被激 励的状态 ? 根据加入的激励信号和结果的分析方法不同, 测试对象动态特性的实验方法也不同,主要以 下几种:
河南科技大学机电工程学院
过程控制系统建模方法
(1)测定动态特性的时域方法 ?对被控对象施加阶跃输入,测绘出对象输出量 随时间变化的响应曲线,或施加脉冲输入测绘出 输出的脉冲响应曲线。 ?由响应曲线的结果分析,确定出被控对象的传 递函数。 ?该方法测试设备简单,测试工作量小、应用广 泛,缺点是测试精度不高。
河南科技大学机电工程学院
过程控制系统建模方法
(2)测定动态特性的频域方法 ? 对被控对象施加不同频率的正弦波,测出输入 量与输出量的幅值比和相位差,获得对象的频 率特性,来确定被控对象的传递函数。
河南科技大学机电工程学院
过程控制系统建模方法 (3)测定动态特性的统计相关法 ?对被控对象施加某种随机信号或直接利用对象 输入端本身存在的随机噪音进行观察和记录, ?可以在生产过程正常运行状态下进行,在线辨 识,精度也较高。 ?统计相关法要求积累大量数据,并要用相关仪 和计算机对这些数据进行计算和处理。 ?
河南科技大学机电工程学院
过程控制系统建模方法
? 三种方法测试的动态特性,表现形式是以时间 或频率为自变量的实验曲线,是非参数模型。 ? 建立数学模型的方法称为非参数模型辨识方法 或称经典的辨识方法。
河南科技大学机电工程学院
过程控制系统建模方法 非参数模型:阶跃响应R(t)频率响应G(jw)经过适当 的数学处理可转变成参数模型:传递函数的形式。
河南科技大学机电工程学院
过程控制系统建模方法 ?根据不同的基本原理又可分为 ?最小二乘法; ?梯度校正法; ?极大似然法三种类型。
河南科技大学机电工程学院
过程控制系统建
模方法 ? 最小二乘法是利用最小二乘原理,通过极小化广 义误差的平方和函数来确定模型的参数。
河南科技大学机电工程学院
过程控制系统建模方法 测定动态特性的时域法 ?在被控对象上,人为地加非周期信号后,测定 被控对象的响应曲线,然后再根据响应曲线,求 出被控对象的传递函数。
河南科技大学机电工程学院
过程控制系统建模方法
?测试响应曲线的框图
河南科技大学机电工程学院
过程控制系统建模方法 ?1—被测对象 ?2—变换器 ?3—记录仪
河南科技大学机电工程学院
过程控制系统建模方法 1、输入信号选择及实验注意事项 ? 对象的阶跃响应曲线比较直观地反映对象的动 态特性,它是直接来自原始的记录曲线,无需 转换,实验也比较简单,从响应曲线中也易于 直接求出其对应的传递函数。 ? 阶跃输入信号是时域法首选的输入信号。
河南科技大学机电工程学院
过程控制系统建模方法
?有时生产现场运行条件受到限制,不允许被控 对象的被控参数有较大幅度变化,无法测出一条 完整的阶跃响应曲线,可改用矩形脉冲作为输入 信号,得到脉冲响应后, 再将其换成一条阶跃 响应曲线。
河南科技大学机电工程学院
过程控制系统建模方法 ? 测试办法及曲线转换方法: ? 首先在对象上加一阶跃扰动,待被控参数继续 上升(或下降)到将要超过允许变化范围时, 立即去掉扰动,即将调节阀恢复到原来的位臵 上,变成了矩形脉冲扰动形式。
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法 在图中可看出:
u(t ) ? u1 (t ) ? u 2 (t ) u 2 (t ) ? ?u1 (t ? ?t )
设:U1(t). U2(t) 和y2(t) 。
作用下的阶跃响应曲线为y1(t)
河南科技大学机电工程学院
过程控制系统建模方法 ?则脉冲响应曲线为
y(t ) ? y1 (t ) ? y2 (t ) ? y1 (t ) ? y1 (t ? ?t )
即
y1 (t ) ? y(t ) ? y1 (t ? ?t )
(2—35)
式(2—35)就是由矩形脉冲响应曲线y(t),转换 为阶跃响应曲线的根据。
河南科技大学机电工程学院
过程控制系统建模方法
具体作法如下: 将时间轴按 ? t 分成 n 等份,在 0~t0+ ?t 区间,阶跃响应曲线与矩形脉冲响应 曲线重合。 即 y1(t)=y(t) 0 < t ? t 0 ? ?t (2—36)
河南科技大学机电工程学院
过程控制系统建模方法 在
t 0 ? ?t ? t ? t 0 ? 2?t
区间内
y1 (t ) ? y(t ) ? y1 (t ? ?t 0 )
(2—37)
依此类推,最后得到完整的阶跃响应曲线。
河南科技大学机电工程学院
过程控制系统建模方法 实验过程中应注意一些问题 (1)采取一切措施防止其它干扰的发生,否则将影 响实验结果
。 ? 为防止其它干扰影响,同一阶跃响应曲线应重复 测试两三次,以便进行比较,从中剔除某些明显 的偶然误差,并求出其中合理部分的平均值。
河南科技大学机电工程学院
过程控制系统建模方法
(2)在对象的同一平衡工况下,加上一个反向的阶 跃信号,测出对象的响应特性,与正方向的响应 特性进行比较,以检验对象的非线性特性。
河南科技大学机电工程学院
过程控制系统建模方法 (3)测试应进行到被控参数接近它的稳态值或至少 也要测试到被控参数的变化速度达到最大值之 后。 (4)一般应在被控对象最小、最大及平均负荷下重 复测试n条响应曲线进行对比。 (5)要注意被测量起始状态测量的精度和加阶跃信 号的计时起点,这对计算对象延迟的大小和传 递函数确定的准确性有关。
河南科技大学机电工程学院
过程控制系统建模方法 2、实验结果的数据处理 ?如何将实验所获得的各种不同响应曲线进行处 理,以便用一些简单的典型微分方程或传递函数 来近似表达,既适合工程应用,又有足够的精度, 这就是数据处理要解决的问题。
河南科技大学机电工程学院
过程控制系统建模方法
? 用测试法建立被控对象的数学模型,首要的问 题就是选定模型的结构。 ? 典型的工业过程的传递函数可以取为各种形式, 常见形式如下:
河南科技大学机电工程学院
过程控制系统建模方法
一阶惯性环节加纯延迟 G(s)=
??s
Ke Ts ? 1
??s
二阶惯性环节加纯延迟
Ke G(s)= (T1 s ? 1)(T2 s ? 1)
河南科技大学机电工程学院
过程控制系统建模方法
n个相同极点的n阶惯性环节加纯延迟
G(s)=
Ke n (Ts ? 1)
??s
河南科技大学机电工程学院
过程控制系统建模方法
上述几个公式只适用于自平衡过程,对于无自平 衡过程,其传递函数中应含有一个积分环节,形 式如下:
G(s)=
1 ??s e T as
1 ??s e G(s)= Ta s(Ts ? 1)
河南科技大学机电工程学院
过程控制系统建模方法
? 根据阶跃响应曲线,如何来选择上面哪一种传 递函数与其对应,这与测试者对被控对象的验 前知识掌握的多少和本人的经验有关。 ? 一般来说,可将测试的阶跃响应曲线与标准的 一阶、二阶阶跃响应曲线比较,来确定其相近 曲线对应的传递函数形式作为其数据处理的模 型。
河南科技大学机电工程学院
过程控制系统建模方法
?对同一条响应曲线,用低阶传递函数拟合,数 据处理简单,计算量也小,但准确程度较低。 ?用高阶传递函数来拟合,则数据处理麻烦,计 算量大,但拟合精度也较高。
河南科技大学机电工程学院
过程控制系统建模方法
闭环控制尤其是最常用
的PID控制并不要求非常 准确的被控对象。在满足精度要求的情况下, 尽量使用低阶传递函数来拟合,一些工业过程 对象采用一、二阶传递函数拟合为多。 用作图法确定参数T、τ
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法
设阶跃输入幅值为Δu,则K可按下式求取 K=
y ( ? ) ? y ( 0) ?u
(2-43)
河南科技大学机电工程学院
过程控制系统建模方法
?T、τ可用作图法确定,即在拐点p处作切 线,它与时间轴交于 A 点,与曲线的稳态 值渐近线交于 B 点。如图 2.17 所示,图中 的τ、T即式(2-38)中的τ、T值。
河南科技大学机电工程学院
过程控制系统建模方法
作图法十分简单,而且实践表明它可以成功地应 用于PID调节器的参数整定,故应用的也较广 泛。
河南科技大学机电工程学院
过程控制系统建模方法 用两点法求式(2-38)的K、T、τ参数。 上述中用作图法求取参数不够准确,这里所用两 点法,即利用阶跃响应曲线 y( t)上的两点数据去计算 T和 τ值。而 K值仍按 式(2-43)计算。 首先需要把y(t)转换成它的无量纲形 式 y ? (t ) , 即
y (t ) y (t ) ? y (? )
?
河南科技大学机电工程学院
过程控制系统建模方法
其中y(∞)为y(t)的稳态值。 与一阶惯性环节加纯延迟相对应的阶跃响 应无量纲形式为
0 ? ? ? t ?? y (t ) ? ? 1 ? exp( ? ) ? T ?
t ?? t ??
(2-44)
河南科技大学机电工程学院
过程控制系统建模方法
为解出上式的T、τ须选择两个时刻t1和, t 2 ? t1 ,? ? t2,其中 从测试结果中可读出 和 ? 并写出联立方程 ? y (t 2 ) y (t1 ) (2-45) t1 ? ? ? ?
? y (t1 ) ? 1 ? exp(? T ) ? t2 ? ? ? ? y (t 2 ) ? 1 ? exp(? ) T ?
河南科技大学机电工程学院
过程控制系统建模方法 由式(2-45)可解出
t 2 ? t1 ? T? ? ? ? ln[ 1 ? y ( t )] ? ln[ 1 ? y (t 2 )] ? 1 ? ? ? ?? ? t 2 ln[1 ? y (t1 )] ? t1 ln[1 ? y (t 2 )] ? ? ? ln[1 ? y (t1 )] ? ln[1 ? y (t 2 )] ?
(2-46)
河南科技大学机电工程学院
过程控制系统建模方法 为了计算方便,可取,
y ? (t1 ) ? 0.39; y ? (t 2 ) ? 0.63
则可得
?T ? 2(t 2 ? t1 ) ? ? ? ? 2t1 ? t 2
(2-47)
河南科技大学机电工程学院
过程控制系统建模方法 计算出 T 、 τ ,准确与否还可另取两个时刻进行 校验。即
?t 3 ? 0.8T ? ? ? ? t 4 ? 2T ? ?
y (t 3 ) ? 0.55 ? y (t 4 ) ? 0.87
(2-48)
?
河南科技大学机电工程学院
过程控制系统建模方法 2 . 3 用二阶惯性环节加纯延迟拟合图 2-16 曲线, 求K、τ的方法。 增益K值仍可按式2-43
计算。时间纯延迟τ可根据 阶跃响应曲线脱离起始的毫无反应的阶段开始出 现变化的时刻来确定,见图2.18。然后截去纯延 迟部分,并化为无量纲形式的阶跃响应 。 ? y t) 图2.18 (根据阶跃响应曲线上两个点的数据确定 T1 和 T2
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法 式(2-39)截去纯延迟并化为无量纲形式后,所 对应的传递函数形式为
G(s)=
1 (T1 s ? 1)(T2 s ? 1)
T1 ? T2
(2-49)
河南科技大学机电工程学院
过程控制系统建模方法
与上式对应的阶跃响应为 t ? ? y (t ) = 1 ? T1 e T ? T2
T1 ? T2
1
T2 ? T1
e
?
t T2
或
1 - y (t )
?
T1 = T ?T e 1 2
?
t T1
T2 ? e T2 ? T1
?
t T2
(2-50)
河南科技大学机电工程学院
过程控制系统建模方法
根据式( 2-50 )可以利用响应曲线图 2.18 上的 ? 两个数据点[ ]) t1 , y (t1 ? 和[ t 2 , y (t 2 ) ]确定参数T1 T2。 ? 一般 y (t ) 可取分别为0.4和0.8,再从曲线上定出 t1和,t2,如图2-17所示,即可得如下联立方程。
河南科技大学机电工程学院
过程控制系统建模方法
t t1 ? 1 ? ? T T2 T1 T2 1 e ? e ? 0.6 ? ?T1 ? T2 T1 ? T2 ? t2 t2 ? ? ? T1 e T1 ? T2 e T2 ? 0.2 ?T ? T T1 ? T2 2 ? 1
河南科技大学机电工程学院
过程控制系统建模方法
将 y (t )所取两点查得t1和t2代入式(2-51) 便可得到所需的T1 T2。 为求解方便,式(2-51)也可以近似表示 如下: 1 (2-52) T ?T ? (t ? t )
1 2
?
2.16
1
2
T1T2 t1 ? (1.74 ? 0.55) 2 t2 (T1 ? T2 )
河南科技大学机电工程学院
过程控制系统建模方法
在固定选取y (t )分别为0.4和0.8后,其对应的 t1和t2能够反映出其应该对应于式(2-40) 的传递函数的阶次,其关系见表2.1。 表2.1 高阶惯性对象1/ 中阶数n与 t1 / t 2比值的关系
(Ts ? 1)
n
?
河南科技大学机电工程学院
过程控制系统建模方法
n 1 2 3 4 5 6 7
t1/ t2 0.32 0.46 0.53 0.58 0.62 0.65 0.67
n 8 9 10 11 12 13 14
t1/ t2 0.658
0.71
0.735
0.75
河南科技大学机电工程学院
过程控制系统建模方法
表中t1和t2应是 y (t ) 取0.4和0.8所对应的 t1 、 t2 ;式( 2-40 )中的时间常数 T 可由 下式求得
?
t1 ? t 2 nT ? 2.16
(2-54)
河南科技大学机电工程学院
过程控制系统建模方法 ?综上所述,用式(2-39)或式(2-40)拟合测 试响应曲线,确定其参数的步骤如下:
河南科技大学机电工程学院
过程控制系统建模方法
(1) 将响应曲线化为无延迟无量纲的 ? y (t ) 标准形式, (2) 求取 t1 / t 2 分别为0.4和0.8所对应 的T1和t2,根据 的值确定选择n。 t1 0 . 32 ? ? 0.46 若 ,则可选用式(2t2 39),其中T1 T2可按式(2-51)或
式 (2-52)、(2-53)求得。
河南科技大学机电工程学院
过程控制系统建模方法
t1 t2
(4)若 不在(3)的范围,则根据表21 找其相近的数据对应的 n 值选用式( 240),式中T的值按式(2-54)求得。
河南科技大学机电工程学院
过程控制系统建模方法
t1 不在(3)的范围,则根据表2t2
(4)若 1 找其相近的数据对应的 n 值选用式( 240),式中T的值按式(2-54)求得。
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法
( 1 ) 用式( 2-41 )来近似图 2.19 的响应 曲线,公式重写如下: G(s)=
1 ??s e Ta s
作响应曲线稳态上升部分过拐点 A 的切线 交于时间轴于t2,切线与时间轴夹角为θ, 如图2.19所示。
河南科技大学机电工程学院
过程控制系统建模方法 从图2.19看曲线稳态上升部分可看作一条过原点 的直线,向右平移 t2距离,即图中曲线稳态部分 可看作是经过纯延迟 t2后的一条积分曲线。因此 式(2-41)中
?u Ta ? tg?
τ=t2
式中Δu——阶跃输入幅值。
河南科技大学机电工程学院
过程控制系统建模方法
(2)用式(2-42)来近似图2.19响应曲线、 公式重写如下:
e G(s)= Ta s(Ts ? 1)
从图2.19可见在0到t1时间y(t)= 0是纯延 迟,故取τ= t1。
??s
河南科技大学机电工程学院
过程控制系统建模方法
在曲线稳态之后是积分环节作用为主,故
?u Ta ? tg? 而曲线由 t1 至 A 之间其惯性环节作用为 主,故T= t2 -t1
河南科技大学机电工程学院
过程控制系统建模方法 2.3.3 测定动态特性的频域法 2.3.4 最小二乘法 被控对象的动态特性可用频率特性来描述
y ( j? ) G ( jw) ? ? G ( j? ) ?G ( j? ) u ( j? )
与传递函数及微分方程一样,也表征系统的运动 规律。
河南科技大学机电工程学院
过程控制系统建模方法 频率特性表达式可以通过频率特性测试的 方法来得到。 在所研究对象的输入端加入某个频率 的正弦波信号,同时记录输入和输出的稳定振荡 波形,可测得该被控对象的频率特性。
河南科技大学机电工程学院
过程控制系统建模方法
信号发生器
x
调节阀
对象
测量仪
y
变换器 记 录 仪
河南科技大学机电工程学院
过程控制系统建模方法
用正弦波的输入信号测定对象频率特性的 优点在于,能直接从记录曲线上求得频率特性
河南科技大学机电工程学院
过程控制系统建模方法
测量装臵应能滤出与激励频率一致的有用 信号,并显示其响应幅值,相对于激励信号的 相角,给出其同相分量及正交分量,画出在该 测量点上系统响应的奈氏图。
河南科技大学机电工程学院
过程控制系统建
模方法
原理:激励输入信号经波形变换可得 到幅值恒定的正余弦参考信号。 把参考信号与被测信号进行相关处理(即相乘 和平均);所得常值(直流)部分保存了被测信 号同频分量(基波)的幅值和相角信息。
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法
图中: A——被测对象响应 G( j? ) 的同相分量; B——被测对象响应 G( j? ) 的正交分量; R——输出的基波幅值; θ——对象输入与输出的相位差; 1gR——输出基波幅值的对数值。
河南科技大学机电工程学院
过程控制系统建模方法 2.3.4 测定动态特性的统计相关法 在被测对象上加随机信号x(t),测量被控参 数y(t),计算出自相关函数 Rxx (? ) 和x(t) 与y(t)的互相关函数 Rxy (? ) ,求出脉冲响应 g ( t ),然后转换成阶跃响应,最后得到 G(s) 。
河南科技大学机电工程学院
过程控制系统建模方法
抗干扰性强,在获得同样的信息量时, 对系统正常运行的干扰程度比其它的方法低。对 反应慢、过渡时间长的系统更为有效。
河南科技大学机电工程学院
过程控制系统建模方法 1、平稳随机过程的概念
(1)随机信号:设信号都是随时间随机变化的, 称为随机信号. 它们的集合称为随机过程。
河南科技大学机电工程学院
过程控制系统建模方法 (2)平均值、均方值
1 k x1 (T1 ) ? ? xi (T1 ) k i ?1
河南科技大学机电工程学院
过程控制系统建模方法
均方值
k 1 2 x1 (T1 ) ? ? x 2 i (T1 ) k i ?1
河南科技大学机电工程学院
过程控制系统建模方法 ( 3 )平稳随机过程:随机过程是一个时间函 数,它的每一个时刻的数值都可看作为一个随 机变量。一个随机过程,它的统计特性在各个 时刻都不变,称之为平稳随机过程。
? x (T1 ) ? x (T2 ) ? x (T3 ) ? ? ? 2 2 2 x ( T ) ? x ( T ) ? x (T3 ) ? ? 1 2 ?
河南科技大学机电工程学院
过程控制系统建模方法
(4)自相关函数: (5)互相关函数: (6)功率谱密度; (7) 白噪声:
河南科技大学机电工程学院
过程控制系统建模方法
S xx (? ) 在所考虑的频率范围内其谱密度 的幅值是恒定的,就可以认为其是一个白噪声。 白噪声只是理论上的抽象,实际上是不存在的。
河南科技大学机电工程学院
过程控制系统建模方法 2、统计相关法的基本原理 一个线性对象的输入函数x(t)是平稳的随机 过程,相应的输出y(t)也是平稳的随机过程。 设g(t)为对象的脉冲响应函数,相关法的思想 就是:从输入x(t)与输出y(t)的互相关函 数,来确定脉冲响应函数。
河南科技大学机
电工程学院
过程控制系统建模方法
X(t)
线性对象脉冲 响应函数g(t)
Y(t)
对象输入—输出关系示意图
河南科技大学机电工程学院
过程控制系统建模方法
相关分析法求对象脉冲响应函数的方框图
河南科技大学机电工程学院
过程控制系统建模方法
该方法有两个困难: 一是要获得精确的互相关函数,就必 须在较长一段时间内进行积分。这样会产生信号 漂移等其它问题。 二是白噪声是一种数学上的描述,在 物理上无法实现。为解决这两个困难,常用的办 法是采用伪随机信号作为输入探测信号。
河南科技大学机电工程学院
过程控制系统建模方法
4 、用 M 序列作为测试信号来辨识对象的脉冲响 应函数的步骤, 步骤大致如下:
河南科技大学机电工程学院
过程控制系统建模方法
(1)通过预备实验粗估对象的特性 (2)选择M序列的参数 (3)选择测试信号的幅值a (4)用伪随机信号发生器或计算机产生M序 列伪随机信号,施加于被测系统。 (5)输入信号的同时记录输入、输出的数据。 (6)计算互相关函数,并采用前述实验结果的 数据处理办法求传递函数。
河南科技大学机电工程学院
过程控制系统建模方法 用M序列辩识对象的实例 某常压加热炉,炉膛温度受所加燃料的影响, 燃料量又与燃料调节阀的压力有关,现在要求 测定燃料压力与炉膛温度之间的动态关系。
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法
河南科技大学机电工程学院
过程控制系统建模方法
可求得过程的传递函数如下:
87 ?3.32 S G(S ) ? e 44.09 S 2 ? 13.28 S ? 1
河南科技大学机电工程学院
过程控制系统建模方法
互相关函数
河南科技大学机电工程学院
过程控制系统建模方法
过程的阶跃响应曲线
河南科技大学机电工程学院
过程控制系统建模方法
2.3.4 最小二乘法
最小二乘的基本思想“未知量的最可能的 值,它使各次实际观测值和计算值之间的差值 和为最小”。
河南科技大学机电工程学院
过程控制系统建模方法
设y是一根金属轴的长度,T是金属轴 的温度,求轴长y和温度T之间的关系。 第一步 : 确定 y 和 T 之间关系的数学模 型的类型和结构。 第二步:确定变量之间函数关系中的未 知参数。
河南科技大学机电工程学院
过程控制系统建模方法 y和T之间是线性关系。 y = y0(1 + αT) = a + bT y0——0℃时金属轴的长度; α----膨胀系数。
河南科技大学机电工程学院
过程控制系统建模方法
在加噪声干扰下,写成 Zi= Yi(真值)+ ni(随机误差) 即Zi= a + bTi+ ni i = 1,2,…,N
河南科技大学机电工程
学院
过程控制系统建模方法
根据N次(> 2)观测数据(Ti Zi)来估计 出未知参数a和b的值。
河南科技大学机电工程学院
过程控制系统建模方法 a 和 b 的值确定能使观测值和模型的 计算值之间误差为最小。每次观测误差为 ni= zi - yi= zi- (a + b) 相加起来的误差为
?n
i ?1
N
i
? n1 ? n2 ? ? ? n N
河南科技大学机电工程学院
过程控制系统建模方法
常用误差平方和作为总误差。即
J ? ? ni ? ?[ z i ? (a ? bTi )]
2 i ?1 i ?1
N
N
2
河南科技大学机电工程学院
过程控制系统建模方法
按照求极值的原理,要使J最小,只 要将J分别对a和b 求偏导数,令其等于零,a和b ? ? 的估计值 a 和 b 满足下面的条件:
河南科技大学机电工程学院
过程控制系统建模方法
N ? ?J ? ?2? ( z i ? a ? bTi ) ? 0 ? ? ?a i ?1 ? ?J N ? ? ?2? ( z i ? a ? bTi )Ti ? 0 ? i ?1 ? ?b
? 即a
? 和 b 由下列方程组所确定
N ? N ? ? b ? Ti ? aN ? ? z i ? ? i ?1 i ?1 ?? N N N ? 2 ?b ? Ti ? a ? Ti ? ? z i Ti ? i ?1 i ?1 ? i ?1
(2-78)
河南科技大学机电工程学院
过程控制系统建模方法 由式(2-78)可解出
N N N N ? 2 T ? ? ? i ? z i ? ? Ti ? Ti z i i ?1 i ?1 i ?1 ?a ? i ?1 N N 2 ? 2 N T ? ( T ) ? ? i i ? ? i ?1 i ?1 ? N N N ? N ? Ti z i ?? Ti ? z i ? ? i ?1 i ?1 i ?1 b ? N N ? 2 ? N ? Ti ? (? Ti ) 2 ? i ?1 i ?1 ?
(2-79)
河南科技大学机电工程学院
过程控制系统建模方法
假定一个变量y与一组n维变量X=(x1,x2--xn)有线性关系。即 y = ? x ? ? x ? ?? ? x (2-80)
1 1 2 2 n n
河南科技大学机电工程学院
过程控制系统建模方法
N个参数的线性系统
河南科技大学机电工程学院
过程控制系统建模方法
假设用 y(i)和x1(i)、x2(i)---xn(i),i =1,2,..,m 表示 实测数据。可以通过m个线性方程的方程组表示数 据之间的关系。
y(i) ? ?1 x1 (i) ? ? 2 x2 (i) ? ? ? ? n xn (i)
i =1,2,..,m 回归函数,? i 是回归系数。
河南科技大学机电工程学院
过程控制系统建模方法
可以用矩阵形式表示如下
Y ? X?
(2-82)
河南科技大学机电工程学院
过程控制系统建模方法
? y (1) ? ? y ( 2) ? ? Y ?? ? ? ? ? ? ? y ( m) ?
? x1 (1) ? x n (1) ? ? x (2) ? x (2) ? 1 n ? ? X ? ???????? ? ? ? x1 (m) ? x n (m)?
?? 1 ? ?? ? 2? ? ? ? ??? ? ? ?? n ?
河南科技大学机电工程学院
过程控制系统建模方法 若m=n,根据方程通过下式求解
(2-83) ?1 X 只要 即方阵 X 的逆存在,则能够唯一地 ? ? ? 的估计值。 ? 求解 ? ,
表示
? ?X Y
?1
?
河南科技大学机电工程学院
过程控制系统建模方法
T ? ( ? , ? ? ? ) 定义误差矢量 且令 1 2 m ? ? Y ? X?
现在以下列性能指标J
? 趋于最小,来选择 ?
J ? ?? i ? ? ?
2 T i ?1
m
。
河南科技大学机电工程学院
过程控制系统建模方法
可将式表示成 J ? (Y ? X? )T (Y ? X? ) ? Y T Y ? ? T X T Y ? Y T X? ? ? T X T X? 求J对于 ? 的导数并令结果为零,作为确定 ? 使J为最小的估计值 的条件。 ? 于是 ?
?J ??
? ??
?
? ?2 X T Y ? 2 X T X? ? 0 (2-85)
河南科技大学机电工程学院
过程控制系统建模方法
由此可得
T ? X X? ? X Y T
? T ?1 T ( X X ) X Y ? = ? 称为 ? 的最小二乘估计量(LSE)。
? ? 能按下式求解
方程叫做正规方程,而
? 称为残差。
河南科技大学机电工程学院
过程控制系统建模方法 令W为期望的加权矩阵,则加权误差性能指标 成为
JW ? ? W? ? (Y ? X? ) W (Y ? X? )
T T
河南科技大学机电工程学院
过程控制系统建模方法
W被限制为对称正定矩阵。求Jw对? 的 ? 极小值,可得到加权最小二乘估计量 ? W ? =( X T WX ) ?1 X T WY ? W 容易看出,当W选择为一个单位矩阵I时, ? ? ?W 就简化为 ? 。
河南科技大学机电工程学院
过程控制系统建模方法
本章小结
建模的原理一般可分为机理法和测试法。 1、机理法建模就是根据所研究系统各部件的生产 过程中实际发生的变化机理,写出多种有关的平衡 方程,分析过程的内在联系,消去中间变量,写出 输入与输出变量之间的关系。
河南科技大学机电工程学院
过程控制系统建模方法
2、单容对象指只有一个储能部件的对象, 是由一阶传递函数所描述。该单容对象 有、无平衡能力可分别用一阶惯性环节 或积分环节来描述。对于有些对象中某 些变量不能瞬时跟踪变化,需要一定的 ?0 延时 ,因而在数学模型中以纯延时环 ?? s e 节 来表示。
0
河南科技大学机电工程学院
过程控制系统建模方法 3 、多容对象是指有多个储能部件的对象,它对 应的数学模型是高阶传递函数。 4 、测试法建模,它是根据过程的输入和输出的 实测数据进行某种数学处理后得到的模型。 它完全从外特性上测试和描述它的动态性质,可 以不要求掌握其内部机理。采用测试法时注意输入 信号的选择和测试数据的准确性。
河南科技大学机电工程学院
过程控制系统建模方法 5、测定动态特性的时域方法。 根据对被控对象施加阶跃输入,测绘出对象 输出量随时间变化的响应曲线, 或施加脉冲输入测绘出输出的脉冲响应曲线。 由响应曲线的结
果分析,确定出被控对象的传递 函数。
河南科技大学机电工程学院
过程控制系统建模方法
使用这种方法可首先确定被测系统的模 型阶次,选择合适的标准模型类型,然后采取一种 方法确定出参数。
河南科技大学机电工程学院
过程控制系统建模方法
6、测定动态特性的频域方法,根据BOD图的原 理,对被控对象施加不同频率的正弦波,测出输 入量与输出量的幅值比和相位差,从而获得对象 的频率特性,来确定被控对象的传递函数。
河南科技大学机电工程学院
过程控制系统建模方法
7、测定动态特性的统计相关法。 对被控对象施加某种随机信号或直接利用 对象输入端本身存在的随机噪音进行观察和记录, 可以在生产过程正常运行状态下进行在线辨识, 精度较高。
河南科技大学机电工程学院
过程控制系统建模方法
8、测定动态特性的辨识方法。 必须假定一种模型结构,通过极小化模型与 过程之间的误差准则函数来确定模型的参数。 这类辨识方法根据不同的基本原理又可分为最小 二乘法;梯度校正法;极大似然法三种类型。
河南科技大学机电工程学院
三 : 建模方法
数学建模方法
第一届研究生数学建模竞赛赛题 方法总结
A 发现黄球并定位 —图论(着色问题)、 调度问题 B 实用下料问题 —多目标整数规划、整数 线性规划 C 售后服务数据的运用 —最小二乘拟合、 时间序列、滤波方法 D 研究生录取问题 —(模糊)层次分析、 0-1整数规划、对策论、图的匹配问题
数学建模需要的知识
? 运筹学 ? 多元统计分析
? 微分方程
数学建模常用的方法
类比法 ? 量纲分析法 ? 差分法 ? 变分法 ? 图论法 ? 层次分析法 ? 数据拟合法 ? 回归分析法 ? 数学规划(线性规划,非线性规划,整数规 划,动态规划,目标规划)
?
数学建模常用的方法
机理分析法 ? 排队方法 ? 对策方法 ? 决策方法 ? 模糊评判方法 ? 时间序列方法 ? 灰色理论方法 ? 现代优化算法(禁忌搜索算法,模拟退火 算法,遗传算法,神经网络)
?
数学模型分类
? 优化模型 ? 微分方程模型
? 统计模型
? 概率模型 ? 图论模型 ? 决策模型
拟合与插值方法
? 问题—给定一批数据点(输入变量与输
出变量的数据),需确定满足特定要求 的曲线或曲面 ? 插值问题—要求所求曲线(面)通过所 给所有数据点 ? 数据拟合—不要求曲线(面)通过所有 数据点,而是要求它反映对象整体的变 化趋势
数据拟合
? 一元函数拟合
? 多项式拟合
? 非线性函数拟合
? 多元函数拟合(回归分析) ? MATLAB实现 ? 函数的确定
插值方法
? 一维插值的定义—已知n个节点,求任意
点处的函数值。
? 分段线性插值 ? 多项式插值 ? 样条插值
? y=interp1(x0,y0,x,'method')
? 二维插值—节点为网格节点
? z=interp2(x0,y0,z0,x,y,'method') ? pp=csape({x0,y0},z0,conds,valconds)
? 二维插值—节点为散点
? z1=griddata(x,y,z,x1,y1)
优化方法
? 优化模型四要素
? 决策变量
? 目标函数(尽量简单、光滑) ? 约束条件(建模的关键)
? 求解方法 (MATLAB,LINDO)
优化模型分类
? ? ?
?
?
?
线性规划模型(目标函数和约束条件都是线性 函数的优化问题) 非线性规划模型(目标函数或者约束条件是非 线性的函数) 整数规划(决策变量是整数值得规划问题) 多目标规划(具有多个目标函数的规划问题) 目标规划(具有不同优先级的目标和偏差的规 划问题) 动态规划(求解多阶段决策问题的最优化方法)
优化模型求解
?
无约束规划
? fminsearch ? fminbnd
?
线性规划
? linprog
?
? ?
非线性规划
? fmincon
多目标规划(计算有效解)
? 目标加权、效用函数
动态规划(倒向、正向) ? 整数规划(分支定界法、枚举法、LINDO)
统计方法(
回归分析)
?
?
回归分析—对具有相关关系的现象,根据其关系形态, 选择一个合适的数学模型,用来近似地表示变量间的 平均变化关系的一种统计方法 (一元线性回归、多 元线性回归、非线性回归) 回归分析在一组数据的基础上研究这样几个问题:
? ? ? ? ?
建立因变量与自变量之间的回归模型(经验公式) 对回归模型的可信度进行检验 判断每个自变量对因变量的影响是否显著 判断回归模型是否适合这组数据 利用回归模型对进行预报或控制
? ? ?
[b, bint,r,rint,stats]=regress(Y,X,alpha) (线性回归) rstool(x,y,’model’, alpha)(多元二项式回归) [beta,r,J]=nlinfit(x,y,’model’, beta0)(非线性回 归)
统计方法(逐步回归分析)
?
逐步回归分析—从一个自变量开始,视自变量 作用的显著程度,从大到地依次逐个引入回归 方程
? 当引入的自变量由于后面变量的引入而变得不显著
时,要将其剔除掉 ? 引入一个自变量或从回归方程中剔除一个自变量, 为逐步回归的一步 ? 对于每一步都要进行值检验,以确保每次引入新的 显著性变量前回归方程中只包含对作用显著的变量 ? 这个过程反复进行,直至既无不显著的变量从回归 方程中剔除,又无显著变量可引入回归方程时为止
?
stepwise(x,y,inmodel,alpha) ? SPSS,SAS
统计方法(聚类分析)
? 聚类分析—所研究的样本或者变量之间存
在程度不同的相似性,要求设法找出一些 能够度量它们之间相似程度的统计量作为 分类的依据,再利用这些量将样本或者变 量进行分类 ? 系统聚类分析—将n个样本或者n个指标看 成n类,一类包括一个样本或者指标,然 后将性质最接近的两类合并成为一个新类, 依此类推。最终可以按照需要来决定分多 少类,每类有多少样本(指标)
统计方法(系统聚类分析步骤)
系统聚类方法步骤: 1. 计算n个样本两两之间的距离 2. 构成n个类,每类只包含一个样品 3. 合并距离最近的两类为一个新类 4. 计算新类与当前各类的距离(新类与当 前类的距离等于当前类与组合类中包含 的类的距离最小值),若类的个数等于 1,转5,否则转3 5. 画聚类图 6. 决定类的个数和类。
统计方法(判别分析)
判别分析—在已知研究对象分成若干类型,并已取 得各种类型的一批已知样品的观测数据,在此基础 上根据某些准则建立判别式,然后对未知类型的样 品进行判别分类。 ? 距离判别法—首先根据已知分类的数据,分别计算 各类的重心,计算新个体到每类的距离,确定最短 的距离(欧氏距离、马氏距离) ? Fisher判别法—利用已知类别个体的指标构造判别 式
(同类差别较小、不同类差别较大),按照判别 式的值判断新个体的类别 ? Bayes判别法—计算新给样品属于各总体的条件概率, 比较概率的大小,然后将新样品判归为来自概率最 大的总体
?
与模糊数学相关的问题(一)
? 模糊数学—研究和处理模糊性现象的数
学 (概念与其对立面之间没有一条明确 的分界线) ? 与模糊数学相关的问题(一)
? 模糊分类问题—已知若干个相互之间不分明
的模糊概念,需要判断某个确定事物用哪一 个模糊概念来反映更合理准确 ? 模糊相似选择 —按某种性质对一组事物或对 象排序是一类常见的问题,但是用来比较的 性质具有边界不分明的模糊性
与模糊数学相关的问题(二)
? 模糊聚类分析—根据研究对象本身的属性构
造模糊矩阵,在此基础上根据一定的隶属度 来确定其分类关系 ? 模糊层次分析法—两两比较指标的确定 ? 模糊综合评判—综合评判就是对受到多个因 素制约的事物或对象作出一个总的评价,如 产品质量评定、科技成果鉴定、某种作物种 植适应性的评价等,都属于综合评判问题。 由于从多方面对事物进行评价难免带有模糊 性和主观性,采用模糊数学的方法进行综合 评判将使结果尽量客观从而取得更好的实际 效果
时间序列分析建模
时间序列是按时间顺序排列的、随时间变化且 相互关联的数据序列—通过对预测目标自身时 间序列的处理,来研究其变化趋势(长期趋势 变动、季节变动、循环变动、不规则变动) ? 自回归模型
?
? 一般自回归模型AR(n)—系统在时刻t的响应X(t)仅与
其以前时刻的响应X(t-1),…, X(t-n)有关,而与其以 前时刻进入系统的扰动无关 ? 移动平均模型MA(m)—系统在时刻t的响应X(t) ,与 其以前任何时刻的响应无关,而与其以前时刻进入 系统的扰动a(t-1),…,a(t-m)存在着一定的相关关系 ? 自回归移动平均模型 ARMA(n,m)—系统在时刻t的响 应X(t),不仅与其前n个时刻的自身值有关,而且还 与其前m个时刻进入系统的扰动存在一定的依存关 系
时间序列建模的基本步骤 (1)
1. 数据的预处理:数据的剔取及提取趋势项 2. 取n=1,拟合ARMA(2n,2n-1)(即ARMA(2,1))
模型
3. n=n+1,拟合ARMA(2n,2n-1)模型
4. 用F准则检验模型的适用性。若检验显著,则
转入第2步。若检验不显著,转入第5步。 5. 检查远端时刻的系数值的值是否很小,其置 信区间是否包含零。若不是,则适用的模型 就是ARMA(2n,2n-1) 。若很小,且其置信区 间包含零,则拟合ARMA(2n-1,2n-2) 。
时间序列建模的基本步骤 (2)
6.
7.
8.
利用F准则检验模型ARMA(2n,2n-1)和 ARMA(2n-1,2n-2) ,若F值不显著,转 入第7步;若F
值显著,转入第8步。 舍弃小的MA参数,拟合m<2n-2的模型 ARMA(2n-1,m) ,并用F准则进行检验。 重复这一过程,直到得出具有最小参数 的适用模型为止 舍弃小的MA参数,拟合m<2n-1的模型 ARMA(2n,m) ,并用F准则进行检验。重 复这一过程,直到得出具有最小参数的 适用模型为止。
图论方法(一)
?
最短路问题
? 两个指定顶点之间的最短路径—给出了一个连接若干
个城镇的铁路网络,在这个网络的两个指定城镇间, 找一条最短铁路线 (Dijkstra算法 ) ? 每对顶点之间的最短路径 (Dijkstra算法、Floyd算法 )
?
最小生成树问题
? 连线问题—欲修筑连接多个城市的铁路设计一个线路
图,使总造价最低(prim算法、Kruskal算法 )
?
图的匹配问题
? 人员分派问题:n个工作人员去做件n份工作,每人适
合做其中一件或几件,问能否每人都有一份适合的工 作?如果不能,最多几人可以有适合的工作?(匈牙利 算法)
图论方法(二)
? 遍历性问题
? 中国邮递员问题—邮递员发送邮件时,要从
邮局出发,经过他投递范围内的每条街道至 少一次,然后返回邮局,但邮递员希望选择 一条行程最短的路线
? 最大流问题
? 运输问题
? 最小费用最大流问题
? 在运输问题中,人们总是希望在完成运输任
务的同时,寻求一个使总的运输费用最小的 运输方案
竞赛中的群体思维方法
? 平等地位、相互尊重、充分交流 ? 杜绝武断评价
? 不要回避责任
? 不要对交流失去信心
竞赛中的发散性思维方法
?
借助于一系列问题来展开思路
? 这个问题与什么问题相似? ? 如果将问题分解成两个或几个部分会怎样? ? 极限情形(或理想状态)如何? ? 综合问题的条件可得到什么结果? ? 要实现问题的目标需要什么条件?
?
借助于下意识的联想(灵感)来展开思路
? 抓住问题的个别条件或关键词展开联想或猜想 ? 综合所得到的联想和猜想,得到一些结论 ? 进一步思考找出新思路和方法
对赛题的把握和理解问题
? 认真仔细地识题 ? 明确条件和任务
? 通过关键词捕捉关键信息
? 分清是非,勿入陷井
祝大家在竞赛中取 得好成绩!
四 : 建模方法
就常用的建模方法而言,基本上可以分为基于运筹学的建模方法(ORbased Modeling Methods)、基于控制论的方法(Control theorists basedModeling Methods)、基于系统仿真的建模方法(Simulation basedModeling Methods),基于企业建模方法的研究方法(Enterprise modelbased Modeling Methods)。61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1